山地复杂构造区叠前深度偏移初始层速度约束反演改进新方法
2022-06-07熊晶璇贺振华赵容容杨卫宁张恩嘉王光银
熊晶璇 贺振华 刘 鸿 赵容容 杨卫宁 张恩嘉 王光银 唐 虎
1.成都理工大学 2.中国石油天然气集团公司东方地球物理勘探有限公司3.中国石油天然气集团公司山地地震技术试验基地 4.中国石油西南油气田公司勘探事业部
0 引言
前陆盆地发育在稳定克拉通与线性收缩造山带的结合部位,有着鲜明的构造—沉积特征,油气成藏条件优越[1-4]。众多学者论述了前陆盆地是重要的含油气单元[5-8]。近年来,塔西南、准噶尔南缘,川西南等前陆盆地油气勘探取得重要进展[9-13],也证实了该领域巨大的勘探潜力。前陆盆地油气资源丰富,但其地下构造复杂,多存在高陡构造上下盘展布差异大,断裂发育,地层倾角变化大,构造倒转[1-2,6-7],目标地质体埋藏深、尺度小等现象[14-17],在速度模型上表现为速度纵横向变化大,普遍存在速度倒转和局部高频等现象、山地复杂构造的深度域速度模型建立和更新等问题成为业界难题[17]。因此,针对性研究适合复杂山地油气勘探的深度域速度建模技术具有重要意义。
初始层速度模型建立是深度域速度建模的第一步。在山地复杂构造区域,因地下地质情况复杂造成速度场复杂,使深度域速度模型的迭代更新更依赖于初始层速度模型[18],高质量的初始层速度模型既可加快速度更新的收敛,又能进一步提高偏移成像的效果和效率。经典Dix反演是常用的初始层速度模型建立方法,它建立在水平层状或小倾角地层与速度横向无变化假设的理论基础上[19],但山地复杂构造时距曲线方程多为非双曲线型,经典Dix反演抗干扰能力弱,提供的层速度变得不可靠[20]。为了获得可靠的层速度,Hubral等学者对经典Dix公式进行了研究[21-23],Clapp等学者针对Dix 公式假设[24-25],提出了改进的约束Dix反演层速度的求取方法。Koren 和Ravve提出了约束层速度反演 CVI 方法[26],进一步提高速度模型的横向连续性[27-29]。但如前所述,山地复杂构造区速度场复杂,CVI方法作为常用方法,通过单一固定的影响域对所有局部构造进行约束,反演结果精确性的风险,甚至会引入局部误差, 并在反演中将误差传递放大,影响结果的正确性。除此之外,常规算法中对速度的离散数据进行网格化时,多基于速度体横向变化平缓,在山地复杂地质区,因存在构造倒转和局部异常地质体带来的速度倒转和局部速度高频等现象,常规的插值平滑方法会降低速度模型对倒转构造和小规模地质体的灵敏性,增加速度更新迭代收敛的次数,甚至会带来速度模型的扭曲,影响叠前深度偏移的成像质量。
本文通过形成构造约束的速度趋势函数和基于径向基函数薄板理论的三维空间速度网格重构函数,在常规约束速度反演研究的基础上,形成了山地复杂构造区初始层速度改进反演方法,该方法在复杂构造区域反演得到的层速度场更符合地质规律,反演效果优于常规方法。该方法研究成果有助于推进我国复杂构造区油气勘探开发。
1 方法原理
常规约束速度反演方法的目标函数由均方根速度拟合、指数渐进边界速度趋势函数拟合(以下简称趋势函数拟合)和防振荡阻尼拟合三部分组成[26,30]。其中,均方根速度拟合是均方根速度对反演结果的贡献。防振荡阻尼拟合用来压制界面上下纵向速度梯度的过大跳跃。速度趋势函数拟合用于改善Dix反演带来的高频振荡,影响甚至决定了反演结果的合理性和稳定性。Ravve[31]等提出两个粗网格点间用指数形式的趋势速度填充,对改善经典Dix反演时出现的高频振荡,具有重要的贡献意义。速度趋势函数即指数渐进边界速度趋势函数(Exponential, Asymptotically Bounded Model,简称 EAB 函数),其数学表达式为[31-33]:

Ravve[31]等进一步提出一定影响半径内的粗网格上所有的垂直函数都相互影响,影响权重与距离成反比。影响域具有一定的全局性,在构造平缓区域,反距离加权的影响权重也具有统计学意义,可以较好地解决速度反演的横向连续性问题。影响权重和半径的数学表达为[31-33]:
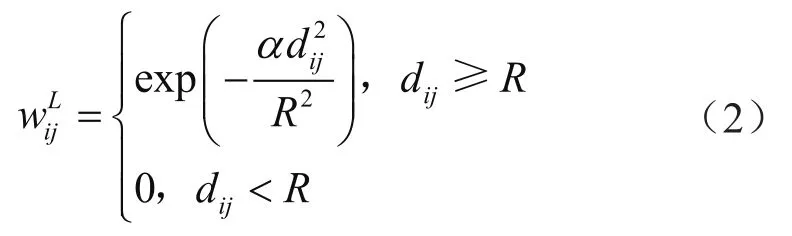
式中R表示影响域的半径,m;dij表示两道的距离,m;i表示RMS垂直函数的序号;j表示速度趋势函数的序号;表示某给定的值,ξ表示预设的极小值,一般为10-2。
加入影响半径和权重后趋势函数变为[32-33]:
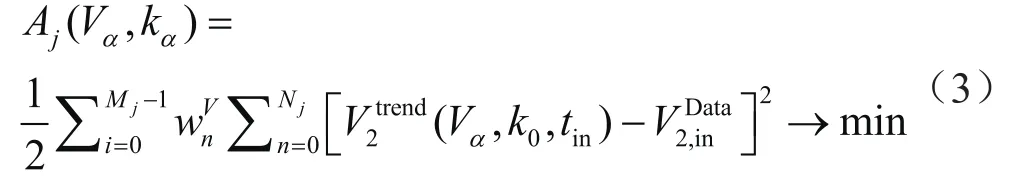
式中,内层求和表示对第i个垂直速度函数的所有Ni+1个纵向网格点的累加,外层求和表示横向网格点i为中心影响半径内的全部Mj个垂直速度函数的累加。wVn表示影响半径内各道对中心点的影响权重系数。
1.1 构造约束的趋势函数
由式(2)、(3)可知,影响半径和权重是保证EAB 函数计算稳定性和合理性的重要因子。在构造平缓区域,速度模型横向变化平缓,固定影响半径的引入能提高计算稳定性,使单道反演扩展为半径范围内的多点信息联合反演,起到很好的约束效果。但在构造复杂区域,保证速度横向连续的基础上,要剔除异常高频振荡,还要保留地质体引起的速度突变和倒转,单个固定的影响半径存在较大局限性,使用大尺度影响半径满足平缓构造剔除速度异常的需求,在构造变化位置速度模型的精度受损;采用小尺度影响半径保证构造部位的速度精度,平缓构造的速度异常未被有效剔除,并且在构造复杂区域,采用反距离加权函数作为影响权重,很可能为当前分析点引入较大误差,以上问题均会影响成像效果,如图1所示。

图1 使用不同影响半径反演的速度模型的单道速度曲线和偏移成像道集图
经过研究,利用时间偏移剖面的道间相关系数,反映地质构造的横向连续和变化特征,在反演方程中自动形成影响半径,使用自动形成的不同影响半径匹配不同局部构造的规模和形态进行反演约束,即构造约束的速度趋势函数,能提高速度约束反演精度[34-35],尽可能降低横向速度振荡,并提高层速度场对小规模地质体的响应。求取道间相关系数的方法很多,如归一化互相算法、基于几何结构张量的相关算法、多属性复相关算法等。在山地复杂地质构造区域,资料信噪比常不理想,过于简单的相关算法很难达到理想效果,过于复杂的算法在硬件成本、人力成本和时间成本上很难满足生产需求,并且资料信噪比低易导致求解困难。因此,通过对比研究,选择对多道互相关算法进行改进,分析道采用模型道替代,根据目的层形成时窗,在时窗内进行相关系数的计算并取最优系数,保证相关系数计算的稳定性,公式为 :
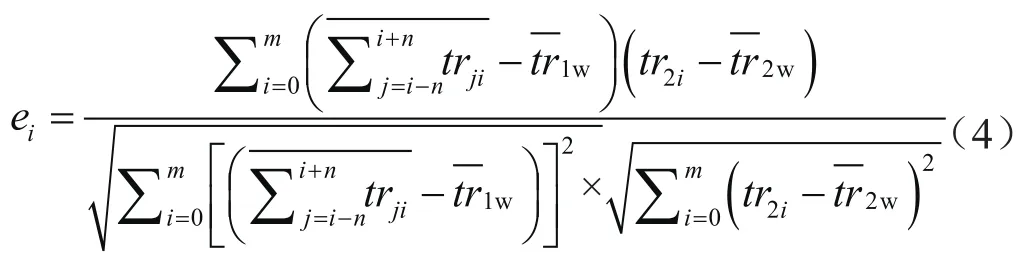
式中ei表示两地震道的相关系数,无量纲;trji表示构建当前道的模型道的地震道数据;tr2i表示除当前道的其他地震道数据;表示时窗内的地震道数据的平均值;m表示时窗内的纵向样点数,n表示纳入模型道计算的地震道数。
由前面分析可知,当ei大于预设的接受系数,说明道间相关系数大,地震道地质特征相似,可累加该处速度信息进行反演,此时影响半径为纳入模型道计算的道数的累加。因此,构造约束的速度趋势函数的目标方程可写为:

式(5)是一个最优化问题,牛顿法和拟牛顿法是求解最优化问题最常用的数值方法,由于在计算中不需要精确地计算Hessian矩阵,又因L-BFGS(Limited-memory BFGS)算法内存占用少,计算复杂度低,稳定性较好,所以本文一并使用L-BFGS算法来求解最优值。
1.2 保持构造信息的速度体重构算法
上述计算是在给定空间拾取点上沿着时间方向离散进行的,数据离散化可以减少计算成本、提高计算速度,并且简化逻辑,降低模型过拟合的风险,同时离散化后的特征对异常数据也有很强的鲁棒性。但初始层速度反演,最终还是要面临将离散的速度样点重建为速度体,以供后续速度更新和偏移成像步骤使用的问题。常规方法对此讨论不多,常使用普通的插值和平滑函数解决此问题,但无论是一维还是多维插值平滑多基于水平和垂直方向。在构造平缓区域普通的插值和平滑函数不仅能降低反演求解的多解性,保证反演算法的稳定,还能剔除速度模型的异常。但在构造复杂区域,特别是大倾角构造区域和局部小规模异常地质体区域,常规插值平滑不仅会模糊掉小尺度地质体和构造倒转处的速度响应信息,甚至会带来速度模型的扭曲。并且,在山地复杂构造区域因资料信噪比等原因,速度拾取点的空间展布并不一定是均匀给出,这对速度模型网格连续化带来更大挑战。利用径向基函数薄板理论形成保持构造信息的三维空间速度体重构算法可有效解决此问题。
径向基函数具有形式简单,对支撑域和边界无过多要求,仅需以分析点为中心的子域并集覆盖整体域就能得到精确结果。保持构造信息的速度体重构算法将分布在空间上的节点构造径向基函数, 将具有相同时间的层速度在物理模型上类似地形成一个带有自由边界的平面薄板,在此平面薄板上的速度信息重构可以看作是下面问题s(x,y) 的求解。


薄板样条(TPS)函数[36]是离散数据插值方法中插值精度非常高的方法[37-38]。Duchon从约束优化的角度出发,以泛函的观点提出薄板样条(Thin-plate spline)理论,由其满足插值条件,并取弯曲能最小的结论可知[38],满足这一问题的s(x,y)具有下面的形式 :

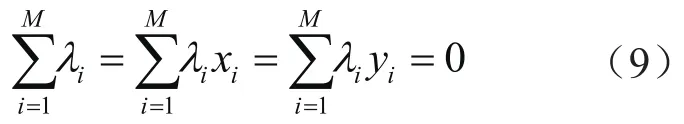
结合式(7)、(8),并做下面记号,可以得到与式(7)、(8)等价的方程组(10):

其中:
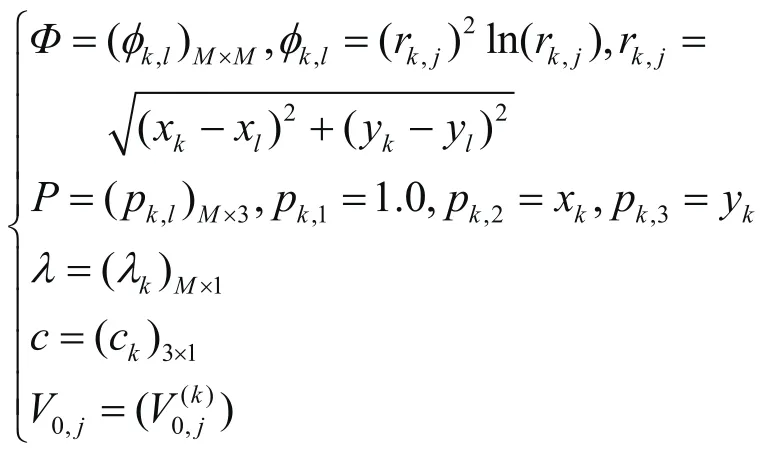
图2给出了一个单层保持构造信息的速度体重构算法例子,图 2-a 给出了空间离散节点的分布及约束条件,插值节点数为 1 466 个,空间分布非均匀,约束条件的变化趋势梯度较大。图2-b、c显示了插值结果及与插值条件的叠合比较,从图2-b、c中可以看出插值结果很好地反映了插值条件的变化趋势,速度模型与插值条件吻合,同时符合地质规律的变化,结果合理平滑精细,这正是后续深度域速度层析反演所需要的。

图2 构造约束的空间三维体插值平滑图
1.3 复杂构造约束层速度反演方法
山地复杂构造区的约束层速度反演改进算法从算法分解来看,求解公式(5)得到各网格点的趋势速度,将其带入指数渐进趋势函数公式中[31-33]:

形成构造约束的速度趋势函数拟合:
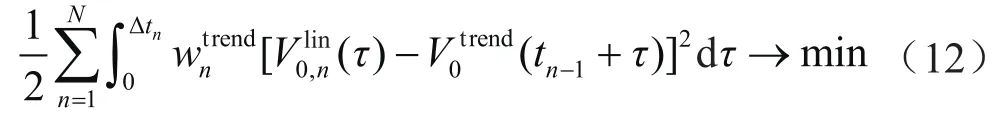
2 理论模型应用效果
采用合成理论模型对本文提出的初始层速度改进反演方法(以下简称本文方法)进行应用。
理论模型模拟速度倒转情况纵向长度为1 s,横向长度为1 200 m,共设置了四层速度,第一层速度值为1 500 m/s,第二层速度值为3 100 m/s,第三层速度为2 000 m/s,第四层速度为4 000 m/s,其中第二层速度和第三层速度发生倒转,为重点测试本文形成的自适应速度趋势拟合算法和保持构造信息的速度体重构算法的稳定性,在此测试中采用小阻尼权,减少影响。
图3-a~d对比可知,本文方法使用了多种参数都能较好的还原理论模型,模型的形态和速度都吻合较好,特别是在速度倒转时表现了较好的稳定性,速度倒转层不仅速度误差小而且未出现任何异常高频,从图3-e单道曲线可知,速度模型的形态、速度和深度非常接近真实模型,在速度倒转处最大误差小于3%,除去速度转换、正则化、网格化、反演迭代平滑等精度损失,本文方法很好地还原了真实模型,证明方法的正确性和较高精度。

图3 理论模型一和不同参数的反演速度模型图
理论模型二模拟了山地复杂地质情况,不仅存在地层尖灭,还存在小尺度局部地质体。在速度模型上表现为横向速度突变、速度倒转和局部高频速度团,这是速度反演的大挑战。模型纵向长度为1 s,横向长度为1 200 m,共设置了六层速度,分别是1 500 m/s、1 800 m/s、2 000 m/s、2 800 m/s、3 200 m/s、4 000 m/s,在第二层设置了地层尖灭引起的横向速度突变,在第三层设置了小尺度地质体引起的速度倒转,第四层设置了小尺度地质体引起的局部速度高频。采用了不同的参数测试本文方法在复杂地质环境下的可靠性和稳定性。
由图 4-a ~ c 对比可知,对于复杂地质速度环境,本文方法能很好地还原理论模型,从模型的形态、速度、深度均能与理论模型较好吻合,特别是在地层尖灭和小目标地质体的速度反演上表现出较高的稳定性。仅从此理论模型看,本文基于构造的速度趋势函数算法与三维复相关自适应算法[35]的效果类似。从反演速度模型的单道曲线也可以看出除去速度转换、正则化、网格化、反演迭代平滑等带来的精度损失,速度曲线的形态、速度和深度非常接近真实模型,证明本方法的正确性和在复杂地质和速度条件下的较高精度。

图4 理论模型二和不同参数的反演速度模型和单道速度曲线图
3 实际数据的应用效果
为进一步验证本文方法在实际地震数据上的反演效果,将本方法应用于深丘地区弧形褶皱带交汇处复杂构造区的地震资料处理上,并通过反演速度模型和偏移成像效果与常规速度约束反演方法进行对比。实际资料剖面长度16 km,纵向长度8.0 s,给定初始的均方根速度场空间分析点共32道,反演得到的速度模型网格重建为大小650 m×1 250 m。由于实际资料的信噪比不高,为保证叠前深度偏移效果,常规方法选择1 km的固定影响半径。采用两种方法反演得到的初始深度域层速度模型见图5。
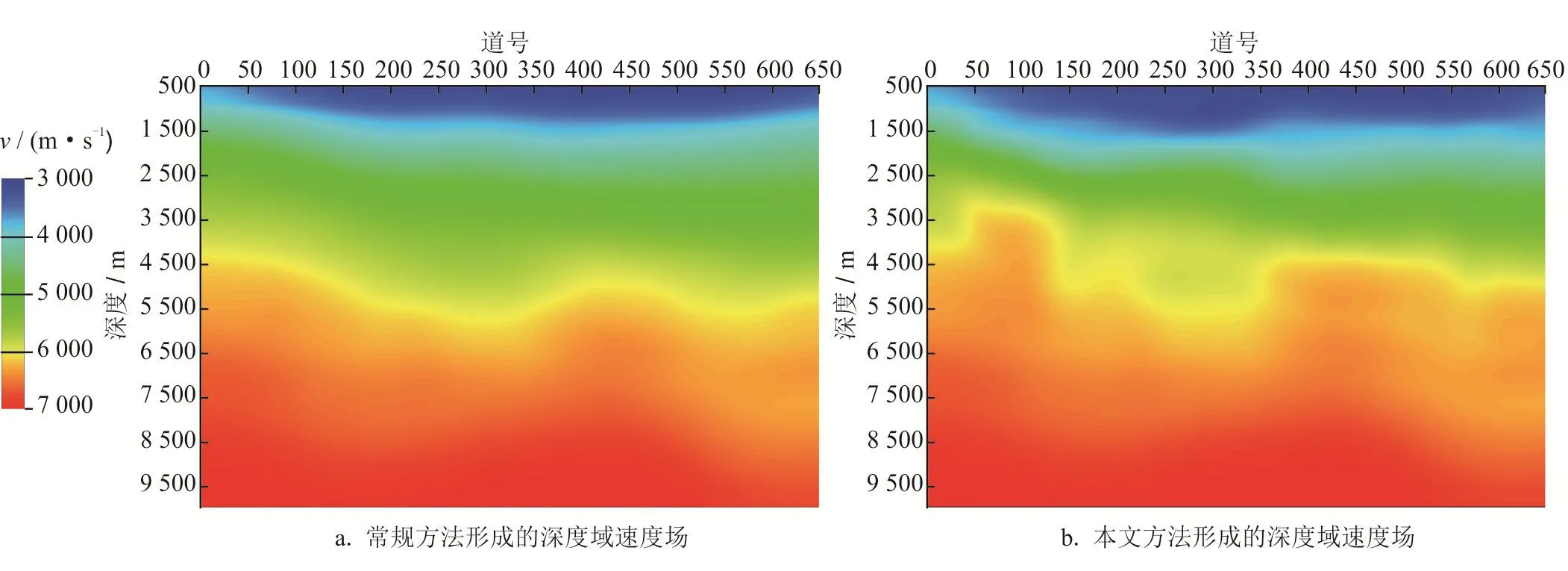
图5 反演得到的初始层速度模型图
图5可知,常规方法采用了较大尺度平滑,但地质信息也被模糊掉。采用本文方法得到的速度模型较好地保留了地质信息,模型速度变化趋势与地质认识一致。
山地构造复杂区,地层倾角陡,地层速度变化大,如果速度模型精度不高很容易导致构造翼部成像不准或者在逆掩构造顶部成像效果差,甚至不成像。叠前深度偏移成像质量是检验速度模型质量的有效手段,将两套速度场利用积分法进行叠前深度偏移,得到偏移成像结果。
从图6、7实际资料的叠前深度偏移结果可知,本文方法形成的速度模型成像效果更佳,共成像点道集在构造部位同相轴更清晰,偏移剖面构造成像不论在构造翼部还是构造顶部成像都更准确,细节更清晰,与地质规律更一致;后续深度域速度更新时也仅需几次迭代更新,就可以完成最终深度域速度模型的建立。
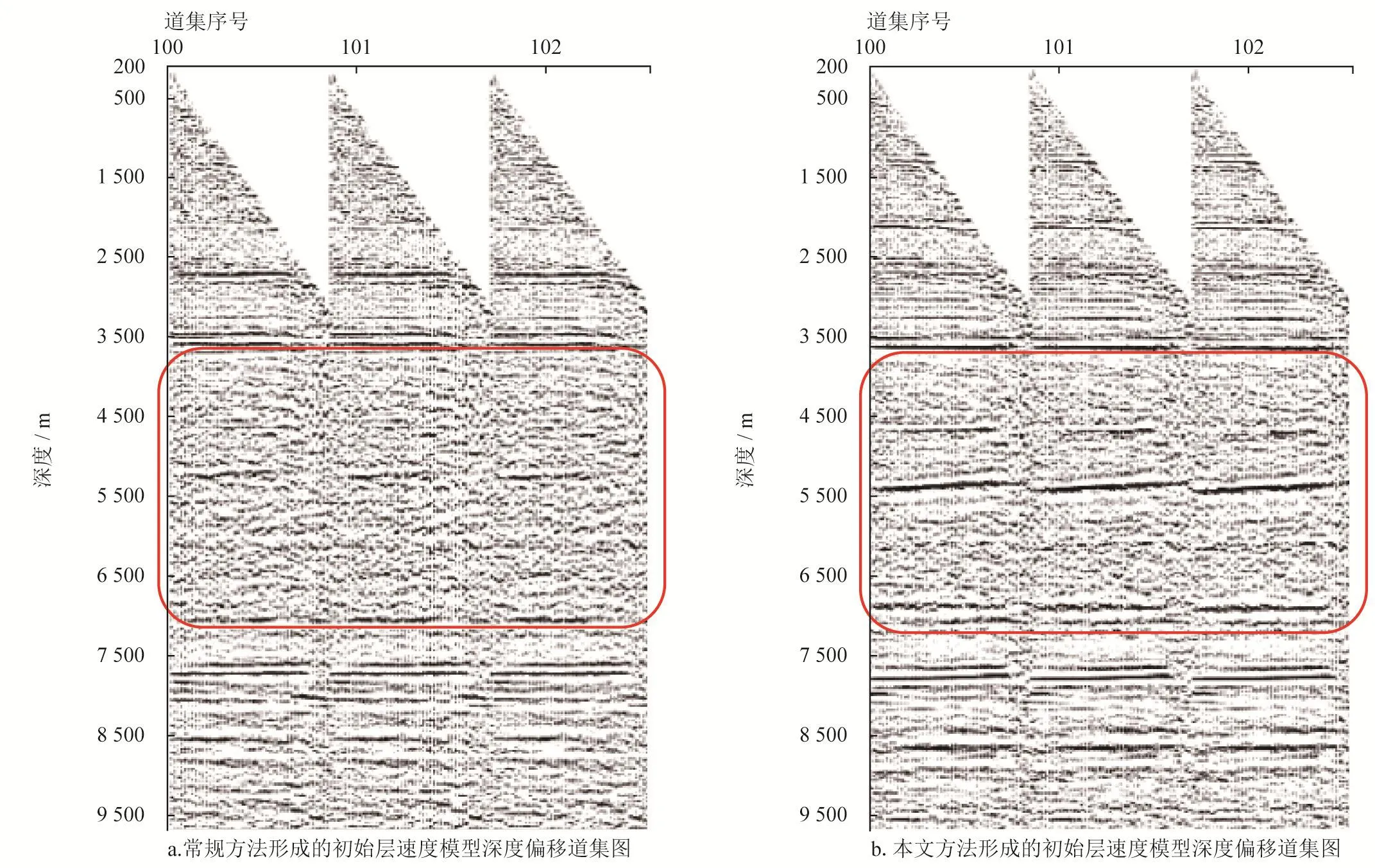
图6 深度偏移部分成像道集对比图

图7 叠前深度深度成像剖面对比图
4 结论
1)本文在对常规约束速度反演方法充分研究的基础上,利用叠前时间偏移剖面上的构造信息使速度趋势函数求解的影响半径和权重随构造特征变化,并利用径向基函数薄板理论形成保持构造信息的三维空间速度体重构算法,最终形成适用于复杂地质区域的初始层速度改进约束反演方程组。
2)在构造复杂区,本文方法在改善速度模型纵横向连续性的同时,更精细地描述地质特征的速度结构,更好保留小规模局部地质体的速度特征。经理论模型测试和实际资料应用,本文方法在山地复杂地质区域有效,且精度较高,得到的层速度模型更有利于深度域速度建模的后续步骤。
3)本文方法中地震数据体道间相关性的计算非常关键,如果资料信噪比极低,相关性的计算精度会受到影响。
