纵连板式无砟轨道动态应变分布规律研究
2022-06-07肖杰灵陈流宇杨荣山刘学毅
胡 颖,肖杰灵,陈 醉,陈流宇,杨荣山,刘学毅
(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031; 2.西南交通大学土木工程学院,成都 610031)
引言
纵连板式轨道是我国高速铁路的主型轨道结构之一,因其整体性好、稳定性高、养护维修工作量小等优势已在我国京津城际、京沪高铁等线路上得到应用[1]。但由于轨道结构线状施工作业、多变的下部基础、列车与温度等环境荷载耦合作用、经时效应下的结构退化等因素作用,运营过程中出现了不同程度的病害,使得其疲劳耐久性问题受到广泛关注。无砟轨道疲劳耐久性作为保证其设计寿命的主要指标,如当前混凝土仅考虑荷载幅值和次数影响的疲劳耐久性检算时,理想状态下无砟轨道一般能满足要求,但在服役过程中会出现层间砂浆破损与离缝,轨道板翘曲变形、宽窄接缝破损及上拱等病害[2],如图1所示。究其原因,在于混凝土材料的特殊性。混凝土材料是典型的率敏感材料,其各项力学性能在动态作用下会产生显著变化[3]。无砟轨道结构作为一种钢筋混凝土组合结构,在列车荷载作用下,层间应变率的变化规律对板式无砟轨道疲劳耐久性研究不容忽视[4]。

图1 砂浆层破损
应变率为衡量单位时间内材料应变量的变化,最早于1917年ABRAMS[5]提出了混凝土应变率敏感性问题。随后,有关学者针对荷载速率对混凝土性能的影响开展了大量研究,如刘鹏等[6]运用试验与仿真结合研究了应变速率对混凝土抗压极限强度及变形特性的影响,表明混凝土材料在动载作用下强度、应变、弹性模量、泊松比等力学指标与准静态荷载作用下差异显著;李富荣等[7]通过对混凝土试件展开受压、劈拉和受剪动力性能试验,研究混凝土破坏形态与应变率间的关系;杜荣强等[8]指出混凝土动力本构受混凝土应变率影响显著,研究混凝土疲劳耐久性应考虑应变率。
围绕列车荷载对无砟轨道疲劳损伤的研究,刘丹[9]运用疲劳本构模型,预测了CRTSⅠ型板式无砟轨道在列车荷载、温度荷载、混凝土冻融等因素作用下的疲劳寿命;POVEDA[10]通过数值仿真与试验相结合的方法,研究了轨道板振动模态和时变荷载作用下的瞬态效应,提出了应力幅影响下的一种疲劳准则;傅强等[11]基于统计损伤力学建立了CA砂浆应变率本构模型,研究了CRTSⅡ型板式轨道砂浆层的应变率效应;LI等[12]通过霍普金森杆实验研究了不同应变率下自密实混凝土的动态力学特性;徐浩等[13-14]针对板式轨道混凝土和水泥乳化沥青砂浆层展开应变速率相关研究,明确了列车荷载作用下轨道板应变率的量级。上述关于无砟轨道疲劳损伤及混凝土应变率的研究,多关注于轨道结构整体疲劳特性及应变率对混凝土性能的影响,但对轨道板内应变率分布规律的研究相对较少。
目前,无砟轨道结构设计在参照有砟轨道铺设经验和路面工程设计经验的基础上,建立系统的设计方法[15],但高速列车荷载具有超高周期、超高频率的特性,轨道板应变率对结构疲劳耐久性的影响不容忽视。因此,有必要深入探究无砟轨道在服役过程中的应变率分布规律,为进一步解决无砟轨道结构动力疲劳损伤问题提供理论基础。
1 纵连式轨道动力分析模型
根据纵连板式轨道的结构特点,基于车辆-轨道耦合动力学理论,建立高速列车作用下轨道结构分析模型,如图2所示,并作如下假定。
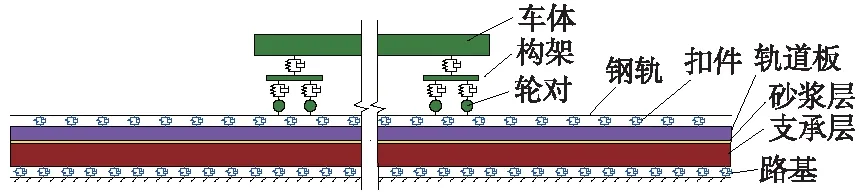
图2 列车-轨道-路基系统动力学模型
(1)轨道结构各部件视为均匀线弹性体。
(2)轨道结构主要承受垂向轮轨力作用,忽略环境因素的影响。
(3)忽略假缝、侧向挡块等附属结构对轨道结构动力特性的影响。
1.1 列车-轨道-路基系统动力学模型
轨道系统视为多层弹性结构体系,采用有限单元法建模求解。为消除边界效应并确保列车运行数据稳定,建立8块轨道板(全长52 m)进行仿真模拟,并以中间第4、5块板为主要研究对象。钢轨为CHN60型U71MnG,采用弹性支承的铁木辛柯梁模拟;扣件系统主要考虑其垂向刚度,将其等效为离散线弹性单元,采用力元单元模拟。纵连式道床结构视为空间层状黏弹性体,主要为轨道板、宽窄接缝、砂浆层和混凝土支承层,采用空间六面体实体单元模拟,并忽略结构的初始伤损,层间采用黏接方式进行连接。轨道模型采用自由网格划分,精度为0.03 m。轨道结构模型主要参数如表1所示。
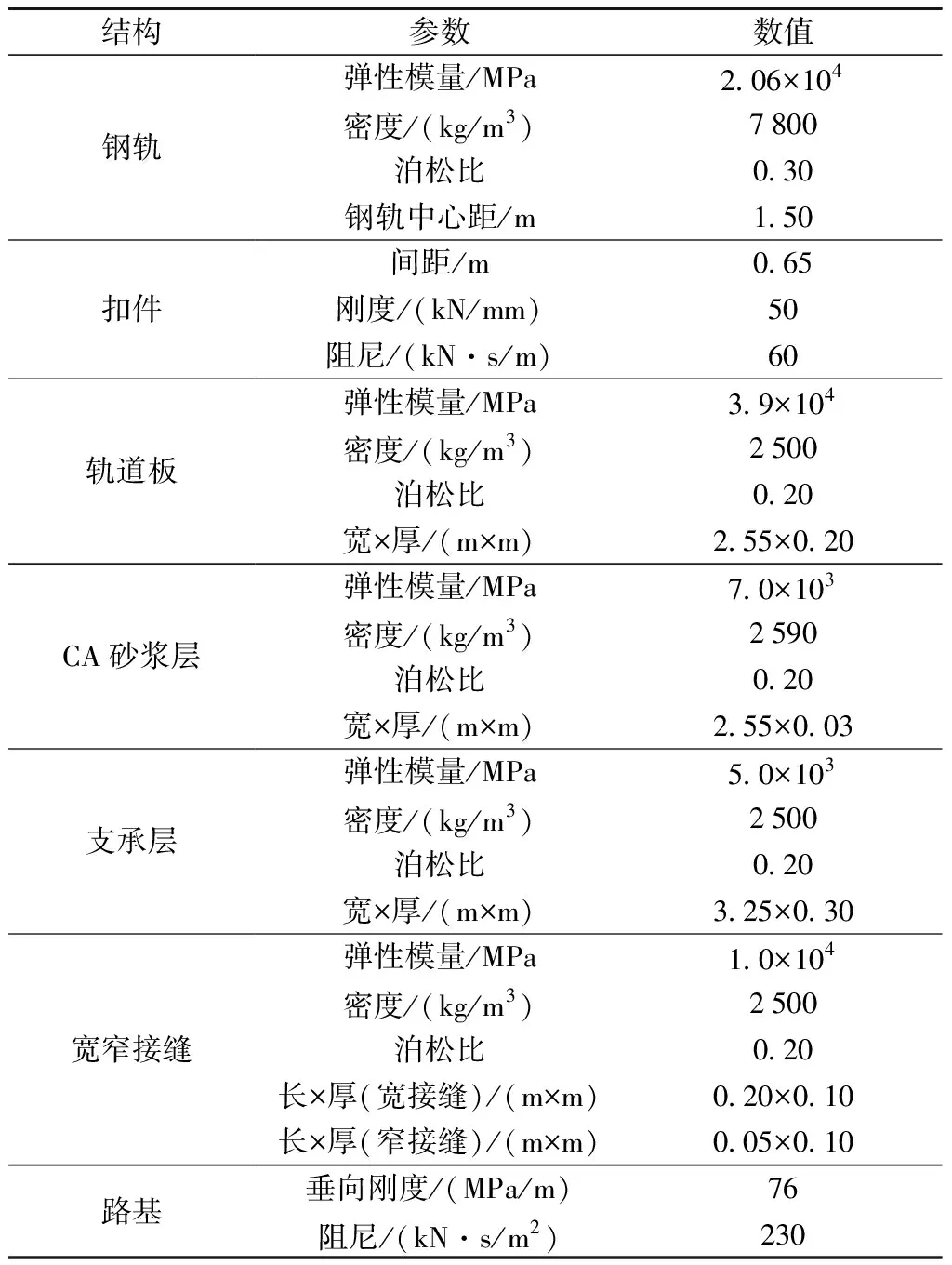
表1 轨道结构模型主要参数[16-17]
以CRH2[18-19]型高速列车为例,考虑单节车辆,建立包括1个车体,2个构架,4个轮对组成的多刚体动力学模型。车辆刚体模型与柔性轨道模型通过轮轨接触位移和轮轨作用力相互协调关系进行连接。考虑车辆悬挂系统中的非线性因素,轮轨之间的相互作用采用多点接触模型模拟,法向作用力由赫兹非线性弹性接触理论[20]确定。轨道不平顺采用德国低干扰谱。
1.2 模型验证
为验证建立的车辆-轨道-路基垂向耦合系统动力学模型的正确性,仿真计算了行车速度300 km/h下转向架左前轮轮轨垂向力、模型中部钢轨垂向位移、轨道板垂向位移和钢轨支点反力等动力响应,图3为列车转向架左前轮轮轨垂向力时程曲线,各项仿真指标最大值与文献[16]对比结果如表2所示。
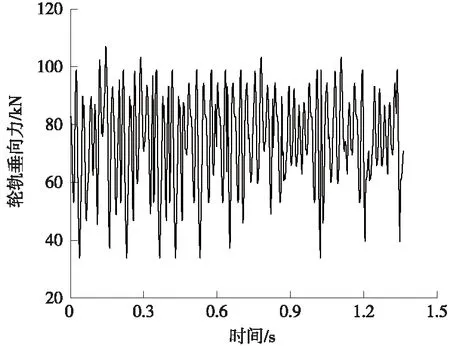
图3 轮轨垂向力仿真结果时程曲线

表2 仿真结果与文献[16]对比
分析表明,轨道结构关键参数的模型计算结果与实测或文献仿真结果相对误差均在20%范围内,可以认为,上述建模方法得到的纵连式轨道动力仿真模型可用于探讨道床结构的动力响应等问题。
2 纵连板式无砟轨道应变率分布规律
2.1 分析点位分布
为深入分析高速列车荷载作用下轨道结构应变率的分布规律,主要选取:Ⅰ断面—宽窄接缝横截面,Ⅱ断面—轨道板中横截面,Ⅲ断面—轨道板中纵断面,Ⅳ断面—钢轨下方纵断面等4种典型截面进行分析,各断面布置如图4所示。

图4 代表性研究截面示意
其中,点a为截面Ⅰ与截面Ⅳ交点处,即钢轨位置下宽窄接缝处;点b为截面Ⅱ与截面Ⅳ交点处,即为轨道板中扣件处。
断面上具体分析点位布置如图5所示。研究沿垂向应变率分布时,在a、b处设置沿垂向的6个分析点,如图5(a)所示,因分析对象主要为轨道板和CA砂浆层,故混凝土支承层不做分层处理。进行沿横向应变率分布规律研究时,在截面Ⅰ、Ⅱ各设置9个横向分析点,布置如图5(b)所示。分析应变率沿纵向分布特点时,在截面Ⅲ、Ⅳ上宽窄接缝处、扣件处和扣件间均设置分析点,各21个,布置如图5(c)所示。
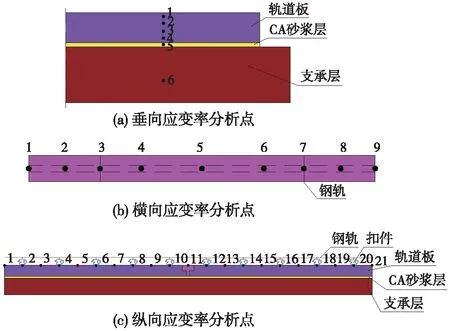
图5 断面分析点位布置
2.2 无砟道床应变率分布规律
应变率作为空间某点上的应变随时间的变化,通过求解结构内应变时程,再对时间进行一阶求导,计算得到轨道结构各部分的应变速率。以图4中b点处轨道板结构为例,计算得到轨道板该处的应变率时程曲线,如图6所示。
图6表明,在列车通过时,轨道板结构b点处最大应变率为6.0×10-4/s,其最大应变率大致发生在车辆运行至b点上方时,故取应变率时程曲线最大值进行分布规律分析。

图6 轨道板应变率时程曲线
根据各向分析点位布置情况,分析无砟道床应变率的分布特性,如图7所示。
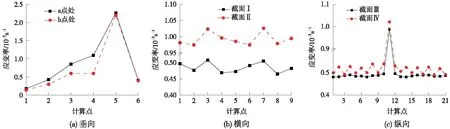
图7 无砟道床典型断面处应变率峰值分布曲线
图7结果表明,当列车运行速度为300 km/h时,纵连式轨道各部分结构最大应变率处于4.0×10-4/s~2.3×10-3/s范围。图7(a)表明,板上表面主要承受压应力,其应变率峰值约为3.0×10-4/s;下表面主要承受拉应力,其应变率峰值约为1.2×10-3/s,是上表面受压区的4倍。受砂浆层弹性影响,该层应变率最大,达2.3×10-3/s。通过上述分析发现,无砟道床等层状结构受拉区应变率变化更为突出,故在进行轨道板后续纵、横向分布规律探究时,采用应变率较大的受拉区,即图5(a)中点4处应变率探究轨道板纵、横向应变率分布规律。图7(b)表明,轨道板中分析点3、点7处应变率略大于其余分析点处,这是由于该分析点处于扣件系统正下方,直接承受列车荷载作用;其余分析点沿轨道横向的应变率峰值分布较为均匀。图7(c)表明,截面Ⅲ(轨道板中纵截面)纵向应变率分布较为均匀,截面Ⅳ(钢轨下方纵截面)中扣件正下方处轨道板峰值应变率均大于两扣件中点处,这是由于扣件直接承受列车荷载,并传递至轨道板上;且截面Ⅳ纵向应变率整体略大于截面Ⅲ,纵连式轨道结构轨道板峰值应变率约为5.2×10-4/s,宽窄接缝处约为1.1×10-3/s,受结构构造及材料差异等影响,宽窄接缝处应变率显著增长近2倍。
综上,无砟道床应变率在垂向最为敏感,垂向各层中砂浆层更易发生伤损;横向上,各水平差异不大;纵向上,结构层间和集中受力处存在应变率突变现象,宽窄接缝问题较为突出,层内差异较小。故应密切关注砂浆层及宽窄接缝处的应变率变化规律。
2.3 宽窄接缝对应变率影响
宽窄接缝受结构特征、施工工艺、环境条件、浇筑质量与时机等限制,是纵连板式轨道的薄弱环节。下面讨论窄接缝沿垂向厚度及纵向宽度等尺寸变化,对轨道垂向应变率的影响。其中,窄接缝沿垂向厚度尺寸分别取50,100,150,200 mm,沿纵向宽度分别取25,50,75,100 mm,计算结果如图8所示。
图8结果表明,纵连板式无砟轨道各部分结构垂向应变率均随着窄接缝厚度增大而减小,相较于窄接缝原始厚度100 mm,厚度增加1倍时,应变率减小5.0×10-4/s。结构垂向应变是垂向位移变化量与板厚的比值,纵连板式无砟轨道在列车荷载作用下主要承受垂向力,故板厚是影响垂向应变率的控制因素。改变窄接缝宽度时,各部件应变率变化均小于1.0×10-5/s,故宽度对结构垂向应变的影响可忽略不计。
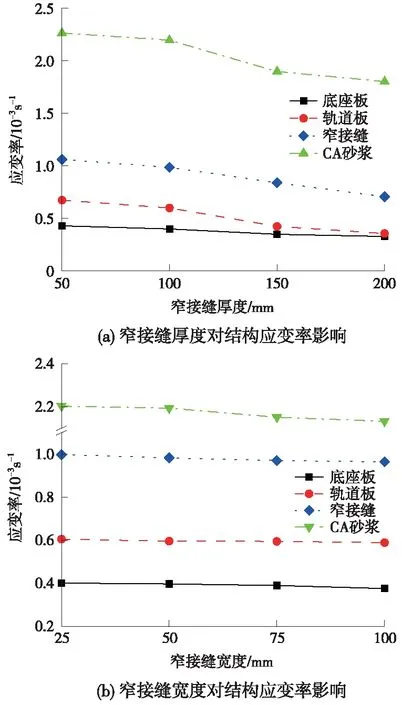
图8 窄接缝尺寸对轨道结构应变率影响曲线
2.4 砂浆层对应变率影响
CRTSⅡ型板与底座之间设有高弹模的水泥沥青砂浆调整层,其弹性模量对轨道板及自身的受力与变形影响甚大。在砂浆层常见刚度范围内选取弹性模量6 000~10 000 MPa进行讨论,各部件应变率峰值如图9所示。

图9 砂浆层弹性模量对轨道结构应变率影响
图9结果表明,砂浆层弹性模量变化对轨道部件应变率影响较小;砂浆层应变率随着自身刚度的增加而略有降低。因此,在分析轨道结构应变率时可忽略砂浆层弹性模量的影响。
3 结论
采用有限元软件和多体动力学仿真软件建立了车辆-轨道-路基垂向耦合动力学模型,研究了纵连板式无砟轨道的动态应变分布规律,得到如下结论。
(1)板下缘受拉应变率峰值为板上缘受压应变率峰值的4倍,是轨道板应变率的重点关注区域。随着有限元软件和多体动力学软件的发展应用,在建立车辆-轨道-路基垂向耦合动力学模型时,为更加准确地模拟轨道结构应变率,建议细化板状结构沿垂向应变率计算。即各结构层平均应变率峰值与板下缘受拉应变率峰值存在较大差异。
(2)纵连板式轨道的垂向应变率变化较纵、横向更为敏感,纵、横向结构仅在结构层间和受集中力处有明显增幅,层内差异较小。
(3)纵连板式无砟轨道结构中,砂浆层和窄接缝处应变速率较其他轨道结构更大,在进行动力研究时建议着重关注。
(4)轨道结构应变率对结构厚度变化较为敏感,宽度和弹性模量等参数对部件应变率影响较小。
