基于PSO优化的激光末制导炮弹诸元解算方法
2022-06-06王治霖王武刚周永佳
徐 超,王治霖,王武刚,周永佳,白 婵
(1 北京理工大学宇航学院,北京 100081;2 西北工业集团有限公司,西安 710043)
0 引言
为保证末制导炮弹命中率,需要提供较高精度的射击诸元,即对射表精度有较高要求。诸元解算指炮弹发射前,根据实际发射条件和武器系统状态计算出一组准确的诸元值,装订在武器系统上使其满足要求,精确完成打击任务。射击诸元主要包括:装药号、射角(以下称表尺)、发射方位角(以下称方位)、机械陀螺工作时间(以下称程装)、激光照射起始时间(以下称延迟)等。诸元解算时,需考虑导引头视场范围、过载能力、末制导段速度、射程等多约束条件;需考虑气象条件(包括温度、地面气压、横风、纵风等)、马格努斯效应、药温等因素;需考虑延时、程装、表尺、方位等多输出问题。因此,可将诸元解算看成是一种具有多输入多输出的参数优化问题,需要空间和时间双维度耦合迭代的复杂寻优计算。
目前,诸元解算存在以下问题:
1)弹道解算过程主要通过弹道积分的方法获得导弹落点,涉及六自由度非线性微分方程的数值求解,导致弹道计算耗时较长,对作战任务中的时敏目标精确打击极为不利。
2)需根据当地气象条件,查询预先装订的射表,修正上述各影响因素。但这种方法解算精度较差,降低作战效能。
针对上述问题,Ollerenshaw等基于弹丸线性理论,简化了六自由度方程,推导了控制力作用下的弹丸转向幅值和角度计算公式,结果与六自由度方程结果接近,但没有考虑风的影响且是平射弹道。Hainz等提出了基于弹丸修正线性理论的快速弹道预测方法,相较于非线性六自由度、三自由度和质点弹道数值积分进行弹道预测方法,具有计算机占用资源少及计算精度高等优点,但为保证全弹道预测精度,弹丸线性理论在计算弹道时需实时更新迭代多次,使得解算复杂、数据量大,降低了弹道解算的实时性。丁天宝等创建了适应宽海拔的弹道解算新方法。考虑非线性姿态运动,建立了阻力系数随海拔高度变化的模型,研究结果表明新型弹道解算方法具有较高精度,适用于宽海拔作战。赵东华等研究应用二分法求根的思想求解外弹道方程组,从而决定了火炮射击诸元的算法,但若想得到较高精度的诸元,需要积分的次数会随之增加,计算量依旧较大。陈瑞军等针对研究初期确立的基本诸元计算方法不能满足有效攻击区战技指标及计算速度慢等问题,提出了将有效攻击区中心为表载射程及简化的弹道模型用于诸元计算的方法,但有效攻击区中心需要计算诸多弹道,再计算捕获区域的中心,若区域为不规则,精度可能会较差。
针对激光末制导炮弹诸元精确解算的需求,文中提出了一种基于PSO(particle swarm optimization)算法优化的基本诸元解算方法。首先,分析作用力和气动力,建立末制导炮弹的六自由度动力学和运动学方程组,构建仿真模型。介绍了大气模型,并分析高度、虚温、气压、风速、风向数据对空气密度、声速、马赫数等影响;其次,应用龙格-库塔法对六自由度动力学和运动学方程组进行解算。给出气动参数辨识方法,进行弹道校验;再次,分析了表尺、程装等参数变化时,对射程和射高的影响,将其作为变量,应用粒子群算法优化得到最优解,作为射表相应的诸元解算结果。最后,将模型经PSO优化后进行仿真和实际打靶验证,结果表明,无论是仿真验证还是实际打靶试验,这种方法精度更高,耗时更短,可满足实战化需求。
1 弹丸的弹道模型
末制导炮弹由舵机、导引头、发动机、惯性陀螺、尾翼等分部件组成,包含气动、动力、控制、制导等系统。由于各系统部件参数、气象测量、发射平台均存在误差,若要在各种误差下仍能精确命中目标,需建立更加精确的弹丸模型。
1.1 气动力及作用力分析
末制导炮弹在飞行过程中,不同阶段其气动布局均有变化,主要气动布局如表1所示。

表1 气动布局
根据不同飞行模式代入对应参数,使模型更加准确。为得到准确的飞行数学模型,根据表1中不同的气动布局进行理论值计算及风洞试验,得出各状态下的阻力系数、升力系数、传递比、滚转力矩系数等气动参数。对于末制导炮弹,一般情况下有两种运动状态:一种是用于近距离射击,称为近区弹道;另一种是用于远距离射击,称为远区弹道。以远区为例,末制导炮弹的弹道组成如图1所示,分为以下5段:
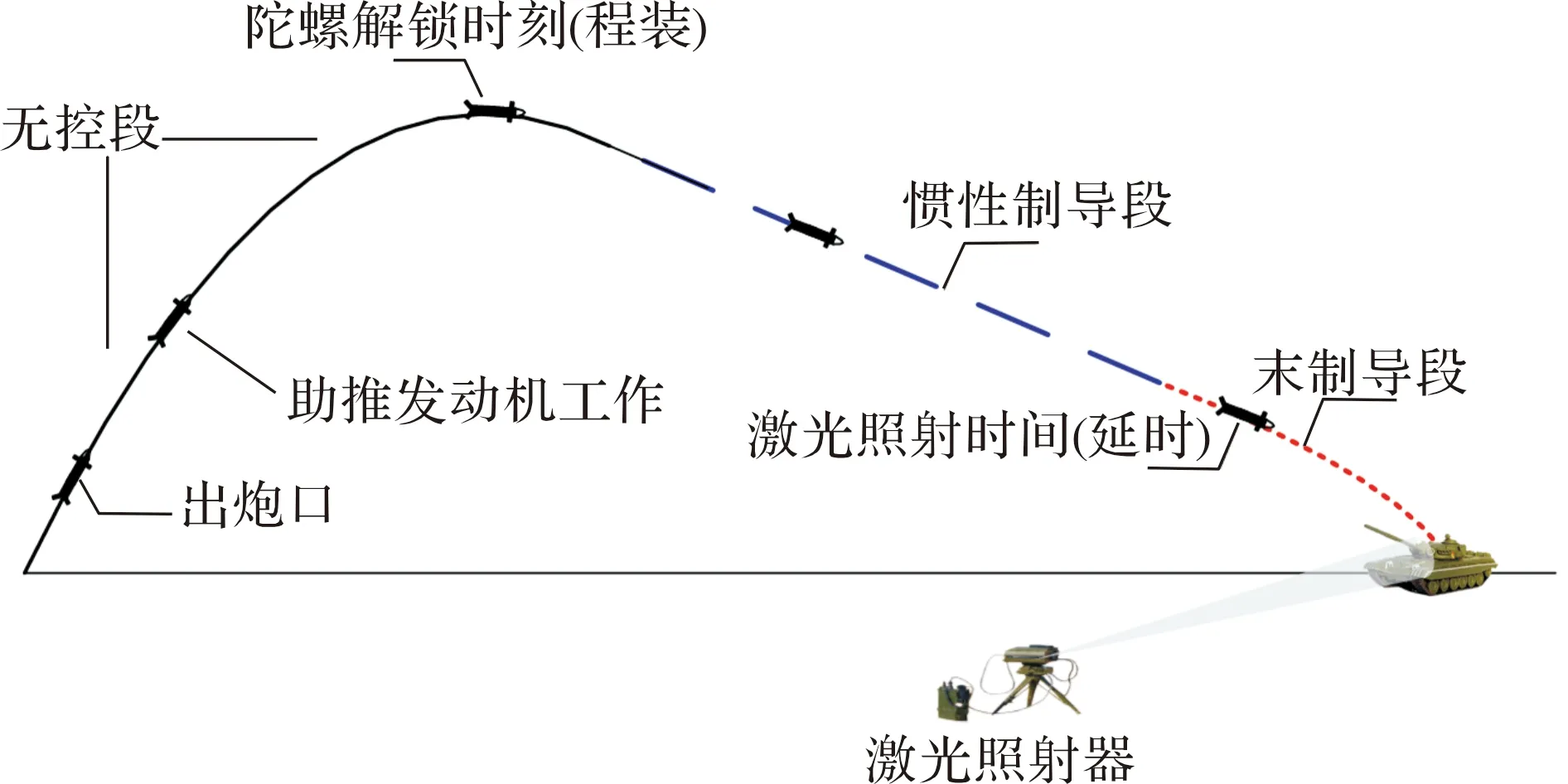
图1 弹目之间角度关系
1)出炮口无控段:出炮口后末制导炮弹以低速旋转的无控方式飞行,直至发动机工作;2)助推发动机工作段:发动机开始工作使炮弹的速度增加,从而延长飞行距离;3)助推发动机结束工作后无控段:助推发动机工作结束后,炮弹仍以低速旋转的无控方式飞行;4)惯性制导段:陀螺解锁后,惯性系统开始工作,为增加射程及末制导距离,此阶段通过重力补偿的方式使炮弹基本按直线飞行;5)末制导段:激光开始照射发出信号,当炮弹导引头接收到目标反射的信号时,炮弹开始转入末制导段,直至命中目标。
对于近区弹道,由于助推发动机不工作,同时也不需要滑翔增大射程,因此近区弹道仅由自由飞行段和末制导段组成。
末制导炮弹在飞行过程中所受的外力主要是空气动力,可分解为阻力、升力和侧向力,其表达式为:
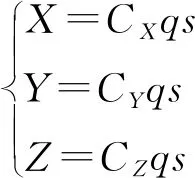
(1)
式中:,,分别代表阻力、升力、侧向力;、、为升力系数、阻力系数、侧向力系数;为动压头;为参考面积。由计算和风洞试验得出,发动机推力可表示为:
=+(-)
(2)
式中:为每秒燃料的消耗量;为燃气在喷口喷出的速度;为发动机喷口截面积;为喷口截面处燃气流压强;为喷口周围的大气静压强。此外对于舵机控制力,以有两对舵为例,即上下舵(2舵、4舵)和左右舵(1舵、3舵)。对于左右舵:
=
(3)
式中:为舵片效率;为左右舵的舵偏转角,沿上偏为正。对于上下舵:
=
(4)
式中:为上下舵的舵偏转角,沿右偏为正。
1.2 弹道方程建立
弹丸的刚体六自由度弹道方程能够准确表示弹丸的飞行运动状态,建立运动学模型和动力学模型。质心运动动力学方程为:

(5)
式中:为炮弹实时质量;为炮弹飞行速度;为发动机推力,由气动数据进行插值得到;、分别为攻角、侧滑角;为弹道倾角;为速度倾斜角;为弹道偏角。绕质心转动动力学方程为:

(6)
式中:、、分别为飞行器在弹体坐标各轴的转动惯量;、、分别为飞行器受外力对质心产生的力矩在单体各轴上的投影;、、分别为飞行器绕质心旋转的俯仰、偏航、滚转角速度。质心运动方程为:
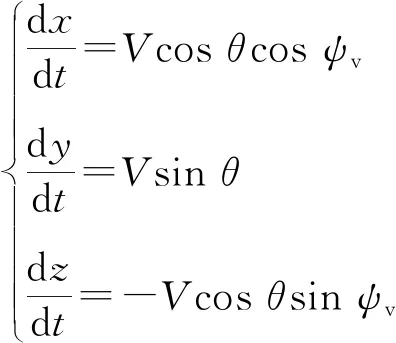
(7)
式中:、、分别为飞行器质心的位置坐标。绕质心转动运动学方程为:

(8)
式中:ϑ、分别为飞行器的俯仰角、偏航角。发动机工作时,炮弹质量变化方程为:
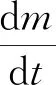
(9)
式中:为质量秒流量。角度关系为:
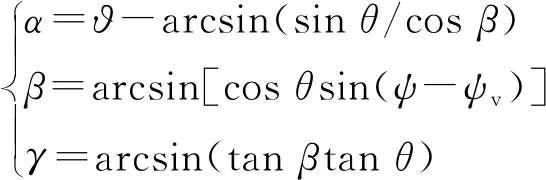
(10)
对于惯导段,其弹道为重力补偿弹道,即重力沿垂直于速度方向的法向分量与攻角产生的补偿升力之间存在平衡关系。这种平衡关系可保证飞行时其纵轴对地平面的倾斜角基本不变,增大射程。
在末制导段上,延时开始时刻,导引头开始工作,测量出弹目线旋转角速度,再根据过重力补偿的比例导引制导律给出对舵机的控制信号,修正纵向和横向偏差,直至命中目标。末制导原理框图如图2所示。

图2 末制导原理框图
1.3 气象模型
对于气象数据,由气象雷达车测量地面和高空的气象条件进行采集,包括气温、气压、风速、风向等。以2021年9月7日在某靶场一次飞行实验为例,以200 m分层的气象数据如表2所示。
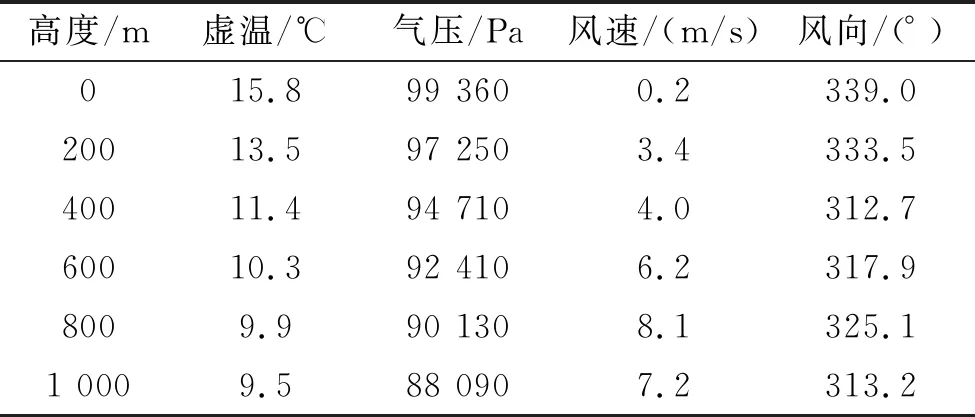
表2 气象数据
对表2进行插值,即可得到不同高度下的虚温、气压、风速、风向数据。对于虚温,需将其数据转换为开氏温度。对于不同表尺和程装数据,弹道高度都不相同。因此在应用此表格时,高度应覆盖弹道高。下面分析这些数据变化对空气密度、声速等的影响。首先分析对空气密度的影响:
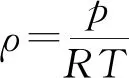
(11)
式中:为气体常数,其值为287.14;为当前高度下的气压;为当前高度下的温度;为当前高度下的空气密度。其次,分析对声速的影响:
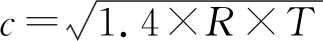
(12)
式中:为当前高度下的声速。最后,对于当前高度下的风速和风向,主要影响弹丸的速度。声速和来流速度对当前高度的马赫数影响,可表示为:

(13)
2 模型方程解算及弹道模型校验
2.1 模型方程解算
对于上述六自由度微分方程,常用的微分方程的数值解法有欧拉法、龙格-库塔法等。欧拉法的特点是简单易行,但精度低。在同样计算步长的条件下,龙格-库塔法的计算精度要比欧拉法高,因此采用龙格-库塔法计算六自由度微分方程。设有一阶微分方程:

(14)
若已知时刻的参数值,则可用龙格-库塔法求+1=+Δ时刻的+1的近似值,龙格-库塔公式为:

(15)
四阶龙格-库塔法每积分一个步长,需要计算4次右端函数值,并将其线性组合求出被积函数的增量Δ。四阶龙格-库塔法除了精度较高外,还易于编制计算程序,改变步长方便,是一种自启动的单步数值积分方法。因此,对于六自由度微分方程采用此方法进行解算。
2.2 弹道模型校验
飞行试验可获取丰富的测量信息,包括地面雷达获取的速度、位置信息以及弹上黑匣子惯性测量数据,利用这些数据可识弹道模型重要的气动参数,实现弹道模型的高置信度校验。
气动参数是弹道模型构建的基础参数,常用的参数辨识方法有最小二乘法、最大似然、最小方差、最小风险等。文中应用牛顿-拉夫逊算法求解气动参数辨识问题,气动参数辨识的具体过程如下:
步骤1:输入初始数据。参数的初估值,状态初值;待估计参数的上限和下限值;动力学系统试验的观测量和控制量输入的实测值,即经预处理后的雷达数据。
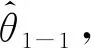
步骤3:准则函数的计算。利用模型输出值和实测数据,求得准则函数。
步骤4:噪声协方差矩阵计算。利用模型输出值和实测数据求得该矩阵。
步骤5:待识别参数增量Δ的计算。通过牛顿-拉夫逊算法的迭代公式求得本次迭代增量。并通过灵敏度公式计算出灵敏度。
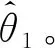
在上述过程中,待辨识参数的迭代初值通常取过去的试验值或理论计算值。的上限和下限按待辨识参数的物理意义,结合实际情况给定,收敛指标则根据精度要求进行取值。
3 基于粒子群的诸元解算
3.1 参数分析
分析表尺、程装等参数变化对射程将产生影响。采用控制变量法,分别对远区及近区两种运动状态进行分析。
对于近区弹道,由于助推发动机不工作,同时也不需要滑翔增大射程,因此只考虑表尺变化时对射程的影响。选取初速为326 m/s的炮弹,无程装,对表尺为300 mil、350 mil、400 mil进行仿真,仿真结果如图3所示。

图3 表尺变化对初速为326 m/s无程装炮弹射程的影响
由图3可知,对于近区弹道,当表尺增大时,射程及射高都同时增大。对于远区弹道,分析表尺变化时对射程的影响。选取初速为760 m/s的炮弹,固定程装为110分化,对表尺为480 mil、500 mil、520 mil进行仿真,仿真结果如图4所示。

图4 表尺变化对初速760 m/s固定程装110分化炮弹射程的影响
由图4可知,与近区弹道相同,当表尺增大时,远区射程及射高都同时增大。分析程装变化对射程的影响,选取初速为760 m/s的炮弹,固定表尺为500 mil,对表尺为105分化、110分化、115分化进行仿真,仿真结果如图5所示。
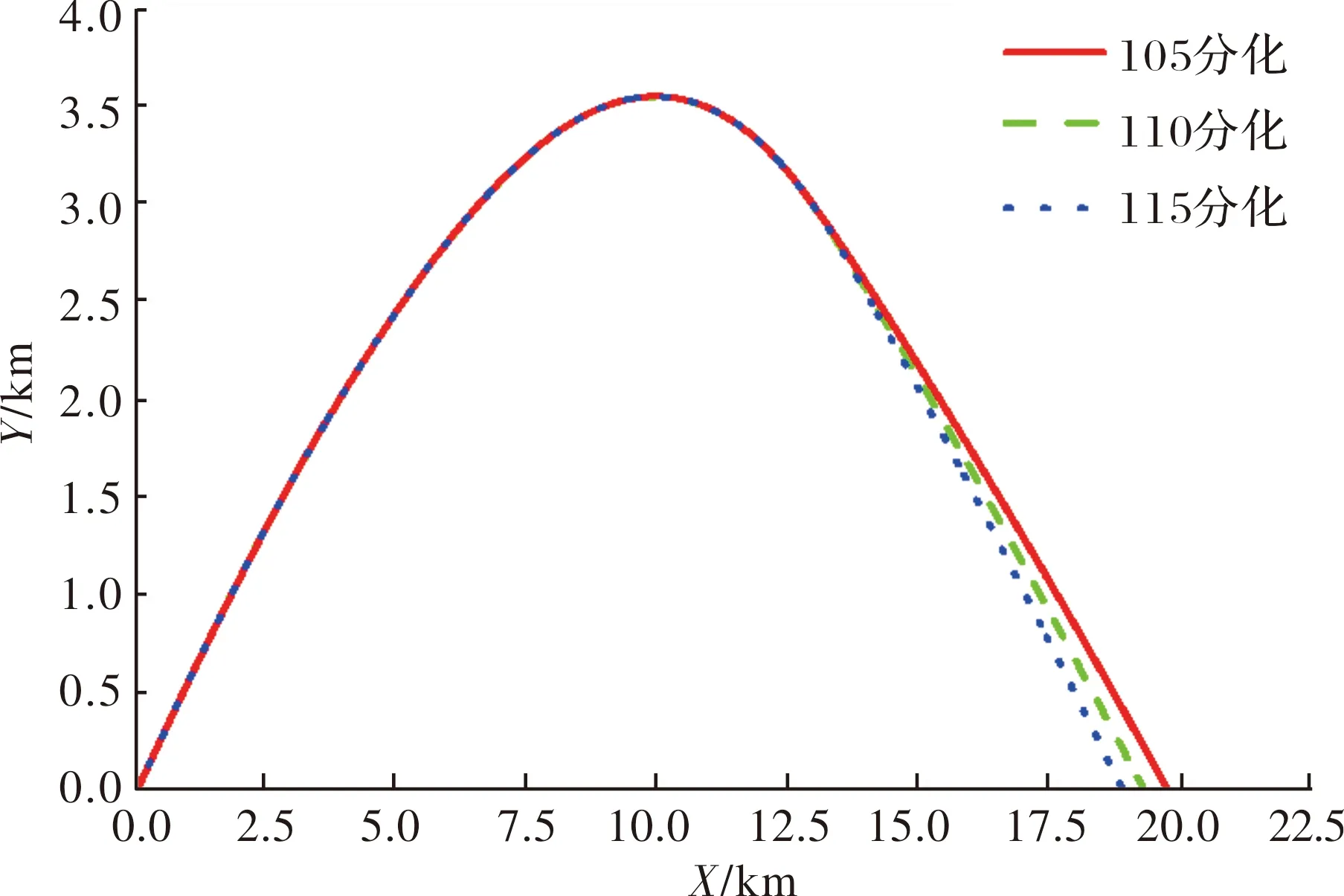
图5 程装变化对初速760 m/s固定表尺500 mil炮弹射程的影响
由图5可知,当程装时间增大时,射程增大,但对射高并无明显影响。由上述分析可知,无论近区还是远区弹道,不同参数对射程均有不同影响。同时,对射高有一定影响,再次证明了气象数据中高度需覆盖射高,否则会对弹道产生较大影响。
3.2 基于粒子群的诸元解算方法
诸元解算要考虑的因素较多,包括气象条件、药温、马格努斯效应等;同时,所考虑的约束条件较多,包括期望射程、程装与惯性陀螺工作的角度范围、导引头有限视场角、弹体机动过载能力、末制导段速度等均应满足弹丸的使用要求;诸元解算的输出量较多,包括表尺、方位、程装、延时等。
对于多输入多输出的参数优化问题,粒子群算法具有参数少、执行效率较高等优点,可以在有限计算量下得到全局最优解。粒子群算法所有的粒子都有一个由被优化的函数决定的适应度值,每个粒子速度决定他们的飞行的方向和距离,粒子群们就追随当前的最优粒子在解空间中搜索。
粒子群初始化为一群随机粒子,然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个“极值”来更新。第一个就是粒子本身所找到的最优解,这个解叫做个体极值;另一个极值是整个种群目前找到的最优解,这个极值是全局极值。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
粒子位置可以用一个维的向量来表示,第个粒子位置表示为:=(,1,…,,,…,,),第个粒子的局部极值位置为=(,1,…,,,…,,),全局最优解的位置=(,1,…,,,…,,)第个粒子的速度为=(,1,…,,,…,,)。在找到粒子的位置和速度,以及局部极值和全局最优解的位置之后,粒子根据下面两个公式来更新自己的位置和速度:
=·,+·rand(,)·(,-,)+
·rand(,)·(,-,)
(16)
=,+,
(17)
式中:,是粒子的第维速度;是粒子速度的惯性系数;、是两个非负常数,称为学习因子,分别调节向个体最优解和全局最优解方向飞行的步长;rand(,)是随机函数,产生在区间[0,1]的随机数;,是粒子的第维位置;,是粒子的局部极值在第维的位置;,是粒子的全局最优解在第维的位置。
由于表尺、程装等参数变化对射程有较大影响,因此将具有决定性作用的表尺、程装等作为变量,为其初始配置位置与速度,生成一群随机粒子。根据各项约束条件及期望射程,设计相应的复合适应度函数。设定学习因子,通过速度和位置的更新得到新的粒子群,利用经校验的弹道模型,计算各粒子的适应度值并选择当前的个体极值,结合全局极值,为下一次的粒子更新提供依据。经过多次迭代,最优粒子即为最终的最优解,作为诸元取值。适应度函数可表示为:

(18)

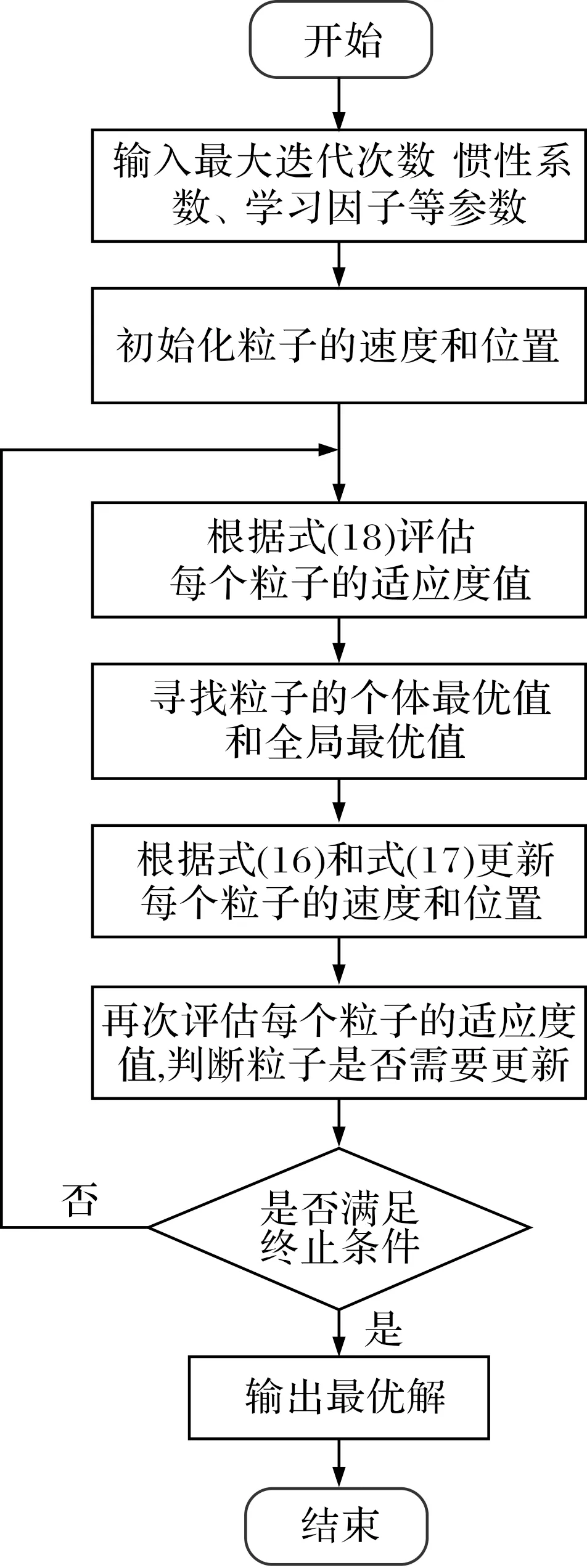
图6 解算流程
4 仿真与飞行试验验证
为验证经PSO优化后模型的准确性和可行性,试验分两部分进行。可行性是指验证弹道解算模型能否应用在实际中,是验证中最为重要的一环。以2021年9月7日在某靶场一次飞行实验为例,进行验证。
4.1 仿真验证
此次飞行试验的期望飞行距离为5 020 m、5 508 m、5 975 m,为近区弹道,根据各装药号的射程覆盖,3次试验均选择初始速度为326 m/s的炮弹。采用气象雷达车测量了地面和高空的气象条件,包括气温、气压、风速、风向等。根据雷达测量,炮位基准位置为1 640 m。以期望射程5 000 m为例,将气象及期望射程等参数输入到模型中,通过粒子群算法优化后,输出的表尺及飞行总时间(可求出程装、延时)值如图7所示。

图7 表尺及飞行时间的预测值
如图7可知,表尺为322.933 mil,飞行时间为20.049 9 s。通常情况下射角为整数值,飞行时间取两位小数,因此射角为323 mil,飞行时间为20.05 s。同样的方法计算得出5 500 m时,射角为379 mil,飞行时间为23.12 s;在6 000 m时,发射角为449 mil,飞行时间为26.75 s。无控飞行弹道如图8所示。
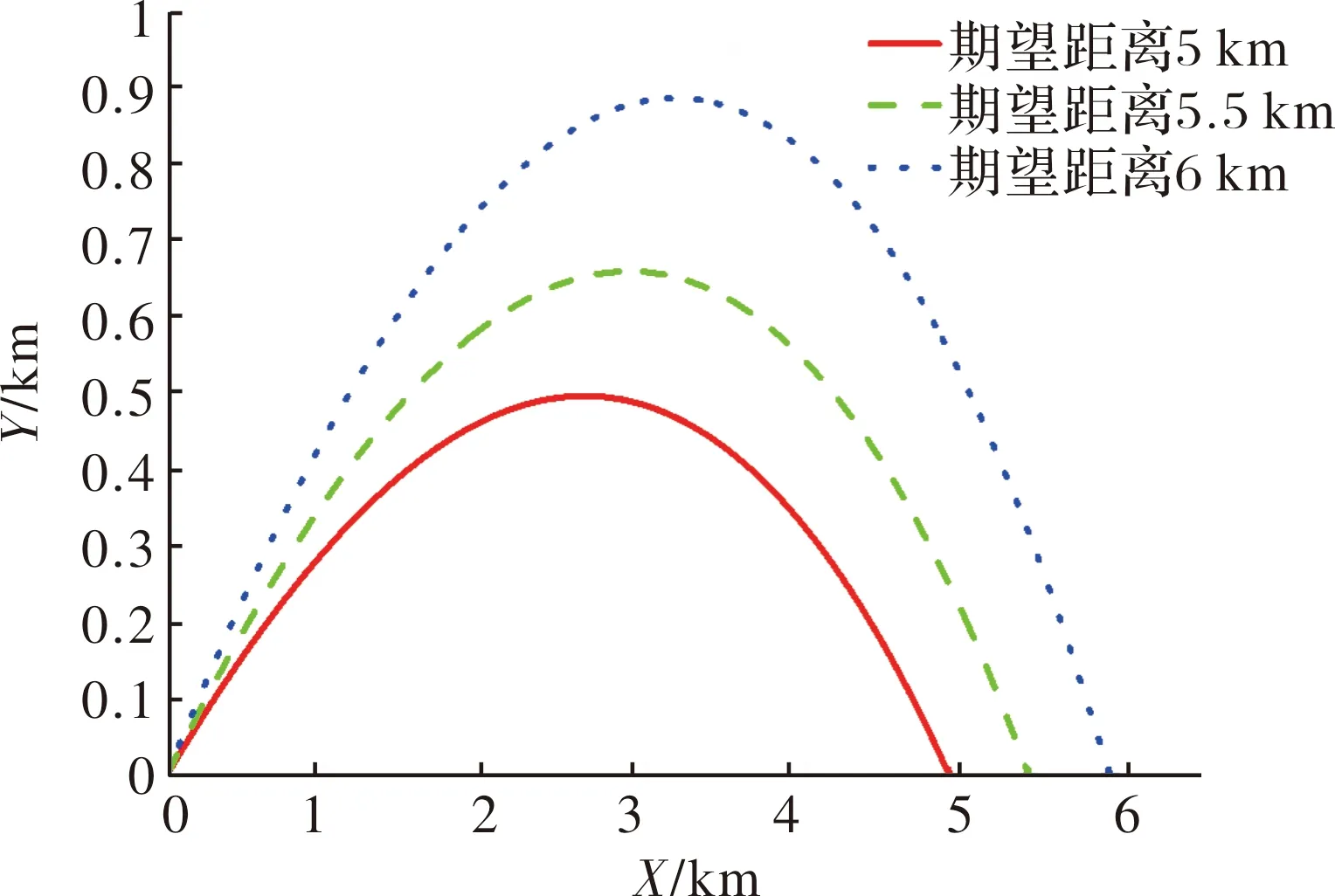
图8 飞行弹道
从图8可以看出,实际射程与期望射程的误差满足诸元解算的要求。
4.2 实际打靶验证
在某靶场开展激光末制导炮弹飞行试验,对诸元优化方法进行进一步验证。在3个射程下,通过文中的优化方法,得到相应的诸元参数,如表3所示。
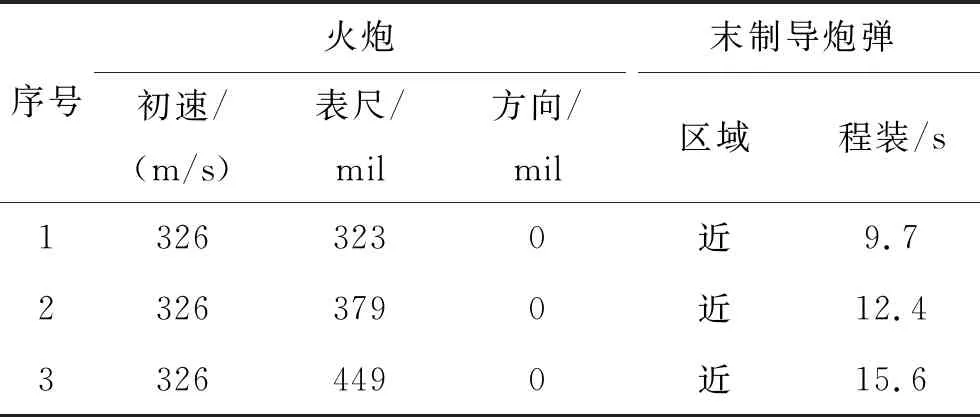
表3 射击诸元
根据上述诸元进行射击,均命中目标,图9为实际中靶效果图。

图9 实际中靶效果图
从图9可看出,基于粒子群优化的射击诸元均可命中目标,脱靶量较小。通过实际飞行实验,进一步验证了这种方法的有效性。
5 结论
通过龙格-库塔法对弹道进行解算,给出气动参数辨识方法分析了表尺、程装等参数变化对射程将产生影响;应用粒子群算法优化得到最优解,作为射表相应的诸元取值。通过仿真和实际打靶验证说明了弹丸模型经粒子群算法优化后准确性高、可行性强。
该模型对实际工程应用提供了参考。
