炸药爆轰对金属壳体加速能力研究进展
2022-06-06王伟力梁争峰阮喜军
李 鑫,王伟力,梁争峰,阮喜军
(1 海军工程大学兵器工程学院,武汉 430033;2 西安近代化学研究所,西安 710065)
0 引言
凝聚相炸药在军用和民用领域已经使用了一个多世纪,其中一个主要特征是其固有的亚稳态,即在给定的刺激下容易爆炸。例如,当引爆扩爆装置在炸药中形成爆轰波时,炸药瞬间爆轰转化为高温高压膨胀的混合气体,并作用于周围介质。最为典型的是,炸药被一个金属外壳包围,当炸药爆轰后,爆轰气体产物将巨大的压力和应变率(通常为10~10s)施加于壳体内壁,从而迫使外壳形成裂纹并延径向扩展,裂纹首先出现在壳体外表面,然后向内部生长,等到裂纹贯穿壳体后,最终金属外壳破裂形成碎片,并被高速驱动,同时爆轰气体产物压缩空气形成冲击波。
从炸药爆轰、壳体破裂、碎片抛射再到空气中压缩形成冲击波超压整个过程来看,这是炸药爆炸作功能力的总和,对于杀伤弹药而言,碎片抛射速度是弹药毁伤的重要参数,即金属加速能力,它是指炸药爆炸形成的爆轰波及爆炸产物对接触的金属壳体破碎后形成的碎片加速作用的能力,金属加速能力越强,弹药毁伤威力越大。因此,研究炸药爆轰对金属加速能力具有重要的意义。
文中概述了炸药爆轰金属壳体加速的过程,介绍了金属加速能力的评价指标,总结并分析了国内外针对炸药格尼速度提出的3类计算方法,分析了炸药格尼速度的影响因素。
1 金属加速过程及评价指标
1.1 金属加速3个阶段
炸药起爆后,爆轰波在炸药中传播,到达金属壳体后形成冲击波的反射,大约1~2 μs后炸药爆轰完全形成高温高压爆轰气体产物,产物膨胀驱动壳体,壳体在高压高应变率条件下迅速膨胀,超过其动态屈服强度后形成裂纹,随即破裂形成碎片。而后爆轰气体产物开始流过裂缝向外溢出,由于爆轰气体产物速度此时仍高于碎片速度,壳体碎片将进一步被加速,直至与爆轰气体产物速度相同,此时达到最大速度,图1所示给出了炸药爆轰金属加速的过程。

图1 炸药爆轰金属加速过程
由图1可知金属壳体加速过程分为3个阶段:
1)第一阶段:炸药爆轰波瞬时加载阶段。由于炸药爆轰反应时间极短,几乎瞬间形成爆轰气体产物,因此一般该过程为定容爆轰。该阶段是由爆轰波阵面的高压区引起的,爆轰波传播至壳体内表面后,驱动壳体给予瞬时速度,该过程时间极短。根据壳体结构的不同,爆轰波可分为滑移爆轰波和正向爆轰波两类。其中,对于圆柱体结构,侧向壳体受到滑移爆轰波的加载,端面盖板则受到正向爆轰波的加载。
2)第二阶段:爆轰气体产物膨胀加载阶段。高温高压爆轰产物膨胀驱动外壳,这个过程几乎不存在与外界的热量交换,属于绝热膨胀。爆轰气体产物膨胀存在一定过程,持续时间比爆轰波加载要长,可达到几十微秒。含铝炸药中铝粉的二次反应一般发生在该阶段,解释了含铝炸药爆速降低但膨胀作功能力增强的原因。同时,该阶段与壳体材质密切相关,当壳体是具有塑性的金属材质时,可在爆轰产物驱动下发生膨胀,且塑性越好,强度越高,壳体膨胀体积越大,爆轰气体产物膨胀加载的历程越长,壳体获得的速度越高。而对于脆性壳体材质,比如陶瓷,炸药爆轰波加载瞬间壳体就碎裂,爆轰气体产物溢出,即不存在壳体膨胀阶段,也就不存在爆轰气体产物膨胀加载阶段。如图2所示给出了爆轰波和爆轰气体产物加载下金属壳体速度-时间曲线,爆轰波加载时间短,对金属加速贡献率大,是第一驱动力,爆轰气体产物加载时间长,是第二驱动力。

图2 爆轰波和爆轰气体产物加载下壳体速度-时间曲线[2]
3)第三阶段:壳体破裂后爆轰气体产物的二次持续加载阶段。王新颖等揭示了金属壳体破裂后爆轰产物继续加速过程的趋势和规律,只是这个阶段在整个金属加速过程中贡献较小,所以往往忽略不计。
从以上3个阶段可知,爆轰波驱动金属壳体速度是一个过程量,由爆轰气体产物驱动壳体达到的最终速度才是需要关注的,对于弹药工程设计及安全防护具有实用意义。
1.2 金属加速能力理论计算

侯俊亮等和张守中等从理论角度推导了炸药爆轰加载下金属壳体应力场、膨胀速度、膨胀角度、破裂半径及碎片速度等参数,在推导过程中作了如下假设:一是炸药瞬时完成爆轰;二是金属壳体简化为理想刚-塑性材料模型,忽略弹性变形;三是金属壳体膨胀过程中仅发生径向运动,忽略轴向运动;四是不考虑初始应力波在金属壳体内的传爆与反射等细微过程。计算表明在金属管膨胀的开始阶段膨胀角和径向膨胀速度是逐渐增大的,等达到稳定爆轰以后趋于定值,影响金属管膨胀角和径向膨胀速度的最大因素是炸药与金属壳体质量比值,其值越大膨胀角和径向膨胀速度越大,且试验值与理论模型、经验公式的理论值基本吻合,说明此方法和结论是可行的,能够用于实践中,但其相对于Gurney公式较为复杂。
1.3 金属加速能力评价指标
金属加速能力是用于衡量各类炸药爆轰后对壳体抛射能力的重要指标,不同炸药金属加速能力不同,金属加速能力的评价指标包括了爆速、爆热、爆压等爆轰参数、格尼速度、圆筒试验壳体破裂后壁速、金属壁不同位移处的能量、单位质量炸药推动管壁产生的动量,驱动压力指数或驱动能量指数等,如表1所示。

表1 金属加速能力评价指标及特点
由表1可看出:
1)金属加速能力可通过破片初速进行表征,而破片初速可由炸药的爆速、爆热、爆压等爆轰参数进行估算。这种方法对于单质炸药比较符合,但对于混合炸药,尤其是含铝炸药,采用单一的炸药爆轰参数作为评价指标往往出现与实际结果相反的结果。例如,爆热高的炸药对金属加速能力不一定强,因为炸药中添加高活性金属粉可以提高爆热,但由于二次反应的迟滞现象,其释放的热量并未能及时贡献给金属的加速过程,壳体就已经破裂,加速过程结束。因此,对混合炸药来说,如果弹体是薄壁结构,单独用爆热的大小作为衡量炸药对金属加速能力的强弱,就会出现爆热大而初速小的矛盾现象。同样地,爆速高的炸药其金属加速能力也不一定强,因为单纯的高爆速炸药其猛度较强,炸药爆炸时容易对壳体产生变形和粉碎,爆轰气体产物及早泄露,缩短了膨胀加载历程,金属加速能力反而降低。
2)格尼速度是评估炸药对金属的加速能力的重要参数,适用于对称三明治结构、圆柱体结构、球体结构3种模型。利用格尼速度来计算炸药的金属加速能力,可以消除采用单一爆轰参数评价时出现的矛盾现象,且不限于弹药结构,只要装填比满足0.06≤C/M≤5.6,即可推广至对类似结构下炸药爆轰后金属加速能力的计算,能够比较完善的衡量各类炸药对金属的加速能力,当考虑端面稀疏波时格尼公式需要加以修正。
3)将圆筒试验中壳体膨胀破裂处的壁速、金属壁位移6 mm或19 mm处的能量、金属壁位移处的能量、单位质量炸药推动管壁产生的动量作为金属加速能力的评价指标,这些参量均为基于标准的圆筒试验获得的,是推导格尼速度时的过程量,能够准确比较不同炸药的金属加速能力。但当装药结构尺寸发生变化时,壳体破裂半径随之发生改变,相应地这些参量值将发生变化,基于圆筒试验获得的结果缺乏某种转换关系用以评价其余结构尺寸时的金属加速能力。
4)王新颖等基于瞬时爆轰假定并把多方指数型状态方程或JWL状态方程作为等熵状态方程进行处理,建立了理想炸药爆轰驱动金属加速能力的驱动压力模型和驱动能量模型,并根据炸药理想爆轰的C-J理论和ZND模型计算出爆轰参数,进而计算出驱动压力和驱动能量,并以TNT炸药为基准,提出了驱动压力指数和驱动能量指数用于表征炸药的爆轰驱动金属加速能力。但仅适用于评估理想炸药理想爆轰的情况,非理想炸药是不适用的。
因此,综合分析目前现有的金属加速能力评价指标,认为格尼速度仍然是适用性更广准确性更高的指标参数。
2 格尼速度计算方法
炸药格尼速度是Gurney模型预测破片初速的关键参数,格尼速度需要通过圆筒试验获得,但实际过程不可能每研制一种炸药就开展圆筒试验来确定其金属加速能力,会增加研制成本。因此,国内外许多学者在大量深入研究的基础上,建立了一些近似模型,提出了诸多用于确定格尼速度的经验或半经验的计算方法,下面从以Hardesty & Kennedy为代表的法、以Roth为代表的法、以Keshavarz为代表的组分法进行分析。
2.1 以Hardesty & Kennedy为代表的φ法
是表示炸药组成及能量贮备的示性值,由Kamlet等提出用于计算炸药爆压及爆速的参量,其表达式为:

(1)
式中:为每克炸药所产生的爆炸气体产物的摩尔数;为1 mol爆轰气体产物的平均摩尔量;为炸药爆热。
基于此参量,Hardesty & Kennedy采用最小二乘法拟合得出炸药格尼速度与的关系:
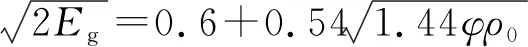
(2)
式中:为炸药密度,经过几种典型炸药验证其误差控制在5%以内。
Kamlet等从另外途径推导出了一种新的格尼速度与的关系:

(3)
与Hardesty & Kennedy法计算结果相比平均误差不超过20 m/s。式(2)和式(3)在求解时,均假设爆轰产物主要由N、C、HO、CO组成,但实际上爆轰产物种类极为复杂,Keshavarz对爆轰气体产物组成进行了重新分析,认为CHNO系列炸药爆轰后按照含氧量优先形成N、CO、HO、CO、O等气体,相应的发生了变化,然后依据试验结果拟合出炸药格尼速度计算公式:

(4)
其相对于式(2)和式(3)准确性有所提高。
同时,根据Kamlet & Finger公式,Locking将其换算为国际单位制,并依据文献[15]中与爆压(或爆速)关系,建立了炸药格尼速度与爆压(或爆速)、密度的关系:
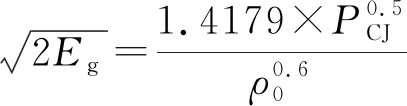
(5)

(6)
式中:为爆压;为爆速。
基于法建立的格尼速度公式对于CHNO系列炸药计算精度较高,但前提是必须知道炸药爆轰产物的具体组分及数量,由于目前工程上采用的炸药大多数为含铝混合炸药,其配方成分较CHNO系列炸药更为复杂,因此如何准确判断产物成分是应用的关键。
张厚生在20世纪80年代也提出了炸药示性值作为能量输出指标,其是指单位体积炸药的爆热和单位体积炸药的爆容的乘积,即:

(7)
式中:为炸药示性值;为炸药爆容。
与国外学者研究得出的值相比,本质上是相同的,均体现的是炸药爆热、爆容两个参数。从示性值的量纲来看,它与单位体积炸药的能量有关,格尼速度与示性值关系式如下:

(8)
综上所述,以示性值或示性值推导的格尼速度计算公式可反映出金属加速能力与炸药爆热、爆容及密度相关,也反应了采用单一爆轰参数作为评价金属加速能力是存在局限性的。
2.2 以Roth为代表的γ法
炸药的绝热指数是爆轰产物体积和温度的函数,与炸药的成分和密度有关。目前,绝热指数直接测量比较困难,通常是间接测定的,Locking提出了两种计算方法,一种是基于炸药稳定爆轰下律状态方程推导的,其仅与炸药密度相关,另一种是根据冲击波理论得出的,其与炸药的爆速、爆压及密度相关。
国内外开展了格尼速度与绝热指数的关系研究,Roth综合考虑格尼公式及气体动力学模型公式,导出了格尼速度与爆速、绝热指数的关系:
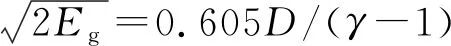
(9)
Koch根据能量守恒定律,推导出任意时刻壳体的速度,同时依据冲击理论,得出格尼速度计算公式:
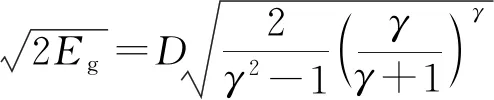
(10)
假设=3,最终简化成格尼速度与爆速的关系,其与Cooper推导的格尼公式基本一致。沈飞等根据圆筒试验炸药爆轰膨胀模型和爆轰产物的律状态方程,得出了与Koch相同的炸药格尼速度表达式。实际上,值并不是恒定的,不同的炸药具有不同的值,即使同种炸药在整个爆轰膨胀阶段也是变化的,其在C-J处最大,而后逐步降低,直至成为理想气体,一般介于1.3~3.0之间。因此,Koch作出的假设缺乏合理性。
Locking等根据公开的圆筒试验结果拟合出一种格尼速度经验公式:
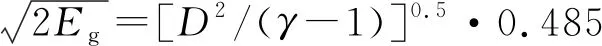
(11)
与试验值进行比较,整体上计算的平均误差和均方根偏差都较小,但含铝炸药计算误差较大。Dany利用BKW程序获得炸药的爆压和绝热指数,提出了炸药格尼速度经验公式:

(12)
由式(12)计算了27种炸药的格尼速度,结果表明对于不含铝炸药而言,均方根偏差为0.04 km/s,对于含铝炸药,偏差为0.05 km/s。因此,该公式适用于任何密度下单质炸药、混合炸药及含铝炸药。
由于多方指数是爆容和爆温的函数,而爆温与爆热基本呈正相关,同时以推导的计算公式基本都包含了爆速这一参数,因此可以看出金属加速能力与爆速、爆容和爆热3个爆轰参数密切相关。
2.3 以Keshavarz为代表组分法
当炸药配方确定后,其密度、氧平衡、生成热、爆轰参数等性能是一定的,对外金属加速作功能力也将确定。因此,利用炸药化学组分直接计算格尼速度是可行的。
Keshavarz根据CHNO炸药的组成元素、装填密度和凝聚相或气相生成热,建立了炸药的格尼速度公式,两种表达式如下:

(13)

(14)
式中:为分子质量;Δ为生成热,其相对于法最大的优势在于不需要知道炸药爆轰产物组成,也不用考虑分子结构中的化学键。Keshavarz又建立了一种更为简单的格尼速度公式,仅依靠炸药密度、氮原子数、氧碳比、氢氧比即可,但前提是氢原子数不能为0,计算公式为:
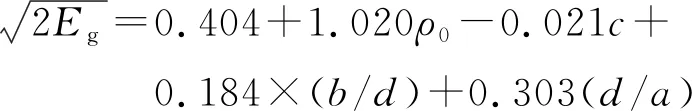
(15)
Keshavarz提出的两种方法计算误差与文献[16-17]基本一致,与某些炸药格尼速度试验值对比其均方根偏差仅为0.04 km/s。式(13)~式(15)在推导过程中参数拟合基于的均为理想炸药试验结果,所以其不适用于计算非理想炸药。
Dany利用装药密度、炸药生成热、C/N/O三种原子数以及分子质量计算出炸药板痕深度,进而计算出了格尼速度,之后又建立了炸药格尼速度与氧平衡、装药密度的相互关系,经过与24种炸药的格尼速度试验值比较,除六硝基茋、塔考特外其余炸药计算误差均控制在4%以内。由于氧平衡中不涉及Al原子个数,因此该经验公式不适用于含铝炸药,且公式拟合过程采用的均为负氧平衡炸药,所以也不适用于零氧平衡和正氧平衡炸药。
考虑到铝粉在炸药爆轰时二次反应对金属驱动的影响,Dany运用多元回归方法建立了用于估算含铝和非含铝炸药的格尼速度,表达式为:

(16)
式中:Δ为燃烧热;和为调节因子。该模型在预测Gurney速度方面相对准确,与Cooper、Locking、Dany、Keshavarz相比,非含铝炸药计算标准偏差基本一致,且可以计算含铝炸药。
2.4 各种方法对比及分析
Locking对法、法进行了评估,将计算值与试验数据进行比较,从平均误差、标准偏差等方面给出了各种方法评估的准确性及适用范围,但评估结果与文献[27]存在部分矛盾现象,我们将所有报道的格尼速度公式计算数据进行重新汇总、整理、对比分析后,得出以下结论:
1)复杂的方法不一定给出更准确的预测结果,例如Hardesty & Kennedy,Kamlet & Finger利用值建立的格尼速度关系式虽然可以评估非铝炸药,但由于计算过程没有考虑铝的存在,对于含铝炸药是不适用的,而利用与爆压(或爆速)关系建立的格尼速度与爆压(或爆速)简单关系式,则适用于含铝炸药的计算;
2)Roth、Koch及Cooper等建立的方法最为简单,但计算较为粗略精度值较低,且不适用于含铝炸药,工程上可以对非铝炸药格尼速度进行初步估算;
3)以Keshavarz为代表组分法最大的优势在于不需做任何假设,仅依据炸药自身结构组成即可完成对格尼速度的计算,但对新研制炸药的计算精度不够,主要原因是在拟合参数过程中基于的试验数据样本量不足,因此其适用范围可能受限;
4)由于目前公开报道的炸药格尼速度试验数据有限,统计分析误差对获得的结果可能影响较大,这也是部分方法在计算炸药格尼速度时误差大的主要原因。因此,在利用试验数据拟合经验公式过程中应考虑样本量的影响。
3 影响格尼速度的因素
上述所有格尼速度的计算方法均未涉及壳体材质的影响,实际上格尼速度不仅与炸药自身性能有关,而且也与金属壳体性质密切相关,因为其对爆轰产物膨胀过程具有重要的影响。以下主要从炸药组分及性能、壳体材质及壁厚两个方面分析格尼速度的影响因素。
3.1 炸药组分及性能
炸药装药是驱动金属壳体高速飞行的能量来源,单位质量炸药所产生的气体体积和对介质破坏力的综合效果越大,对金属加速能力就越强。金属加速能力主要与炸药爆炸总能量,能量释放速率,爆轰气体产物量有关。只有这3个参数具有最佳的匹配性时,金属加速能力才会最强,单纯的追求某一参数极限值的措施是不可取的。
炸药中加入金属铝粉可以提高炸药的爆炸总能量,其作用主要表现为:爆轰时,铝粉与炸药中的氧发生剧烈的反应;与爆轰气体产物CO、HO等反应,并维持长时间的高压;与N发生反应形成氮化物。根据能量守恒定律,炸药的爆热愈高,炸药的加速金属能力应当愈强,实验结果与此有一定的差别,两者的顺序并不完全一致,沈飞等用圆筒试验研究了0%~40%铝含量对RDX基含铝炸药驱动能力的影响规律,结果表明:随着铝粉含量的增加,炸药爆速降低,爆热增加,圆筒壁膨胀到最大速度值所需要的时间逐渐增大,炸药的格尼能和格尼速度均降低。这是由于炸药的能量释放速率不同所致,相对于主体炸药爆炸分解,铝氧化的时间比单质炸药的分解时间长得多,其能量释放的延迟会降低转化为金属动能的转换率,因此真正用于推动管壁的那部分能量比较少,只有当时间足够长时,炸药的全部能量才可能用来推动管壁作功。
因此,提高铝粉在爆炸气体产物膨胀阶段的能量释放速率是提升金属加速能力的关键。Gogulya等研究表明如果主炸药具有较高的负氧平衡,或者含有大量的氢原子,则通过采用纳米含铝混合材料可以提高铝粉在能量释放速率,进而增强含铝炸药的金属加速能力。袁建飞等通过增加硝酸酯化合物改变RDX基含铝炸药的铝氧比,使铝粉反应更加充分,延长爆轰产物膨胀力在中后期的金属加速能力,提高了金属加速能力。同时,硝酸酯物质含氮量都比较高,特别丁三醇三硝酸酯的含氮量高达17%,爆炸后能放出热量及增加大量的氮气、一氧化碳等气体产物,即增加了炸药的爆容,一定程度上也提高了炸药的金属加速能力。熊贤锋等研究表明加入铝粉会降低初始筒壁速度,但随着时间的增加,铝粉后燃效应使产生的气体膨胀作功对金属起到持续加速的作用,会使筒壁速度增加更快,从而起到增加金属加速作功能力的作用。
气态产物是炸药爆炸作功的工质,气态产物越多,爆炸反应热转变为机械功的效率越高,对壳体金属加速能力越强。因此,炸药爆容是体现金属加速能力的重要示性数。王克强基于量子力学原理和化学动力学,研究了炸药分子结构与能量释放速率及金属加速能力的相互关系,将炸药分为共轭炸药和非共轭炸药,其中共轭炸药在冲击波作用下化学键同时断裂,形成的分子碎片多,爆轰气体产物多,能量释放速率快,金属加速能力强。
3.2 壳体材质及壁厚
格尼速度是基于无氧铜特定的结构获得的,然后用此计算相同炸药不同壳体结构下的破片初速,但经试验验证及相关数据分析,格尼速度对于某种炸药而言并不是固定不变的,其与壳体材质、壁厚、动态力学性能有密切的关系。利用标准圆筒试验获得的格尼速度只是一种特定情况下的典型值,在用来评价其余壳体装药下破片速度时需要考虑壳体的影响程度。
壳体的影响首先反映在材料塑性变形方面。王新颖等考虑了圆筒材质对炸药格尼速度的影响,认为在炸药驱动金属系统中,圆筒约束爆轰产物的膨胀过程,不同材料圆筒由于力学性能的不同,在相同的驱动能力下,其破裂半径和破裂时爆轰产物的相对比容存在差异。其中材质强度越大,塑性越好,其膨胀破裂半径越大,爆轰产物的相对比容越大,格尼速度越大,加速能力越强。经过试验研究得出:无氧铜、45#钢、6061铝合金膨胀破裂半径分别为56.5 mm、50.8 mm、53.3 mm。陈醇等采用超高速摄影技术拍摄3种弹体材料壳体膨胀破碎过程,相比50SiMnVB 钢壳体和40CrMnSiB 钢壳体,30CrMnSiNi2A 钢壳体形成破片的最大初速分别提高了31.9%和19.0%,这是由于30CrMnSiNi2A 钢的极限抗拉强度明显高于50SiMnVB 钢和40CrMnSiB 钢,这减少了壳体提前破碎而造成的能量泄露,使材料断裂的时刻更加逼近炸药爆轰能量充分释放的时刻。范亚夫等研究表明将TC4壳体经过双重退火处理后,强度稍降,但塑性和断裂韧性提高,这种改变使圆筒在爆轰过程中爆轰产物未泄漏之前能够充分膨胀,壳体破碎时间推迟,断裂时壳体膨胀速度增加。因此,柱壳爆轰驱动的强度效应不容忽略,壳体力学特性对于膨胀及破裂过程具有重要影响,而壳体力学特性可通过不同热处理工艺获得。
同时,壳体壁厚、面密度等性能与格尼速度密切相关,Joseph等研究表明壳体壁厚增加,格尼速度降低,相同壳体壁厚条件下,壳体为钢时格尼速度明显低于铜或铝,相同面密度条件下,壳体为铜时格尼速度要高于钢或铝。如图3、图4所示,分别给出了炸药格尼速度与壳体壁厚、面密度的关系。

图3 格尼速度与壳体壁厚的关系

图4 格尼速度与壳体面密度的关系
同时,Backofen建立了壳体壁厚、密度与格尼速度的经验关系式。
目前大部分弹药结构并不是标准圆筒试验中规定的装药尺寸结构和壳体材料及厚度,特别是目前防空反导弹药大多采用的是半预制或全预制型壳体结构,且壳体材质一般为低碳钢或硬铝合金,其在炸药爆轰加载下破片体膨胀半径相对无氧铜要小,爆轰气体产物膨胀加载历程短,采用格尼速度计算的破片初速与实际值可能存在偏差。因此,在弹药设计中要综合考虑炸药装药和壳体的匹配性。
4 结论
文中简要分析了炸药爆轰加载金属壳体的3个阶段、理论计算方法、评价指标,重点总结并对比了目前格尼速度的3类理论经验计算方法,讨论了其优缺点,并分析了格尼速度的影响因素,主要结论如下:
1)从炸药爆轰、壳体膨胀破裂到高速驱动整个加载过程来看,金属壳体加速能力包括3个阶段:炸药爆轰波瞬时加载阶段、爆轰气体产物膨胀加载阶段、壳体破裂后爆轰气体产物的二次持续加载阶段,格尼速度是金属加速能力重要评价指标,其反映的是金属加速过程爆轰气体产物二次持续加载后的最终速度。
2)目前报道的各种格尼速度计算方法精度、适用范围均存在差异,使用过程应慎重选择,且针对的主要是单质炸药和理想混合炸药,仅部分涉及非理想含铝炸药,计算精度较低,这是由于含铝炸药铝粉在C-J界面上反应速率低,其爆轰性能相对于理想炸药明显不同,考虑到目前工程上含铝炸药的广泛应用,建立含铝炸药的格尼速度计算方法是未来的研究方向。
3)格尼速度受到炸药自身性能和壳体材质两方面的影响,壳体材质主要通过影响爆轰气体产品膨胀阶段影响金属加速能力,格尼速度是基于标准的圆筒试验获得的,不同的圆筒试验条件下获得的格尼速度是不同的。基于目前弹药壳体采用的大部分为低碳钢或硬合金铝,其性能与无氧铜材质明显不同,因此采用格尼速度来计算弹药破片初速应该说并不是十分准确的。在实际过程中,应适当考虑壳体材质的影响。
