基于半实物仿真的视线角速度估计参数设计

王 冬，刘 琳，陈 韵

(西安现代控制技术研究所，西安 710065)

0 引言

随着捷联制导部件性能的提升以及捷联制导控制技术的发展，自寻的捷联制导技术已经逐渐能够满足现代作战中日益增长的精确打击任务需求。视线角速度估计算法作为激光捷联制导的核心技术之一，对于捷联制导控制系统的设计至关重要。去耦能力强、跟踪速度快是捷联制导视线角速度估计算法的根本要求。

目前，国内外学者对捷联制导技术的研究多集中在视线角速度估计及隔离度影响分析及抑制等技术层面。捷联导引头输出测角信息中包含较大噪声，且探测视场越大噪声越明显，若是采用直接微分的方法则会放大噪声，以至于视线角速度信息被淹没其中，因此非线性滤波估计法是当前估计视线角速度的常用方法。李璟璟等提出了一种基于粒子滤波算法捷联导引头视线角速率估计方法。王佩等采用跟踪微分器(TD)设计了一种全捷联导引头有效制导信息估计方案。

利用光电探测器和惯性导航系统敏感到的信息来解耦计算惯性视线角,再估计视线角速度是捷联制导的基本方案，但并不能像平台导引头一样直接测量视线角速度。当惯性导航系统和光电探测器存在刻度尺误差、量测噪声以及输出延时不一致等特性时，惯性视线角和视线角速度信息中将耦合有弹体姿态运动信息，从而形成隔离度寄生回路，影响制导回路稳定性。相较于平台导引头末制导方式，捷联制导的隔离度问题也十分突出。一般用隔离度指标来评价导引头隔离弹体扰动的能力。隔离度指标的简单标量计算方法为弹目相对运动关系不变时导引头输出视线角速度的峰峰值与弹体姿态角速率峰峰值的比值。田源等推导出了描述捷联制导视线角速度隔离度的公式，并研究了隔离度影响制导回路的原理，设计了滤波器对隔离度寄生回路进行滤波，从而改变导引头和惯性导航系统量测信息传输通路的时间频率特性，使其趋于一致，抑制干扰噪声。李富贵等、袁亦方等分析了捷联导引头隔离度寄生回路产生的原因，通过对比例导引法平面制导模型进行研究，分析了导引头动态特性、延时和剩余制导时间对隔离度寄生回路的作用方式。王伟等研究了捷联导引头的隔离度成因之一延迟作用，得出了当探测器测量的体视角线存在纯延迟环节时，隔离度将受到严重影响的结论，弹体的气动时间常数的减小能够缓解该问题。

以上研究对捷联制导隔离度问题产生的机理研究较充分，但对抑制隔离度问题的方法研究不够或工程实现较困难。文中主要设计了一种工程上应用较简便的捷联制导视线角速度估计算法，并针对激光捷联制导设计中经常遇到的解耦效果不理想以及提取视线角速度的隔离度较差等问题,提出了制导部件时间同步算法以及基于半实物仿真的参数设计方法加以解决。

1 视线角速度估计

捷联制导视线角速度估计通常包括将捷联导引头输出的弹体系视线角通过解耦转化为惯性系下的视线角和对惯性系下的视线角进行微分滤波获取视线角速度两个过程。

弹体系视线角与惯性系视线角在二维平面内的几何关系如图1所示。

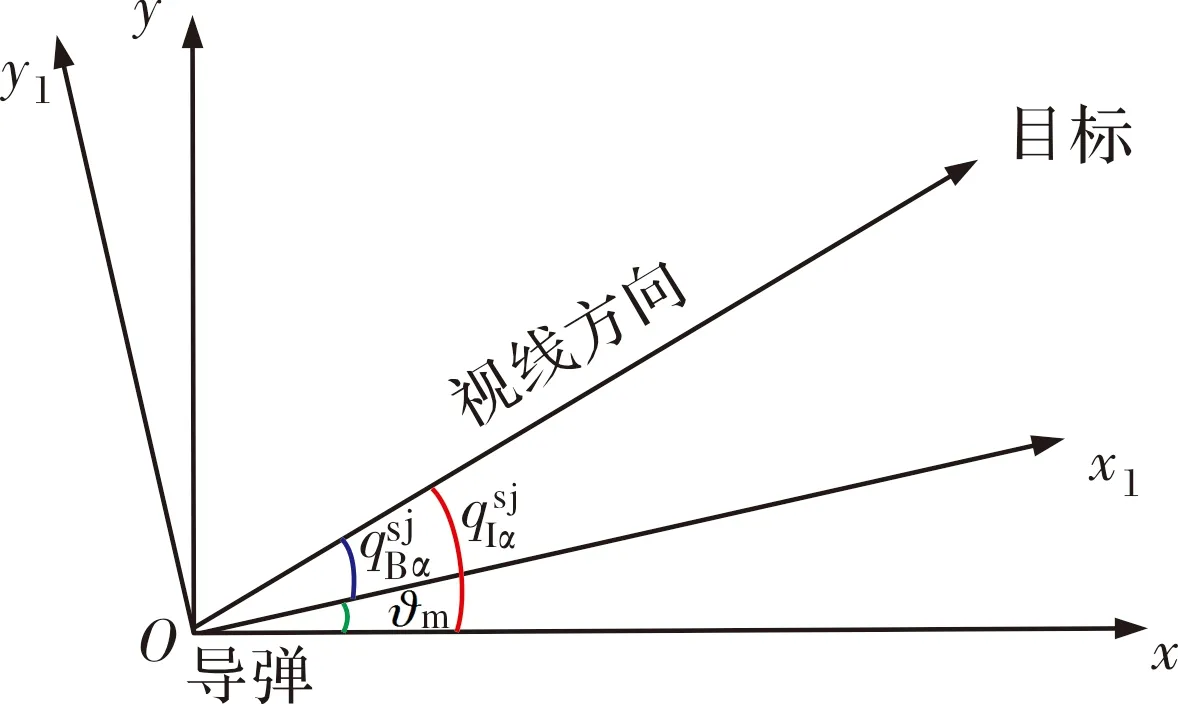
图1 弹体系视线角与惯性系视线角几何关系

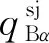
通过弹体坐标系到惯性坐标系的转换可得到视线角的解耦算法：

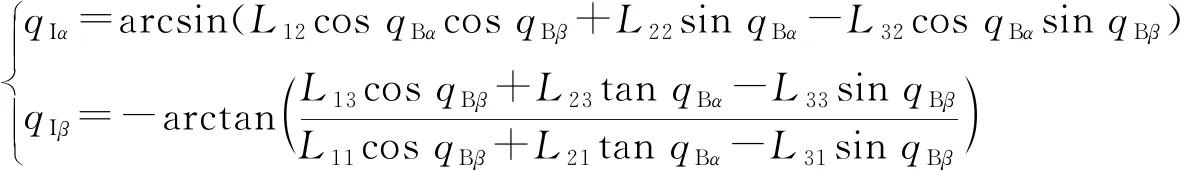
(1)

式中:I和I分别为解耦到惯性系下的俯仰视线角和偏航视线角；B和B分别为捷联导引头测量的弹体系下的俯仰视线角和偏航视线角。

转换矩阵可表示为：

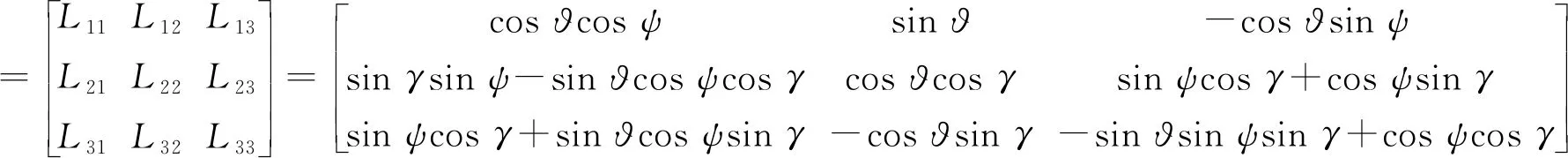
(2)

式中:ϑ、、分别为惯性导航系统测量的弹体的俯仰、偏航和滚转姿态角。

激光捷联导引头因测角线性区较大，所以测角信息中噪声较为明显，经过解耦的惯性系视线角信息中也必然包含噪声信息，采用对惯性系视线角直接微分求取视线角速度的方法会造成噪声放大，甚至会淹没有效的制导信息，因而常用非线性滤波估计法来解算视线角速度。自抗扰控制中提出的非线性跟踪微分器(NLTD)能在对惯性系视线角信息微分的同时对噪声信息进行抑制，可用于视线角速度的估计。

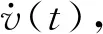
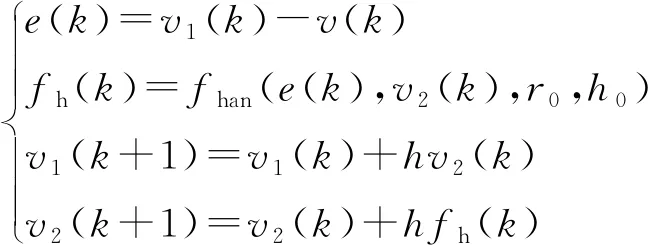
(3)

式中：为采样的周期;、为能够进行调节的参变量。函数(,,,)的算法为：

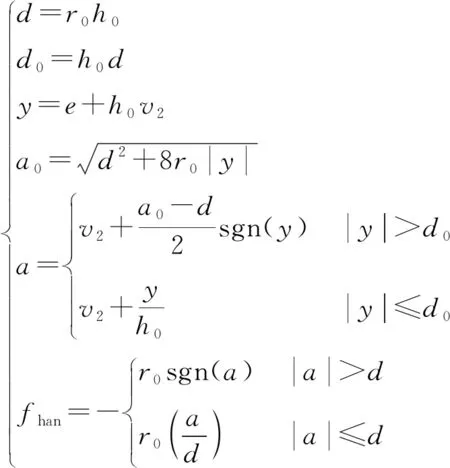
(4)

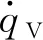
设计NLTD参数、时，使随制导剩余时间线性增大，随制导剩余时间线性减小，从而降低制导末端区视线角速度跟踪动态延迟，保证跟踪快速性，匹配导引律末端区特性，提高捷联制导精度。但该方法会造成末端对噪声干扰滤波效果下降，导致姿态振荡加剧。因此需要从解耦算法上提升制导部件时频特性，保证估计的视线角速度隔离度能够使得寄生回路稳定，不影响末制导精度。

2 隔离度抑制与参数设计方法

理论分析和工程实践都表明捷联制导估计视线角速度的隔离度对制导精度及末制导姿态稳定程度影响较大。式(1)～式(4)所示的解耦算法表明捷联制导利用捷联导引头和惯性导航系统的测量信息构建数学平台来隔离弹体运动，所以全捷联导引头的隔离度代表的是视线角速度估计算法对导引头测角误差、导引头和惯性导航系统的刻度尺误差、动力学误差以及制导信号延时等误差对视线角速度计算影响的抑制能力。文中重点考虑制导信号延时产生隔离度问题的原理并提出抑制该类隔离度问题的方法。

考虑捷联导引头纵向平面内的测角关系，不考虑导引头和惯性导航系统刻度尺误差，捷联导引头体视线角测量值可表示为：

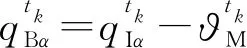
(5)

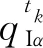
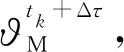
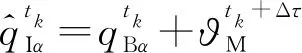
(6)

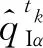
将式(5)代入式(6)可得：

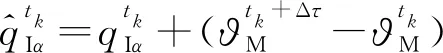
(7)

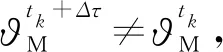
视线角速度估计算法计算过程中导引头数据更新率远远小于惯性导航系统数据更新率，飞控计算机收到捷联导引头有效数据时刻同时采样最新惯性导航系统数据进行解算。此时，从数据生成频率的角度考虑，解算使用的惯性导航系统姿态信号延迟小于等于一个惯性导航系统数据更新周期，文中对此类延迟不进行补偿。

捷联导引头和惯性导航系统从待测量角度发生变化到其输出角度变化之间的延迟为部件固有延迟。当其固有延迟差异较大时，采用式(8)、式(9)的算法进行补偿：

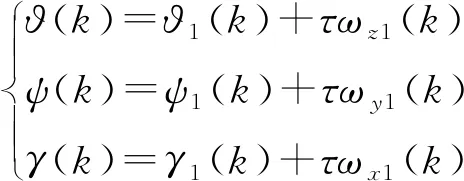
(8)

=-

(9)

式中：ϑ()、()、()为惯性导航系统姿态角;1()、1()、1()为姿态角速度;为惯性导航系统固有延迟;为导引头固有延迟;ϑ()、()、()是经过延迟补偿的弹体姿态角，采用该角度代入式(1)～式(4)进行解耦计算。

式(8)、式(9)所示的惯性导航系统延迟补偿算法对于激光捷联制导视线角速度估计，特别是将体视线角解耦到惯性系视线角的过程至关重要，延迟补偿参数设计的优劣直接影响解耦的效果，最终体现为估计视线角速度的隔离度指标。

在半实物仿真环境下，保持弹目几何相对运动关系不变，即激光目标模拟器输出激光能量信号但是不运动。将惯性导航系统及激光捷联导引头安装在模拟弹体姿态运动的三轴转台上，控制转台俯仰姿态角按照给定幅度和频率规律运动，偏航角、滚转角保持不变。三轴转台和激光目标模拟器模拟的弹目几何相对位置关系进行合理地设置并根据激光捷联导引头测角线性区指标合理设置转台俯仰姿态角摆动幅度，保持转台俯仰姿态运动过程中，激光捷联导引头一直工作在其测角线性区内。

飞行控制器采样惯性导航系统俯仰角信号及激光捷联导引头俯仰体视线角信号，并通过式(1)～式(4)实现解耦计算，输出惯性坐标系俯仰视线角。此时，因为在惯性空间中弹目几何相对运动关系未发生变化(激光目标模拟器未运动)，故惯性坐标系俯仰视线角输出应不发生变化。在实际中，因为部件测量噪声、制导信号时间不同步、刻度尺误差等因素影响，惯性坐标系俯仰视线角输出不会保持不变，可以通过调节延迟补偿参数的大小，使惯性坐标系俯仰视线角输出变化最小，从而消除制导信号时间不同步对解耦的影响，减小估计视线角速度的隔离度，得到品质较好的制导信号。

3 半实物仿真验证

基于半实物仿真的延迟补偿参数的设计方法，分别令延迟补偿参数取±20 ms、±10 ms、±5 ms和0 ms，三轴转台俯仰角运动规律设置为：=5sin (2π)，按前述方法进行半实物仿真试验记录飞行控制器输出。通过分析对比惯性系俯仰视线角和俯仰视线角速度的变化幅值，选择最优的延迟补偿参数。

图2为惯性导航系统俯仰角信号及激光捷联导引头俯仰体视线角信号以及延迟补偿参数=10 ms补偿后的俯仰角。

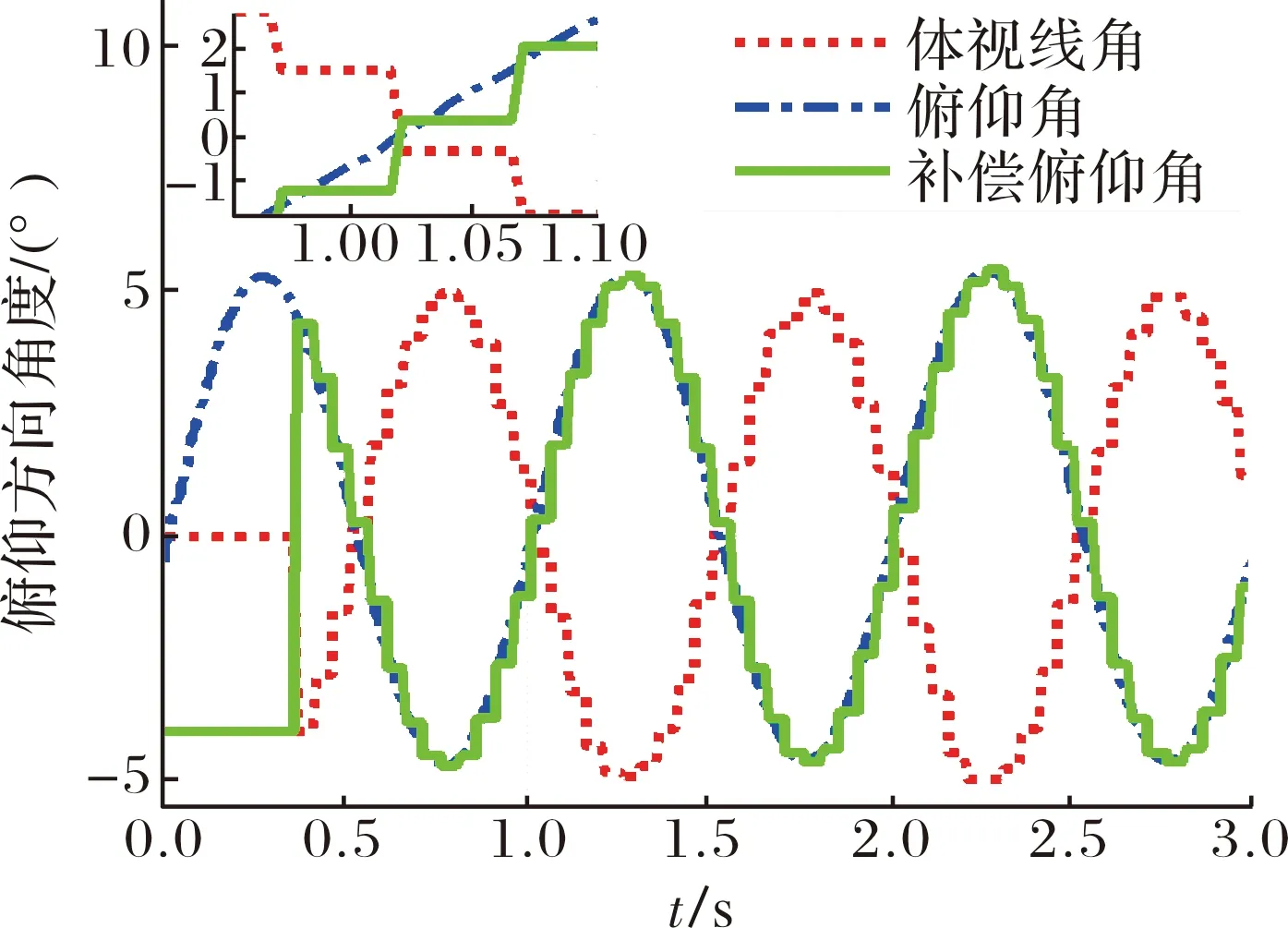
图2 俯仰方向测量值与补偿值角度曲线

由图2可见，补偿后的俯仰角超前于惯性导航系统输出俯仰角且与捷联导引头俯仰体视线角信号完全反向。图3为延迟补偿参数分别取10 ms、±5 ms时，按式(1)～式(4)进行解耦计算，输出的惯性系俯仰视线角，延迟补偿1、2、3分别对应延迟补偿参数取10 ms、5 ms、-5 ms。

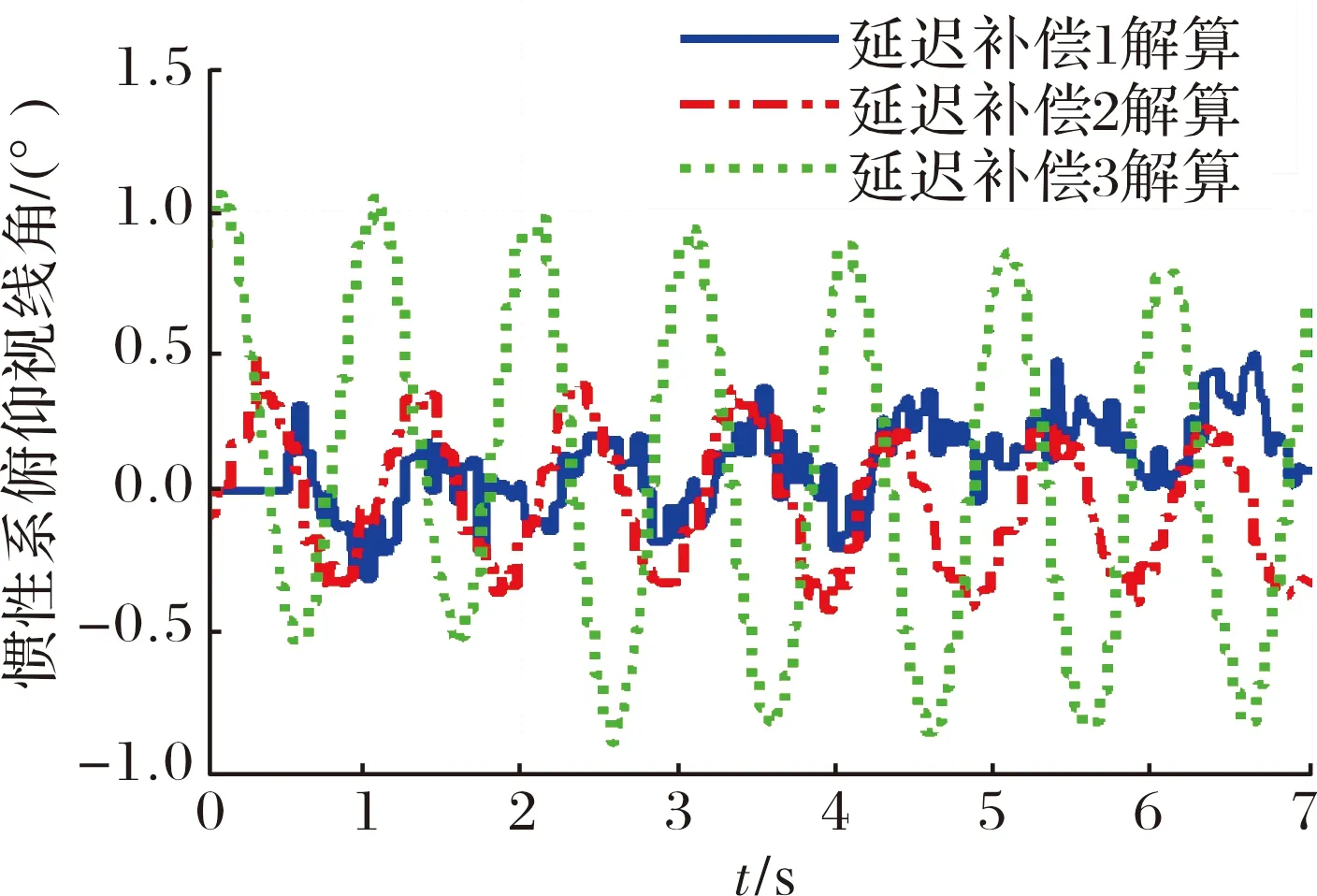
图3 惯性系俯仰视线角对比曲线

由图3可见，延迟补偿1对应的惯性系俯仰视线角的幅值最小，为±0.2°，解耦效果最好，基本达到只抑制制导部件时间不同步带来的隔离度问题的极限。延迟补偿2次之，延迟补偿3解耦效果较差。图4为延迟补偿1、2、3对应的俯仰视线角速度，其估计效果与图3结果一致。

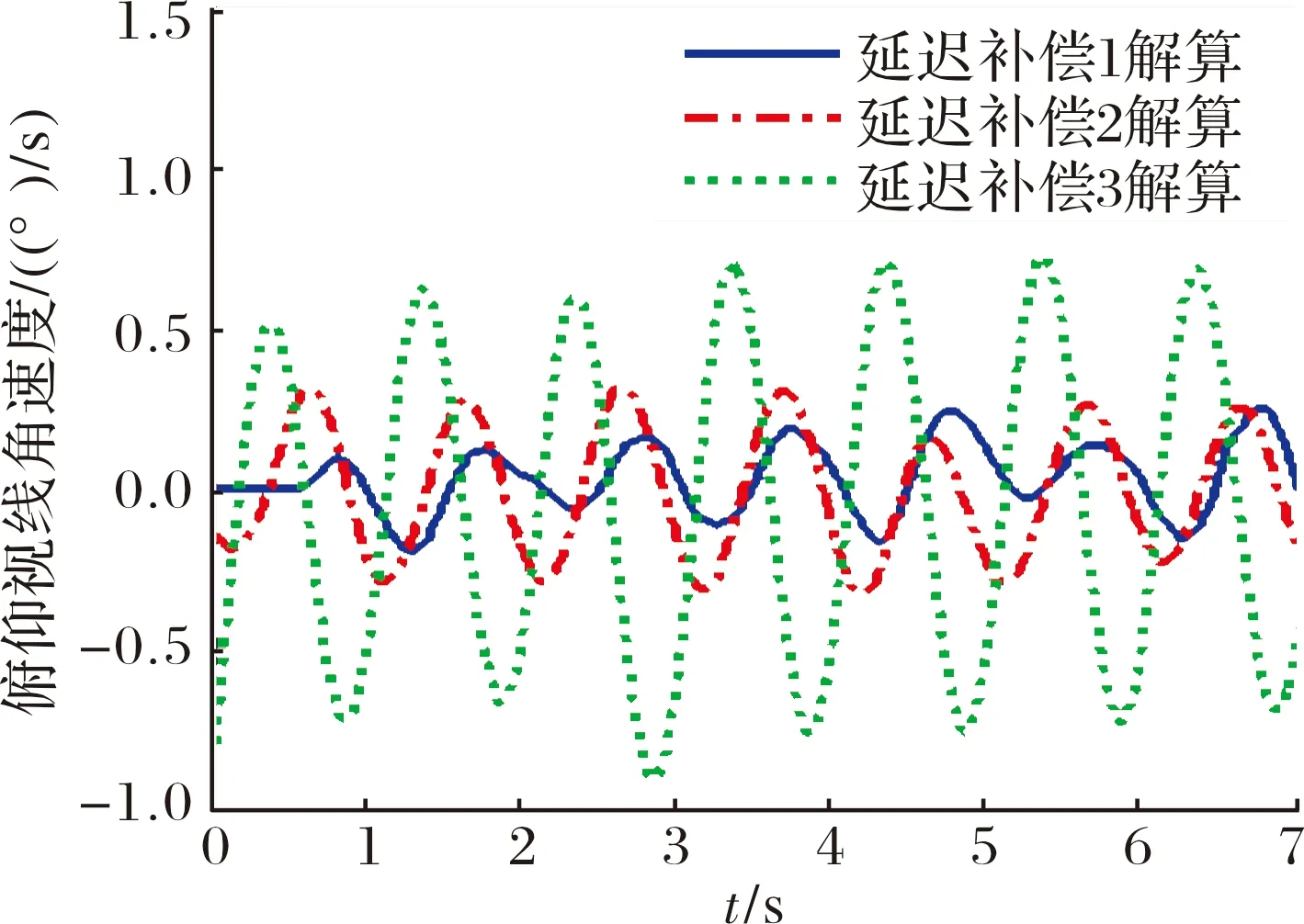
图4 俯仰视线角速度对比曲线

图5为延迟补偿1俯仰视线角速度估计结果与弹体俯仰角速度对比曲线，用于评估估计视线角速度隔离弹体姿态运动的能力。由隔离度定义可计算得到隔离度为0.6%。

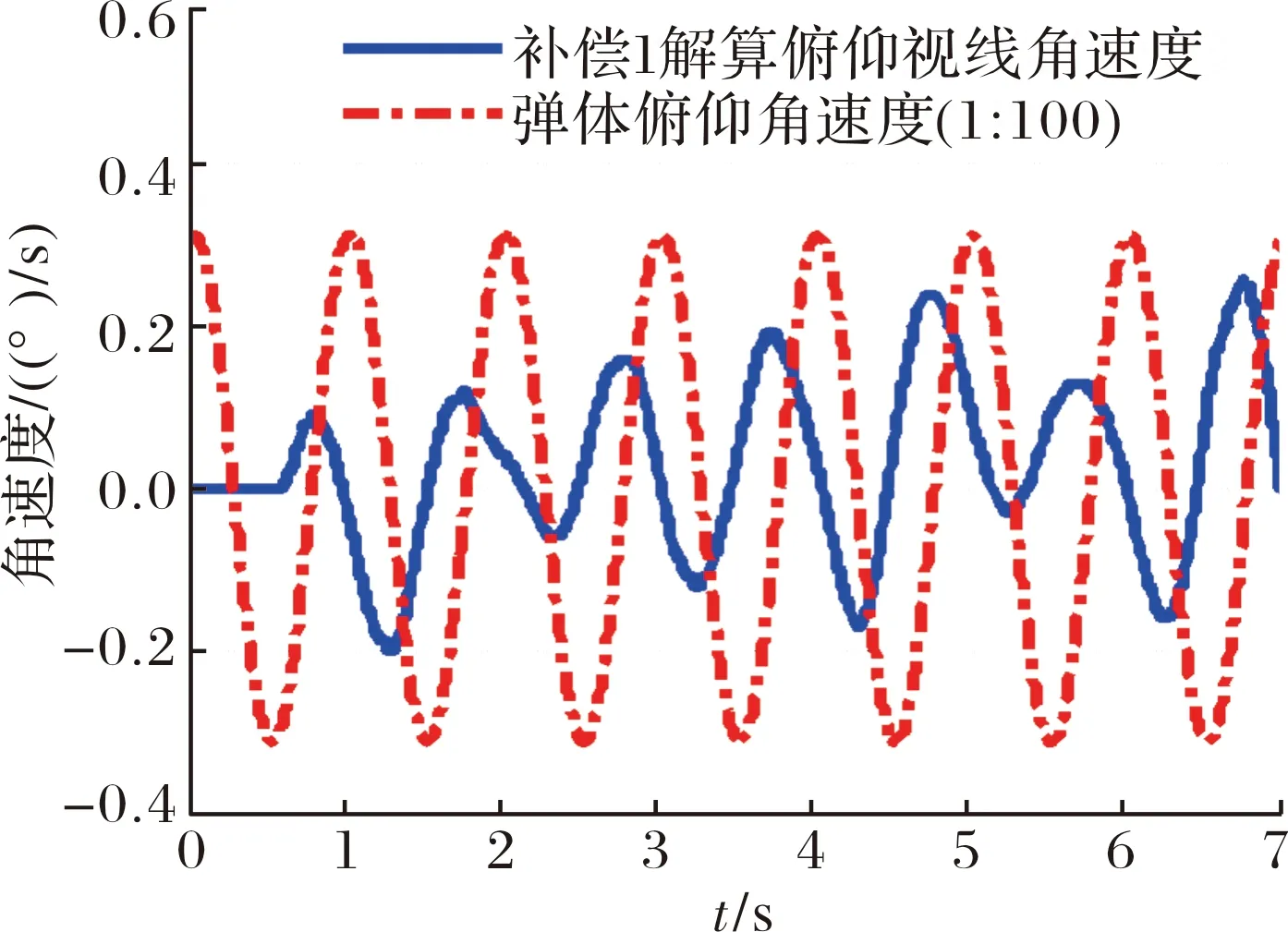
图5 姿态角速度与视线角速度对比曲线

表1为延迟补偿参数分别取10 ms、±5 ms时，惯性系俯仰视线角幅值、俯仰视线角速度幅值和隔离度对比结果。

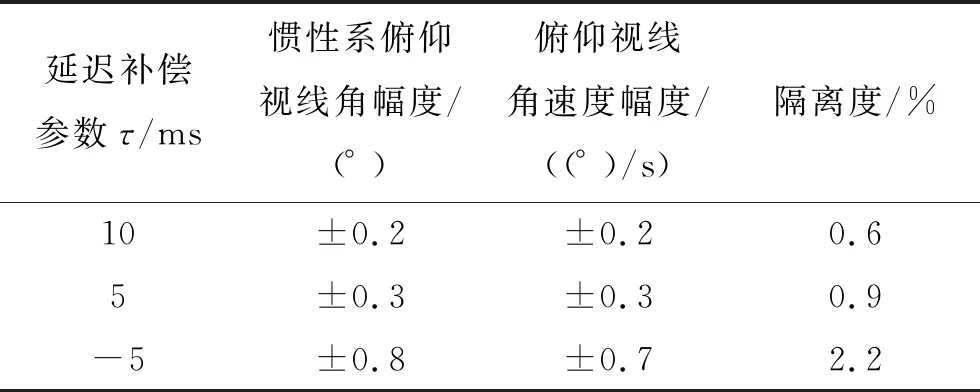
表1 解耦特性仿真结果对比

由表1数据分析可见，延迟补偿参数=10 ms时，捷联制导解耦效果最好，因此设计延迟补偿参数=10 ms进行弹道仿真。

半实物仿真条件为：射程6 000 m，射角6°，海拔高度1 000 m，温度20 ℃。分别进行理想条件和扰动条件下的半实物仿真，仿真得到的惯性导航系统输出俯仰角、捷联导引头输出的俯仰体视线角分别如图6、图7所示。

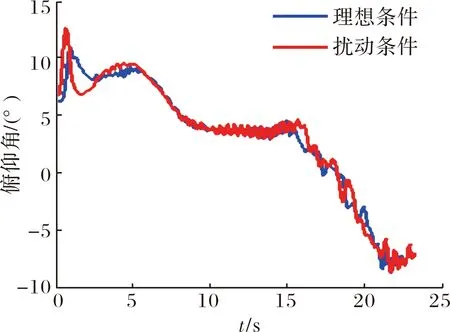
图6 俯仰角曲线

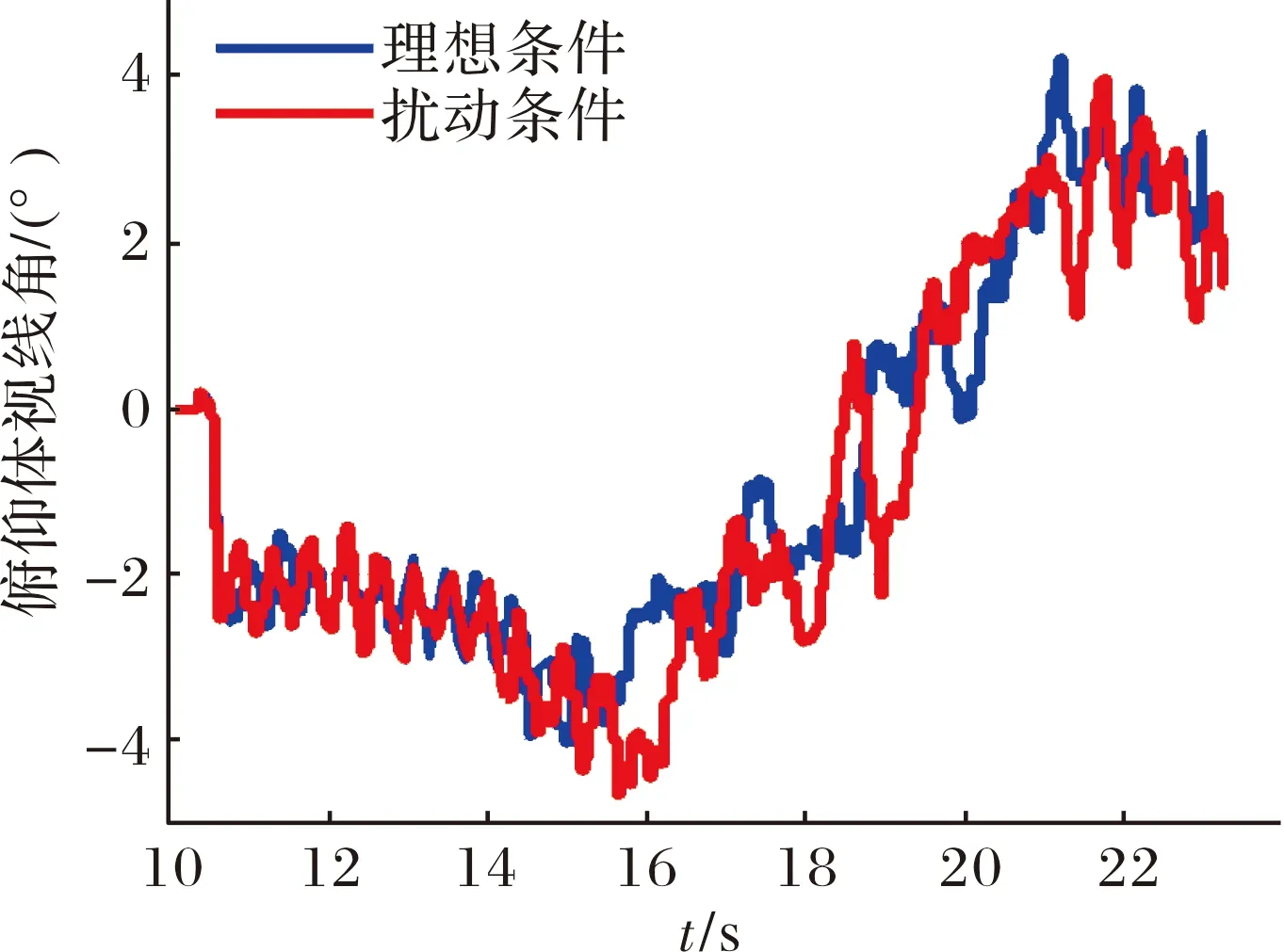
图7 俯仰体视线角曲线

由图6可得，转入末制导后，弹体俯仰角按照比例导引律的作用逐渐下压，且制导过程姿态变化较平稳。由图7的捷联导引头输出俯仰体视线角对比图6的姿态角曲线，可以看出捷联导引头输出包含明显的测角噪声。捷联制导估计的俯仰视线角速度如图8所示。

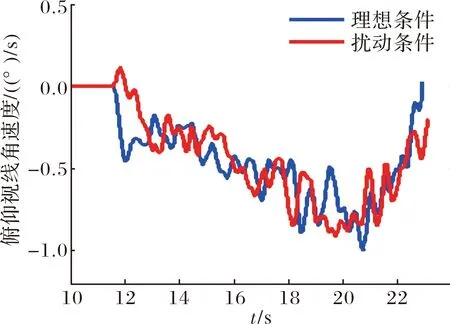
图8 俯仰视线角速度曲线

由图8估计的俯仰视线角速度曲线可见，估计视线角速度较平稳，可用于末制导比例导引控制。

4 结论

设计了一种满足实际应用需求的捷联制导视线角速度估计算法，并针对激光捷联制导设计中经常遇到的解耦效果不理想以及提取视线角速度的隔离度较差等问题提出了制导部件时间同步算法以及基于半实物仿真的参数设计方法进行解决。仿真结果表明，设计的制导部件时间同步算法以及基于半实物仿真的参数设计方法能够很好地抑制提取视线角速度的隔离度，视线角速度估计值用于末制导比例导引后弹体姿态较平稳，末制导特性较好。