一种基于固体火箭发动机的悬浮火箭弹道建模与仿真研究

高 乔，杨 军，李晓晖，张兵峰

(西安航天动力技术研究所，西安 710025)

0 引言

在海面作战环境中，舰船面临着反舰导弹的威胁，早期主要采取硬碰硬的拦截措施来应对，而现在随着反舰导弹的打击性更强，命中精度更高，早期的应对方式已经不再适用，因此将采取软对抗的防御措施，比如采用舷外有/无源干扰的电子干扰手段。

美澳联合研制的空中悬浮火箭型诱饵“Nulka”得到了广泛应用。在20世纪70年代，悬浮火箭的概念开始出现，1981年4月悬浮飞行的原理首次进行了成功的演示，同年5月进行了成功的飞行试验。悬浮火箭是一种具备在空中悬停和慢速移动的特殊火箭，通过悬浮平飞模拟舰船运动的方式诱导反舰导弹，从而保护舰船。同时悬浮火箭按照推进剂类型可以分为液体和固体两类。液体悬浮火箭具备推力随控、工作时间长和能量比高的特点；固体悬浮火箭具备使用维护简单、贮存期长的特点，一般应用于武器领域。

文中以一种基于固体火箭发动机的悬浮火箭为研究对象，依据相关理论经验以及文献资料，在考虑悬浮火箭自身特性，气动特性偏差以及姿态、高度、速度控制回路性能等工程实际约束的条件下开展研究，提出一种控制方案，使悬浮火箭具备悬浮定高横向低速机动飞行等功能。

1 悬浮火箭的方案概述

1.1 方案概述

为了更好地发挥效能，悬浮火箭在完成上升段后，将模拟舰船航行运动，由于航行速度慢，气动力较弱，无法提供火箭飞行所需要的控制力。因此在飞行过程中，需要基于推力矢量式发动机提供飞行所需推力。

悬浮火箭采用大仰角发射方式，发射角度不低于70°，经过发射和上升弹道后，将在一定悬浮高度范围内横向机动飞行，攻角达到45°～90°。

1.2 弹道和控制方案

悬浮火箭从发射到实施干扰整个过程如图1所示，飞行任务剖面分为爬升段、平飞段、下落段3个阶段。

图1 悬浮火箭飞行任务示意图

图2所示为悬浮火箭在飞行过程中的受力示意图，悬浮火箭在推力的作用下起飞，从发射筒发射出去后，进入爬升段；之后在平飞段，气动力、重力、推力和控制力在竖直方向的分力保持相等，当姿态出现紊乱时，对控制力进行调节，从而使悬浮火箭保持一定姿态悬浮定高飞行，在推力结束后，自由下落。

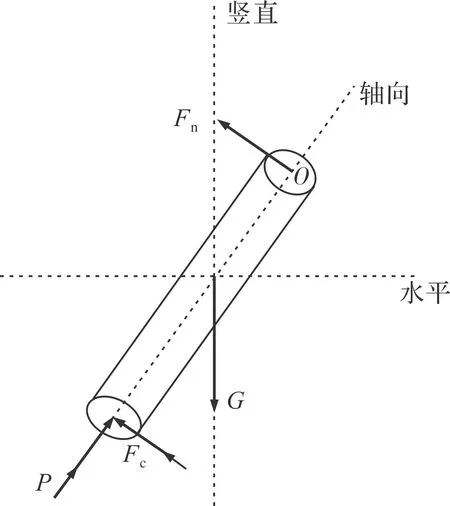
图2 悬浮火箭受力示意图

2 刚体弹道模型建立

2.1 悬浮火箭空气动力模型

、、分别为空气动力在箭体坐标系下的3个分量，其表达式为：

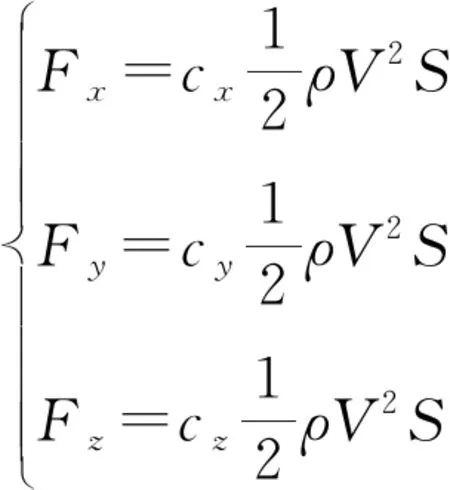
(1)

式中：、、分别为3个方向上的气动力系数;为空气密度;为悬浮火箭飞行速度;为箭体参考面积。

、、分别为气动力矩在箭体坐标系各轴的投影，其计算式为：

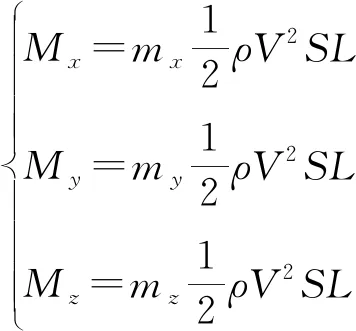
(2)

式中：、、分别为3个坐标轴上的气动力矩系数;为箭体长度。

2.2 悬浮火箭动力学模型

1)质心运动的动力学方程

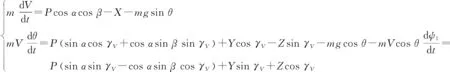
(3)

式中：、、为空气动力在速度坐标系下的分量;为发动机推力;为悬浮火箭质量；为速度倾角斜角；为弹道偏角。

2)绕质心转动的动力学方程

(4)

式中：、、为悬浮火箭对箭体坐标系各轴的转动惯量的投影;、、为箭体坐标系相对于地面坐标系的转动角速度在箭体坐标系各轴的投影。

2.3 悬浮火箭运动学模型

1)质心运动的运动学模型

悬浮火箭的质心运动可以表达为：

(5)

式(5)经过积分可以求出悬浮火箭质心相对地面坐标系原点的位置信息。

2)绕质心转动的运动学方程为

悬浮火箭绕质心转动的运动学方程为：

(6)

2.4 悬浮火箭质量模型

悬浮火箭在飞行过程中，由于固体火箭发动机不断消耗燃料，因此，悬浮火箭的质量是随着时间不断减小的，描述质量变化的微分方程为：

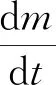
(7)

式中，为单位时间内质量消耗量。

2.5 几何关系模型

描述悬浮火箭运动特性的8个角度参数之间并不是独立的，因此存在如下角度几何关系：

(8)

式中：为攻角;侧滑角;ϑ为俯仰角;为偏航角;为滚转角;为弹道倾角。

3 控制模型的建立

3.1 姿态控制回路

姿态控制采用阻尼回路、姿态回路双回路反馈控制，回路结构图如图3所示，其中姿态角为控制回路，角速度为阻尼回路。

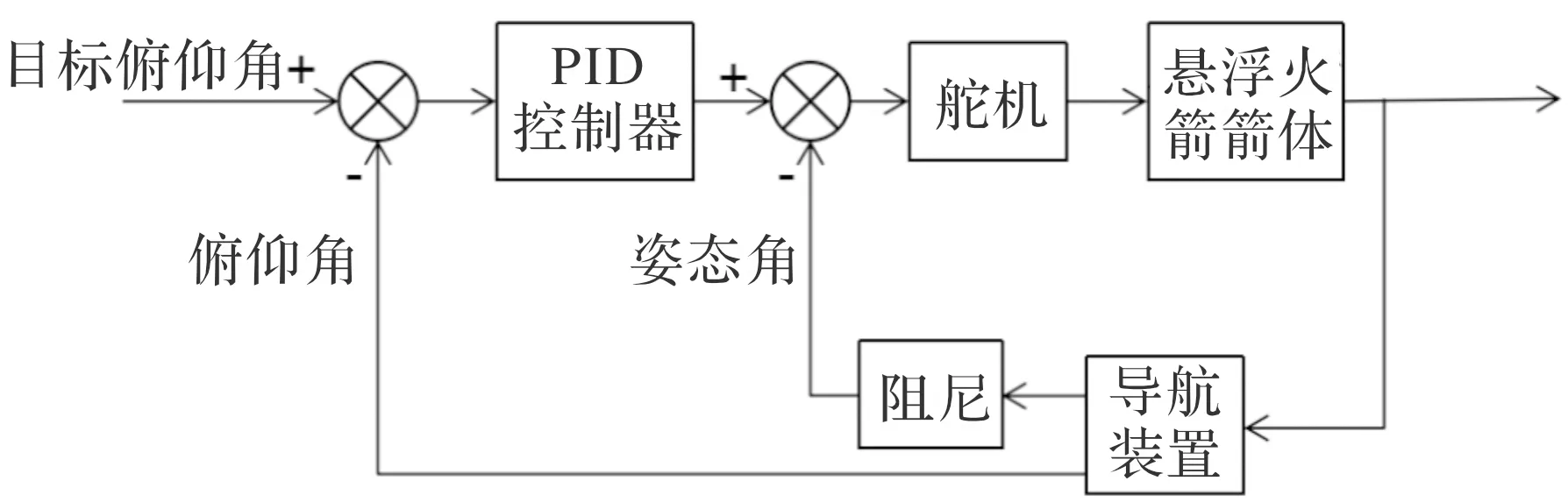
图3 姿态控制回路图

在悬浮火箭的爬升段，为了使悬浮火箭快速飞至目标高度60 m，满足悬浮高度要求，在爬升段控制俯仰角角度变化如表1所示，到达平飞段后，保持悬浮飞行并控制俯仰角在80°左右。

表1 俯仰角角度变化表

3.2 高度控制回路

悬浮火箭高度控制回路采用“高度+速度”的双回路反馈控制，回路图如图4所示，悬浮火箭的飞行高度作为控制回路，高度方向的速度作为阻尼回路。

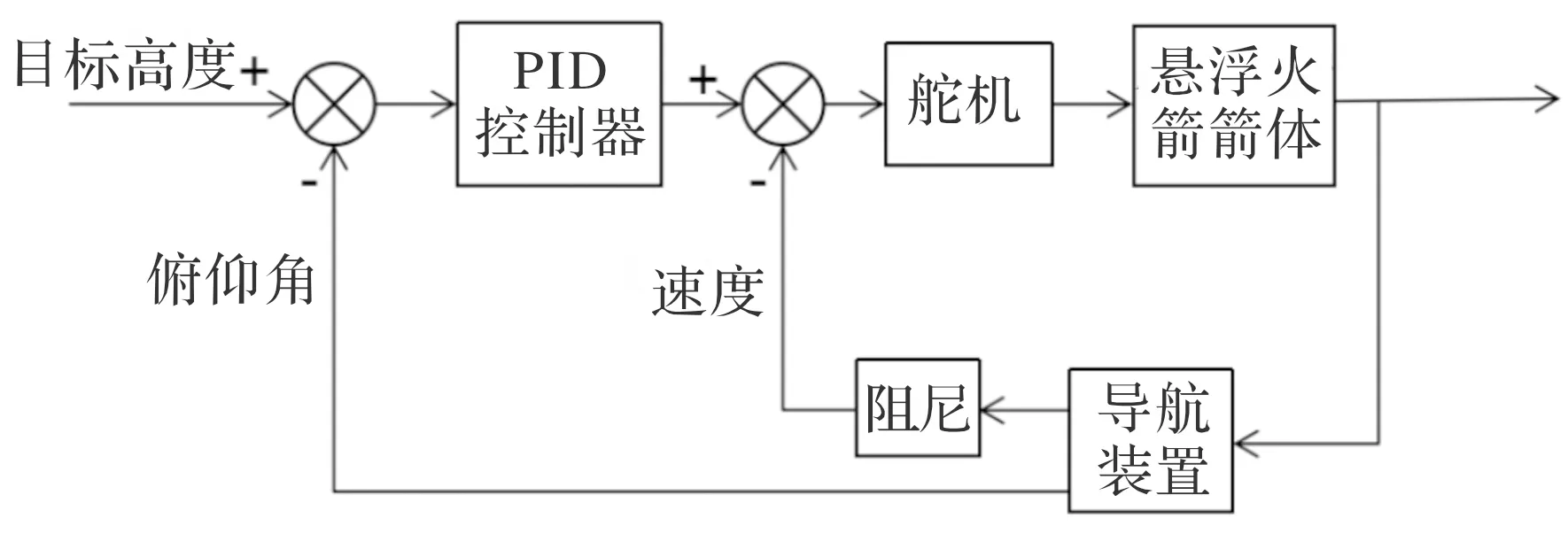
图4 高度控制回路图

控制在5 s时悬浮火箭到达指定的60 m高度，之后控制稳定在这一高度飞行，一段时间后自由坠落。

3.3 速度控制回路

悬浮火箭速度控制回路采用“速度+加速度”的双回路反馈控制，回路结构图如图5所示，悬浮火箭速度为控制回路，相应的加速度作为阻尼回路。

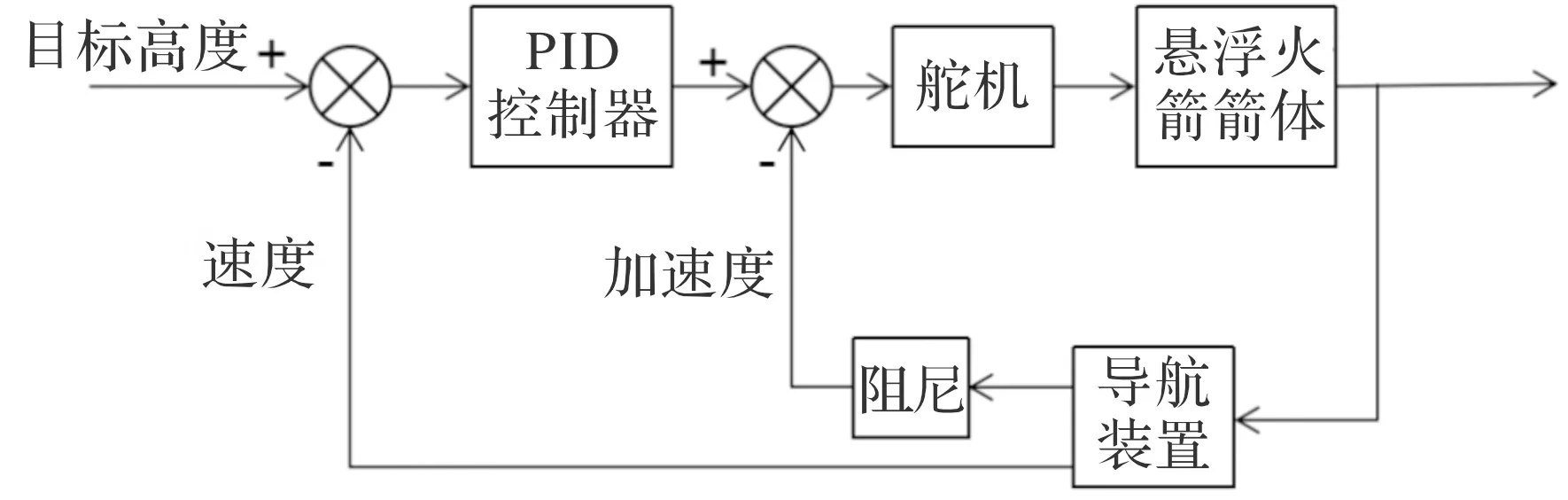
图5 速度控制回路结构图

4 仿真校验

4.1 仿真条件

在箭体坐标系下建立六自由度仿真模型，仿真条件如表2所示。

表2 弹道初始参数

4.2 飞行弹道仿真结果

60 m悬浮高度，25 m/s悬浮飞行速度下的仿真结果如图6～图9所示。

图6 速度随时间的变化曲线

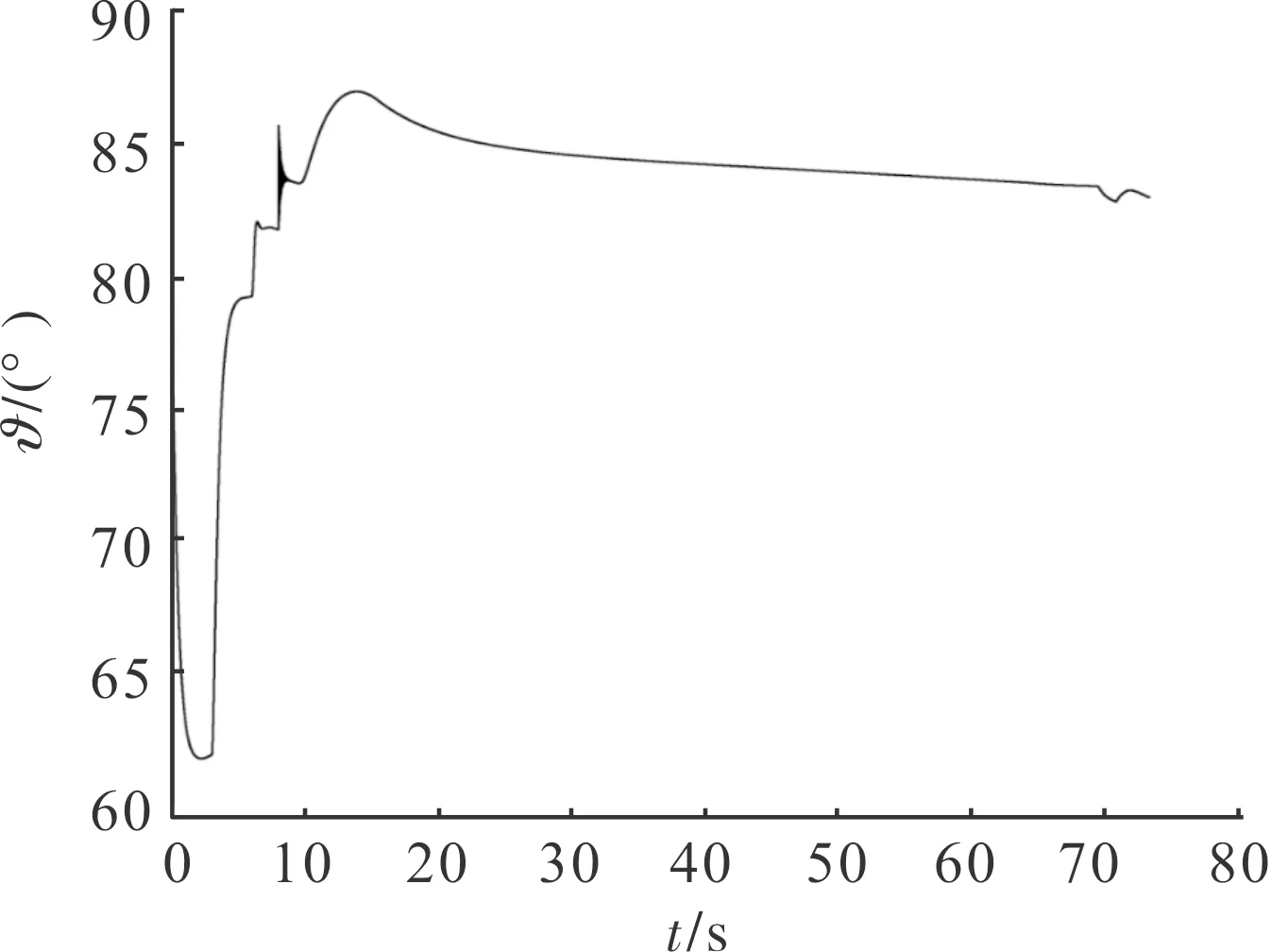
图7 俯仰角随时间的变化曲线

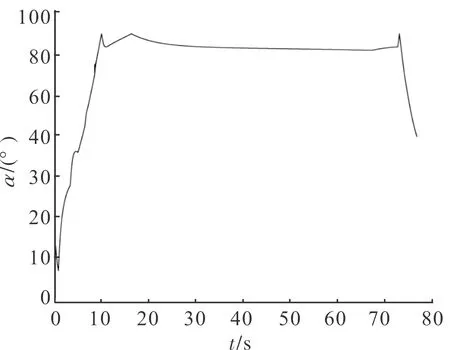
图8 攻角随时间的变化曲线

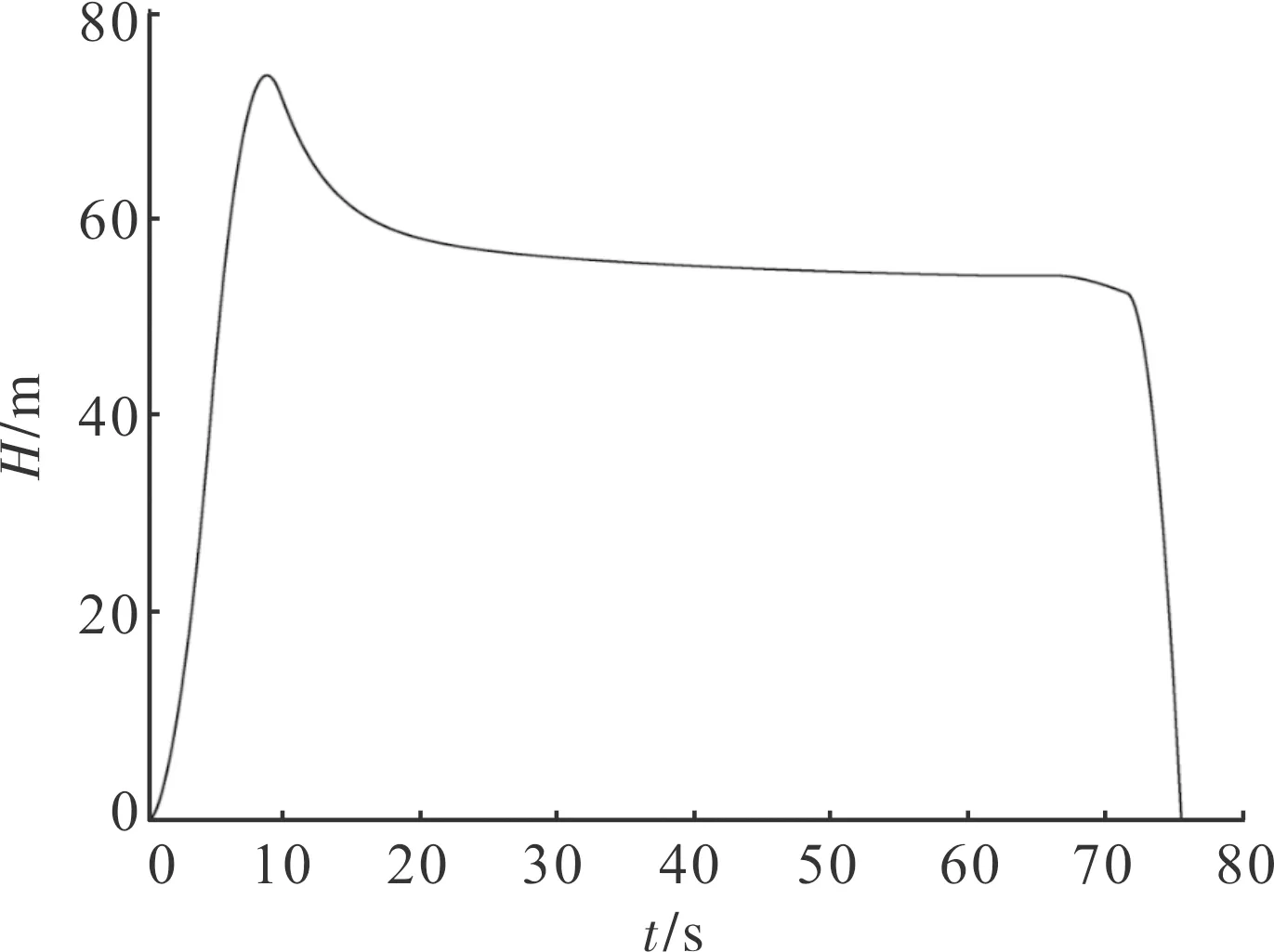
图9 飞行高度随时间的变化曲线

图6中，为悬浮火箭沿其飞行方向的速度，为沿飞行高度方向的速度，为垂直于和方向的速度。悬浮火箭在爬升段(0～5 s)，与迅速增加，在控制系统介入后，出现了小程度的震荡，接着稳定在25 m/s，则是迅速降低，回归为0，表示悬浮火箭保持定高低速飞行。

图7中，俯仰角初始值75°，通过姿态回路控制，俯仰角按照表1中变化，平飞段保持在83°，即悬浮火箭在平飞段保持大仰角飞行。

图8中，攻角在爬升段迅速增加，到平飞段时，保持在84°左右;图9中，悬浮火箭发射出筒后，高度在5 s时到达60 m，加入控制后，在15 s左右高度保持稳定，平飞段时间约为50 s。

不同飞行高度及飞行速度仿真结果如图10、图11所示。

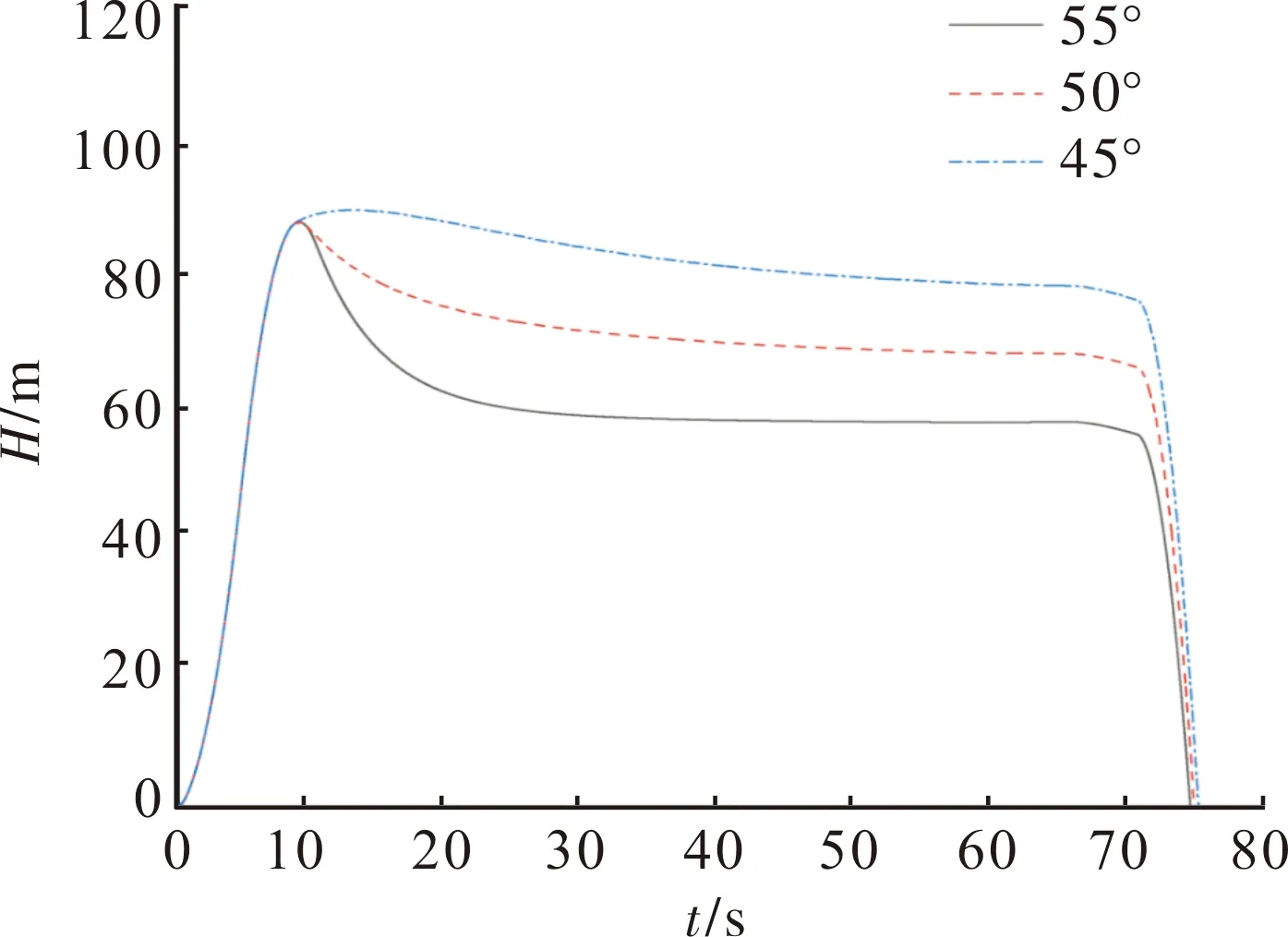
图10 3个俯仰角下不同悬浮高度随时间的变化曲线

图11 3个俯仰角下不同悬浮速度随时间的变化曲线

图10中，在=25 m/s的条件下，通过高度控制回路，悬浮火箭在60 m，70 m，80 m能够进行定高稳定飞行。图11中，在悬浮高度为60 m的条件下，通过速度控制回路，悬浮火箭在平飞段能够以20 m/s，25 m/s，30 m/s三个不同的速度进行稳定飞行。

通过上述的控制方案，图10和图11的仿真结果可知，一型悬浮火箭可以满足不同的悬浮高度及速度的需求。

5 结论

研究了一种基于推力矢量型固体火箭发动机的控制方案，通过仿真验证，控制方案是可行的，悬浮火箭爬升后，通过控制系统的介入，火箭的姿态、高度和速度能够迅速收敛，使得悬浮火箭能够满足作战时的飞行需求。

通过对不同悬浮高度和速度的弹道仿真，一型火箭能够满足不同的航迹需求。后续可以通过调整其控制参数，对其进行优化，使得悬浮火箭飞行状态快速收敛，使其在不同的作战需求下，火箭均能快速就位。

悬浮火箭的特点是能够自主飞行，抗风能力强，而海面上的气象条件恶劣，作战环境复杂，后续将针对于这些现实问题，通过仿真对悬浮火箭的性能进行研究分析。