基于群论的晶格扰动介质纳米孔阵列多重Fano 共振机理及演变*

陈颖 李美洁 赵蒙 王建坤

(燕山大学电气工程学院,测试计量技术与仪器河北省重点实验室,秦皇岛 066004)

基于全介质超构材料独特的电磁属性,提出了一种晶格扰动介质纳米孔阵列超构表面来激发近红外区域的多重Fano 共振.结合群论深入探究了该超构表面在其原胞为方形晶格构型与方形晶格对称性被破坏两情况下多重Fano 共振的形成机理及演变规律.研究表明,在方形晶格超构表面中,外部辐射连续体分别与由正入射平面波直接激发的双重简并模式共振干涉形成双重Fano 共振,且该共振与原胞中是否含孔及孔的形状无关,在晶格扰动超构表面中,原本不耦合的非简并模式由正入射平面波激发出来并与外部辐射连续体干涉形成Q 值更高的三重Fano 共振.进一步探讨了正入射平面波的xy 极化方向对上述五重Fano 共振的影响,结果表明,双重简并模式Fano 共振偏振无关,三重非简并模式Fano 共振偏振依赖.本文将为利用方形晶格构型的超构表面实现多重Fano 共振的激发及演变提供有效的理论参考.

1 引言

Fano 共振效应[1]源于原子系统中离散局域态与连续背景散射态之间的相消干涉,可在特定频段处产生陡峭的非对称光学响应谱线,导致入射电磁能量紧密束缚在光学结构周围,如0 维电介质球和棒[2,3]、一维无序结构[4]、波导中的二维腔[5]、三维光子结构[6]、晶格团簇[7]及超构材料等[8],从而实现极大地电磁局域增强.超构材料因具备普通光学材料难以取得的超常光学性能而在超光学领域具有极大的应用潜力,传统三维阵列超构材料的发展受制于集成难度大、工艺复杂等问题,而将超构材料的三维结构转为二维阵列平面结构则能突破其局限性,并将入射电磁能量限制在亚波长尺度内,因此由厚度远小于工作波长的原胞周期性排列而成的超构表面[9]得以研究和发展.

目前,国内外研究者们已经设计了大量形式新颖的Fano 共振超构表面,按组成材料可将其划分为等离子体型和全介质型,如Kong 等[10]提出了一种等离子体超构表面与光学微腔相结合的复合结构,由微腔激发的多个窄带共振峰与超构表面提供的连续背景散射态干涉形成多重Fano 共振.Zhang 等[11]提出了一种非对称的纳米圆环与交叉纳米棒多聚体全介质超构表面,交叉纳米棒集体振荡产生的电偶极米氏共振与纳米圆环提供的磁偶极米氏共振耦合形成单重Fano 共振.当光学研究波段推进到近红外及可见光范围时,金属材料的欧姆损耗及伴随其产生的热效应严重劣化了光学器件的效率,而全介质材料共振是由位移电流而不是传导电流驱动,在该波段下几乎对光透明,这使得Fano 共振超构表面研究聚焦于全介质材料.面对形式各异的全介质超结构群体,深入探究其中单重、双重乃至多重Fano 共振的激发机理及演变规律显得尤其重要.

分子光谱中构建的群论为超分子系统中Fano共振现象的产生提供了一种有效的解释.对于等离激元超分子来说,各个微纳颗粒间的表面等离激元(SPP)杂化共振对应由原子轨道建立分子轨道的过程,Brandl 等[12]从原子轨道建立分子轨道的机理出发,基于群论详细论述了如何由单个微纳颗粒的SPP 模式建立对称多微纳颗粒的SPP 模式,Hopkins 等[13]基于群论证明了等离子体对称低聚物中存在共同的Fano 共振激发机制,低聚物本征模的非正交使得本征模间可以相互干涉,从而导致Fano 共振的产生.Forestiere 等[14]利用群论证明在等离子体对称多聚体中,无需激发暗模式就可以实现Fano 共振.Gomez 等[15]结合分子点群的特征标表详细阐述了如何利用单个纳米柱体SPP 模式建立柱体阵列SPP 模式.全介质超分子系统由高折射率低损耗材料制成的介电粒子或介电粒子团簇组成,而基于群论结合近场分布详细阐述全介质超构表面因介电粒子团簇空间对称性改变引起的多重Fano 共振激发及演变等研究工作尚较少见.

本文提出了一种晶格扰动介质纳米孔阵列超构表面.基于群论结合反射光谱及近场分布对双重宽频带及三重窄带Fano 共振的形成机理进行详细分析,阐述了外部辐射连续体分别与方形晶格超构表面中由正入射波直接激发的双重简并模共振、经晶格对称性扰动激发的三重非简并模共振发生干涉而形成多重Fano 共振的物理机制及演变规律.应用Fano 模型定性分析各共振模式强弱,并利用数值模拟探究正入射波的xy极化方向对各共振模式的影响.

2 结构模型建立与理论分析

2.1 结构模型建立

图1 为本文提出的晶格扰动介质纳米孔阵列超构表面模型表征,其原胞为置于二氧化硅(SiO2)衬底上围绕中心O点对称地刻蚀4 个空心孔的方形截面硅(Si)纳米立方体.图1(a)和(b)分别表示实空间中方形晶格与晶格扰动原胞的俯视图,其中晶格常数为P=800 nm,硅体的方形截面边长c=680 nm ,方孔的边长a=110 nm,两相邻方孔的中心间距b=290 nm,上层硅体和方孔的厚度h=130 nm.晶格扰动是指通过引入晶格扰动参数r打破方形晶格原胞沿y轴的对称性,导致y轴负向两方孔的横截面积较y轴正向减少 ΔS=2×1/4πr2,r具体表示为与硅体等厚的四分之一硅(Si)圆柱体的底面半径,虚线框表征方孔减少的横截面积,当原胞为方形晶格时r=0 nm,对应硅体的横截面积为S=c2−4a2.当r设置为80 nm 时的超构表面示意图如图1(c)所示.应用Lumerical FDTD 仿真软件分析该超构表面的反射光谱与近场分布,数值模拟时,将该超构表面完全浸入折射率为1.33 的液体中,一束电场与磁场偏振分量相互正交且波矢量沿–z方向的平面波由该超构表面上表面入射,x和y方向均设置为周期性边界条件,z方向设置为完美匹配层(PML)边界条件,材料参数均采用Palik 折射率数据库数值[16].

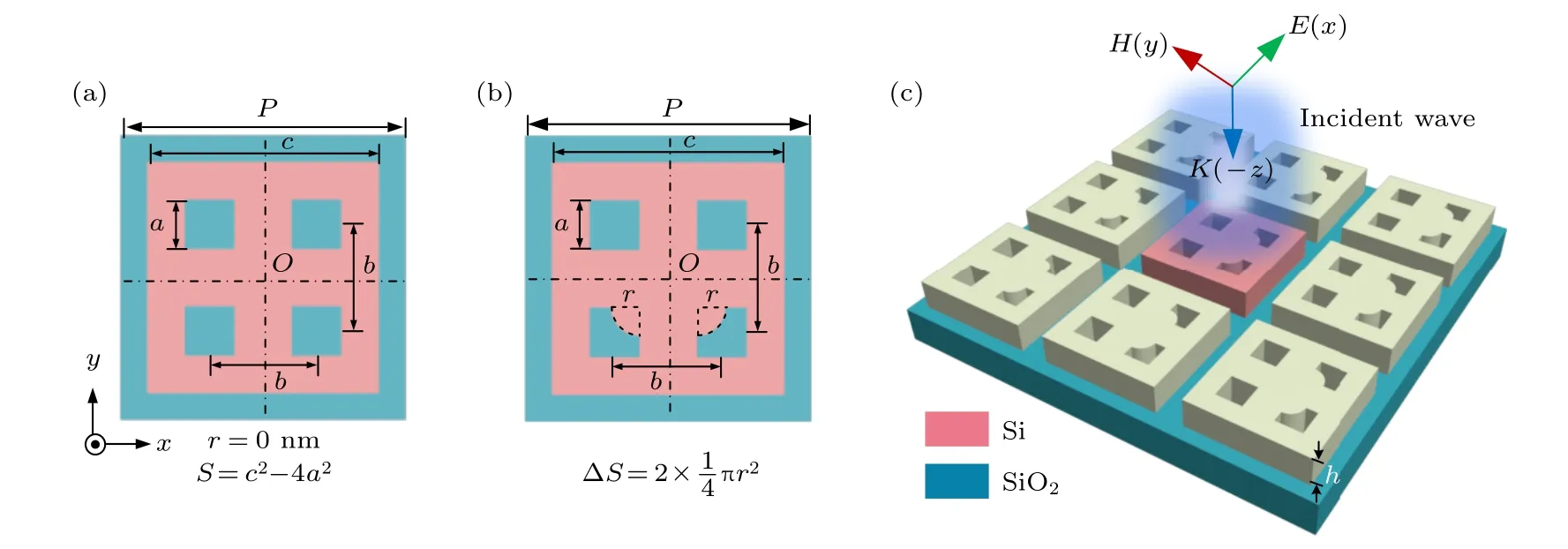
图1 晶格扰动介质纳米孔阵列超构表面模型表征 (a) 方形晶格原胞俯视图;(b) 晶格扰动原胞俯视图;(c) r =80 nm 时晶格扰动超构表面示意图Fig.1.Schematic diagram of dielectric nanohole arrays metasurface with lattice-perturbed:(a) Top view of unit cell with square lattice;(b) top view of unit cell with lattice-perturbed;(c) schematic diagram of metasurface with lattice-perturbed of r =80 nm.

2.2 理论分析

超构表面的整体电磁响应主要取决于原胞的性质,因此有必要首先揭示原胞的模态组成,该过程需结合原胞的空间面内对称性来展开,超构表面的全局对称性由原胞的点对称性来定义,故本文基于群论[17]研究该超构表面的电磁特性.当r=0 nm时,该超构表面的原胞由二维方形晶格排列的纳米方孔组成,方形晶格原胞的二维对称示意图如图2(a)所示,它同时具有旋转对称与镜面对称,因此该方形晶格超构表面的对称性可由C4v点群[18]描述.由表1 可知,该群在第一布里渊区中高度对称的波矢点G(kx=0,ky=0)有4 个一维不可约表示A1,A2,B1与B2和1 个二维可约表示E,这里的一维和二维分别指本征模是非简并与双重简并的,每种不可约表示都有其自身的空间对称性,当平面波正入射时,该方形晶格超构表面存在6 个本征模式,包括2 个简并模式与4 个非简并模式,其中2 个简并模式互为90°旋转重合版本,形成双重简并对,如图2(d)所示.用矢量E沿着x轴(ex)或者沿着y轴(ey)来区分正入射平面波的极化方向.

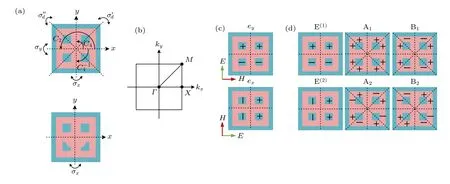
图2 原胞与模场对称性 (a) 方形晶格(上)与晶格扰动(下)原胞的二维对称示意图;(b) 方形晶格超构表面的第一布里渊区;(c) y 极化平面波(ey)与x 极化平面波(ex)的模场对称性;(d) 方形晶格超构表面中6 种本征模的对称性(同号区域对称,异号区域反对称)Fig.2.Symmetry of unit cell and mode field:(a) Two-dimensional symmetry operation for unit cell with square lattice(above) and lattice-perturbed (below);(b) the first Brillouin zone of square lattice metasurface;(c) symmetry of resonant mode field of ey and ex ;(d) symmetry of six eigenmodes in lattice metasurface (areas with the same sign are symmetrical and areas with different signs are antisymmetric).

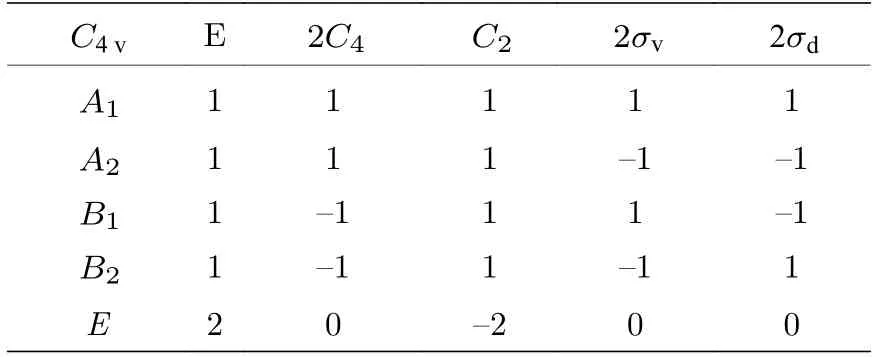
表1 C4v 点群的不可约表示的特征标表Table 1.Character table of irreducible representations of C4v point group.

只有当本征模式的对称性与正入射平面波的对称性相匹配时,共振模式才能够被激发.简并模式存在与正入射平面波对称性相匹配的成分因而能够发生耦合而被直接激发[19],包括E(1)模式与ey的Ey偏振分量及ex的Hy偏振分量,E(2)模式与ex的Ex偏振分量及ey的Hx偏振分量.但4 种非简并模式却不存在与正入射平面波对称性相匹配的成分,总体耦合强度为零,导致无法被激发而成为零共振线宽的非耦合暗模态.具体而言,非简并模式与ex,ey的耦合作用表达如下[20]:

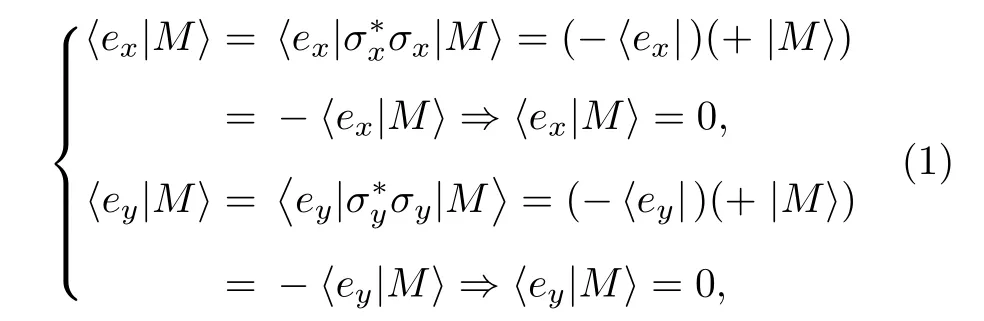
式中:M代表A1,A2,B1与分别对应σx与σy的逆变换.

由(1)式可知,正是非简并模式的镜像对称性阻止模式本身与外部辐射的耦合,故扰动模式的镜面对称性,则能够扰动模式与外部辐射的耦合,使两者间的对称性失配得到补偿.在方形晶格原胞中引入r=80 nm 的扰动后,晶格扰动原胞的对称性中仅σx得以保留,非简并模式沿x轴的对称性也随之未受到扰动,然而σy的打破导致非简并模式沿y轴的对称性受到破坏,非对称的非简并模式可被分成对称(s)模与反对称(as)模两部分[21],这两部分都具有σy对称性,对于A1与B1模式,对称模对应非简并模对称性,反对称模对应简并模对称性,对于A2与B2模式,对称模对应简并模对称性,反对称模对应非简并模对称性,故原始的非对称非简并模可被视作非简并模与简并模的加和,其中的简并模分量能够与正入射平面波耦合并辐射输出[22],导致A1,A2,B1与B2模式被激发而表现为可见线宽的亚辐射共振态.

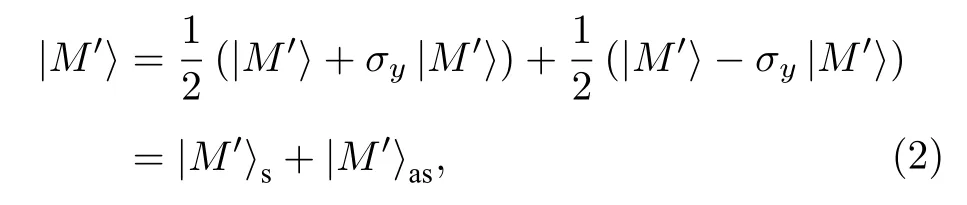
式中,M′代表非对称的A1,A2,B1与B2.

3 Fano 共振形成及演变

3.1 方形晶格超构表面

首先研究方形晶格超构表面的Fano 共振响应特性.如图3(a)中带三角的蓝色曲线所示,反射谱线 在λ1=1203.85 nm 与λ2=1499.06 nm 处出现2 个宽频带Fano 共振,将其简记为FR1 与FR2.方形晶格超构表面的6 种本征模式处于辐射连续域内,而其中4 种非简并模式为辐射连续域内的束缚态,因此,入射到方形晶格超构表面的电磁能量只能耦合到2 种简并模式并将其激发,同时与垂直的自由空间辐射连续体相互干涉形成Fano 共振[23].为更深入地了解FR1 与FR2 的物理性质,分析了其共振波长处的归一化电磁场分布并进行了硅体内部电流分布的笛卡尔多极矩展开.由图3(d)中FR1 处的归一化电磁场及其矢量分布可知,方孔间隙的位移电流在xoz截面内被激励成环形分布,导致其法向上的磁场得到增强,激发xoy截面内沿y方向的磁偶极共振MD1,如图3(f)MD1 的概念描述图所示,带箭头的蓝线圆圈表征位移电流,红线箭头表征激发的磁偶极矩.MD1 在xoy截面内的磁场分布沿x轴对称,沿y轴反对称,故其共振模式属于E(1),该模式由ex的Hy分量直接激发后与外部辐射连续体干涉形成FR1.由图3(d)中的归一化电磁场及其矢量分布可知,在xoy截面内,感应场位移电流在方孔间隙沿x方向逐渐增强,导致其切面yoz截面内形成强大的环形磁场,激发xoy截面内沿x方向的电偶极共振ED,如图3(g)ED 的概念描述图所示,绿线箭表征激发的电偶极矩.ED 在xoy截面内的电场分布沿x轴反对称,沿y轴对称,故其共振模式属于E(2),该模式由ex的Ex分量直接激发后与外部辐射连续体干涉形成FR2.图3(b)与图3(c)笛卡尔多极矩展开结果表明,磁偶极矩和电偶极矩分别对FR1 与FR2共振模式的远场辐射贡献最大.

图3 方形晶格超构表面在 ex 正入射条件下的数值模拟结果 (a) 完整硅板、扇形孔与方孔超构表面的反射光谱对比图;(b),(c) FR1 与FR2 处的笛卡尔多极分解;(d) FR1(FR2)在xoy 截面的归一化磁场(电场)分布 |H|(|E|)及xoz(yoz)截面的归一化电场(磁场)分布 |E|(|H|);(e) 完整硅板与扇形孔超构表面在xoy 截面的归一化电磁场分布(以下场图中的白线框均表征结构轮廓);(f),(g) MD1 与ED 的概念描述图Fig.3.Numerical simulation of square lattice metasurface under ex :(a) Reflectance spectrum comparison of metasurfaces with complete silicon block,scalloped holes and square holes;(b),(c) cartesian multipole decomposition of FR3,FR4 and FR5;(d) normalized magnetic(electric) field distributionin |H| (|E|) in xoy section and normalized electric(magnetic) field distribution |E| (|H|)in xoz (yoz) sectionof FR1(FR2);(e) normalized electromagnetic field distribution in xoy section of metasurface with complete silicon block,scalloped holes(white boxes in the following field diagrams is structural outline drawing);(f),(g) conceptual description of MD1 and ED.

为进一步分析双重简并模式Fano 共振的激发特性,将单元胞同为方形晶格的完整硅板结构、90°扇形孔结构(孔半径与方孔边长相等)在ex正入射条件下的Fano 共振响应特性与该方孔结构进行对比.如图3(a)三结构的反射光谱对比图所示,完整硅板结构由于空间体积增大引起上层硅体等效折射率增加而产生2 个共振波长红移的Fano 共振,90°扇形孔结构则因空间体积与该方孔结构相差不大而出现2 个共振波长几乎与FR1、FR2 相同的Fano 共振.通过观察图3(e)完整硅板与90°扇形孔结构共振处的近场分布可知,两结构的局域电磁场及其矢量分布与该方孔结构大体保持一致,故两结构中的共振模式与该方孔结构相同.上述研究结果表明,方形晶格超构表面仅支持双重简并模式Fano 共振,且该共振与超构表面原胞中是否含孔及孔的形状无关.

3.2 晶格扰动超构表面

当该超构表面的r=80 nm 时,方形晶格的面内对称性被破坏,4 种非简并模式与外辐射波的耦合强度不再为零,入射电磁能量耦合到4 种非简并模式后与外部辐射连续体相互干涉形成Fano 共振[24].如图4(a)中带圆圈的红色曲线所示时,该结构在ex正入射条件下产生了除之前讨论的FR1与FR2 以外的3 个带宽极窄的Fano 共振,其共振波长分别对应λ3=1074.8 nm,λ4=1093.35 nm,λ5=1577.74 nm,依次简记为FR3,FR4 与FR5.同时r的增加引起空间体积增大进而导致上层硅体的等效折射率增加,FR1 与FR2 对应的共振波长发生红移,现分别为λ1=1207.13 nm 与λ2=1504.39 nm,但共振模式未发生改变.应用Fano模型定性地分析FR1-FR5 的模式特性及共振强弱,其表达式如下[25]:

图4 晶格扰动超构表面的反射光谱图与拟合曲线模型 (a) ex 与 ey 正入射条件下的反射光谱对比图;(b) ex 正入射条件下FR1-FR5 的拟合曲线Fig.4.Reflection spectra and fitting curve model of lattice perturbed metasurface:(a) Comparison of reflectance spectrum under ex and ey ;(b) fitting curve of FR1-FR5 under ex.

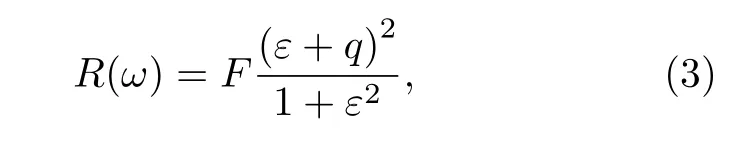
式中:ε=2(ω−ω0)/Γ,ω0和F分别代表Fano 共振频率与线宽;F为连续态与离散态的耦合系数;q为Breit-Wigner 参数,表征Fano 共振轮廓的非对称性.选取FR1-FR5 的光谱特征利用该模型进行拟合,表2 展示了该模型中表征Fano 共振特性的主要参数值,可以看出解析推导与数值模拟呈现较好地吻合,拟合曲线如图4(b)所示.通过表2 参数比值ω0/Γ求 取FR1-FR5 的共振Q值,显然FR3、FR4与FR5 远大于FR1 与FR2,故经晶格扰动激发的Fano 共振强度更高.

表2 表征Fano 共振特性的主要参数值Table 2.Main parameters that characterize the resonant properties of Fano.

由于具有特定对称类型的非简并模式只能耦合到具有相同对称类型的正入射平面波中,因此这里通过共振模式在xoy截面的电场矢量分布的对称性来对非简并模式的激发进行解释[26].由图5(a)与图5(d)可知,FR3 处的局域电场聚集在硅体边缘与内部.硅体边缘的电场矢量分布属于A2模式,硅体内部的位移电流在xoy截面内呈现一逆一顺2 个反向闭环分布,导致yoz截面内的磁场在2 个闭环的中心部分得到增强,激发2 个沿+z、–z方向的磁偶极矩,其与ex的Hy分量构成yoz截面的流动环形磁场,诱导xoy截面内沿x方向的电环偶极共振TD1,如图5(g)TD1 的概念描述图所示,带箭头的蓝线圆圈表征位移电流,带箭头的红线圆圈表征激发的磁偶极矩M,蓝线箭头表示诱导的电环偶极矩T.TD1 模式与A2模式的杂化电场在xoy截面内整体沿x轴对称,沿y轴反对称,故该杂化共振仅能由正入射的ex激发,后与外部辐射连续体干涉形成电环偶响应FR3.由图5(b)与图5(e)可知,FR4 处的局域电场仍聚集在硅体边缘与内部,并显现向内部转移的趋势.硅体边缘的的电场矢量分布同样属于A2模式,而硅体内部上下两侧的反相圆形位移电流的流向与FR1 相反,从而激发垂直于硅体表面的反相圆形磁矩分布,诱导一个与硅体表面平行的反相强环向力矩TD2,如图5(h)TD2 的概念描述图所示.综合来看,FR2 处的杂化电场分布整体与FR1 反相,但对称性未发生改变,故该杂化共振仅能由正入射的ex激发,后与外部辐射连续体干涉形成电环偶响应FR4.由图5(c)与图5(f)可知,FR5 处的局域电场已经大部分集中在小孔内部,ex的Ex分量导致上下两对小孔在其左右两侧产生反相极化异号电荷,将该电荷形成的位移电流矢量沿x方向的分量相互抵消后发现诱导产生了2 个沿y方向反相平行的电偶极子,光场在此处散射并进入硅体内部呈现xoy截面的环形电场分布,激发沿z方向的磁偶极共振MD2,如图5(i)MD2 的概念描述图所示.其电场矢量分布属于B2模式,该模式主导的杂化电场整体关于x轴对称,故仅能由正入射的ex激发,后与外部辐射连续体干涉形成FR5.图5(j)—(l)笛卡尔多极矩展开结果表明,电环偶极矩对FR3 与FR4 共振模式的远场辐射贡献最大,磁偶极矩对FR5 共振模式的远场辐射贡献最大.

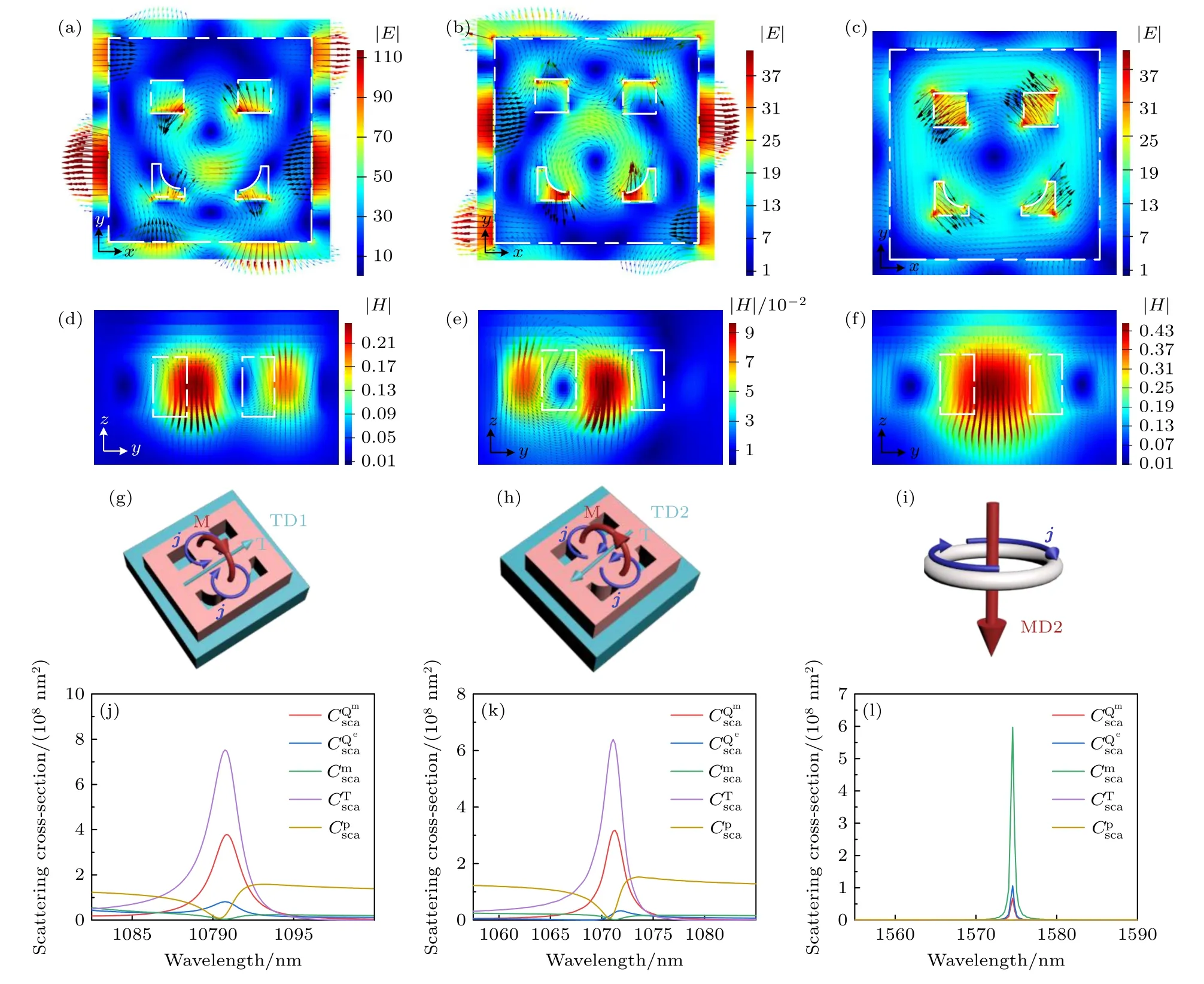
图5 晶格扰动超构表面在 ex 正入射条件下的近场分析与笛卡尔多极分解 (a)—(i) FR3,FR4 与FR5 在xoy 截面的归一化电场分布 |E| 、yoz 截面的归一化磁场分布 |H| 及TD1,TD2 与MD2 的概念描述图;(j)—(l) FR3,FR4 与FR5 处的笛卡尔多极分解Fig.5.Near-field analysis of lattice-perturbed metasurface under ex and cartesian multipole decomposition:(a)–(i) Normalized electric field distribution |E| in xoy section and normalized magnetic field distribution |H| in yoz sectionof FR3,FR4 and FR5,and conceptual description of TD1,TD2 and MD2;(j)–(l) cartesian multipole decomposition of FR3,FR4 and FR5.

为证明非简并模式Fano 共振只出现在ex正入射条件下,将晶格扰动超构表面在ey正入射条件下的反射光谱及近场分布与前文进行对比.如图3(a)中带方块的黑色曲线所示:FR3,FR4 与FR5 在反射光谱中完全消失,同时反射谱线中又出现2 个分别与FR1,FR2 基本重合的Fano 共振,记为共振1 与共振2.根据图6(a)两共振处的归一化电磁场及其矢量分布可知,两共振仍分别为磁偶极模式与电偶极模式,其与图3 中MD1 与ED 的区别在于xoy截面内磁偶极矩与电偶极矩的方向发生了90°旋转,故共振波长处的电场矢量分布的对称性也发生了改变,改变后其共振模式分别对应E(2)与E(1)模式,而双重简并模式本身互为90°旋转重合版本,因此同一Fano 共振处的共振模式在本质上未发生改变,图6(b)笛卡尔多极矩展开结果表明,磁偶极矩与电偶极矩分别对共振模式1 与共振模式2 的远场辐射贡献最大.综上所述,双重简并模式共振可以同时出现ex与ey正入射条件下,且两情况下各共振处对应的共振模式相同,而非简并模式共振只出现在对称类型与之相同的单一极化条件下,这验证了文献[27]中指出的非简并模式的非简并性质将导致当结构的对称性被破坏时,这些模式只能耦合到正入射波的单个极化方向,同时也证明了ex正入射下非简并模式Fano 共振的激发主要是因为晶格对称性破缺.

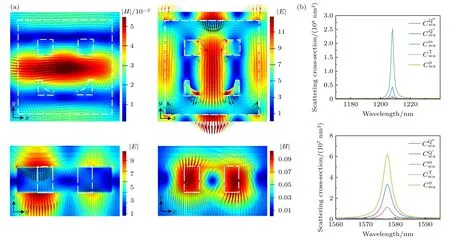
图6 晶格扰动超构表面在 ey 正入射条件下的近场分布 (a) 共振1(共振2)在xoy 截面的归一化磁场(电场)分布 |H|(|E|)及yoz(xoz)截面的归一化电场(磁场)分布 |E|(|H|);(b) 共振1 与共振2 处的笛卡尔多极分解Fig.6.Near-field distribution of lattice-perturbed metasurface under ey :(a) Normalized magnetic(electric) field distributionin |H|(|E|) in xoy section and normalized electric(magnetic) field distribution |E| (|H|) in yoz(xoz) sectionof resonance 1(resonance 2);(b) cartesian multipole decomposition of resonance 1 and resonance 2.

4 结论

基于全介质材料的电磁特性,提出了一种晶格扰动介质纳米孔阵列超构表面.通过打破方形晶格原胞的镜面对称性,非简并模式发生退化,退化后的简并模式分量与外辐射波的耦合导致原本不耦合的非简并模式被激发出来,使得该结构在所选近红外波段内实现了五重Fano 共振,包括双重简并模式共振与外部辐射连续体干涉形成的磁偶响应FR1 与电偶响应FR2,非简并模式主导的杂化共振与外部辐射连续体干涉形成的电环偶响应FR3,FR4 及磁偶响应FR5.应用Fano 模型定性分析了五重Fano 共振的强弱,结果表明,非简并模式Fano共振的Q值远高于简并模式Fano 共振.另外探究了正入射平面波的xy极化方向对五重Fano 共振的影响,发现简并模式Fano 共振偏振无关,非简并模式Fano 共振偏振依赖.本文的研究结果将对利用方形晶格超构表面操控多重Fano 共振的激发及演变具有一定的理论指导意义.