中职数学中数形结合思想的应用

刘永强

【摘要】数形结合思想是解决数学问题的重要数学思想之一，它“以形助数”，化抽象为直观，“以数解形”，将“形”的特征用“数”的严密性和准确性表示出来。抽象思维与形象思维的结合，实现了优化解题途径的目的，有效帮助学生理解抽象的数学问题，有助于学生对数学知识获得过程及理论来源的理解。本文以实际例子论述数形结合思想在中职数学教学中的应用，并给出了数形结合方法的教学建议。

【关键词】中职数学；数形结合思想；应用；建议

【中图分类号】G718.3【文献标志码】A【文章编号】1004—0463（2022）10—0061—04

新《中等职业学校数学课程标准》课程任务指出：“使中等职业学校学生获得进一步学习和职业发展所必须的数学知识、数学技能、数学方法、数学思想和活动经验。”数形结合思想是其中重要的数学思想之一，能有效帮助学生理解抽象的数学问题，优化解题途径。“数”和“形”是数学中两个最古老、最基本的研究对象，主要研究数字、算术、数量关系等与图形知识之间的关系，它们相辅相成，紧密结合，在一定条件下又可以相互转化。我国著名数学家华罗庚曾说过：“数形结合百般好，割裂分家万事休。”诸多数学研究者和数学教师对这一课题的研究颇多，但其侧重点不同。丁杭缨认为：“数形结合既是教师教学的重要目标，也是学生数学学习的目的。”[1]李雪认为：“数形结合的实质是把抽象的代数与形象的图形结合起来，代数问题与图形问题彼此转化。”[2]顾越岭认为：“考虑问题时数、形兼顾，将其直观性与抽象性有机结合起来，使我们的认识更加全面、更加深刻。”[3]笔者搜索知网，查阅大量关于数形结合思想的研究资料，发现研究者们的观点基本一致，认为数形结合就是把代数问题与几何图形结合起来，“以形助数，以数解形”，化抽象为具体，达到事半功倍的效果[4]。

绝大多数中等职业学校的学生是中考后分数未能过普高录取线的考生，他们文化课底子差、基础弱，尤其在数学学习上困难重重。很多学生在小学阶段就落下了数学基础知识，基本数学概念不清；常用公式、運算法则及性质理解不透，相互混淆；基本运算能力差，有学生甚至连计算2-（-8）这样简单的运算都要考虑很长时间，学习上心有余而力不足，严重影响了学生学习的积极性。为此，教师改变传统的数学教学思想和方法，注重数学学科内在的、学科素养——“以形助数，以数解形”，化抽象为直观，优化解题路径，激发学生的学习兴趣。

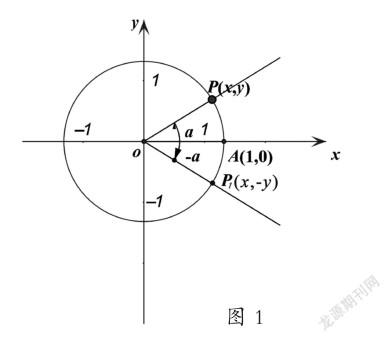
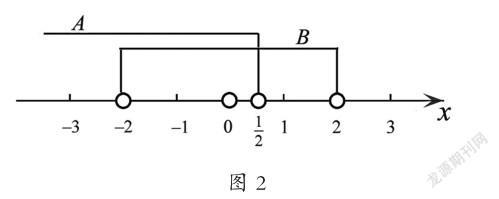
可见，处理集合问题，用数形结合的方法，可以使集合之间的关系及运算直观化，更容易求解问题的结果。

在数学教学中，很多教师受“高考模式”影响，沿用传统的教学思想，重结果轻过程，学生获得的数学知识比较死，增加了记忆量，还容易混淆。运用数形结合思想，使学生对数学结论获得本源性的过程体会，从实质上理解了知识的来龙去脉，化抽象为具体，直观呈现，降低了学生的理解难度。

3.以数解形，将“形”的特征用“数”的严密性和准确性表示出来。“形”虽然在直观性上有很多优势，能把抽象的问题形象地表示出来，但在定量上，无论是简单的还是复杂的图形，都必须借助于“数”，用“数”精准地描述“形”的特征、数量关系，两者之间的完美结合，使得数学知识学习不断向纵深方向发展。例如，函数y=f（x）的图象如图4所示，观察图形，让学生把从图上看到的所有图形特征说出来。这就需要用数学语言完整地描述图形特征，汇总如下：

（1）函数y=f（x）的定义域[-3，3]，值域[-1，2]；

（2）当x=-1时，函数有最大值2，当x=2时，函数有最小值-1；

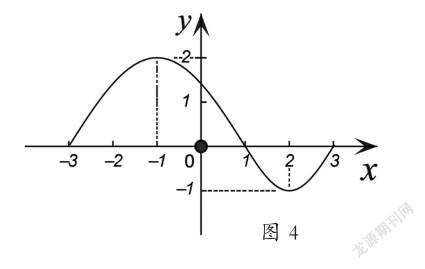
（3）在整個定义域上，函数不具有单调性，但在定义域的某些区间上具有单调性，如在区间[-3，-1]∪[2，3]上函数单调递增，在区间[-1，2]上单调递减；

（4）这是一个非奇非偶函数。

用“数”把“形”所表现出的所有特征、性质进行总结，训练了学生观察、分析、总结问题的逻辑能力，加深了对函数性质等相关知识的理解。

中职数学教材在编写上以学生的年龄特点、心理特征及学习基础为出发点，突出职业性和基础性，依照“实例”“观察”“新知识”“知识巩固”“练习”“现代信息技术应用”“阅读与欣赏”等板块组织教学。对学生而言，数学知识的呈现很明确，而数学知识中蕴含的数学思想却是看不见、摸不到的，这就需要教师在课堂教学中潜移默化地渗透。中职数学教学思想包含很多种，知识化归、数形结合等数学思想方法之间既密切联系又各具特色。在运用数形结合思想探究或解决问题时，需要把握以下几点。

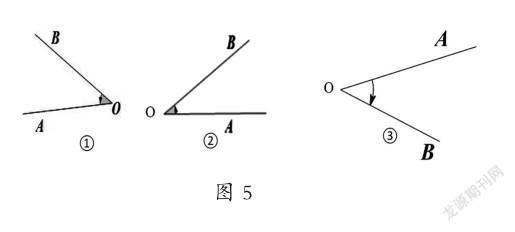
1.概念教学中渗透数形结合思想。数学概念犹如法律条文，其基础性地位特别高，是数学重要知识点的浓缩。学生对概念的认知过程要经过分析、比较、抽象、提炼、概括和归纳等思维加工，而不是简单的记忆和理解。实际教学过程中，教师要尽量把抽象的理性知识通过“形”直观表示，加深学生对概念的理解，从而提升学习效果。如小学的分数概念，初中数学中的绝对值、相反数等概念性知识的讲解都可以运用数形结合思想完美阐释。中职数学基础模块上册第五章学习任意角的概念时，需要大量渗透数形结合思想，使抽象的概念具体化。如理解正负角的概念，从图5的三个图形中直观观察出它们都是角，记作∠AOB，但意义不同：图①和图②是正角，图③是负角，教师在讲述概念时要结合图形紧扣角是由始边绕着顶点按照顺时针方向还是逆时针方向旋转形成的这一关键点，学生就会心领神会。

2.公式、定理教学中感悟数形结合思想。数学学习中，涉及到的公式和定理很多，也比较抽象，记忆起来比较困难，尤其数学公式容易混淆、记错。其主要原因在于学生对公式、定理的本源性理解不到位，这就需要教师在讲解知识时合理利用数形结合思想，帮助学生从“形”中领悟公式、定理的几何意义，加深理解，记忆公式、定理。如中职数学诱导公式、直线与圆的方程等数学知识，都可以通过图形帮助记忆理解。

3.解题方法中突出数形结合思想。只有在解题过程中突出数形结合思想方法，才是最好的运用。虽然数形结合思想方法贯穿于数学学习和研究的始终，但运用于解题方法教学中要注意把握度和适用性原则。中职学生数学底子薄弱，在教学过程中要关注问题中涉及的“数”与潜在的“形”之间是否具有等价性，能否使问题简单化。

总之，数形结合既是“数”与“形”的等价结合，也是数学思想与数学研究及学习方法的有机结合，在运用过程中要注重由“数”的抽象到“形”的直观转化以及由“形”到“数”的精准描述。

[1]丁杭缨.给学生一个立体的“数学”——例谈“数形结合”[J].人民教育，2010（07）：39-42.

[2]李雪.初中数学数形结合思想教学研究与案例分析[D].河北：河北师范大学，2014：63.

[3]顾越岭.数学解题通论[M].桂林：广西教育出版社，2000：120.

[4]游雪峰.数形结合在中职数学教学中的应用研究[A].教学应用就业，2016.

[5]徐文龙.“数形结合”的认知心理研究[D].桂林：广西师范大学，2005：06-08.

（本文系2020年度甘肃省“十三五”教育科学规划一般课题“‘三教’改革背景下中职文化课教学困境及对策研究”的研究成果，课题立项号：GS[2020]GHB3125）

编辑：徐春霞