计及新能源大规模接入电网的需求侧精细化建模研究

房 俏，李 山，刘文学，蒋 哲，李常刚

（1.国网山东省电力公司电力科学研究院，山东 济南 250003；2.山东大学电气工程学院，山东 济南 250061）

0 引言

随着社会经济发展，电力需求也大幅增长。近年来，电力负荷不断增长，电力系统暂态电压失稳事故也时有发生［1-4］，诸如美国加州东北部电网大面积停电事故、美国西部1996 年7 月2 日大停电、伦敦南部地区大停电等。电力系统失稳导致的停电往往带来巨大的经济损失和社会影响，因此，研究电力系统稳定性具有重要意义［5］。

电力系统稳定性是指在给定的初始运行方式下，系统受到物理扰动后仍能够重新获得运行平衡点，且在该平衡点大部分系统状态量都未越限，从而保证系统完整性的能力［6］。电力系统两大国际组织国际大电网会议（Conseil International des Grands Réseaux Electriques，CIGRE）和国际电气与电子工程师学会电力工程分会（Institute of Electrical and Electronic Engineers，Power Engineering Society，IEEE PES）综合考虑电力系统失稳的物理特性、扰动程度以及时间尺度等方面，将电力系统分为功角稳定、电压稳定和频率稳定三类［7］。在系统发生大扰动导致失稳后，通常表现为电压失稳和功角失稳两种形态［8］，功角稳定主要指大电网中的同步发电机遭受扰动后，保持相互间同步运行的能力；电压稳定则是指系统在初始运行点处，经历扰动后，维持可接受的稳态电压能力。

电力系统的暂态稳定分析可以归结为微分-代数方程组的求解问题。由于电力系统的复杂性，对电力系统的稳定性分析十分困难，常见有两种方法，暂态能量函数法和数值仿真法［9］。

暂态能量函数法也称为直接法，由李雅普诺夫的运动稳定性理论发展而来。直接法通过构造能量函数，并根据系统扰动方程式计算得出该函数的时变性，以此确定非线性系统的稳定性质［10］。但是，由于大电网的李雅普诺夫函数建立困难，难以确定相关不稳定平衡点（第一类平衡点），因此无法用于分析实际大系统。

数值仿真法的基本思想是求解电力系统的微分-代数方程组，通常采用潮流的解作为初值，用数值积分方法求出描述扰动后微分方程组的时间解［11］。数值仿真法可以适应不同详细程度的元件数学模型，分析结果准确可靠。数值仿真法虽然无法给出系统运行点在各个方向上的裕度，但是由于其分析大电网的优越性以及在技术应用方面相对成熟，在系统暂态稳定分析中广泛应用。目前，国家电力调度通信中心的大电网仿真分析多基于中国电力科学研究院研发数值仿真程序“电力系统分析综合程序”（Power System Analysis Software Package，PSASP）［12］，交流同步电网数据的元件库均录入中国电力科学研究院提供的国家电网仿真计算数据平台［13］。

元件模型的精细化程度决定了数值仿真的准确性，通常大电网暂态仿真使用发电机六阶模型、直流准稳态模型、线路集中参数模型等能够较为准确描述电网的动态特性，满足仿真要求［14-16］。但是，由于仿真资源有限，因此大电网建模对于需求侧的处理较为简略，多采用等值的综合负荷，即负荷加感应电动机模型代替配电网［17-18］。同时，电力系统呈电力电子化趋势。在输电系统中，柔性交流和柔性直流输电技术逐步应用，特高压直流输电快速发展。并且，随着新能源大规模接入电网，异步电源均需要电力电子接口装置，使输出的交流电与电力系统保持同步。传统用单机倍乘机组等值新能源场站，并用一套典型参数作为新能源控制参数的建模方法也无法精确描述新能源的动态特性，从而降低了数值仿真的正确性与可靠性。

针对电网模型简化对电力系统数值仿真带来的影响，提出了一种区别传统等值模型的大电网精细化建模方法，对网络结构拓扑展开建模，考虑主网架与辐射状配网，并将新能源场站建模至机端。承接前期新能源建模与控制参数实测工作，在新能源建模中为不同新能源场站配套新能源实测控制参数［19］，有利于新能源在仿真分析中的动态特性更加贴合实际。以某交直流混联同步电网数据作为实例，某受端电网采用传统等值模型与集中式新能源全电压等级模型两种方式进行建模，并对不同模型下暂态电压稳定性及主要影响因素进行对比分析。

1 基于等值模型的大电网仿真建模

电力系统由各种不同元件组成，在仿真计算中，通过仿真软件计算大电网的潮流，小干扰稳定，或者分析大电网的暂态特性等，首先要研究各元件的特性，建立其动态模型。在此基础上，根据系统的具体结构，即元件的相互关系，建立全系统的数学模型，并通过适当的数学方法进行求解。

目前，PSASP 元件库中包括常见电力系统元件如：发电机、变压器、负荷、交流线、直流、新能源等系统常见元件模型及其控制器，基本满足仿真计算及分析需求。但是，考虑到节省计算资源以及缩短计算时间，实际工作中，用于大电网稳定分析的数据建模止于220 kV 变电站，220 kV 以下电压等级的变电站及其末端所接入的负荷与新能源场站，均以等值负荷与等值新能源机组直接接入220 kV变电站的高压侧及中压侧母线。

某220 kV 变电站负荷及新能源等值模型如图1所示。220 kV 变电站下接变电站及线路全部被省略，所供负荷总和以等值负荷代替，接入220 kV 变电站中压测。等值负荷考虑静态负荷和感应电动机两部分，这种负荷模型能够计及感应电动机转子绕组中的暂态过程，但是忽略了感应电动机定子回路的暂态过程。新能源模型省略升压变及箱变，仅用功率单机倍乘机组等值后接入变电站高压侧或中压侧，风机仅采用双馈风机模型（Doubly Fed Induction Generator，DFIG）。双馈风机与光伏电源分别套用参数为中国电科院提供的一套典型参数，此套参数在故障后低穿期间动态响应能力较差，较为保守。

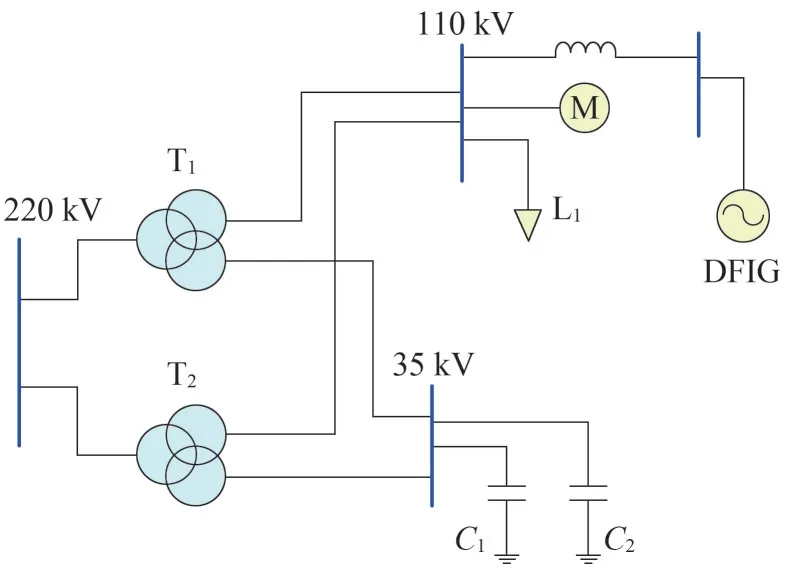
图1 基于等值模型的变电站建模

2 基于拓扑模型的大电网仿真建模

随着数值积分算法的不断优化以及计算资源的逐渐充裕，大电网仿真计算对元件精细化建模的要求逐渐提高。借助中国电力科学研究院提供的数据平台，可将110 kV及以下电压等级变电站，直至10 kV 用户站的元件稳态参数及暂态参数、网络拓扑结构录入其中，达到电网精细化建模的目的。

同时，新能源大规模接入电网不仅带来了随机性和不确定性，也改变了大电网的动态特性。使用新能源典型参数的暂态仿真显然无法为离线分析提供更加可靠的电网特性分析依据。因此，依据新能源实测参数建模，不同场站不同动态特性的新能源变流器控制参数也同时被录入至国家电网仿真数据平台中，形成了更为精细化的拓扑模型加新能源实测参数的仿真模型。图1 所示变电站及所接入的低电压等级拓扑模型如图2所示。

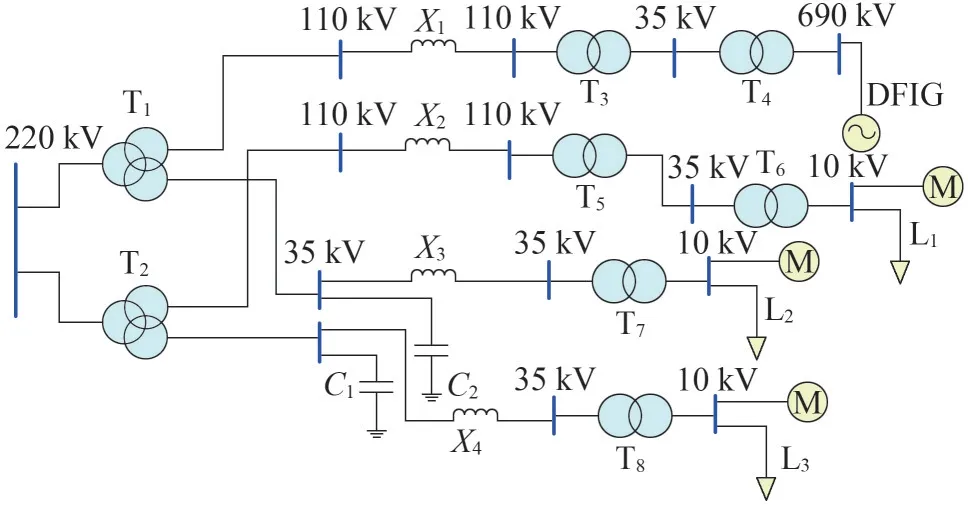
图2 基于拓扑模型的变电站及接入厂站建模

此种建模更为精细化，不再忽略220 kV 以下电压等级网络拓扑结构及线路参数，负荷接入实际低电压等级用户站。新能源场站建模中，考虑升压变及箱变，将新能源模型建至机端，且配合此新能源场站逆变器机组相应型号实测参数。

3 仿真算例

3.1 算例参数

采用某交流同步电网数据进行分析。如图3 所示，某受端电网通过十回交流线路由同步电网1 受电、通过三回直流线路分别由同步电网2、同步电网3受电。

采用传统的等值模型+新能源典型参数、拓扑模型+新能源典型参数以及拓扑模型+新能源实测参数3 种模型，电网交直流受电断面如图3 所示。基于PSASP7.61软件版本，对系统进行仿真分析。

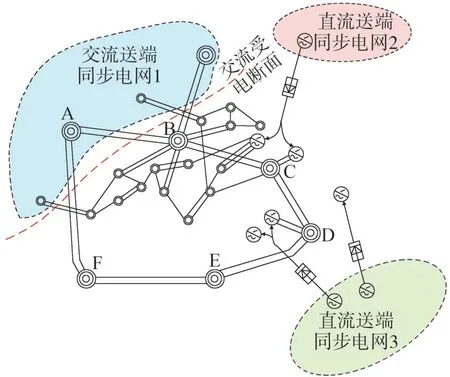
图3 某受端电网交直流受电断面

3.2 电压稳定性

1 000 kV 变电站A 站至B 站双回线路发生三永N-2故障，故障导致受端电压崩溃，临界运行方式下，受端电网采用3种模型的交直流受电能力如表1所示。

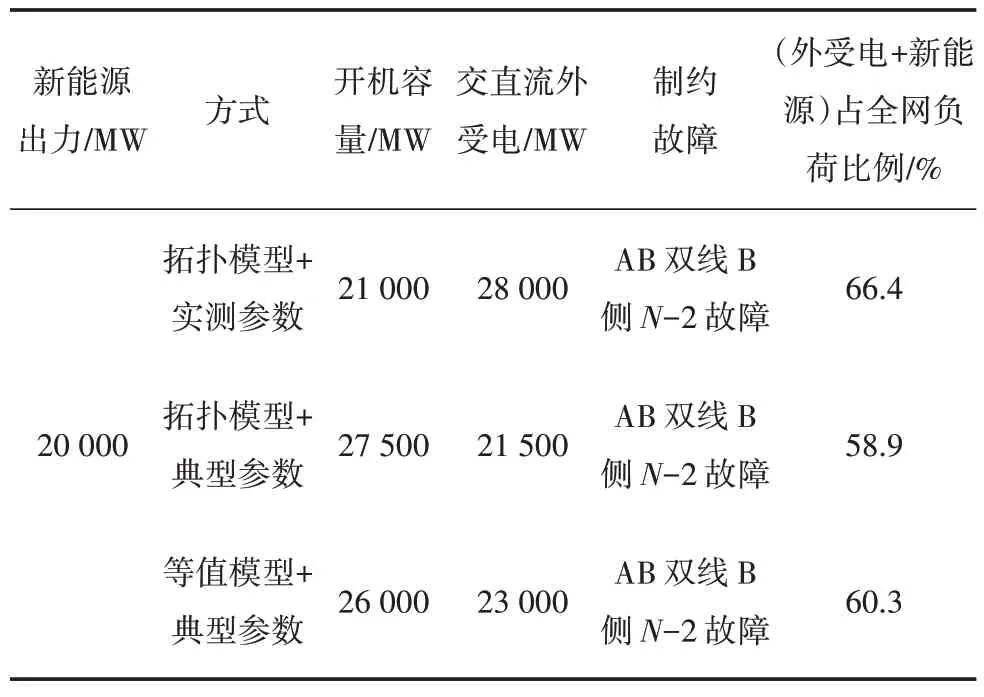
表1 不同建模方式受电能力对比

分析表1 数据，对比3 种建模方法。相同负荷水平及新能源出力情况下，拓扑模型+新能源实测参数建模的外受电+新能源占全网负荷的比例最高，表明此种建模方法下受电能力最高，电压稳定性最好。拓扑模型+新能源典型参数建模此项比例最低，表明此种建模方法下受电能力最低，电压稳定性最差。

4 算例分析

不同建模方式下受电能力主要与两个影响因素相关，分别为新能源参数差异以及网架结构差异。

4.1 新能源控制参数差异

对比拓扑模型+新能源实测参数及拓扑模型+新能源典型参数两种建模方式，新能源低压穿越期间控制参数，影响新能源机组动态特性，进而影响故障后电网的有功缺额。

新能源低压穿越期间采用指定电流控制，低压穿越期间双馈风机指定电流控制如式（1）所示，双馈风机参数如表2所示。

表2 某双馈风机有功控制参数对比

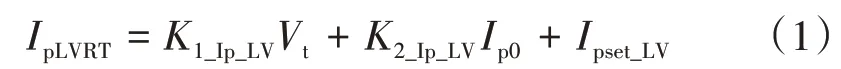
式中：IpLVRT为机组低压穿越运行时的有功电流分量；K1_Ip_LV和K2_Ip_LV为有功电流计算系数；Vt为端电压幅值；Ip0为初始有功电流；Ipset_LV为有功电流整定值。

依据式（1）可知，有功降落主要与电流计算系数及初始有功电流、机端电压相关。新能源机组稳态相同，则电流初始值Ip0相同。拓扑模型+新能源实测参数及拓扑模型+新能源典型参数两种建模方式均采用拓扑网架结构，因此故障后机端电压跌落程度相近，如图4 所示。动态中新能源的有功出力与K1_Ip_LV与Vt的乘积相关性最大。以表2中某实测参数与典型参数为例。1 s 故障后，新能源进入低穿。低压穿越期间，某实测参数新能源机端功率如图5 中蓝色曲线所示，实测参数K1_Ip_LV较高，电流指令较高，最终计算得到的有功参考值高，因此机端有功降落少。典型参数K1_Ip_LV为零，有功电流指令与机端电压解耦，低压穿越期间有功下降明显，如图5中绿色曲线所示。

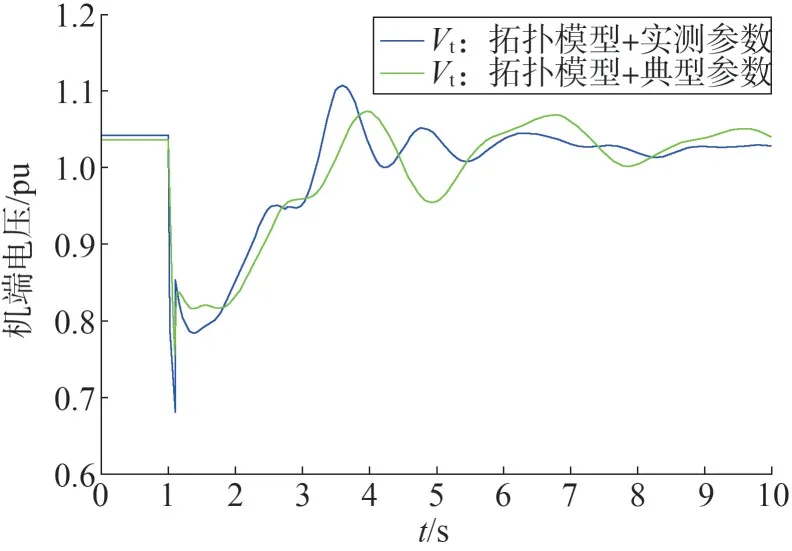
图4 不同新能源参数DFIG机端电压对比

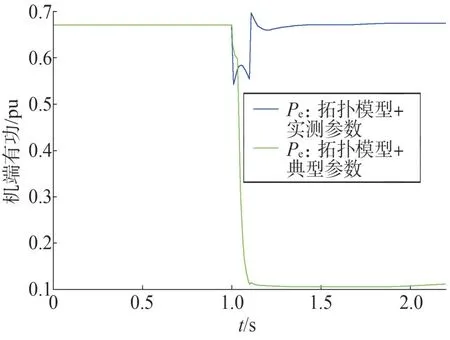
图5 不同新能源参数DFIG机端有功对比

4.2 网架结构差异

对比拓扑模型+新能源典型参数与等值模型+新能源典型参数两种建模方式，在新能源无功控制中，无功控制与机端电压跌落程度密切相关，而有功降落只与初始有功电流相关，因此两种方式有功降落差距不大，有功对电压稳定性影响差别相近，如图6所示。

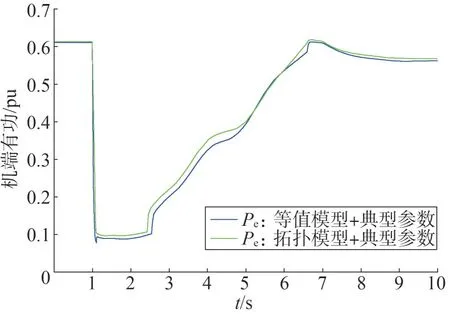
图6 不同拓扑建模DFIG机端有功对比

根据低穿期间无功控制式（2）及表3 所列参数可知，新能源机端无功支撑与无功电流计算系数正比于电压跌落差VLin-Vt。等值模型与拓扑模型电压跌落情况如图7 所示。拓扑模型新能源机端距离故障电气距离远，电压跌落浅，无功发出少，对主网架无功支撑能力差。反之，新能源机端电压跌落深，无功发出多，对主网支撑能力强，如图8所示。

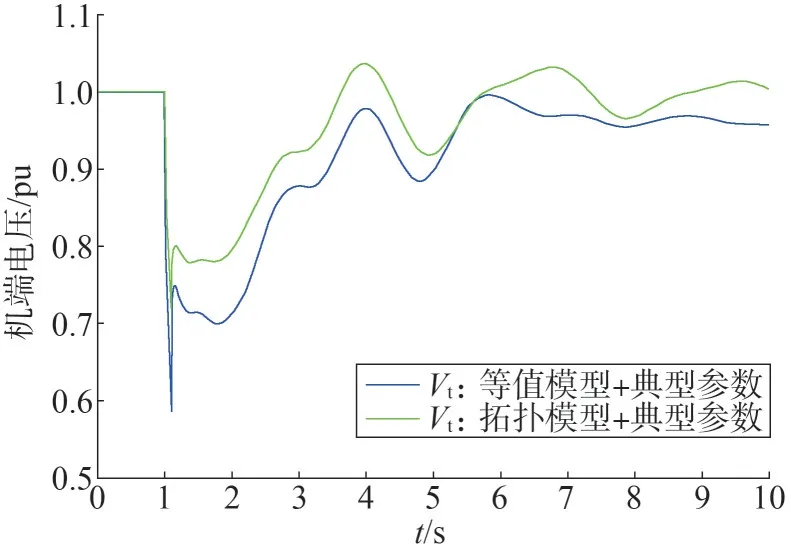
图7 不同拓扑建模DFIG机端电压对比

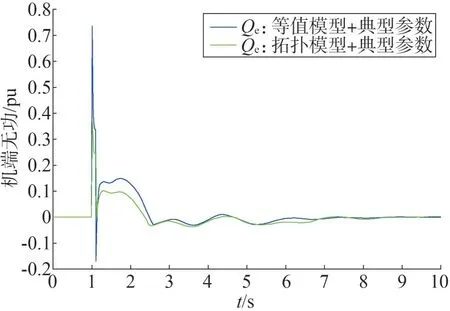
图8 不同拓扑建模DFIG机端无功对比

表3 某双馈风机无功典型控制参数

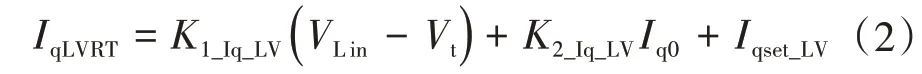
式中：IqLVRT为机组低压穿越运行时的无功电流分量；K1_Iq_LV和K2_Iq_LV为无功电流计算系数；VLin为进入低穿电压阈值；Iq0为初始无功电流；Iqset_LV为无功电流整定值。

拓扑模型精细化建模，新能源机端电压距离故障点电气距离远，因此故障后机端电压跌落少，对大电网的无功支撑能力差，等值模型接入的新能源机组距离大电网电气距离近，电压跌落深，因此无功支撑能力强，电压稳定性更好。

为验证网络结构对电压稳定性影响结论，摒除典型参数过于保守的影响，进一步采用拓扑模型+一套实测参数与等值模型+一套实测参数两种建模方法，对电压稳定性进行复核，其结果对比如表4所示。

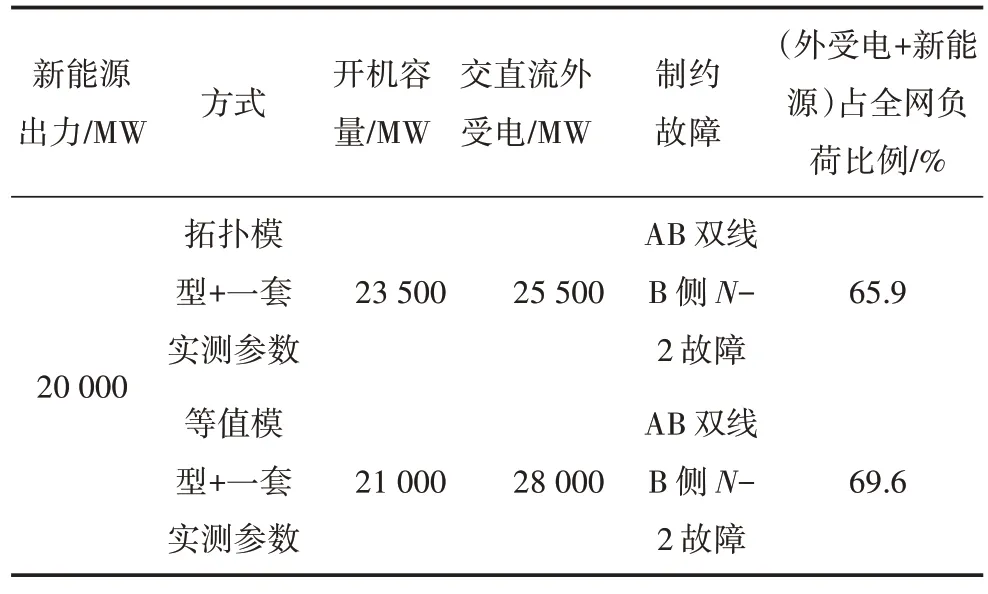
表4 拓扑建模差异下两种建模方法受电能力对比

可以看出，在全网新能源均采取一套实测参数情况下，维持原有规律不变。等值模型的电压支撑能力依旧强于拓扑模型，表明网架拓扑结构的建模会在计算中一定程度上影响电压稳定性。

5 结语

针对大电网数值仿真等值模型可能造成的计算不准确现象，提出了一种需求侧与新能源精细化建模方法，结合新能源实测建模与参数拟合工作，为新能源场站配套实测参数，以实现对新能源大规模接入后大电网暂态特性更加准确可靠仿真。仿真算例说明不同建模方法对电网电压稳定性影响。

采用精细化建模方法，提高了数值仿真的正确性，今后将在以下方面进一步研究：结合实际生活中居民负荷与工业负荷的不同特性，进一步对负荷精细化建模；由于电力电子大规模接入电网，使用机电、机电电磁混合与全电磁对结论进一步仿真，以相互佐证其正确性；结合数值仿真与直接法的优越性，对系统失稳的主导模式进一步定性研究，给出主导失稳因素的判断依据。