两级式光伏发电并网逆变系统

王 傲，张厚升，朱胜杰，靳 舵，蒋俊杰

（山东理工大学电气与电子工程学院，山东 淄博 255022）

0 引言

当今世界能源消耗量在逐年递增，对石油、煤炭等能源的大量使用，不仅会造成化石能源的局部性短缺，而且会给环境带来不可估量的危害，加大新能源发展力度势在必行［1-3］。太阳能作为一种清洁能源，其发电系统安装简便，可直接接入区域配电系统，在未来发电占比将越来越大。所研究的光伏并网发电系统具有结构简单、工作稳定和维修便捷等优点，适用于光伏建筑一体化的场合，尤其是家庭户用光伏发电［4-6］，既可满足自身的用电需求，在政府政策支持的情况下，还可将剩余的电量并入当地电网作为一种额外的家庭经济收入来源。

光伏（Photovoltaic，PV）并网逆变的核心问题是如何使光伏阵列工作在最大功率点以及如何实现并网电流和电网电压的同频同相。在最大功率点跟踪（Maximum Power Point Tracking，MPPT）各种算法中，扰动观察法（Perturbation and Observation Method，P&O）控制思路清晰、实现方便［7-9］，因此在工程上被广泛使用，但传统的定步长扰动观察法无法兼顾跟踪的速度与精度，会造成不必要的能量损失。后级电路采用电压电流双闭环控制，其中电流环常采用的比例积分（Proportional Integral，PI）控制往往难以实现电流的无静差跟踪［10-13］，控制效果不理想。

为改善上述问题，将基于电压寻优的变步长扰动观察算法与比例谐振（Proportional Resonant，PR）控制电流两种控制策略相结合，可有效实现光伏发电系统的最大功率跟踪及单位功率因数并网控制，最后通过仿真验证了所设计系统的可行性。

1 单相光伏并网逆变系统

两级式非隔离型光伏并网单相逆变系统如图1所示。

该系统基本原理为：首先前级升压电路对光伏阵列的电流Ipv和电压Upv进行采样，利用MPPT算法，使得输出电压不断向最大功率点处所对应的电压靠拢，将MPPT 模块参考电压与Upv的差值送入PI 调节器得到的信号与三角载波做比较，为升压斩波电路提供开关信号，使直流侧电压高于电网侧电压幅值；然后后级逆变电路采用双闭环控制，电压外环有两个作用，一是采用PI调节得到参考电流幅值Iref，同时由锁相环（Phase Locked Loop，PLL）得到相角θ，进而得到参考并网电流iref，二是使直流母线电压稳定于Uref。电流内环将iref与实际并网电流igrid的差值送入PR 控制器，其输出与电网电压ugrid的前馈信号叠加［14］，经正弦脉冲宽度调制（Sinusoidal Pulse Width Modulation，SPWM）调制驱动单相全控桥式逆变器以实现电流的无静差跟踪。

2 光伏逆变系统的控制

2.1 前级升压电路

前级电路的目标是通过Boost 电路升高光伏阵列的输出电压以满足直流母线电压高于电网电压幅值的要求，并且实现最大功率点跟踪。光伏阵列通过光电效应实现光能与电能两种形式的转换，但光伏阵列的输出电压与功率的关系并非是线性的，因此需要采取特殊的方法使系统工作在特定的电压或电流下。光照强度变化对光伏阵列输出功率的影响远大于温度变化对输出功率的影响，因此可忽略温度对PV阵列的影响，如图2 所示，选取某种型号的PV 阵列，在恒温25 ℃下，依次绘制出光照强度为1 kW/m2、0.5 kW/m2、0.1 kW/m2时的光伏特性曲线，从图中可以得知光伏阵列的输出功率随电压的增加呈现出先增后减的趋势，且增加的趋势较慢，减小的趋势较快，在该过程中存在一个最大输出功率点A（jUAj，PA）j，其中j=1，2，3。MPPT 算法的最终目的就是使光伏阵列始终处于所期望的最大功率工作状态上。由于外部环境不是一成不变的，因此，扰动观察法的实现需要不断对光伏阵列电压U、电流I信号进行采样，得到功率P，通过计算当前工作点与上一工作点的功率和电压差值，若两者符号相同则应增大电压，反之应减小电压，然后循环该过程直至到达最大功率点。

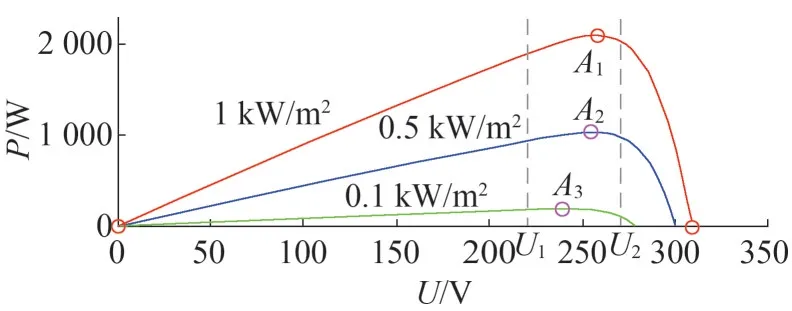
图2 光伏阵列特性曲线

在系统运行过程中，只采用同一步长往往很难直接精确对最大功率点进行跟踪，如果步长过大甚至会越过最大功率点，出现幅值震荡问题影响跟踪精度，而仅是采用较小步长势必会影响跟踪速度。为改善该问题，提出了一种变步长扰动观察法，在某一时刻，首先分别观测电压、功率与上一时刻的差值，判断出该时刻在最大功率点左侧还是右侧，这一步实质上是由功率对电压导数的正负确定当前时刻工作点的所在。以图2 为例，假设一天内的最大光照强度 为1 kW/m2，最 小 为0.1 kW/m2，定 义U1＜UA3，U＞2UA1。因此可将图2分为两部分，第一部分包含所有光照强度下所对应的最大功率点，即U1＜U＜U2；第二部分为相对远离最大功率点的位置，即U＜U1或U＞U2。若采样所得的U在第一部分内，则采用较小步长d2进行小幅度扰动，反之则采用较大步长d1进行扰动。该方法既保证了最大功率点的跟踪速度和精度，又减少了能量的损失，变步长扰动观察法控制如图3所示。

图3 变步长扰动观察法控制

2.2 后级电流内环电路

电流内环的主要功能是使逆变器输出电流跟踪指令信号iref以保证igrid与ugrid同频率且同相位，电流内环控制如图4 所示。其中采用双极性SPWM 调制的逆变单元可等效为小惯性环节，即

图4 电流内环控制

式中：KPWM为逆变器增益；Ts为惯性环节时间常数。

滤波器的传递函数为

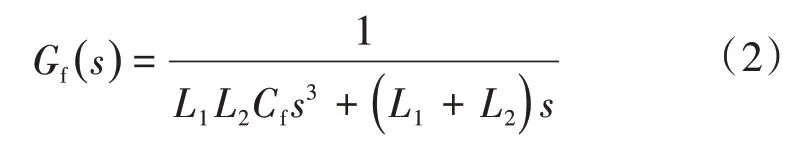
式中：L1、L2为滤波电感；Cf为滤波电容。

对控制器的传递函数及相关参数进行分析。若采用传统的PI调节无法实现对电流信号的无静差控制，对高频信号的跟踪性能及抗干扰性能较差，而采用PR 控制可以较好改善该类问题。理想PR 控制器的传递函数为

式中：kp为比例系数；kr为谐振系数；ω0为基波频率，电网频率取为50 Hz，因此ω0=2πf=314 rad/s。

理想PR 控制器仅可实现对特定频率下的正弦信号的跟踪，而对其他频率下的正弦信号作用微乎其微，且在特定频率处趋近无穷大的增益可能影响系统的稳定性。另外，在系统实际运行过程中，可能由于电网频率的波动或测量采样的不精确性而导致PR 控制器抗干扰性能下降。因此，进一步利用准比例谐振控制来替代上述理想PR控制，其传递函数为

式中：ωc为截止频率；ω0为已知量；需要控制的参数为kp，kr和ωc。

首先，计算参数ωc。若固定kp和kr，只改变ωc的值，控制器的带宽与各频率（不含ω0）的增益都会随着ωc的增大而增大。由带宽定义可求得该系统带宽为ωc/π［15-16］，设电网频率波动偏差为±0.5 Hz，可求得ωc的最小值为3.14 rad/s。

其次，确定参数kr。若固定kp和ωc，仅改变kr的值，PR 控制器的带宽无变化，而控制器各频率的增益随着kr的增大而增大。在选择kr时，若kr值过大，会连同远离基波频率的谐波分量也一起放大；若kr值过小，无法保证ω0附近的频率留有足够的增益。因此，kr应根据实际情况适当选择。

最后，确定参数kp。若固定kr和ωc，仅改变kp的值，随着kp的增加，各频率处的增益在增加，但基波频率处的幅值增加的幅度不大。比例项的设置会影响系统的动态性能，kp增加，系统的震荡次数与调节时间也会随之增加。

2.3 后级电压外环电路

电压外环的第一个功能是稳定直流母线电压Udc，控制逆变器直流侧电容的电压稳定即可实现光伏阵列产生的能量与并网能量之间的平衡。

电压外环的第二个功能是为电流内环提供电流指令值iref。在得到与并网电压同频同相的参考电流iref的过程中，其必不可少的一环为锁相环功能的实现。通过检测每个工频周期内电网电压的过零点来实现锁相是工程上被广泛应用的一种锁相技术，但在电网电压因谐波而产生畸变或者检测电路因各种干扰而无法精确工作等情况下，会对过零点的检测造成困难，限制了锁相精度和速度。

为了更好地实现锁相功能，在三相电网电压单同步坐标系软件锁相环的基础上［17-19］，对基于虚拟坐标变换的单相电网电压锁相方法进行了分析。首先以已知的电网电压ugrid为基础，构造出比其滞后90°的正交电压，分别作为两相静止坐标系下的α轴分量uα、β轴分量uβ，然后由两相静止坐标系与旋转正交坐标系间的变换得到dq坐标系下的d轴分量ud和q轴分量uq。接下来对单同步坐标系软件锁相环进行研究，单同步锁相环电压矢量如图5 所示，若想实现锁相功能，令电网电压矢量ugrid与ud同向即可。当ugrid在q轴上的投影小于零时，ud将超前于ugrid；当ugrid在q轴上的投影大于零时，ud将滞后于ugrid；那么只有当ugrid在q轴上的投影等于零时，才能使得两个电压矢量重合。因此，控制uq为零就可使锁相环输出电网电压相位即ωt=θ。单相锁相环的实现如图6所示。

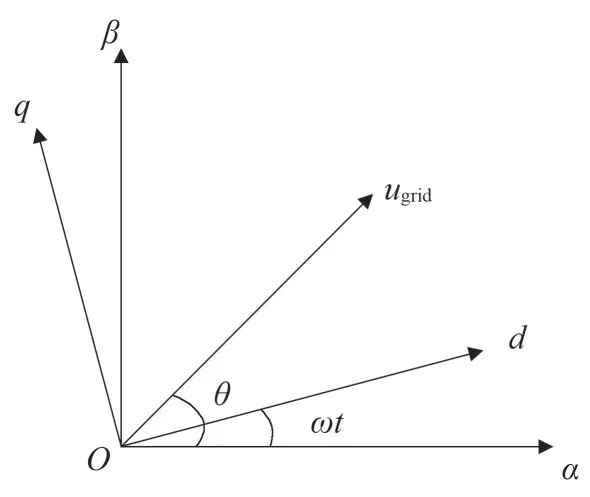
图5 单同步锁相环电压矢量

图6 单相锁相环实现

3 仿真分析

为验证所设计的两级式非隔离型光伏并网单相逆变系统的工作效果，按照上述方法在MATLAB/Simulink中搭建了相应的仿真模型。并网电压有效值为220 V，频率为50 Hz。

首先，验证前级升压电路是否能达到预期。光伏阵列由Simulink 工具箱中的PV Array 实现，在Module 选项中设定光伏阵列的型号，设置固定外部环境光照强度1 kW/m2以及温度25 ℃，此时光伏阵列的开路电压也即最大工作电压为309 V，当工作电压为258 V 达到最大功率2 097.54 W，MPPT 变步长扰动观察法使用MATLAB Function 模块编程实现。光伏阵列的输出功率曲线如图7 所示，在0.13 s 左右系统稳定在最大功率点附近，在传统扰动观察法的基础上，既达到了最大功率跟踪的目的，又提高了系统的响应速度。

图7 光伏阵列输出功率曲线

其次，验证对后级逆变电路电压电流双闭环的分析与研究正确与否。单相锁相环工作情况如图8所示，该环节在极短的响应时间内就对电网电压频率和相位完成了锁定。直流母线电压波形如图9 所示，在0.13 s左右即稳定在区间［397，403］内，波动幅度很小基本满足设定值400 V。并网电流与参考并网电流波形如图10 所示，在0.13 s 后两者波形基本重合，实现了并网电流igrid对参考指令电流iref的无静差跟踪。

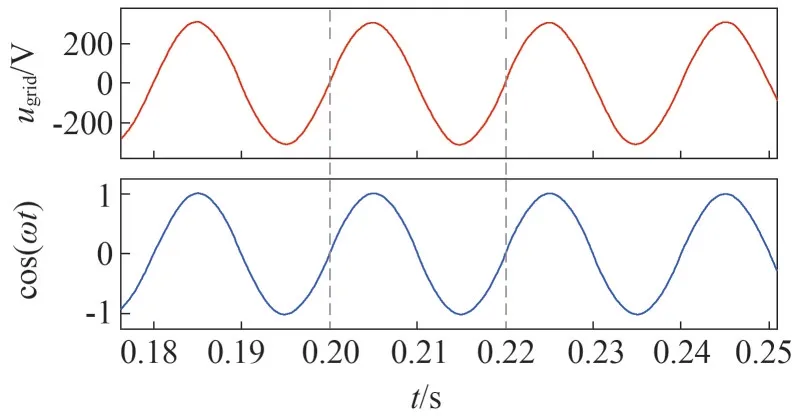
图8 单相锁相环工作情况

图9 直流母线电压

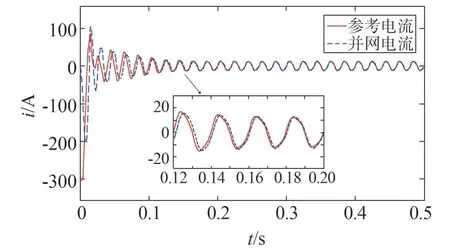
图10 并网电流与参考并网电流波形

最后，比较PI 控制与PR 控制下的并网电流波形。其中PI 控制的积分系数ki=50，比例系数kp=8.5；PR 参数为ki=8.5，kr=50，ωc=3.14。电网电压与并网电流的波形如图11 所示，两种情况都可快速达到稳态，但图11（a）PI 控制下，并网电流与电网电压之间存在较大的相位差，在图11（b）中PR 控制下两者的相位差极小，且此时电流畸变率为1.39%。PI、PR 控制器伯德图如图12 所示，由图12 也可看出，在基波频率处PR控制器的增益远远高于PI控制器的增益，因此PR控制下的电流波形有更好的品质。

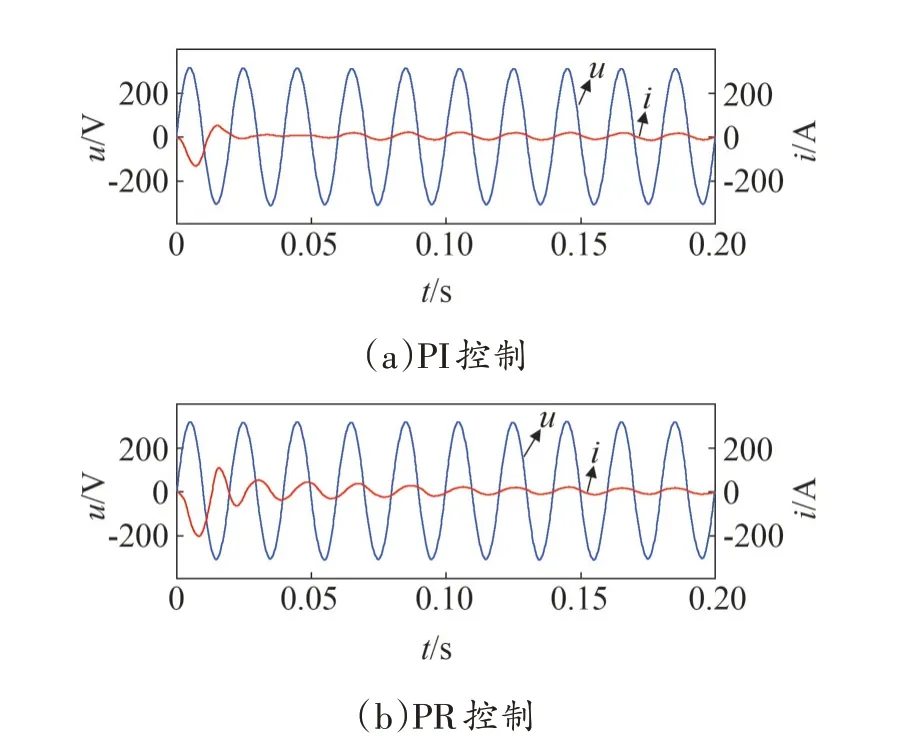
图11 并网电流与电网电压

PR 控制下电网频率波动时的并网电流与电网电压的波形如图13 所示。由图可知，并网电流能够很好对电网电压进行跟踪，且图13（a）中并网电流畸变率为2.54%，图13（b）中并网电流畸变率为3.21%，达到了预期效果。由图12 可分析得，在PR 控制下，基波频率附近也有着较大的增益，因此可以较好的应对电网频率小幅度波动的情况。

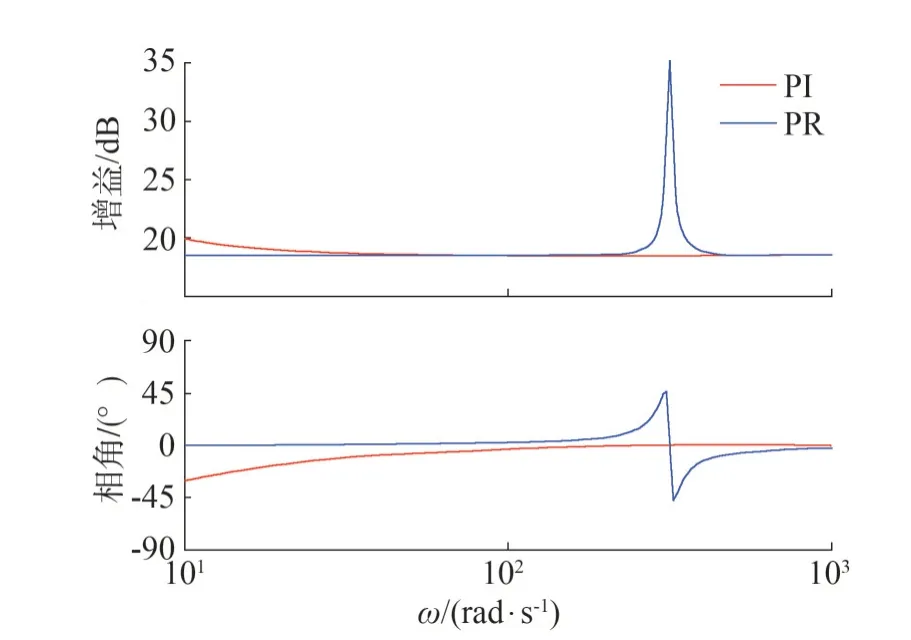
图12 PI、PR控制器伯德图

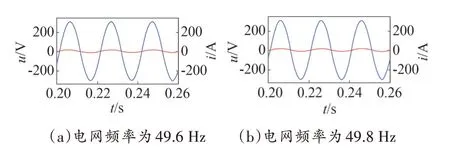
图13 频率波动时电网电压与并网电流波形

4 结语

主要研究了双级式单相光伏并网逆变系统的控制策略，前级升压电路运用变步长扰动观察法，结果表明可较快的对最大功率点进行跟踪；在后级逆变电路的分析中，锁相环的设计仿照单同步坐标系软件锁相环算法在三相逆变电路中的应用，采用构造虚拟正交分量及坐标变换的方法，实现了电网电压相位的快速锁定。电流内环中准比例谐振控制器的运用既可实现基波频率的无差跟踪，也可使系统在电网电压频率小幅度波动时仍能保证并网电流无静差跟踪参考电流。最终所设计系统实现了并网电流与电网电压的同频同相，满足并网运行要求，对于家庭户用光伏发电系统具有较好的实用意义。