大型M-矩阵Sylvester方程的分而治之方法
2022-06-03高艺萌王卫国
高艺萌, 王卫国
(中国海洋大学数学科学学院, 山东 青岛 266100)
本文主要考虑Sylvester矩阵方程
AX+XB=C,
(1)
其中A∈Rn×n,B∈Rm×m,C∈Rn×m,且系数矩阵满足下列条件之一:
(Ⅰ)A,B是非奇异M-矩阵,C≥0;
(Ⅱ)A,B是不可约M-矩阵且其中至少有一个是非奇异矩阵,C≥0。
方程(1)称为M-矩阵Sylvester方程(MSE)[1]。当系数矩阵没有结构要求时,称为一般的Sylvester矩阵方程;当A=BT时,称为Lyapunov矩阵方程。此类广泛应用控制理论领域[2],海洋平台减振系统中反馈增益模型需要求解Sylvester方程[3]。
求解方程(1)的常用数值算法有不动点迭代法[1,4]、牛顿法[2]、交替方向加倍算法[5]、子空间迭代法[6]和保结构加倍算法[2]等。当系数矩阵A,B阶数n,m很大时,MSE的求解速度会非常慢,且占用大量内存。P. Benner等针对大型矩阵代数Riccati方程,结合牛顿法和交替方向隐式迭代的思想提出了低秩牛顿交替方向法[7];D. Kressner等针对线性矩阵方程在低秩情况下提出了简单而快速的数值方法,基于这种思想,对系数矩阵具有特定的低秩分级结构提出了分而治之方法[8]。
本文将考虑系数矩阵具有分级非对角低秩(Hierarchically off-diagonal low-rank,HODLR)结构M-矩阵Sylvester方程,提出了分而治之方法,把方程化为低阶MSE和低秩MSE分别求解。具体思路如下:
设矩阵A,B,C可以分裂为
A=A0+δA,B=B0+δB,C=C0+δC,
(2)
其中δA,δB,δC是低秩矩阵。假设X0是矩阵方程
A0X0+X0B0=C0
(3)
的解,求δX使得X=X0+δX是方程(4)的解。
A0+δAX0+δX+
X0+δXB0+δB=(C0+δC)
(4)
由式(3)和(4)得
(5)


故式(5)是右端矩阵为低秩矩阵的方程,当式(5)是M-矩阵Sylvester方程时,我们简称为更新MSE问题。当式(3)中已知矩阵都是块对角阵时,式(3)将转化为多个低阶MSE问题的求解。
注1求解方程(1)转化为求解方程(3)和(5)。
1 M-矩阵及相关性质
本节主要介绍M-矩阵的定义与性质,以及对应的矩阵方程的可解性。
定义1[1]设A∈Rn×n,如果所有非对角元素都小于等于0即对∀i≠j,aij≤0,称A是Z-矩阵。如果存在数s和非负矩阵N,使得A=sI-N且s≥ρ(N),就称矩阵A是M-矩阵。当s>ρ(N)时,称A是非奇异M-矩阵;当s=ρ(N)时,称A是奇异M-矩阵。
关于M-矩阵有如下性质:
引理1[1](Ⅰ)设A是Z-矩阵,且存在v≥0,使得Av≥0,则A是M-矩阵;
(Ⅱ)M-矩阵的主子矩阵仍然是M-矩阵;
(Ⅲ)如果A是非奇异M-矩阵,且Z-矩阵B满足B≥A,则B是非奇异M-矩阵;
(Ⅳ)如果A是不可约奇异M-矩阵,且Z-矩阵B满足B≥A,当B≠A时,则B是非奇异M-矩阵;
(Ⅴ)如果A是非奇异的M-矩阵或不可约奇异M-矩阵,分块如下:
其中A11和A22是方阵,则A11和A22都是非奇异的M-矩阵。
引理2[1]设A∈Rn×n是Z-矩阵,则下列几个命题等价:
(Ⅰ)A是非奇异M-矩阵;
(Ⅱ)A-1≥0;
(Ⅲ)存在v∈Rn满足v>0,使得Av>0;
(Ⅳ)A的全部特征值都有正的实部。
关于矩阵方程(1)有如下定理。
定理1(Ⅰ)设A和B都是非奇异M-矩阵,且C≥0,则方程(1)存在唯一非负解。
(Ⅱ)设A和B是不可约M-矩阵且至少一个是非奇异矩阵,C≥0,则方程(1)存在唯一非负解。
证明 由A和B是非奇异M-矩阵或是不可约M-矩阵且至少一个是非奇异矩阵,可得
P=Im⊗A+BT⊗In
是非奇异M-矩阵,因此方程(1)有唯一解。
由引理2中(Ⅱ)得P-1≥0,注意到C≥0,所以解是非负的。
定义2[8]若A∈Rn×n,分裂p层记为Γp,则:
(Ⅰ)对于k∈N,称A为Γp,k)-HODLR矩阵当且仅当每一个非对角块A(Ili,Ilj)和A(Ilj,Ili)的秩不超过k,其中i,j={2,1,4,3,…,(2l,2l-1)},l=1,2,…,p。
(Ⅱ)对于Γp,矩阵A的HODLR秩指:最小正整数k使得A是Γp,k)-HODLR矩阵。
2 低秩更新
本节主要考虑矩阵C是非负低秩时,MSE的求解方法。对于系数矩阵是小型矩阵或稠密矩阵情形,已有多种求解算法,例如矩阵分解法、Hoskins迭代法、交替方向法等[2]。文献[4]中提出了Smith方法,但Smith方法中的参数不易选择,文献[9]提出了求解MSE方程的交替方向Smith方法(Alternating directional Smith method,ADSM),迭代序列是非负单调上升的,且平方收敛。ADSM是Smith方法的改进。具体算法如下:

算法1[9] :ADSM(A,B,C) % 求解AX+XB=C1.令α=max1≤i≤naii, β=max1≤i≤mbii。2.计算 E0=(B-βI)(B+αI)-1, F0=(A+βI)-1(A-αI), X0=(α+β)(A+βI)-1C(B+αI)-1。3.对k=1,2,…,重复下列步骤直到矩阵序列Xk收敛 Xk+1=Xk+FkXkEk, Ek+1=E2k,Fk+1=F2k。
对于方程(5),给定如下形式的低秩分解
则
式中U,V均为低秩且令
s=rank(δA)+rank(δB)+rank(δC)。
则方程(5)可以表示为:
AδX+δXB=UVT。
(6)
式中:A=A0+δA,B=B0+δB,U∈Rn×s,V∈Rm×s,s≪min{n,m}。低秩近似解Xk=Zk(Yk)T可以直接利用低秩ADI方法求得[5,10],但迭代中的参数需要事先给定,且最优参数不易获得。本文将使用文献[8]中的扩展Krylov子空间方法,此类算法不需要事先选定参数。基本思路是利用块Arnoldi过程得到扩展Krylov子空间:
Ut:=εKt(A,U)=
{U,A-1U,AU,A-2U,…,At-1U,A-tU},
Vt:=εKt(BT,V)=
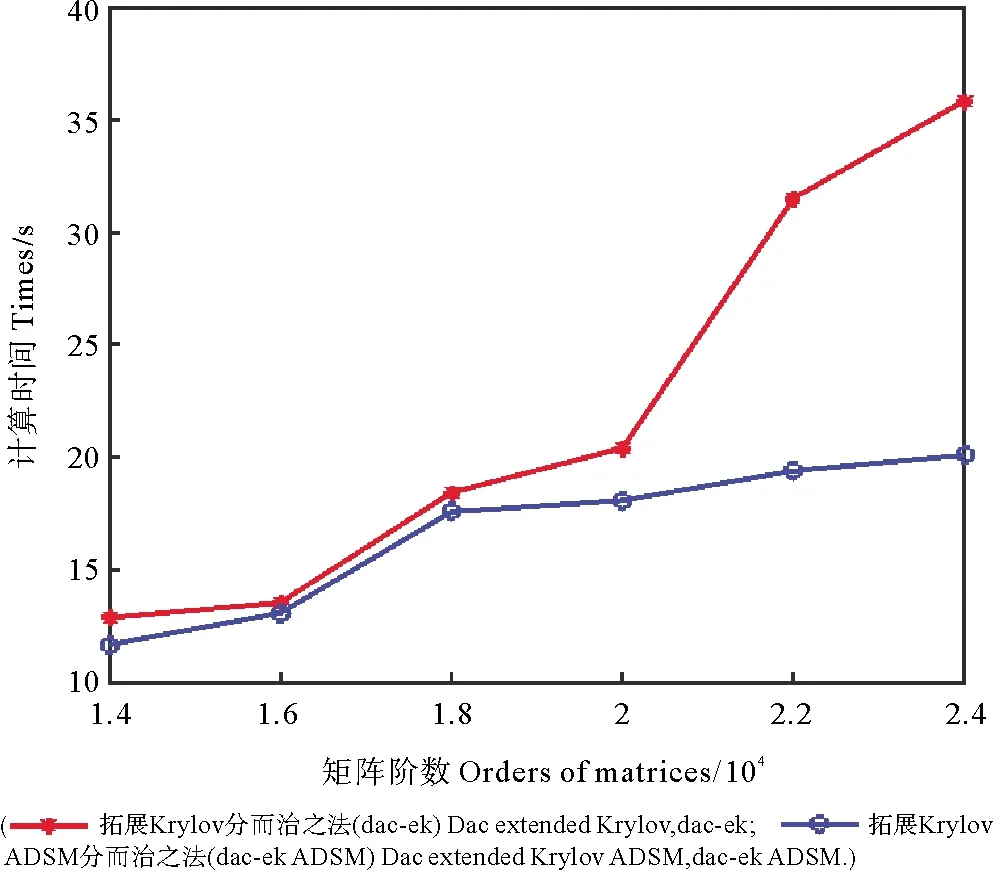
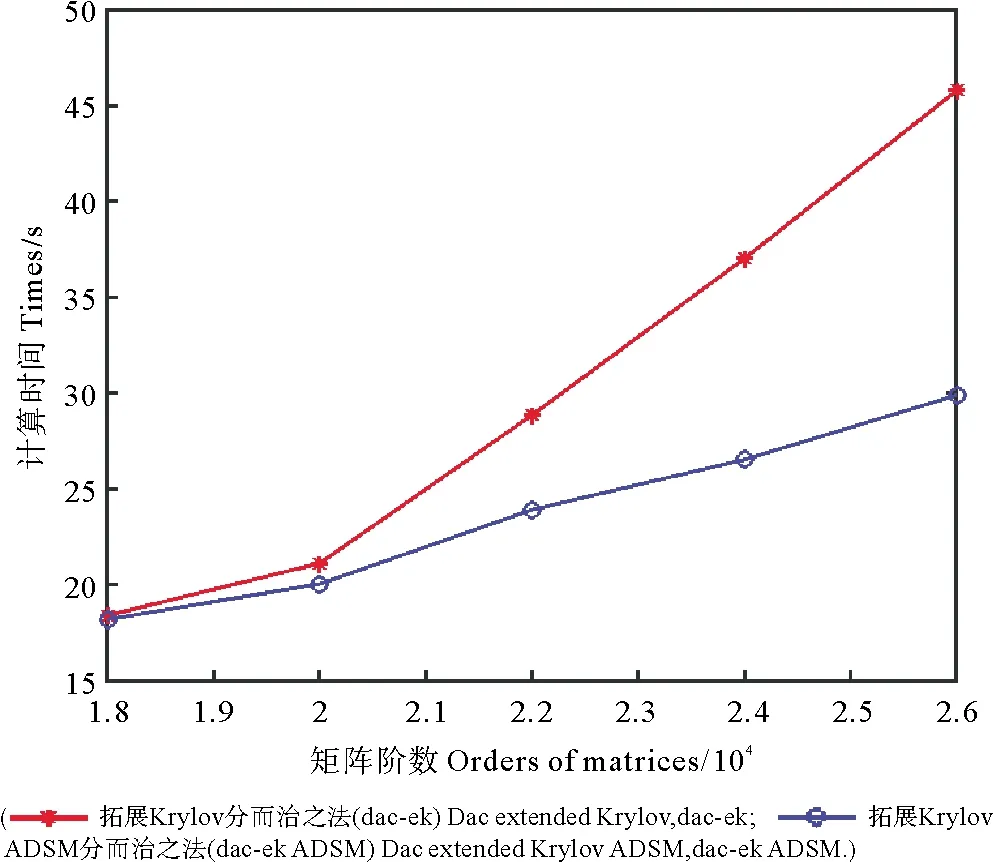
式中2ts 具体算法如下: 算法2 [8]:LRMSE(A,B,U,V) %求解AδX+δXB=UVT1.U1,- =qr(U,A-1 ),V1,- =qr(V,B-1 )。2.对k=1,2,…, 计算 A=UTkAUk,B=VTkBVk,C=UTkUVTVk, Xk←利用稠密方法计算AXk+XkB=C的解, 判断Xk是否收敛,如果收敛,令 X=UTkXkVk,停止。 否则,令 Uk=U0,U+,U- , Vk=[V0,V+,V-], 计算 U=[AU+,A-1U-], V=[BV+,B-1V-], U←U-UkUTkU, V←U-VkVTkV, U,- =qrU , [V,-]=qr(V), Uk+1=[Uk,U], Vk+1=[Vk,V]。 设方程(1)的系数矩阵具有分级非对角低秩矩阵结构,首先进行如下分裂: A=A0+δA,B=B0+δB,C=C0+δC。 (7) 式中:A0,B0,C0是块对角矩阵;δA,δB,δC是低秩矩阵;此时方程(1)可化为方程(3)和(5)。当对角块矩阵仍具HODLR结构时,将递归地进行分裂。具体递归分裂的层数将根据矩阵的HODLR结构、计算机的存储能力和计算速度确定,相关内容见文献[11]。图1 展示了HODLR结构,对角块黑色部分为低阶矩阵,其余为低秩矩阵。具体如下: 图1 HODLR形式[8]Fig.1 HODLR form [8] 式中:A12,A21为低秩矩阵,A11,A22仍具有HODLR结构特征,对主对角块矩阵继续分裂,直至最小块阶数满足要求后停止。 设方程(1)的系数矩阵A,B,C都是HODLR矩阵,则类似文献[8],得出MSE的分而治之方法。对系数矩阵进行如下分裂: (8) 式中: 类似地分裂B和C: (9) (10) 注3分块后的子矩阵需要保证对应的矩阵方程有意义。若对角块Aii,Bii,Cii,i=1,2仍是HODLR矩阵,则继续进行分裂。低秩部分对应的更新MSE的近似解将用低秩算法求解,如Krylov子空间方法、 低秩Smith法、低秩ADSM法等。若每一递归层均有唯一的非负解,则方程(1)有唯一的非负解。 下列定理可以保证解存在唯一性。 定理2设A和B是非奇异M-矩阵或是不可约M-矩阵且至少一个是非奇异矩阵,C≥0,矩阵分裂由方程(8)、(9)和(10)得到,则下列结论成立: (Ⅰ)矩阵方程 AiiXii+XiiBii=Cii,i=1,2 (11) 是M-矩阵Sylvester方程,且有唯一非负解X11,X22,即X0=diag(X11,X22)≥0是式(3)的非负解; (Ⅱ)此时得到的矩阵方程(5)是M-矩阵Sylvester方程,且有唯一非负解δX; (Ⅲ)方程(1)的非负解为X=X0+δX; (Ⅳ)分裂k次时解为 其中, 证明 (Ⅰ)由引理1中(Ⅴ)可知,A11,B11,A22,B22都是非奇异M-矩阵。由分裂方程(10)可知C11,C22都是非负矩阵,所以方程(11)是MSE,故有唯一非负解。 故公式(5)是M-矩阵Sylvester方程,且有唯一非负解δX。 (Ⅲ)由(Ⅰ)、(Ⅱ)证明可知(Ⅲ)成立。 (Ⅳ)由(Ⅰ)~(Ⅲ)知,当k=1时成立。 k=2时,原方程的解为 设第k-1次分裂时,原方程的解也满足 定理3在定理2条件下,且A,B,C具有HOLDR结构,则递归层对应的矩阵方程都是M-矩阵Sylvester方程。 证明 由引理1中(Ⅱ)可知,A和B的对角块子矩阵都是非奇异M-矩阵。从而A和B的非对角块子矩阵都是非正矩阵,C≥0,由定理2可得结论成立。 下面给出求解MSE的分而治之方法。 算法3 DACMSE(A,B,C) % 求解AX+XB=C1.给定A,B,C。2.当A,B,C具有HOLDR结构时,分块。3.A=A1100A22+UAVTA,B=B1100B22+UBVTB, C=C1100C22+UCVTC。4.Xii←DACMSE(Aii,Bii,Cii),i=1,2。5.令X0=X11X22。6.令U=[UC,-UA,-X0UB],V=[VC,XT0VA,VB]。7.利用低秩算法求解δX←LRMSE(A,B,U,V)。8.返回:X0+δX。 在本节中,我们通过数值算例来比较两种不同分而治之法求解MSE的效果。基于工具包hm-toolbox[11]在MATLAB2019b运行所有算法。相对误差如下: 例1 系数矩阵分别为: 我们设置最小块阶数不超过100,分别使用拓展Krylov分而治之方法(dac-ek)和拓展Krylov ADSM分而治之方法(dac-ek ADSM)求解,从表1 可知dac-ek ADSM在时间、精度方面均得到改进,随着阶数的增大,计算时间节省。图2是求解不同阶数MSE的计算时间。 表1 求解不同阶数下MSE的计算时间与相对误差Table 1 The times (in seconds) and relative residuals for the algorithms applied to the different orders matrices equations 图2 求解不同阶数MSE的计算时间Fig.2 The times (in seconds) for the algorithms applied to the different orders matrices equations 例2 系数矩阵为随机带状M-矩阵, x=randn-1,1, A=2eye(n)-diag(x,-1)-diag(x,1), B=2AT, C0=diag(rand(n,1))+diag(x,-1)+diag(x,1), UC=rand(n,2),VC=eye(n,2), 图3表明拓展Krylov ADSM分而治之法比拓展Krylov分而治之法计算速度更快。 图3 求解不同阶数MSE的计算时间Fig. 3 The times (in seconds) for the algorithms applied to the different orders matrices equations 本文给出求解大型M-矩阵Sylvester方程化为低阶方程和低秩方程分别求解的分而治之算法,证明了递归层对应的低阶方程和低秩矩阵方程都是M-矩阵Sylvester方程。数值实验表明本文提出的算法对大型M-矩阵Sylvester方程有效。


3 分而治之法

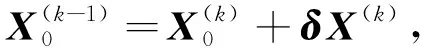
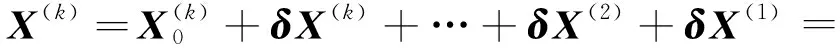

4 数值算例

5 结语
