导管桨近水平壁面流场特性DDES模拟
2022-06-03郭子康刘永辉赵昌宇
张 嶔, 郭子康, 刘永辉,2, 赵昌宇, 许 情
(1. 中国海洋大学工程学院, 山东 青岛 266100; 2. 中国海洋大学实训中心, 山东 青岛 266100)
导管螺旋桨(导管桨)是船舶常采用的一种推进方式,其结构由外围环形导管和螺旋桨组成,导管的导流作用能增加推力,提高推进效率以满足航行需要,同时导管桨还有重载状态下工作效率高、操作性好、受海况变化影响小等优点。作为轨迹与姿态操纵的主动控制装置,导管桨越来越多地应用于船舶、水下航行器及海洋平台动力定位系统中。但由于受到船壳(浮筒)壁面等因素影响,导管桨的有效推力远小于敞水推力。且由于入流条件的不断变化(如动力定位),导管桨形成的流场极易产生船体振动及噪声和水下辐射噪声,影响和干扰船员和船载水下勘探等,且近年来由于推进器尾流而引起的港池或航道内的局部冲刷已经成为导致港池结构物不稳定甚至破坏的主要原因之一。因此对于导管桨与近壁面之间相互作用机理的研究是十分有必要的。
现阶段已经有许多学者进行了关于船舶推进器对于壁面影响的相关研究,而对于水下航行器中导管桨的研究多集中于具体实际工程问题[1-2],对壁面影响规律的研究并不系统。Bergh等[3]调查瑞典18个港口中有16个有螺旋桨导致的海床局部冲刷。Qurrain[4]指出英国有42%的港口受推进器尾流冲刷影响。Tsinker[5]提出港口设施及海床需要进行一定程度的保护措施以应对船舶推进器产生的冲刷。de Gijt等[6]发现船舶推进器导致的海床底部局部冲刷坑有数几米深。国内河海大学和天津大学也正进行此领域的探索性研究。这些问题的结果都说明了随着船舶推进马力的不断加大,螺旋桨及推进器转动时所产生的尾流速度、强度和影响范围不断加大。而船舶吃水加深进一步导致码头、护岸、边坡等港口设施产生淘刷现象。在航道上,海床受推进器冲刷影响导致局部冲刷和淤积,使得海床高低起伏不平,进而影响船舶航行安全。传统上对此现象的研究集中于推进器尾流引起的冲刷深度及冲刷过程的探究[7-9]把推进器尾流简化为射流,且以物理模型试验为主。荷兰MARIN于2008年开始了一项导管桨水动力企业联合研发项目(Thrust hydrodynamics joint industry project, TRUST JIP),项目针对导管桨尾流进行了一系列物理模型试验研究。为了研究导管桨与壁面间的相互影响,Cozijn等[10]在TRUST JIP项目中进行了导管桨在水平壁面下的物理模型试验,使用stereo PIV观测了导管桨尾流受水平壁面影响下的变化。物理模型试验仅进行了系泊状态下(J=0),导管桨无倾斜和7°倾斜的两组试验,其中只有无倾斜状态下导管桨尾流PIV测量数据公开发表。新加坡南洋理工大学Yee-Meng Chiew教授团队对于推进器尾流引起淘刷现象的冲刷深度及冲刷过程进行了一系列物理模型试验研究[7,11-13]。数值模拟方面的研究相对较少,并主要以RANS紊流模型模拟为主[14-15]。对于导管桨在港池壁面(水平、竖直及倾斜壁面)影响下的尾迹流场,未见有相关研究。
综上所述,本文将采用滑移网格与DDES模型相结合的方法,并延用上述MARIN研发项目的物理模型,在进速系数J=0和J=0.4、桨倾角β=0°和β=7°这4种工况下对导管桨近壁面流场进行分析,得到导管桨与近壁面流场特性,总结导管桨在水平壁面条件下尾流涡的发展和消散规律,为解决导管桨等船舶推进器引起港池冲刷现象提供一定的理论支撑。
1 数值计算模型
1.1 研究对象
数值模型为三维黏性不可压缩的紊流数值计算模型,数值计算所用的导管桨模型参照Cozijn和Hallmann研究的四叶导管桨[16],由桨毂,四片桨叶,导管以及推杆组成,螺旋桨型号和导管型号分别是5810R和1393,桨直径为0.1 m,螺距比为1。
1.2 数值计算方法
纳维-斯托克斯方程(Navier-Stokes equation)是描述黏性不可压缩流体动量守恒的运动方程:
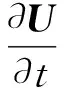
(1)
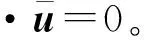
(2)
由于紊流是一种无规律、不规则、非定常、三维、非线性和不可逆的流体现象,所以对工程实际中高雷诺数流场的研究非常困难。虽然紊流运动十分复杂,但流体依然遵循连续介质运动的特征和基本力学规律,而且工程实际应用的要求至少能给出流场、压力等参数的平均值,故Reynolds-Averaged Navier-Stokes(RANS)方程可以将速度、压强等紊流瞬时物理量分解为平均值和波动值,然后将瞬时的波动值通过时间平均的方程体现出来,从而避免了直接数值模拟巨大的计算量,而且也能够满足工程实际应用的需要。
基于RANS理论,流场中任意一点的速度和压力可以分解为:

(3)
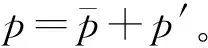
(4)
将式(3)和式(4)带入Navier-Stokes方程中
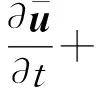
(5)
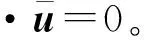
(6)
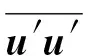
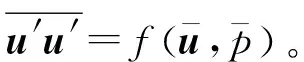
(7)
Large Eddy Simulation(LES)即大涡模拟将Navier-Stokes方程通过一定的尺度过滤,小于这一尺度的涡量通过计算求解,而大尺度的紊流和对应的流场进行直接数值模拟,从而能在紊流中捕捉到更多的流场细节。
为了解决由网格密度引起的近壁面处模拟应力耗尽的问题,Spalart, Deck在标准DES模型的基础上开发了DDES模型。DDES模型通过涡流黏性检测边界层的位置,并强制边界层内的流场由RANS方法求解。
SpalartAllmarasDDES紊流模型中rd的求解公式为:
(8)
式中:Ui,j是速度梯度;rd在对数边界层中等于1,在靠近壁面的过程中逐步降到0。
fd≡1-tanh8rd3。
(9)
fd在LES区域(rd≪1)等于1,则
(10)
当fd=1时DDES模型即为DES模型:
(11)
带滑移网格的DDES模型结合了RANS模型和LES模型,因而兼有RANS模型和LES模型优点,可用于求解导管桨非定常三维湍流场。但由于滑移网格DDES模型对计算资源和计算耗时偏高。本文将首先进行定常数值模拟,在定常数值模拟基础上进行非定常数值模拟,并与物理模型试验对比,验证计算模型精度。首先,利用多旋转参考系MRF(Multiple Reference Frame)模拟叶片转动,应用Spalart-Allmaras紊流模型获得导管桨的定常结果;其次,将此结果作为初始流场,进行非定常RANS数值模拟计算直到流场稳定,从而获得基于Spalart-Allmaras紊流模型的非定常流场结果。然后,开启基于Spalart-Allmaras紊流模型的DDES高精度数值模拟计算,直到流场稳定;最后,开始记录保存导管桨旋转至少10圈的流场及相关力数据,用于后续分析。
1.3 计算域与边界条件
计算域设置如图1所示,计算域长为25D(与物理模型平板长度一致,其中D为螺旋桨直径,见图2)、宽12D、高12D的矩形,上壁面为无滑动壁面条件,左为入流边界,右为出流边界,其余面为对称边界。
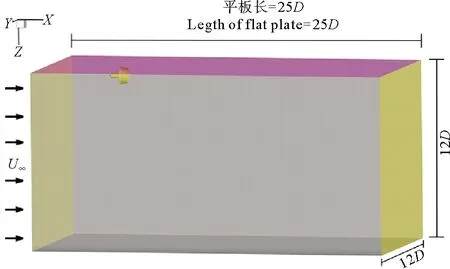
图1 数值模拟计算区域Fig.1 Numerical simulation calculation area

图2 MARIN JIP物理模型试验设置Fig.2 Marin JIP physical model test setup
1.4 网格划分和工况设定
为了验证JIP物理模型试验并模拟水下航行器倾斜导管桨条件,本文将对进速系数为J=0和J=0.4的导管桨水平和7°倾斜共4种工况,进行基于延迟分离涡模拟和滑移网格相结合的非定常尾涡演化数值模拟,工况设定如表1所示。
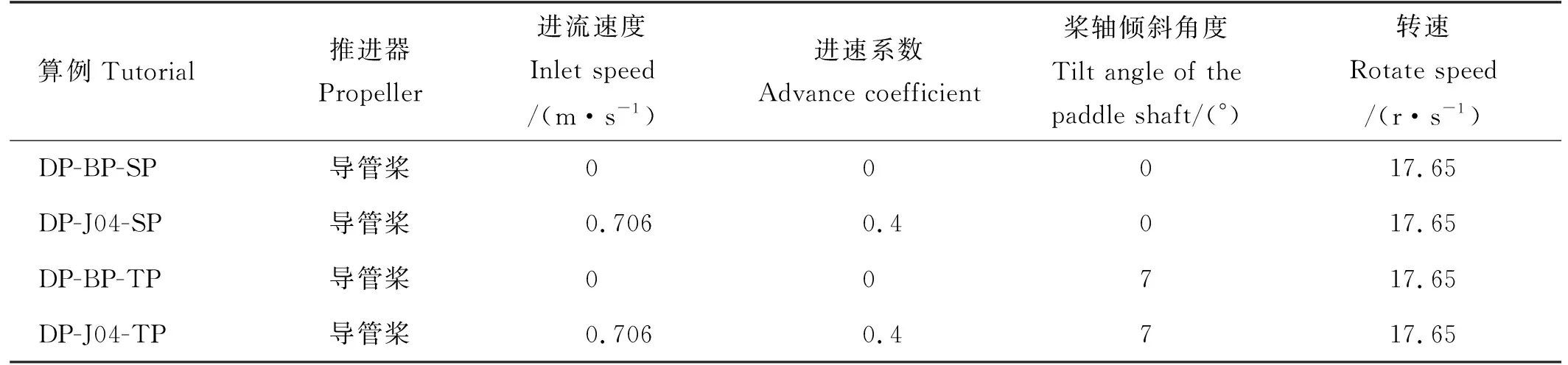
表1 算例工况设定Table 1 Example working condition setting
为了保证计算精度和计算效率,整个计算域全部由结构化网格构建,如图3所示,导管桨无倾斜算例的整个计算域总网格量为4.82×107,导管桨7°倾斜算例的整个计算域总网格量为4.53×107。基于非定常RANS数值模拟计算获得的初始化流场,水平壁面最大yplus为0.3,小于1,所用壁面网格密度可以保证计算精度。

图3 数值模拟全结构化网格Fig.3 Fully structured grid for numerical simulation
2 数值计算结果分析
2.1 计算结果与实验结果对比验证
将非定常数值模拟得到的无倾斜导管桨近壁面,桨后1D截面时均速度场跟Cozijn[17]的PIV试验数据对比,图4结果表明YZ截面时均速度场高度一致,说明了基于Spalart-Allmaras紊流模型的DDES模型进行非定常数值模拟的准确性,可为后续尾流与壁面研究提供精准数据。
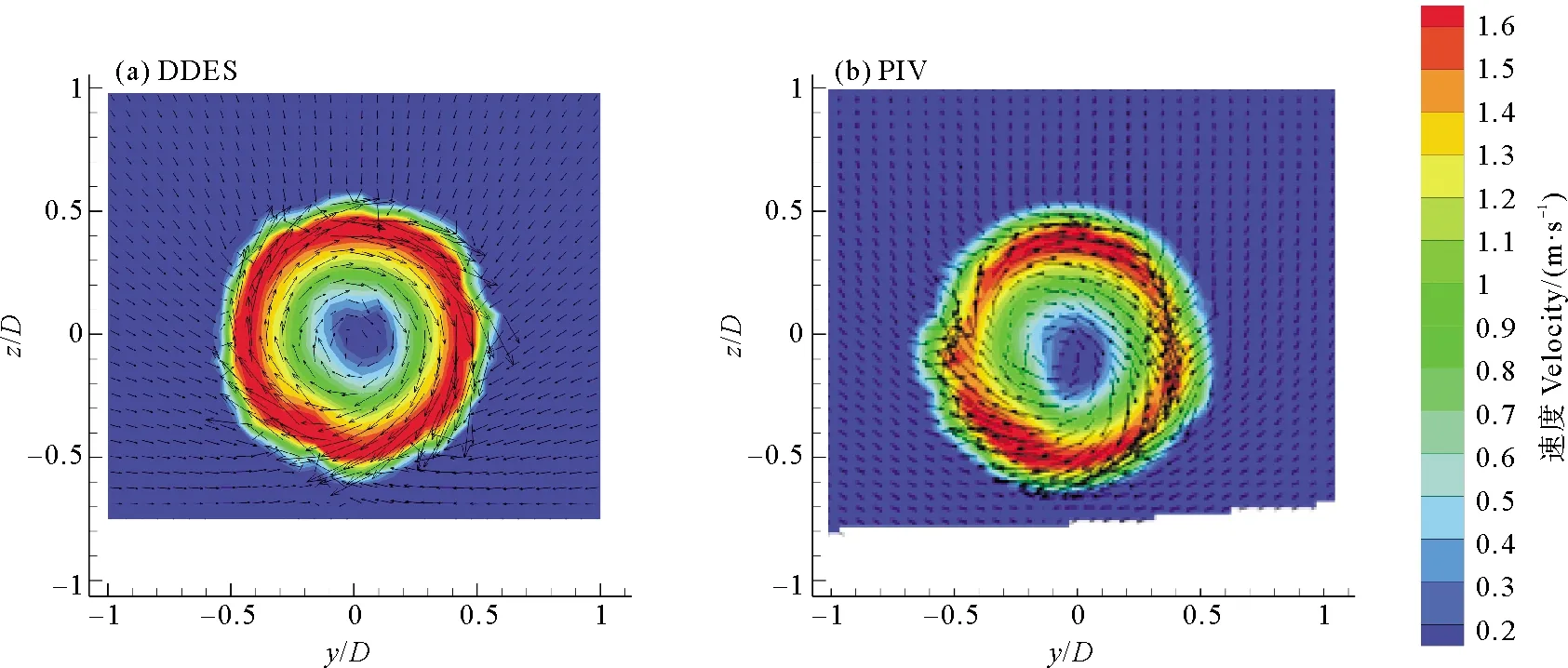
((a)本文数值模拟;(b)文献数值模拟及PIV试验结果[16]。Figure (a) shows the numerical simulation in this paper; Figure (b) shows the numerical simulation and PIV test results[16].)图4 数值模拟及试验结果对比Fig.4 Comparison of numerical simulation and test results
2.2 流场分析
用于导管桨近壁面流场分析的数据不小于10个周期,以尾流场的相位平均结果为主,即10个周期内,每个周期内取四叶桨叶片旋转至同一相位(如0°、90°、180°、270°)的4个瞬时流场的平均值,再取四叶片旋转至相同位置的尾流流场平均值。相位平均流场相较于时间平均流场,能更好的体现平均流场中的流体涡结构;同时,相较于瞬时流场,能更好的过滤掉不重复出现的非主流微小涡结构。
图5显示了导管桨在不同进速和壁面条件下相位平均的速度场变化,图5(a)、(b)是系泊状态下水平和倾斜导管桨,图5(c)、(d)为进速为J=0.4状态下水平和倾斜导管桨。由图5可知,水平壁面对导管桨尾流有明显的吸附作用,即康达效应。对于水平导管桨,这种壁面的吸附作用持续出现在尾流的整个阶段,导致尾流场的不均衡,尤其是系泊条件下更为明显。而对于倾斜导管桨,其尾流场因导管桨的向下倾斜而逐渐偏离导管,但尾流耗散阶段仍然受到壁面的吸引而发生了轻微的转向,有进速情况下,这种转向表现的比系泊状态下轻一些。
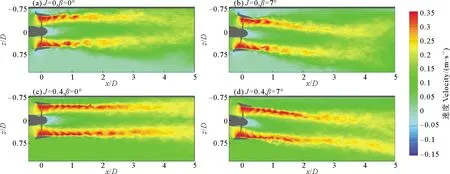
((a)~(d)均以Uref无量纲化。 The flow field in figures (a) to (d) is normalized by Uref.)图5 4个工况下xz平面上沿水流方向无量纲化的相位平均流场Fig.5 Dimensionless phase average flow field along the flow direction on xz plane under four conditions
图6显示并对比了4种状态下近壁面导管桨的相位平均压力场。由图6可知,导管桨尾流压力场最不均衡的是有进速的倾斜导管桨;壁面吸附作用较为明显的还是系泊状态下的水平和倾斜导管桨,尤其是倾斜导管桨的尾流耗散阶段,这与图5的速度场表现一致。对于水平导管桨而言,由于系泊状态下尾流长度比进速状态下短,尾流涡形成的压力环近壁面一侧在导管出口处即受到壁面的作用而被壁面吸附,其后的尾流耗散阶段均受到壁面的影响。有进速的水平导管桨,在环境进速的影响下,很好的维持了原有的压力环,仅在压力环尾部受到壁面影响。对于倾斜导管桨,尾流压力环在系泊和有进速状态下,均表现出不均衡状态,尤其是有进速的情况,原因可能是斜向流与壁面共同作用。

((a)~(d)均以PUref无量纲化。 The pressure in figures (a) to (d) is normalized by PUref.)图6 4个工况下xz平面上沿水流方向无量纲化的相位平均压力场Fig.6 Dimensionless phase average pressure field along the flow direction on xz plane under four conditions
图7显示并对比了4种状态下近壁面导管桨的相位平均动能场。动能场反应的是流体运动的能量,由图7可知,导管桨尾流能量主要集中在螺旋桨旋转和导管形成的叶尖泄露涡环上。壁面对尾涡的影响集中体现在动能较弱的尾涡耗散阶段。值得注意的是,倾斜导管桨的近壁面尾流动能分布依然表现出不均匀性,与压力场分布一致,尤其是有进速的情况。此种现象暗示倾斜导管桨近壁面尾流受斜流的影响可能比壁面的影响要严重。

((a)~(d)均以Uref无量纲化。 The kimetic energy in figures (a) to (d) is normalized by Uref.)图7 4个工况下xz平面上沿水流方向无量纲化的相位平均动能场Fig.7 Dimensionless phase average kinetic energy field along the flow direction on the xz plane under four conditions
图8显示并对比了4种状态下近壁面导管桨的相位平均量级涡度场。由图8可知,与单独导管桨类似,叶尖泄露涡和叶片涡是尾流涡的主要结构,而其受壁面的影响在涡度场中更加清晰可见。涡结构受壁面影响最严重的是系泊状态下的水平导管桨;有进速的水平导管桨尾流虽然保持了大部分的涡结构,但同样在耗散阶段被壁面吸附。对于倾斜导管桨,壁面对系泊状态下的尾流影响较大,而斜流对有进速状态下的尾流影响较大。

((a)~(d)均以Uref/0.5D无量纲化。 The vorticity magnitude in figures (a) to (d) is normalized by Uref/0.5D.)图8 4个工况下xz平面上沿水流方向无量纲化的相位平均量级涡度场Fig.8 Dimensionless phase averaged vorticity field along the flow direction on the xz plane under four conditions
除此之外,在系泊状态下,水平和倾斜导管桨上游导管吸入端,流体由于受到壁面的阻碍和限制,形成了地面涡流(Ground vortex)。此种地面涡一般是在喷气式飞机起飞之前,发动机进气口出现。为了更好的展示地面涡,图9将导管桨近壁面区域放大,可以看出,地面涡在水平导管桨前端的强度要比倾斜导管桨大;而对于有进速的情况,不仅没有出现地面涡,在倾斜导管桨的导管前端甚至出现了涡脱落。
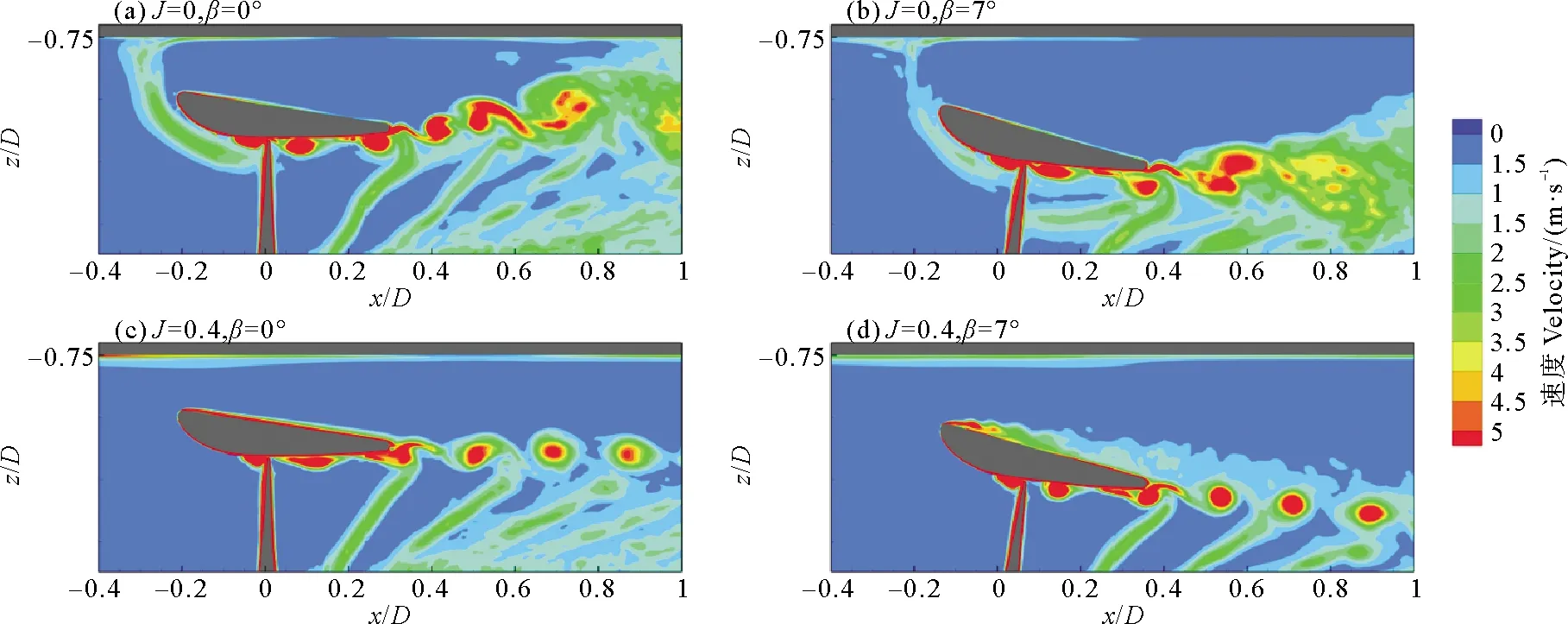
((a)~(d)均以Uref/0.5D无量纲化。 The vorticity magnitude in figures (a) to (d) is normalized by Uref/0.5D.)图9 4个工况下xz平面上沿水流方向,导管桨周围局部放大无量纲化的相位平均量级涡度场Fig.9 Dimensionless phase averaged vorticity field is amplified locally around the ducted propeller along the flow direction on the xz plane under four conditions
为了更好地显示涡量场中主要的涡结构及其消散过程,图10以涡量为基础进行导管桨尾部流场的容积重建,并以涡量大小设置显示渲染透明度,即涡量值越小,透明度越高,从而过滤掉小尺度涡。由图10可知,在系泊状态下,水平导管桨前端近壁面处明显出现地面涡,而后端喷口尾流与壁面吸附;而倾斜导管桨前端不仅有地面涡,还产生了导管前端的漩涡脱落,其尾部流场涡结构仅在耗散阶段被壁面吸引。在有进速的状态下,水平导管桨很好的保持了原有的大部分涡结构,壁面的影响仅体现在耗散阶段,而倾斜导管桨在斜流的主要影响下,相较于水平导管桨,涡结构产生了提前短波失稳的现象。

图10 4个工况下导管桨以无量纲化量级涡度为基础的瞬时尾流场容积重建Fig.10 Volume reconstruction of instantaneous wake field for ducted propeller based on dimensionless vorticity under four conditions
3 结论
本文基于DDES与滑移网格相结合的模型对系泊和进速系数J=0.4工况下的水平导管桨和7°倾斜导管桨进行了数值模拟分析,得出结论如下:
(1)通过对比无倾斜导管桨近壁面的时均速度场与试验结果,验证了基于Spalart-Allmaras紊流模型的DDES模型进行非定常数值模拟的准确性,可以继续进行尾流场及与壁面相互影响的研究。
(2)水平壁面对于导管桨尾流有明显的吸附作用,水平导管桨的近壁面影响持续在整个尾流场所以吸附效果比较明显,相比于系泊状态,水平导管桨在有进速工况下能够较好地维持尾涡形状。而7°倾斜导管桨因为斜流的作用使吸附影响在尾流耗散阶段才表现出来且在斜流与壁面共同作用下使得尾流压力场和动能场表现出不均衡状态。
(3)尾流涡主要由叶尖泄露涡和叶片涡构成,其中受壁面影响最大的依旧是系泊状态下的水平导管桨,因为受进速影响,水平导管桨受壁面的影响作用在尾流耗散阶段比较明显;对于有进速的倾斜导管桨,斜流的影响略大于近壁面的影响。
(4)在涡量分析过程中,发现在系泊状态下,水平和倾斜的导管桨导管吸入端均出现了地面涡流,而在有进速的工况下,倾斜导管桨在斜流的影响下,出现了提前涡结构脱落的现象。
4 展望
对于实际工程应用来说,船舶推进器与港池之间的冲刷和与海洋平台水下动力定位影响机理更为复杂。因此,为了更深入的解决上述问题,可以在本文研究的基础上,进行螺旋桨在近壁面条件下的尾流数值模拟,并将结果和本文结果进行对比,得到不同船舶推进器受壁面影响的差异。另外,可以通过变化导管桨/螺旋桨与壁面间距,得到尾流与壁面间距之间的关系,进一步研究导管桨/螺旋桨与近壁面相互影响的系统性规律。
