弱对角子群与有限群结构

王雪影，申佳昕

（1.广东工业大学 应用数学学院，广东 广州 510520；2.五邑大学 数学与计算科学学院，广东 江门 529020）

本文所讨论的群均为有限群。如果群G 的两个子群H 和K 满足HK=KH，则称子群H 和K 是可换的。1939 年，Ore［1］提出了置换子群的概念：设H 是G 的子群，如果对G 的任意子群K 都有HK=KH，则称子群H 为G 的置换子群。随后，在1962 年，Kegel［2］将置换子群的概念进行推广，提出s-置换子群的概念：如果对群G 的任意Sylow 子群P 都有HP=PH，则称H 为G 的s-置换子群。显然，置换子群一定是s-置换子群，反之不一定成立。

令D（G）=｛（g，g）│g∈G｝，W（G）=｛（g，g-1）│g∈G｝，显然D（G）是G×G 的子群，我们称D（G）为G×G 的对角子群，但是W（G）不一定构成群。例如，令G=Q8=〈a，b│a4=1，a2=b2，ab=a-1〉，则

W（G）=｛（1，1），（a，a-1），（a2，a-2），（a3，a-3），（b，b-1），（ab，（ab）-1），（a2b，（a2b）-1），（a3b，（a3b）-1）｝。取子集W（G）中的元素（a，a-1）和（b，b-1），则会有（a，a-1）（b，b-1）=（ab，a-1b-1），显然（ab，a-1b-1）∉W（G），故此时W（G）不能构成群。对于有限群G，易得到子集W（G）构成群当且仅当G 为交换群。事实上，取G中的任意元素g1，g2，则有（g1，g1-1）（g2，g2-1）=（g1g2，g1-1g2-1）。要使（g1g2，g1-1g2-1）∈W（G）当且仅当g1-1g2-1=g2-1g1-1，即G 为交换群。取G 的任意交换子群M，则W（M）构成群，此时称W（M）为G×G 的一个弱对角子群。

乔守红等［3］研究了对角子群对有限群结构的影响，在此基础上，本文主要研究弱对角子群的一些性质和它的s-置换性，得到了一些有意思的结果。

1 预备知识

引理1［4］设H 是G 的幂零子群，则下列事项等价：

（1）H 在G 中s-置换；

（2）H 的每个Sylow 子群在G 中s-置换；

（3）H 的每个特征子群在G 中s-置换。

引理2［5］设G 为有限群，H 是G 的子群，则H≤F（G）当且仅当H 是幂零群且H 在G 中次正规。

引理3［6］设G 为有限群，H 是G 的Hall 子群，且H◁◁G，则H◁G。

2 弱对角子群的性质

定理1 设G 为有限群，M 为G 的交换子群，对任意的m∈M，则有：

（1）CG（m）×CG（m）=CG×G（〈（m，m-1）〉），特别地，CG×G（W（M））=（CG（M），CG（M））；

（2）NG×G（W（M））=CG（（M），1）·D（NG（M））=（1，CG（M））·D（NG（M））=（CG（M），CG（M））·D（NG（M））。

证明（1）因为CG（m）=CG（m-1），所以有

任取（g1，g2）∈CG×G（〈（m，m-1）〉），则有

即

于是可以得到g1，g2∈CG（m）。因此

综上可得

（2）任取（g1，g2）∈NG×G（W（M）），则可得到g1，g2∈NG（M）。对任意的m∈M，存在m1∈M，使得

也就是

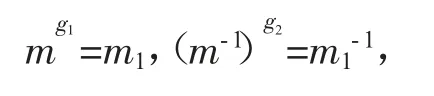
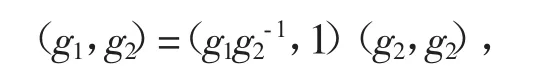
因此可得到

显然

综上可得

对任意的（g3，g4）∈CG（M），g∈NG（M），则有

因此

定理2 设G 为有限群，则：

（1）若H 是C 的子集，W（G）·（1，H）是G×G 的一个子群，则H≤G。特别地，如果H⊆M，则H◁M；

（2）若H1，H2是G 的两个子集，W（G）·（H1，H2）和W（G）·（1，H1H2）是G×G 的两个子群，则

证明（1）任取子集H 中的两个元素h1和h2，则（1，h1），（1，h2）∈（1，H）。由W（G）·（1，H）是G×G 的子群，可知存在g∈G，h∈H，使得

从而有g=1，h1h2=g-1h=h，故h1h2∈H。因此H≤G。

（2）取（1，h1h2）为（1，H1H2）中的任意元素，其中h1∈H1，h2∈H2。则由

可知W（G）·（1，H1H2）≤W（G）·（H1H2）。同理可得W（G）·（H1，H2）≤W（G）·（1，H1H2）。证毕。

定理3 设G 为有限群，H 为G×G 的子群，且W（G）⊆H≤G×G，则存在G 的正规子群K 使得H=W（G）·（K，1）。

证明 首先证明

显然W（G）·（G，1）⊆G×G。因为子集W（G）和子群（G，1）中都有│G│个元素，故只需证明W（G）·（G，1）中的元素表示唯一即可。假设存在G 中的元素w1，w2，g1，g2，使得

即（w2-1w1，w2w1-1）=（g2g1-1，1），故w2w1-1=1，所以有w1=w2且g1=g2。因此G×G=W（G）·（G，1）。同理可得G×G=W（G）·（1，G）。

因为H 是G×G 的子群，故

取H 中的任意元素h，则存在元素g，w∈G 使得h=（w，w-1）（g，1）∈H。又因为（w，w-1）∈H，所以（g，1）∈H∩（G，1），因此

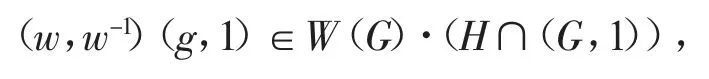
这可推出

显然，W（G）·（H∩（G，1））⊆H。因此H=W（G）（H∩（G，1））。令H∩（G，1）=（K，1），其中K≤G，则H=W（G）·（K，1）。

已知W（G）⊆NG×G（（G，1））且W（G）⊆NG×G（H），所以有

又因为（1，G）中心化（K，1），故

即

从而有（K，1）◁G×G，因此K 是G 的正规子群。证毕。

定理4 设G 为有限群，M 为G 的交换子群，则下列事项等价：

（1）W（M）◁G×G；

（2）M≤Z（G）；

（3）W（M）≤Z（G×G）。

证明 显然，如果M≤Z（G）当且仅当W（M）≤Z（G×G），进一步有W（M）◁G×G。因此，我们只需证：若W（M）◁G×G，则M≤Z（G）即可。

如果W（M）◁G×G，则对任意的g∈G，m∈M，可得到（m，m-1）(1，g)属于子群W（M），所以有m=（（m-1）g）-1，即mg=m。故M≤Z（G）。证毕。

定理5 设G 为有限群，若M 是G 的极大子群且是交换的，则W（M）◁G×G 当且仅当G 为交换群。

证明 若W（M）◁G×G，由定理4 可知M≤Z（G）。因为M 是G 的极大子群，则Z（G）=M 或Z（G）=G。若Z（G）=M，则G/Z（G）=G/M≌Zp。因此G 为交换群，则推出Z（G）=G，矛盾。所以Z（G）=G，此时G 为交换群。证毕。

定理6 设G 为有限群，M 为G 的交换子群，则W（M）◁◁G×G 当且仅当M≤F（G）。

证明 因为M 为交换群，则M×M 为交换群，从而W（M）为幂零群。若W（M）◁◁G×G，则由引理2可知W（M）≤F（G×G）＝F（G）×F（G）。故M≤F（G）。

假设M≤F（G），则M×M≤F（G）×F（G）＝F（G×G）。再一次用引理2 得M×M◁◁G×G，又因为W（M）◁M×M，即W（M）◁◁G×G。

3 弱对角子群的s-置换性

定理7 设G 为有限群，M 为G 的交换子群，且Mp∈Sylp（M）。若W（M）在G×G 中可置换，则：

（1）Op（G）≤CG（Mp）；

（2）M 正规化G 的每个子群。

证明（1）因为W（M）在G×G 中可置换，所以W（M）在G×G 中s-置换。由M 是交换群可得W（M）是幂零群。任取Mp∈Sylp（M），由引理1 可知W（Mp）在G×G 中s-置换。因此，对任意的Q∈Sylq（G）（q≠p），并且我们知道W（Mp）·（Q，Q）是G×G 的一个子群。因为W（Mp）是W（Mp）·（Q，Q）的Hall 子群，且W（Mp）◁◁W（Mp）·（Q，Q），所以由引理3 得W（Mp）◁W（Mp）·（Q，Q）。对任意的m∈Mp，n∈Q，存在m＇∈Mp，使得

即mn=m＇=m，从而有Q 中心化Mp，故可得

（2）设Gp∈Sylp（G），任取x∈Gp，由W（M）在G×G 中置换可知

任取xi∈＜x＞，m∈M，则存在xj∈＜x＞，m1∈M，使得（m，m-1）（1，xi）=（1，xj）（m1，（m1）-1），从而

即有xim=xj，因此M 正规化＜x＞。对任意的g∈G，有因为Mp中心化且Mp正规化＜g＞p，所以Mp正规化＜g＞。由g 的任意性可知，Mp正规化G 的每一个子群。由Mp的任意性且M 可由它的所有Sylow 子群生成知M 正规化G 的每个子群。证毕。

反之，若M 正规化G 的每个子群，我们不能推出W（M）的置换性，但对任意的H1，H2≤G，可得D（M）和W（M）置换H1×H2。并且由上述定理的证明过程可知，若条件减弱为W（Mp）在G×G 中s-置换，此时依然能够得到Op（G）≤CG（Mp），并且这还是一个充要条件，于是有了下述定理。

定理8 设G 为有限群，M 是G 的交换子群，且Mp∈Sylp（M），则下列事项等价：

（1）W（M）在G×G 中s-置换；

（2）W（Mp）在G×G 中s-置换；

（3）Op（G）≤CG（Mp）。

证明 由M 是交换群可知W（M）是幂零群。通过引理1 可知W（M）在G×G 中s-置换当且仅当W（Mp）在G×G 中s-置换。根据定理7 的证明过程可知Op（G）≤CG（Mp）。因此我们只需证明：若Op（G）≤CG（Mp），则W（Mp）在G×G 中s-置换。

因为Mp◁Op（G）Mp◁◁G，故Mp◁◁G。又因为Mp是幂零群，所以Mp≤F（G），进而有Mp≤Op（G）。因此，Mp包含在G 的每个Sylow p-子群中。故对任意的P∈Sylp（G×G），有

又因为Op（G）≤CG（Mp），因此W（Mp）在G×G 中s-置换。