Banach 空间中的凸区域和一致域

管甜甜，欧阳正勇

（佛山科学技术学院数学与大数据学院，广东佛山 528000）

John［1］在研究局部单射的整体性态时引入了一类域，即一致域。Martio［2］和Gehring 等［3］深入研究了欧氏空间中的一致域，Martio 给出了一致域的等价刻画。Zhou 等［4］讨论了无限维实Banach 空间中一致域的一些性质以及一致域在拟Mobius 映射下的不变性。Vaisala［5］在研究无限维实Banach 空间中的拟共形映射理论时，讨论了Banach 空间中一致域的相关性质，同时，Vaisala 研究了Banach 空间中某些特殊区域的一致性。例如，球、球去掉球心以及整个Banach 空间去掉一点之后的区域都是一致域，所得结果具体如下。

引理1［5］假设E 是维数大于或等于2 的实Banach 空间，x0∈E，r＞0。那么B（x0，r），B（x0，r）｛x0｝和E｛x0｝是v-一致域，其中v 是一个常数。

Vaisala 还得到了一致域除去一点之后的区域仍是一致域。

引理2［5］假设E 是维数大于或等于2 的实Banach 空间，G⊂E 是v-一致域和x0∈G。那么G｛x0｝是v1-一致域，其中v1依赖于v。

Vaisala［6］证明了有界凸区域是一致域，所得结论如下：

引理3 假设E 是维数大于或等于2 的实Banach 空间，G⊂E 是一个凸区域且存在x0∈G 和R2＞R1＞0 使得B（x0，R1）⊂G⊂B（x0，R2）。那么G 是v-一致域，其中v 依赖于R2/R1。

我们知道Minkowski 泛函和凸区域有紧密的联系［7-8］，本文使用Minkowski 泛函进一步讨论凸区域的一致性，所得结论如下。

定理1 假设E 是维数大于或等于2 的实Banach 空间，C⊂E 是一个关于x0∈C 对称的凸区域，且存在R2＞R1＞0 使得B（x0，R1）⊂C⊂B（x0，R2）。则有：

（1）C 是v1-一致域；

（3）C｛x0｝是v3-一致域。

其中，v1，v2和v3都只依赖于R1和R2。

注 定理1 的证明方法与引理2、引理3 的证明方法完全不同，定理1 的证明结合了Minkowski 泛函，而引理2 和引理3 则由一致域的定义直接证明，定理1 的证明给凸区域一致性的研究提供了新的思路和方法。

1 预备知识

首先介绍Banach 空间的相关术语，详见参考文献［5］。设E 表示维数大于或等于2 的实Banach 空间，表示E 中的范数。A⊂E 是一个集合和∂A 分别表示它的闭包和边界。一个有界集合A⊂E 的直径记为diam（A）。以x 为中心，半径为r＞0 的开（闭）球记为

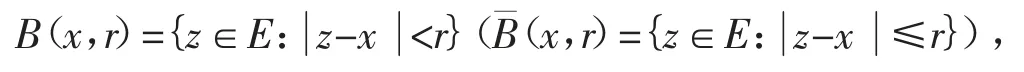
球面记为

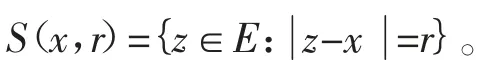
定义1 设A⊂E 是一个集合。如果它有如下几何性质：当x∈A，y∈A，且0＜t＜1 时，有zt∈A，其中

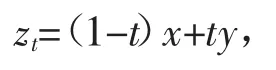
则称它是凸集。特别地，如果A 还是一个区域，即连通的开集，称它是凸区域。

Banach 空间中的开（或闭）单位球都是凸的。

定义2 假设C⊂E 是一个凸集且包含x0。我们称C 是关于x0对称的，如果对x0+x∈C 均有x0-x∈C。

定义3 假设v≥1 是一个常数。若对于区域G 中的任意两点x 和y，都存在一条曲线γ 连接它们并满足下列性质：

（1）对所有的z∈γ，min｛l（γ［x，z］，l（γ［z，y］）｝≤vd（z）；

则称G 是v-一致域，其中，γ［x，z］表示曲线γ 介于x 和z 之间的部分，l（γ［x，z］表示γ［x，z］的曲线长度，d（z）表示点z到G 的边界∂G 的距离。

2 定理1 的证明

在证明定理1 之前，我们先证明如下引理。

引理4 假设C⊂E 是一个关于o 对称的有界凸区域，且存在实数R2＞R1＞0 使得B（o，R1）⊂C⊂B（o，R2），其中o 为E 中的零元。对x∈E，令

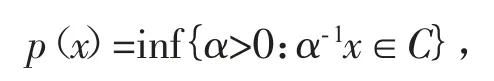
称函数p（x）为关于C 的Minkowski 泛函，简记为p。则（E，p）是一个Banach 空间且对x∈E 满足

进一步有，C=｛x∈E：p（x）＜1｝。

证明 假设C⊂E 是一个关于o 对称的有界凸区域。因为存在实数R2＞R1＞0 使得B（o，R1）⊂C⊂B（o，R2），所以对任意的x∈E 有

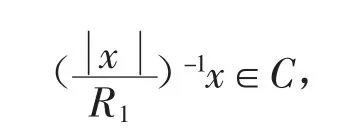
由假设可知，存在实数R2＞R1＞0 使得B（o，R1）⊂C⊂B（o，R2），所以对任意的x∈E 有

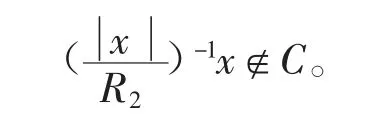
接下来，证明（E，p）是一个赋范线性空间。由文献［9］中的命题1.5.6 和1.5.8，我们只需要证明p（x）=0 可得x=o 即可。因为p（x）=0，所以存在αn＞0 满足当n 趋于0 时，αn趋于0 并且使得

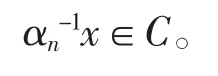
又因为C 是有界的，于是x=o。

最后，（E，p）的完备性由E 是一个完备的赋范线性空间和式（1）可得。

定理1 的证明 假设C⊂E 是一个关于x0对称的有界凸区域，其中x0∈C。关于C 的Minkowski 泛函为p。由于凸性、一致性和有界性是关于平移变换不变的，不失一般性假设x0=o。

同样地，由引理4 可知，（E，p）为Banach 空间和C 是（E，p）中以o 为球心的单位球。因此，C 在（E，p）中是c1-一致域，其中c1是一个常数，和是（E，p）中单位球的补集。

假设up是（E，p）中关于以o 为球心的单位球面的反演变换。则由文献［10］可知且up是θ-拟Mobius 映射，其中控制函数θ（t）=81t。又由文献［5］中的定理6.26，一致域关于拟Mobius 映射是不变的，所以在（E，p）中是c2-一致域，其中c2是仅依赖于c1的常数。再由引理4 可知，范数p 和范数等价，其中参数依赖于R2/R1。从而C 在这两个范数诱导的度量双Lipschitz 等价。又因为一致域是双Lipschitz 不变的，所以是c3一致域，其中c3只依赖于R2/R1。定理1 得证。