基于Excel的直线拟合问题不确定度评定研究
2022-06-02赵云飞邱成锋贾小文张金凤范海英
赵云飞,邱成锋,贾小文,张金凤,范海英
(陆军军事交通学院 基础部,天津 300161)
大学物理实验经常会遇到直线拟合问题,逐差法和最小二乘法是解决这一问题的常用方法。这两种方法的优劣是大学物理实验争论已久的问题。而Excel又是一款常用的软件,是学生通过全国计算机等级一级考试时的必考内容。本文以Excel 2016为计算工具,分别用逐差法和最小二乘法处理“拉伸法测金属丝的杨氏模量”实验数据,通过评定测量结果的不确定度对这两种数据处理方法分析比较。
1 金属丝杨氏模量的测量
1.1 实验原理
一根长为L,截面积为S的均匀金属丝,在沿长度方向外力F的作用下,其伸长为δl,设金属丝的直径为d,则金属丝杨氏模量E为:
(1)
式(1)中,F、L、d比较容易测量,微小变化量δl测量困难。下面利用CCD成像系统来测量δl。如图1所示,在悬垂的金属丝下端连着十字叉丝和砝码盘,当盘中加上质量M的砝码时,金属丝受力增加了F=Mg,g为当地的重力加速度,例如天津地区约为9.801 m/s2。十字叉丝随着金属丝的伸长下降。叉丝板通过显微镜的物镜成像在最小分度为0.05 mm的分划板上后被目镜放大,通过监视器观察,从而实现对δl进行测量[1]。
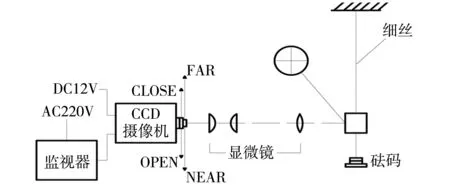
图1 测量原理图
1.2 数据测量


表1 金属丝直径的测量


表2 金属丝伸缩变化测量

图2 砝码质量与伸缩变化量关系图
2 直接测量量的标准不确定度评定
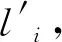

表3 直接测量量标准不确定度
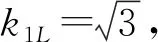

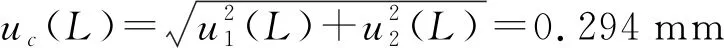
金属丝直径d共测量6次,以平均值作为最佳估计值,需考虑测量重复性带来的标准不确定度分量u2(d),用函数“=STDEVA(B11:G11)/SQRT(6)”计算,结果为:u2(d)=0.000 577 mm。
因此测量量d的合成标准不确定度为:
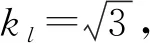

因此测量量l的合成标准不确定度为:
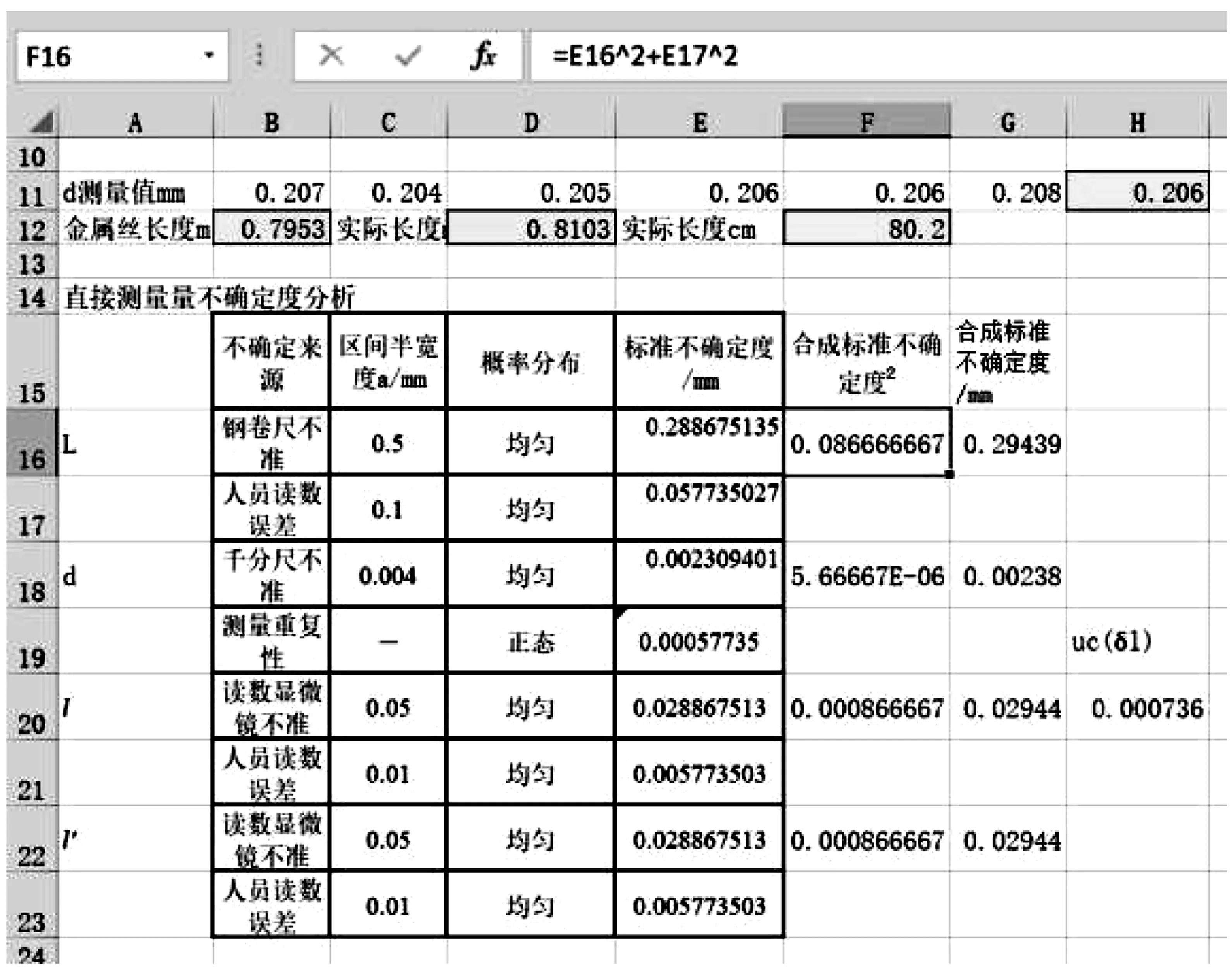
图3 Excel数据处理示例
3 求解金属丝的杨氏模量并评定δl的标准不确定度
3.1 利用逐差法求解

(2)
利用式(1)并编写Excel计算公式“=4*9.801*F12*10^4/(PI()*H11^2*E4)”可得金属丝的杨氏模量E(公式中的E4为(2)式的计算结果):
(3)
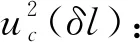
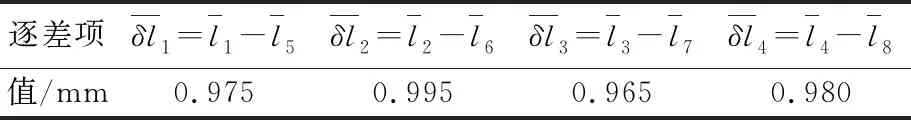
表4 逐差法求解伸缩变化测量
由表4可知
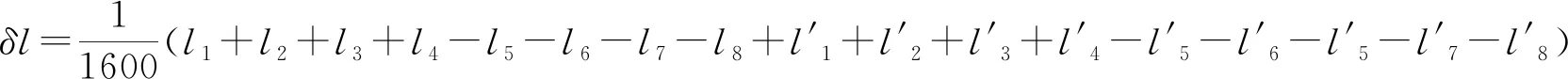
所以利用不确定度传播律,可得:
(3)
(4)
3.2 利用最小二乘法求解


图4 “linest”函数使用示例
利用“linest”函数求得斜率k=-0.001 229 46,再利用函数“=ABS(I16)”取绝对值,即可计算出每增加1 g质量金属丝的伸长量δl=0.001 229 mm。δl的实验标准偏差也可利用函数“linest”求解出来,计算结果参见图4Excel表“I17”。
uc(δl)=s(δl)=6.97×10-6mm
(5)
由此可以计算出金属丝的杨氏模量为:
(6)
4 结 语
4.1 评定用逐差法求伸长量后E的不确定度
由不确定度传播律可得:
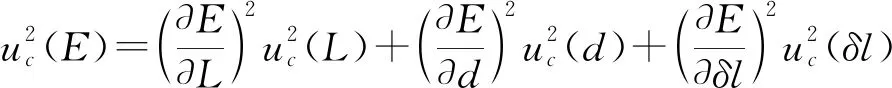
(7)
代入数据并Excel软件编写公式可以计算得出(g=9.801 m/s2):
=-187 154 995 g·m·cm/(s2·mm4)
=-15756394983 g·m·cm/(s2·mm4)
将uc(L)、uc(d)和uc(δl)的值分别代入后,可得:
=1.16×1011Pa
取包含因子k=2,则被测金属丝杨氏模量E的扩展不确定度:
U=2uc=2.4×1011Pa
(8)
因此,E=(1.9±2.4)Pa,用逐差法求解δl后E的扩展不确定度太大,明显不合理。
4.2 评定用最小二乘法求伸长量后E的不确定度
同理,可求出利用最小二乘法求解δl后
=-186237568.6 g·m·cm/(s2·mm4)
=-15602299137 g·m·cm/(s2·mm4)
将uc(L)、uc(d)和uc(δl)的值分别代入,可得
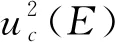
=0.046×1011Pa
取包含因子k=2,则被测金属丝杨氏模量的扩展不确定度:
U=2Uc=0.09×1011Pa
因此,E=(1.92±0.09)Pa,比较而言,实验中用最小二乘法求解δl更加合理,逐差法只适合计算条件不方便时估算测量结果。
