待测板温度场分布对导热系数测量的影响

于莉莉，郭 远，裴 能，喻 孜

(南京林业大学 理学院，江苏 南京 210037)

材料导热系数的测定是工程热物理、材料科学及能源、环保等各个研究领域的重要课题[1-3]。实验测量固体导热系数的方法一般分为稳态法和瞬态法。在稳态法中，先利用热源对样品加热，通过控制实验条件，使加热和传热过程达到平衡状态，通过测量同等条件下散热盘的散热率计算出样品的导热系数。

在测量散热盘散热率时通常有两种处理方法，一种是使升温后的散热盘单独散热，基于散热率与面积成正比，对散热面积进行修正计算导热系数。然而由于实验过程中风扇的鼓风，各个面的热流密度存在较大差异，直接假定各个面的冷却速率相同进行面积修正有一定的误差[4]。另一种方法是覆盖样品盘到散热盘，还原稳态时的情景，通过计算散热盘稳态温度时的散热率得到导热系数。然而，待测板覆盖前已在空气中冷却了一段时间，其内部温度梯度的变化会影响到散热盘的散热情况，导致导热系数测量误差，但是这方面的研究甚少。本文将通过数值模拟，研究待测板内部温度变化对散热盘散热率及导热系数结果的影响，为实验设计提供参考。

1 实验简介

实验使用杭州大华YBF-2型仪器。装置如图1所示。上下盘分别是加热铜盘和散热铜盘，中间是待测样品盘。给上铜盘加热，热量就由高温铜盘传递给待测盘，再由待测盘传递给低温铜盘。

图1 实验室测量导热系数示意图

用T1和T2分别表示待测板上下表面温度，R是圆盘半径，h是厚度，λ表示待测板的导热系数。则单位时间内由高温区向低温区传导的热量，即传热率：

(1)

待测板的传热率是一个无法直接测量的量，可将其转化为较为容易测量的量。

当热传导达到稳态时，T1和T2的值不随时间变化，此时待测盘内有稳定的温度梯度，单位时间通过待测盘的传热率与散热铜盘的散热率相同。散热铜盘在稳态温度的散热率为：

(2)

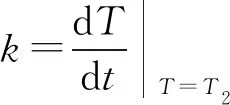
为了得到斜率k，在系统达到稳定状态后，移去待测板，让加热板继续对散热板加热，待散热盘温度比稳定温度T2高10 ℃左右时，移去加热板，覆盖待测板到散热盘上，还原稳态时的情景，记录散热盘的温度随时间的变化，得到稳态温度T2时的斜率k，联立(1)和(2)得到待测板的导热系数：

(3)

2 数值模拟计算与讨论

2.1 稳态温度场

采用COMSOL建立二维轴对称模型，首先模拟系统达到稳态时的温度场分布。盘的半径R和厚度h分别为R=6.5 cm，h=8.0 mm，环境温度为20 ℃。用U(T)表示温度分布函数，稳态固体散热方程为：

λΔU(T)=0

(4)

实验采用手动加热方式，系统最终的稳态电压：V1=4.91 mV，V2=2.74 mV，根据铜-康铜热电偶分度表，该电压对应T1=113 ℃，T2=66 ℃。另外实验过程中要打开仪器风扇加快稳定过程，因此模拟时设置加热板为恒温113 ℃，系统侧面及散热板下表面采用强制条件，换热系数αt=15 W/m2·℃[5,6]，样品盘导热系数λ=0.162 W/(m·℃)[1]，散热铜盘的质量m=845.0 g。稳态后的温度分布如图2所示，计算结果显示待测板上表面的稳定温度为113 ℃，下表面的稳定温度为66 ℃，与实验数据完全符合。

图2 系统稳态温度分布

待测板的内部有稳定的温度梯度，图1上的箭头表示热流方向，在待测板内部热量由上至下传输，但由于侧面散热的原因，在板的边缘热量传输的方向发生改变。

2.2 待测板自然冷却

系统达到稳定状态后，移去待测板，使加热板继续加热散热板，此时的待测板在空气中自然冷却降温，内部原有的稳定温度梯度发生改变，这里我们采用瞬态法模拟待测板的降温过程，边界条件采用自然对流，换热系数[5,6]。待测板不同时刻的温度分布如图3所示，由于边界散热，热量向周围的空气传递，随着时间的流逝，温度场趋向中心对称分布。

(a)初始时刻

(b)5 min

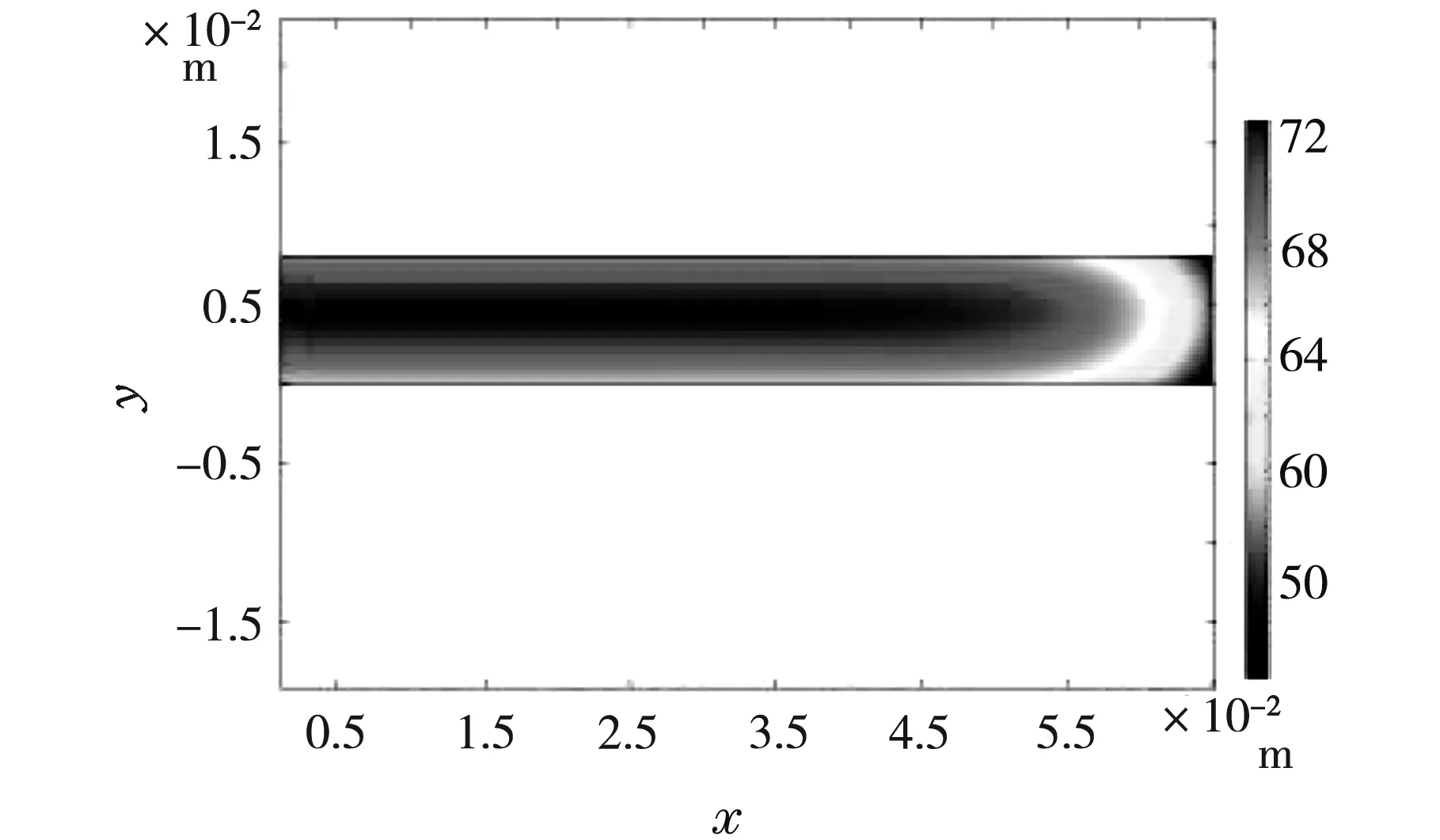
(c)10 min

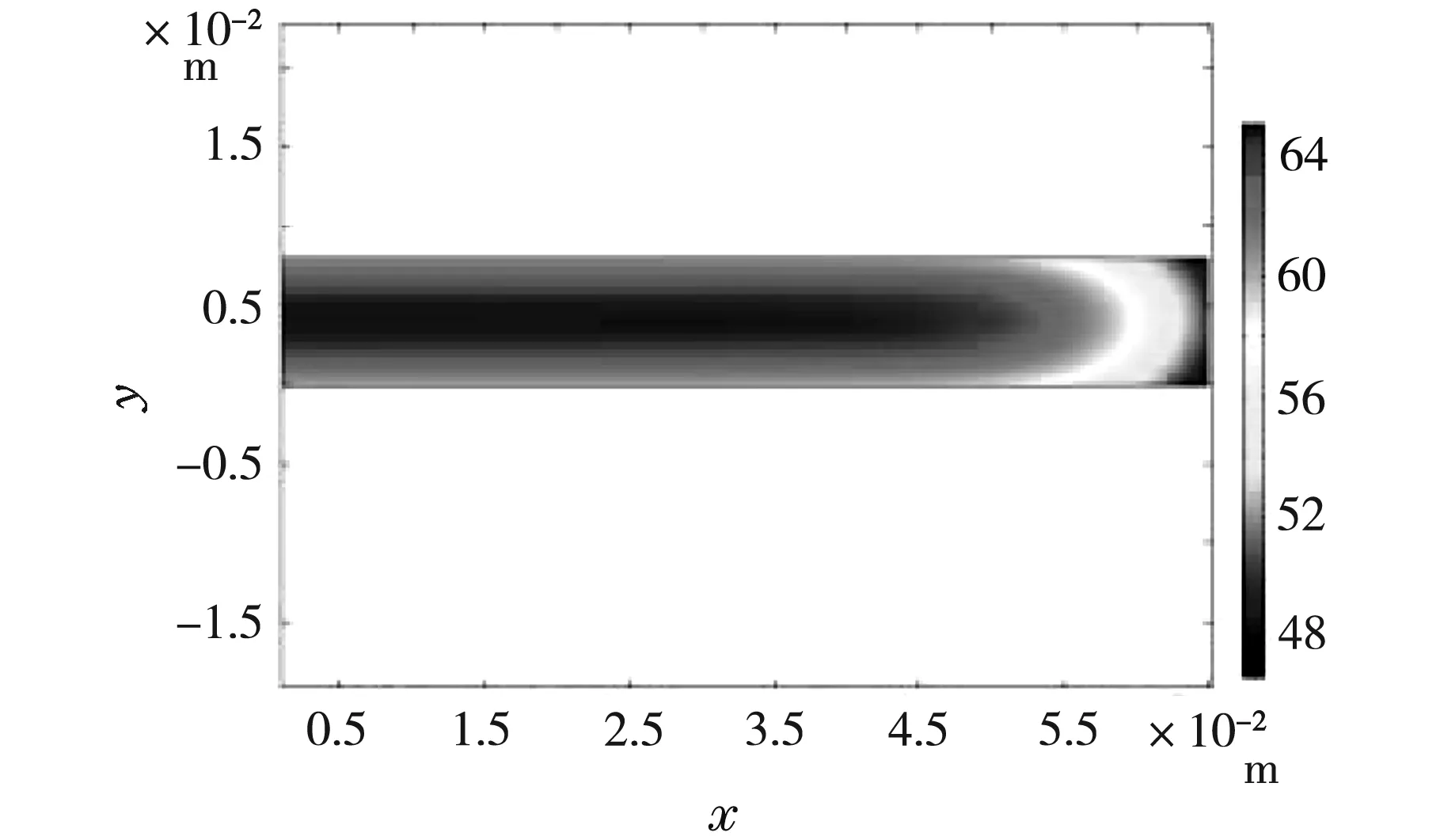
(d)15 min图3 待测板不同时刻的温度分布

2.3 待测板和散热盘降温过程

将加热板与散热板直接接触加热，当散热板的温度比稳态T2升高10 ℃时，移走加热板，覆盖待测板于散热盘上。考虑到散热铜盘在加热的过程中，待测板也同时暴露在空气中自然冷却。因铜盘受实验装置和操作方法影响，加热结束的时间不确定，覆盖于铜盘上的待测板在对应时刻的冷却状态也不同，将待测板不同时刻自然冷却的状态设为二板系统的初始状态。图4是待测板和散热铜盘初始状态，此时待测板的温度分布对应其在空气中单独自然冷却15 min时的温度分布，铜盘的温度为76 ℃。从图上可以看出，此时待测板的温度内热外冷。用瞬态法计算系统散热过程，每隔10 s记录铜盘中心温度，拟合铜盘降温曲线并利用excel的Trend函数[7]得到稳定点66 ℃时的斜率k=-0.034 6 ℃/s，代入式(3)得到待测板的导热系λ=0.143 W/(m·℃)，小于理想的导热系数λ=0.162 W/(m·℃)。

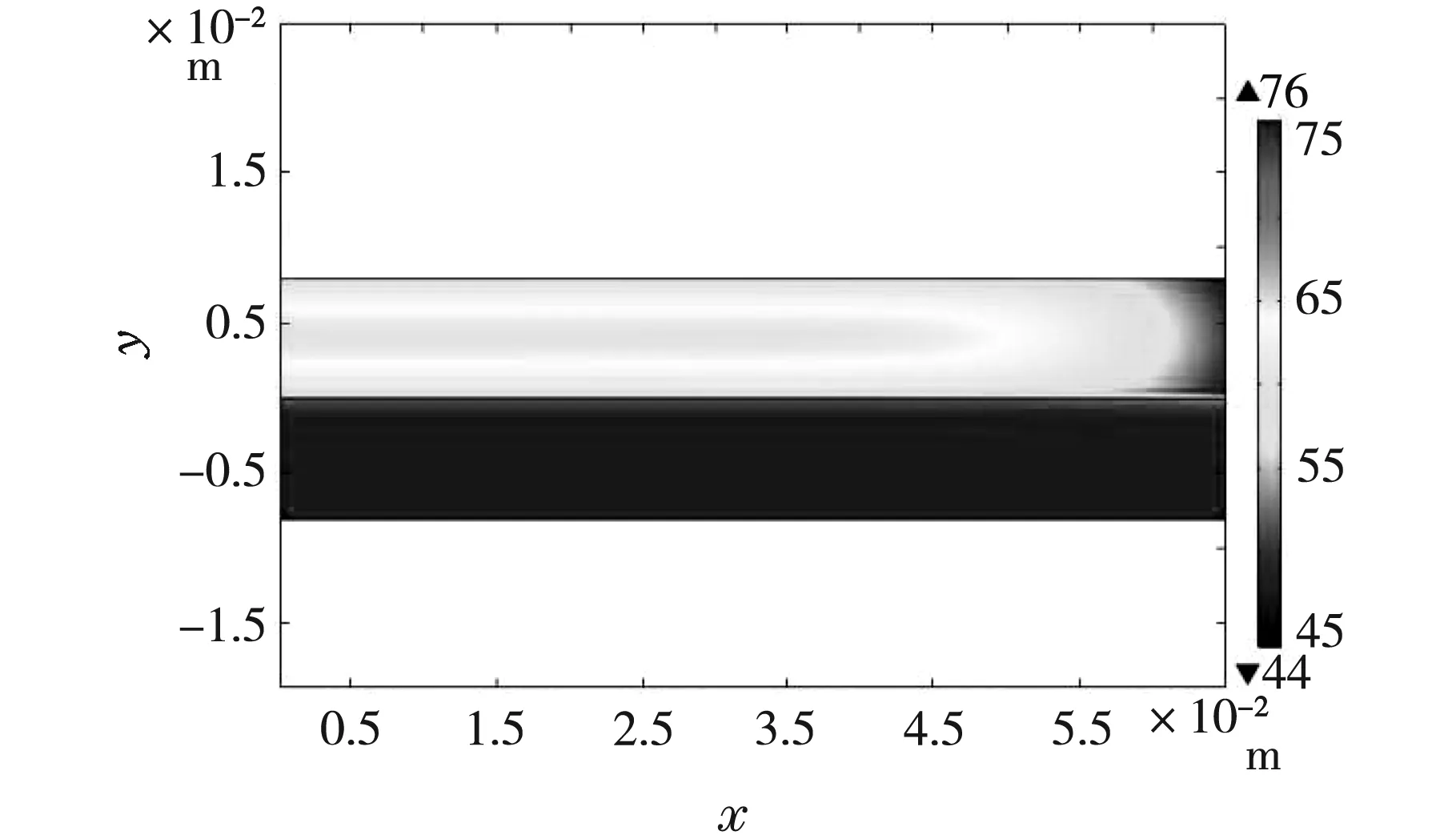
图4 待测板(自然冷却15 分钟时)置于铜盘初始时刻的温度分布

待测板的初始状态不同，铜盘和待测板接触面之间的温度梯度也会有差异。如图4所示，两板接触面间的大致初始温差为16 ℃。增加温差，将会增加散热率。现将待测板自然冷却15～20 min的初始状态分别代入模型计算，得到铜盘降温过程稳定温度66 ℃的斜率k和待测板导热系数λ，如表1所示：

表1 待测板冷却时间与铜盘散热斜率和待测板导热系数的关系

从图5可以看出导热系数与待测板的冷却时间成正比关系λ=0.008 4t+0.017 5(t单位为分钟)，根据图中的线性关系式，可知待测板冷却到17.2 min时对应的λ=0.162 W/(m·℃)，根据预测将待测板17.2 min时刻的自然冷却状态作为系统的初始状态，代入模型计算，得到铜盘的降温数据，如表2所示。

图5 待测板自然冷却时间与λ关系图

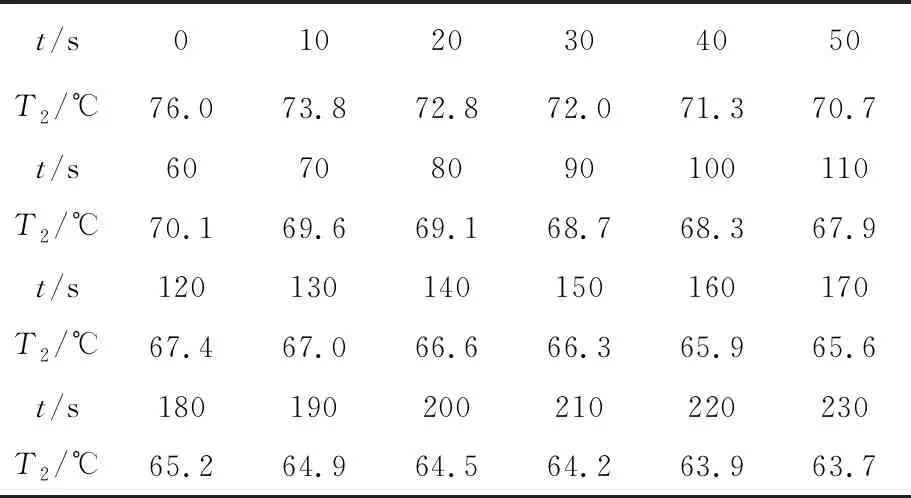
表2 散热铜盘温度T2与时间t的关系

利用excel的Trend函数得到散热铜盘降温到66 ℃时的时间为154 s，此时系统的温度场分布如图6所示，其中面上的箭头表征热流的大小和方向。与三板系统稳态时(图2)对比，热流的方向从铜盘流向了待测板及边界。待测板的上下面(～52 ℃和66 ℃)温差大致为14 ℃。

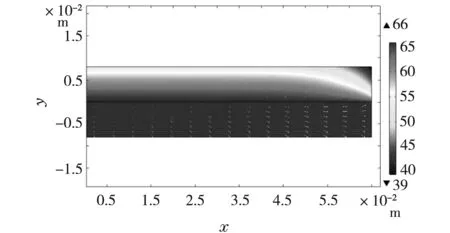
图6 系统在散热板66 ℃时的温度分布

如果待测板的温度为稳定点66 ℃恒温，散热铜盘由于初态温度比待测板高，热量由铜盘向待测板和周围空气传递，但待测板的不良导热性和较小的温差使铜盘散热率较小，其降温曲线在稳定点的斜率k=-0.030 8 ℃/s，对应得到待测板的导热系数为λ=0.127 W/(m·℃)，相对误差为21.6%。在条件不变的情况下，计算待测板45～65 ℃恒温时，散热铜盘稳定点的斜率及对应的导热系数，结果如表3所示：

表3 待测板恒温情况下铜盘散热斜率和待测板导热系数的关系

这里导热系数λ与待测板温度不是简单的线性关系，在55～60 ℃区间每隔1 ℃计算可知，待测板58 ℃得到理想的导热系数。

3 结 语

物理实验中常使用稳态法测量不良导体的导热系数，考虑到面积修正法中散热盘各表面散热率不相等的问题，常采用覆盖待测板在散热盘上，还原稳态场景的方式测量导热系数，但误差仍然存在，本文模拟该实验过程，并分析误差原因。

模拟计算的三个过程包括：稳态加热，待测板抽离自然冷却，待测板和散热盘降温过程，根据实验情况，相应的考虑了强制对流和自然对流条件，待测板被抽离后的自然冷却过程中，内部温度场随时间而变化，研究表明待测板置于散热盘上的降温过程中，待测板初始的内部温度分布影响导热系数的大小，待测板在空气中的冷却时间与导热系数成一次线性关系，20 ℃室温的情况下，理论导热系数λ=0.162 W/(m·℃)对应待测板冷却时间为17.2 min，过早(过晚)会导致导热系数偏小(偏大)；若待测板保持恒温58 ℃，可得到理想的导热系数。

散热铜盘的散热率不仅与自身物理属性，环境温度有关，还与接触物的传热属性和温度分布有关。在相同条件下，待测板内部温度场的不同，将得到不同的导热系数，这是导致该方法测量误差的主要原因。实验上若采用散热盘单独降温的面积修正法，应该考虑到各面热流密度不同，需将此差异纳入面积修正中[4]，并进行温度补偿[8]。