微波超视距雷达组网探测范围研究

汤华涛 察豪 田斌 王彬彬

（海军工程大学电子工程学院，武汉 430033）

引 言

微波超视距雷达是一种常用的对海探测雷达，在蒸发波导条件下，该雷达可实现超视距探测，即对舰船目标的探测距离大于视距. 为了评估微波超视距雷达的探测效能，以提供准确的信息保障服务，必须根据波导条件实时估计其对舰船目标的探测范围.然而，超视距探测时雷达对舰船目标探测距离的估计不同于视距，传统的雷达方程已不再适用，需考虑蒸发波导条件下传播因子的变化情况[1]. 同时，随着雷达装备的发展，构建以网络中心为主的雷达组网已成为必然趋势，通过雷达组网，可以在不改变现有装备性能的前提下，经过不同的组织形式来提高雷达的远距离探测、反隐身和抗干扰能力[2]. 因此，研究微波超视距雷达组网状态下对舰船目标的探测范围具有重要的军事意义.

微波超视距雷达探测目标时电磁波不再是直线传播，在目标处不同高度上的入射波传播因子不同，即目标处入射波的强度与高度有关. 在考虑传播因子的基础上，文献[3-4]通过求解电磁波传播的抛物方程，得到了蒸发波导条件下雷达作用距离的一种估计方法. 文献[5-8]也做了类似的工作. 但是，以上研究没有考虑目标雷达散射截面(radar cross section,RCS)在方位角上的起伏，都假设目标RCS 周向均匀分布，且研究对象为单部雷达.

通常情况下，舰船目标RCS 随方位角的变化起伏很大，不考虑目标RCS 起伏得到的探测距离估计会与实际探测距离有所差异；同时，当雷达组网时，不同雷达对目标的观测角度不同，得到的探测距离估计也不相同，多部雷达互补后得到的探测距离估计也将不同于单部雷达. 本文在蒸发波导传播特性研究的基础上，同时考虑舰船目标RCS 在高度和方位角上的分布，建立雷达组网时对舰船目标的探测范围评估模型，分析雷达组网对舰船目标探测范围的影响.

1 蒸发波导传播因子估计

式中：F 和F-1分别表示傅里叶变换及傅里叶反变换因子；p=ksina，a为传输角.

2 舰船目标最大探测距离计算

任何目标的RCS 值都会随探测方位角的不同而产生剧烈的变化[2]. 为了得到舰船目标RCS 随方位角的变化情况，可利用仿真软件建立舰船的三维几何模型，然后计算其周向RCS，也可以通过实验测试得到舰船目标不同角度RCS 值σθ，观测方位角为θ.而对于目标RCS 在高度上的分布，与其相关的研究较少，目前还没有成熟的理论成果[9-10]. 根据参考文献[11]，可假设舰船目标RCS 在垂直高度上的分布服从高斯分布，且其分布密度函数为p(z)，设目标高度为h，将目标在高度上划分为N等份，若N取值较大，每等份可近似作为点目标处理，则可得到高度为nΔz(n=0,1,2,···,N-1)的部分RCS 为

式中：Pr和Pt的单位均为dBW；G、Ls、L(R)的单位为dB；λ 的单位为m；σθ的单位为m2.

设雷达接收机灵敏度为Stmin，当Pr=Stmin时，可计算得到Rθ=Rmax，即得到观测方位角为θ 时雷达对舰船目标的最大探测距离Rθ.

3 雷达网探测范围评估模型

设有M部雷达组成雷达网，雷达网中有一部雷达探测到目标即视为雷达网探测到目标. 以某部雷达为坐标原点，建立直角坐标系，如图1 所示，则其他雷达的坐标为 (xi,yi)(i=2,3,4,···,M). 假设与x轴夹角为 φ的方向上有一个目标，且轴线与正北方向夹角为φ，目标到原点的距离为d，则雷达网评估模型详细步骤如下：

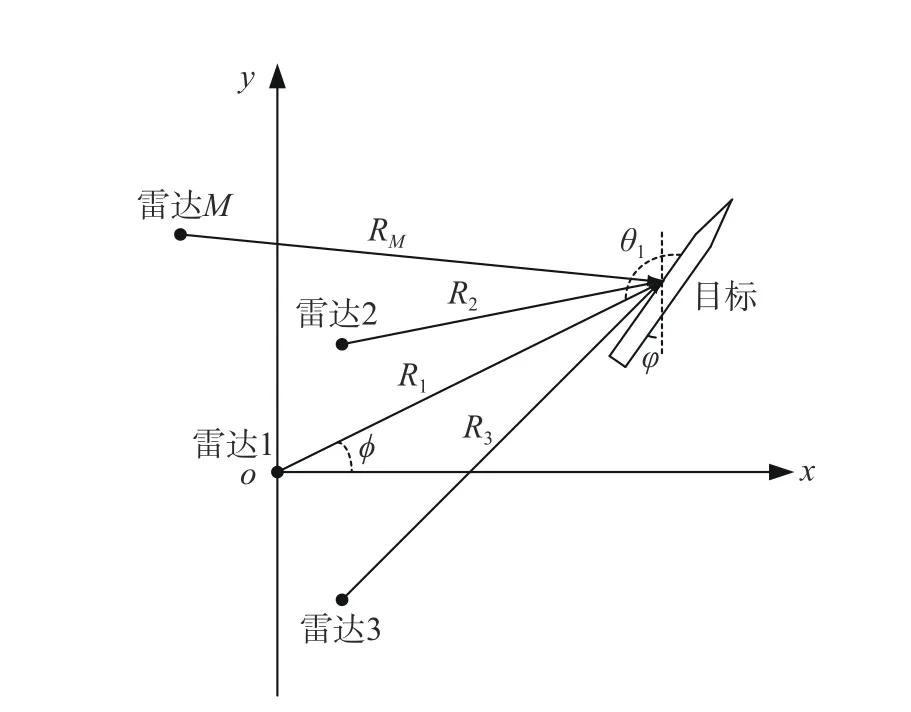
图1 雷达组网探测示意图Fig. 1 Diagram of detection radar network

1)计算雷达网各雷达对目标的观测距离和观测角：

上述评估模型同时考虑了蒸发波导和雷达组网对目标探测距离的影响，将目标RCS 按高度和方位角分布描述，并将雷达网对目标的全周向最大探测叠加，最终得到了雷达网对目标的探测范围. 值得注意的是，本文在计算雷达网 φ方向上的目标最大探测距离时，采用的判定条件是目标自身姿态角φ 在0～359°的任何角度上(分辨率为1°)，雷达网都能探测到目标，与传统的最大探测距离计算方法有所不同.

4 仿真分析

以某舰船为研究对象，其RCS 随方位角起伏较大，在左右舷约90°及舰尾方向存在极大值，对目标总体RCS 贡献较大，RCS 最大值为1.12×106m2，平均值为5.4×104m2. 蒸发波导高度12 m.

设由三部岸基微波超视距雷达组成雷达网，从南到北依次布设，坐标分别为雷达1(0，0)、雷达2(5，10)、雷达3(5，-10)(单位为km)，监视东面海域舰船目标，雷达1 所在的y轴为海岸线. 三部雷达参数相同，设置检测概率90%、虚警概率10-6.

4.1 假设舰船目标的航行姿态未知

此时目标的轴线与正北方向夹角未知，认为雷达对目标的观测角可能为任意角度，利用文献[2]中的方法单独计算各雷达对目标的最大探测距离为79 km，并将探测范围相互叠加，与本文中雷达组网时的方法计算结果做对比，结果如图2 所示.

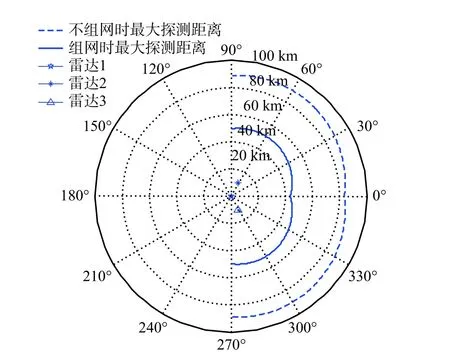
图2 目标航行姿态未知时的有效探测范围Fig. 2 Effective maximum detection range of unknown navigation attitude

图2 中，雷达不组网时，各雷达探测范围相互叠加后最大探测距离大约为90 km；雷达组网时的探测范围反而比不组网时小，最大探测距离约为50 km.但事实上，文献[2]中在计算各雷达对目标的最大探测距离时，采用的是目标平均RCS，由于目标RCS 在方位角上的起伏特性，目标各方位角上RCS 大于平均RCS 的占比为19%，即用文献[2]中的方法计算得到的结果准确率为19%，当目标的航行姿态未知时，雷达对目标的最大探测距离有81%的概率达不到90 km. 而本文算法得到的最大探测距离为最大有效探测距离，即目标的航行姿态未知时，雷达网对目标的最大探测距离至少为50 km. 为了研究雷达组网对目标最大探测距离的影响，使用本文第3 节建立的雷达网评估模型时，在第2 步、3 步中，若全部Pri＜Stmin，并不立即进入第4 步，而是继续以1°的步长增加φ 直至φ+359°；若在φ+1°～φ+359°的所有角度上，存在Pri=Stmin的占比大于等于19%，则进入第5步，否则进入第4 步. 使用更改后的雷达网评估模型计算准确率为19%时的最大探测距离如图3所示.

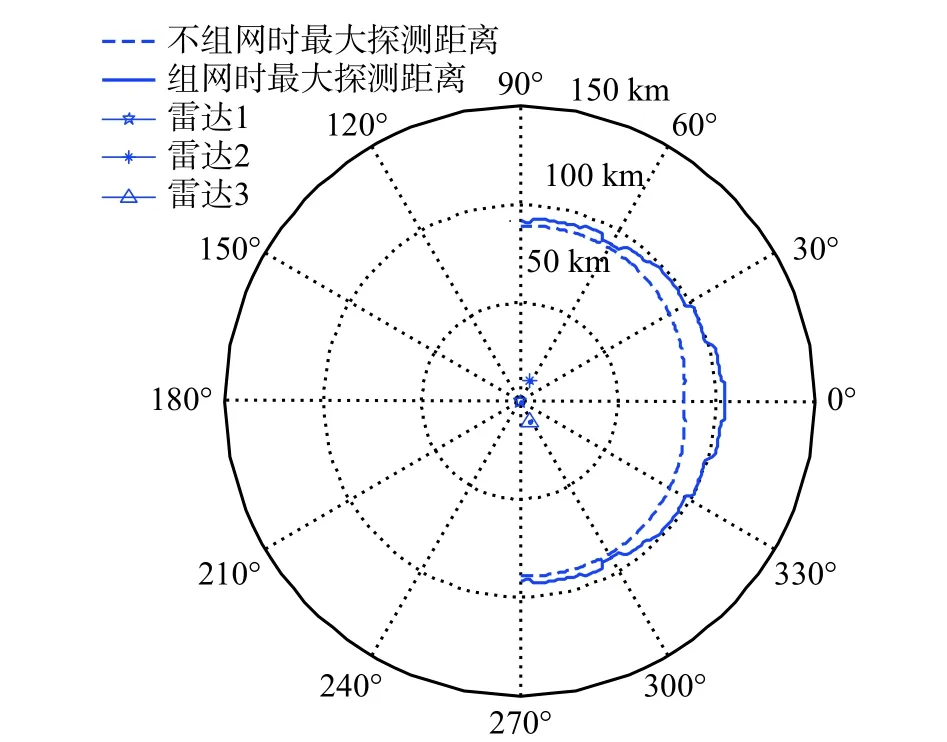
图3 目标航行姿态未知时的探测范围Fig. 3 Maximum detection range of unknown navigation attitude

图3 中，雷达组网对目标的探测范围为一段折线形成的包络面，该探测范围与不组网时相比增大了约11.20%；折线最远处距离雷达1 约105 km，处于雷达网的正东面，与不组网相比增大了约16.67%. 由于目标部分角度的RCS 较大，雷达组网后各雷达对目标的观测角度不同，探测距离相互补充，增大了对目标的探测范围.

4.2 假设舰船目标由南向北航行

此时目标的轴线与正北方向夹角为0°，雷达网对目标的观测范围以左舷为主，利用本文方法计算雷达网对目标的有效探测范围，结果如图4 所示.

图4 中，雷达网对目标的有效探测范围最大值约130 km，最小值约50 km. 由于目标左右舷约90°及舰尾方向RCS 较大，当目标处于雷达网南面时，雷达网对目标的观测方向以舰艏为主，最大探测距离较小；当目标处于雷达网北面时，雷达网对目标的观测方向以舰尾为主，最大探测距离较大；当目标处于雷达网东面时，雷达网对目标的观测方向以左舷为主，最大探测距离最大.

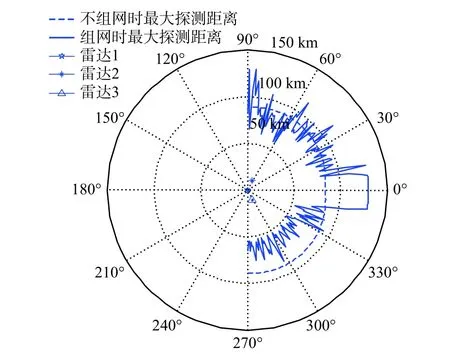
图4 目标由南向北航行时的有效探测范围Fig. 4 The effective maximum detection range of the target sailing from south to north

4.3 假设舰船目标由东向西航行

此时目标的轴线与正北方向夹角为90°，雷达网对目标的观测范围以舰艏为主，利用本文方法计算雷达网对目标的有效探测范围，结果如图5 所示.

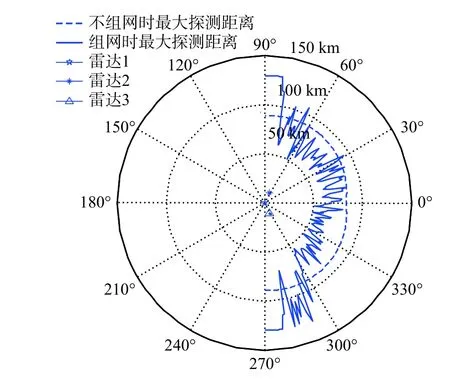
图5 目标由东向西航行时的有效探测范围Fig. 5 The effective maximum detection range of the target sailing from east to west

图5 中，雷达网对目标的有效探测范围最大值约128 km，最小值约50 km，且在大部分方位上小于90 km. 目标舰艏方向RCS 较小，当其由东向西航行时，雷达网对其有效探测距离较小.

5 结 论

蒸发波导条件下，目标处入射波的强度与高度有关，学者们研究了目标RCS 在高度上的分布对微波超视距雷达最大探测距离的影响，并建立了最大探测距离评估模型. 本文在此基础上，考虑目标RCS在方位角上的分布，建立了雷达组网时的探测范围评估模型，计算了三种不同情形下雷达组网后的探测范围，并通过与不组网时的评估模型相对比得出以下结论：

1)当目标运动姿态未知且两种评估模型的准确率相同时，雷达组网增大了雷达的探测范围. 具体而言，雷达组网使雷达的探测范围增加了11.20%，在特定方向上使探测距离增加了16.67%.

2)当目标运动姿态已知时，在极大提高评估结果准确性的前提下，雷达组网在部分方位角上增大了最大探测距离，同时在部分方位角上减小了最大探测距离. 从探测范围的角度证明了雷达组网的可行性和优越性，为微波超视距雷达的组网使用提供了理论支撑.

本文使用的舰船目标RCS 高度分布模型较为粗糙，下一步应着重研究舰船目标RCS 在蒸发波导条件下随高度分布的规律，建立更为精确的高度分布模型，进而提高微波超视距雷达组网探测范围评估模型的准确性.