让信息技术助力数学教学，实现深度学习

王燕

深度学习数学是学生形成数学核心素养的重要途径。翻转课堂是信息技术与教育教学深度融合的产物，是学生深度学习数学的助力。本文以“三角形内角和”为例，从课前预习、课堂学习和课后练习入手，详细阐述应用翻转课堂教学模式助力学生深度学习数学的策略。

2021年，基于中小学生课业负担和课后培训负担过重问题，“双减”政策应运而生，旨在切实发挥优质教育资源作用，使课堂教学提质增效。而随着时代的发展，信息技术已经成为一种越来越重要的教学手段和教育资源。当前，信息技术与学科教学的融合不断加深，各种新的教学模式也应运而生。翻转课堂是其中之一。这一教学模式不同于传统教学流程，以信息技术为支撑，辅助学生课前自主预习，课堂重点学习，课后自主练习，由此由浅入深地理解数学内容，锻炼学习能力，实现深度学习，切实地提高数学学习效果。众所周知，深度学习是思维的深入参与，需要学习者调动自己的高阶能力，在学习知识的过程中全身心地投入，实现知识建构、知识迁移、问题探究、辩证思考等有深度的活动和内容。在小学数学课堂中，自主学习是达成深度学习的重要前提，课堂学习是学生实现深度学习的关键，课后练习是学生实现深度学习的保证。基于此，在实施小学数学教学的时候，笔者利用信息技术翻转数学课堂，辅助学生课前预习、课堂学习、课后练习，实现深度学习，提高数学学习效果，切实落实“双减”政策。以“三角形的内角和”为例，具体应用的策略如下：

一、借助信息技术，指导预习

预习新知是学生学习新知的起步活动，也是学生初步认知新知的活动，更是学生在课堂上深入探究新知的基础。翻转课堂教学的应用调整了数学教学流程，前置学习于课堂，借助微课为学生提供了自主学习机会。所以，在实施数学教学的时候，笔者依据新知内容，录制微课，并将微课应用到课前，同时提出自学任务，指导学生自主学习，使他们初步认知新知，同时锻炼自学能力，为实现深度学习奠定基础。

在实施“三角形的内角和”教学之前，笔者围绕新知内容，以《名侦探柯南》为背景，录制了微课，呈现了不同的线索，引导学生进行探究。线索一：学习的内容会与三角形的哪部分有相关性？线索二：三角形的角的特性会与几个角有关？线索三：三角形的三个角究竟有何特性？在提出每一个线索后，都要求学生停止播放，将自己的思考写到任务单上，之后继续观看微课，根据微课讲解的内容和提示，有针对性地进行思考，完善任务单内容。

事实上，在思考每条线索的时候，学生会回顾已学知识，探寻知识间的联系;逐个分析数学信息，获取关键信息;提出猜测，利用操作进行验证。通过体验如此过程，学生可以对新知内容建构初步认知，积累学习新知的经验，顺其自然地锻炼自主学习能力。

二、借助信息技术，引导学习

引导学生学习是教师教学引导作用的具体体现，也是学生迁移知识储备和自学所得深入探究新知的必由之路，有利于学生从浅层认知走向深层认知，逐步实现深度学习，提高课堂学习效果。所以，在实施数学课堂教学的时候，教师要应用适宜的方式引导学生深度学习。

（一）创设情境，调动兴趣

建构主义学习理论指明了学习情境对学习活动重要性。情境是数学课堂不可缺少的一部分，是学生迁移已有经验走进课堂的桥梁。信息技术是创设情境的主要手段。且用信息技术创设出的教学情境具有直观性、动态性，契合小学生特点，便于调动学生的学习兴趣，促使学生自主探究新知。所以，在实施课堂教学的时候，笔者会利用微课创设教学情境。

在“三角形的内角和”课堂导入环节，笔者通过播放微课创设了游戏情境。首先展示出一个被遮挡了两个角的三角形，（停止播放）引导学生思考：“这是一个什么三角形？”在学生给出各种答案后，继续播放微课，随着遮挡物的移动，学生看到了另外一个角，接着，笔者追问：“这是什么类型的三角形？”此时，学生的意见不一，有了冲突，钝角三角形、直角三角形、锐角三角形，皆有人回答。笔者鼓励学生说明原因。一些学生迁移自学经验，借助三角形的内角和是180°表明自己的观点。而持相反观点的学生提出质疑：“为什么说三角形的内角和是180°？”笔者及时肯定学生的动脑行为和自主提问行为，并引导他们一起探究三角形的内角和是否是180°。如此教学，不仅使学生因体验情境产生了数学探究兴趣，还使他们通过体验情境，积极思维，迁移所学，有利于做好深度学习准备。

（二）引导探究，建构知识

探究是学生深度学习数学的重要方式。探究的过程，是学生迁移所学的过程，也是积极思维的过程，更是从数学现象获取数学结论的过程。从上文论述可见，学生通过体验自主学习活动和情境体验活動，初步认知了新知，迁移了学习经验，为教师进行教学引导提供了便利。教师在实施课堂教学的时候，可以基于学生的学习情况和重难点内容，应用适宜的方式对学生进行引导，使学生发挥自主性，深入探究，解决一系列问题，逐步理解数学知识，同时锻炼探究能力，提高数学学习效果。

“验证三角形的内角和”是“三角形的内角和”这节课的重点内容，是学生需要深度学习的内容。立足此内容，笔者在课堂上提出问题：“量1个角误差产生一点点，量2个角，误差再变大，量3个角误差会更大，那能不能想办法把三个角变成一个角呢？应该怎么变呢？”在提出此问题后，笔者引导学生与小组成员合作交流，想出恰当的方法解决问题。在小组交流的过程中，大部分学生迁移学习经验，碰撞思维，探究到多样的解决问题的方法。如撕拼法、折叠法。在学生合作探究后，笔者鼓励学生积极发言，展示本组探究到的方法。在此过程中，笔者根据学生展示的内容作出点拨，使学生加深理解。接着，笔者利用电脑的几何画板画出一个有魔法的三角形，和学生一起探究它的魔法在哪里？在探究的过程中，学生仔细观察什么在变，什么一直没有变。同时，给予学生提示：每个角度数的变化，内角和的变化。基于他们观察的情况，笔者提出问题：“在三角形变化的过程中，有没有发现哪个三角形内角和不是180°的？”学生迁移观察所得，轻松地给出否定的答案，从而证实三角形的内角和是180°。如此教学，不仅使学生切实地发挥了自主性，通过与小组成员的一次次合作，碰撞思维，解决问题，获取答案，由浅入深地理解数学知识，还使学生通过亲身体验，锻炼了思维能力，探究能力，有利于提高课堂学习效果。

（三）精准评价，促进发展

教学评价是课堂教学不可缺少的一部分，是贯穿课堂教学始终的活动。《义务教育数学课程标准（2011年版）》中阐明了教学评价具有激励作用，要求教师用好教学评价，促进学生发展。受到个性差异的影响，学生的数学学习情况是不同的。促进每一个学生发展是教师提高数学课堂教学的关键，也是教师实施教学评价的目的。精准评价是实现这一点的重要方式。大数据为教师提供了精准评价的依据。由此，教师在实施课堂教学的时候，可以以智慧课堂为依托，用好大数据，精准地对学生进行教学评价。

比如，在“验证三角形的内角和”探究过程中，笔者引导学生合作地操作平板电脑，将探究的方法上传到教师端。笔者则在教师端了解学生的探究情况，并利用相关APP生成数据，由此确定每个小组和全班学生探究情况。之后，对比每个小组此次探究情况和之前的探究情况，用发展的眼光发现学生的进步之处，同时发现不足之处。接着，利用平板电脑对每一个小组进行合作学习评价，赏识他们的进步之处，使他们获得满足感，同时指出合作探究不足，提出弥补建议，有针对性地查漏补缺，提高合作学习水平。

三、借助信息技术，分层练习

练习是学生应用所学解决问题的活动，是学生深入理解所学，锻炼应用能力的活动。因材施教是教师实施数学教学的基本原则，也是提高数学课堂教学质量的关键。因为学生具有个性差异，他们的数学学习水平是不同的。教师要立足学生的学习水平差异，设计难易程度不同的练习题，使他们都能获得解决问题的机会，尤其通过解决问题，加深对数学的理解，增强深度学习效果。基于此，笔者在讲解了新知内容后，利用希沃白板创设动画闯关游戏，呈现难度不同的练习题，引导异质小组中的不同学习水平的学生进行挑战。

在“三角形的内角和”这节课上，笔者利用希沃白板创设了五个关卡。第一关和第二关由低水平学生参与;第三关和第四关由中水平学生参与;第五关由高水平参与。具体过程入下：

第一关：我是小法官 。对的用手势“√”表示，错了用“×”表示。

1.钝角三角形的内角和比锐角三角形的内角和大。

2.三角形越大，它的内角和就越大。

3.“讲文明，树新风”这个三角形的牌子，它的内角和是180°。

闯关成功，进入第二关：

第二关：下列各组角是同一个三角形的内角吗？

1. 82°，95°，5°           2. 60°，70°，90°

同学们的判断既快又对，进入第三关：

第三关：求未知角的度数。

1.如图2所示，∠A=____

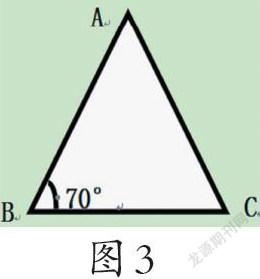
2.已知下面（图3）这个等腰三角形的一个底角，请求出它的顶角∠A的度数。

3.已知下面图形（图4）是等边三角形，请求出∠A的度数。

第四关：

1.有一个等腰三角形，其中一个角是50°，其他两个角分别是多少度？

2.有一个等腰三角形，一个底角是顶角的2倍，三个角分别是多少度？

3.有一个等腰三角形，顶角是一个底角的2倍，三个角分别是多少度？

第五关：拓展提升：观察图5，它们的内角和是多少度？

在学生闯关的同时，笔者就给出的答案进行点拨，并引出有关的数学知识点，使学生及时地查漏补缺，加深对所学的理解。

四、结语

综上所述，有效地将信息技术应用于数学课堂，便于学生通过体验课前活动、课堂活动和課后活动，实现深度学习，提高数学学习效果。所以，在实施小学数学教学的时候，教师要把握住恰当的时机，选用适宜的信息技术，调整课堂教学，采用多样策略，引导学生进行课前预习、课堂学习和课后练习，使学生迁移知识储备，发挥高阶能力，逐步探究数学内容，深度理解数学内容，锻炼学习能力，提高数学学习效果。

（吴淑媛）