基于时间序列统计模型的移动基站流量预测分析

刘文暄，曹秀娟，王嘉琪，黄崇政，袁皓涵

（1.山东科技大学，山东 济南 250031；2.西安欧亚学院，陕西 西安 710065）

近年来，随着移动互联网的爆炸式发展，基站的流量负荷问题变得越来越重要。 一方面，为了缓解流量高峰期基站负荷超量造成的网速减慢问题，就需要增加基站的载频数量，使其可以承担更多流量； 另一方面，受基站潮汐现象的影响，在某些时段，用户数量会大幅降低。 从长期来看，大部分基站的整体流量呈逐渐增加趋势。 在流量增长到一定程度时，动态开关载频已经无法满足要求，这就需要通过新建扇区或者基站来进行物理扩容。 物理扩容因涉及到采购资金、 总体布局等问题，规划时间非常长，所以需要提早预估基站物理扩容的时间，从而可以更早地进行规划和设计。

通过分析，可以看出，除了节假日，每周的数据流量基本都具有周期性，因为用户量一直增长，每周的流量总量增长，因此可以忽略影响。 单一的算法难以直接预测周期性增长数据，因此把这种预测拆分开来预测每周流量的整体增长变化情况[1]。

1 利用leaf-wise 算法优化短期流量预测

短期预测采用1eaf-wise 算法进行采样优化： 保留上行流量梯度较大的样本，对于流量变化趋势较小的样本进行抽取采样。 同时在计算增益时，对上行流量变化趋势较缓的样本增加权重系数[2]。

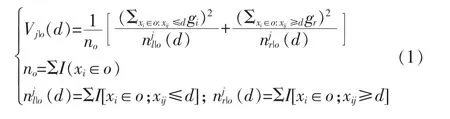
其中带来的增益可以定义为式中：Vj|o（d）为最大增益；no为分位点个数；x 为平方损失减少值； i 为单棵树的节点； j 为全局重要度特征； o 为根据j 将数据分为左右子节点的训练集； gi为上行流量数据； gr为下行流量数据。

若使用单边梯度采样算法 （Grandient-based One-Side Samp1ing，GOSS） 后，增益定义为

再进行特征抽取，将互斥特征绑定在一起，从而减少特征维度。 运用1eaf-wise 生长策略进行预测，因其最大增益不变，且无需重复计算。 其短期预测结果见第43 页表1。 从预测结果可以看出，使用1eaf-wise 算法预测的结果相对可靠，可用于各个小区小时级上行和下行流量的短期预测。

表1 短期预测结果

2 长期预测原始数据的平稳性处理

考虑到小区上下行流量很容易受到地区或者时间的影响，在使用1eaf-wise 算法进行长期上下行流量预测时，由于1eaf-wise 算法对周期性数据的预测结果存在一定的偶然误差，所以可建立ARIMA 模型进行流量的长期预测。 ARIMA 模型要求所使用的的序列数据必须是平稳的，通过对原始数据进行分析，发现小区流量序列存在不平稳情况，为得到平稳的原始序列，所以在构建ARIMA 模型之前有必要对小区流量数据进行ADF 检验。

图1 为差分处理前后的ADF 检验结果。 在图1-a 中，原数据T 统计量大于任何置信度的临界值，且p 值大于0.05，因此，确定该序列是非平稳的，需要对序列进行一阶差分处理。 在图1-b 中，差分处理之后，T 统计量小于5%与10%的置信度的临界值，且p 值小于0.05，说明在差分处理后，序列平稳。

图1 差分处理前、差分处理后的ADF 检验结果

3 ARIMA 模型的参数确定及长期预测结果

ARIMA 模型常用AIC 准则与BIC 准则进行参数确定。 由于AIC 准则存在一定的不足之处，其计算公式为

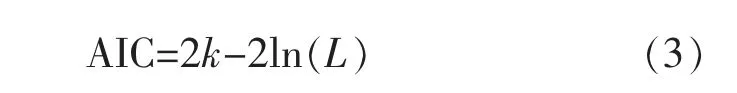
式中： k 为参数的数量； L 为似然函数。

当样本容量很大时，在AIC 准则中拟合误差提供的信息就要受到样本容量的放大，而参数个数的惩罚因子却和样本容量没关系。 BIC 贝叶斯信息准则弥补了AIC 的不足，其公式为

利用AIC 和BIC 可以选取模型最佳的p，q 组合，应当选取AIC 和BIC 值达到最小的那一组为理想阶数。 模型参数结果见图2。

图2 模型估计结果图

通过调整p 和q 参数，使AIC 与BIC 的数值达到最小。 经过比较，p=0，q=1 为理想阶数。 综上，建立ARIMA（0，1，1）的模型进行求解，其长期预测结果见表2。

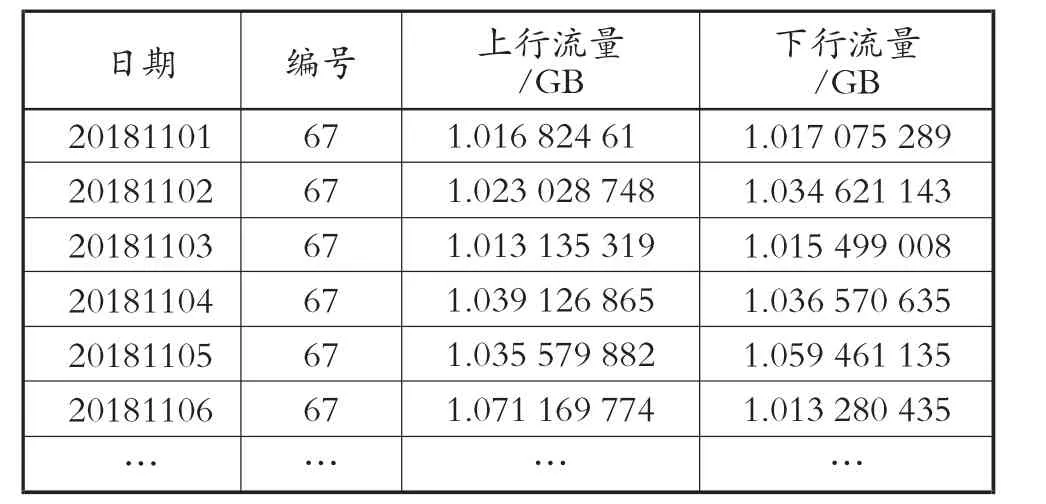
表2 长期预测结果

4 误差分析

在预测出长期结果后，还应该进行检验分析。从ARIMA 模型的预测结果可以看出，一阶差分的时间序列的均值和方差基本平稳，但是还应比较二阶差分后时间序列的效果是否更佳。 自相关和偏自相关结果见图3，可以看出自相关和偏相关都缩小至0，即为一个混合模型[3-4]。将差分次数d 的值设置为2，对该模型做D-W 检验，因为自相关系数的值介于-1 和1 之间，当DW 值显著地接近于0 或4时，则存在自相关性。 而接近于2 时，则不存在（一阶） 自相关性。 最终得出的检验结果为2.0242，接近于2，残差序列不存在自相关性，说明二阶差分后的时间序列与一阶差分相差不大，并且随着时间的推移，二阶差分后的时间序列的均值和方差几乎保持不变。

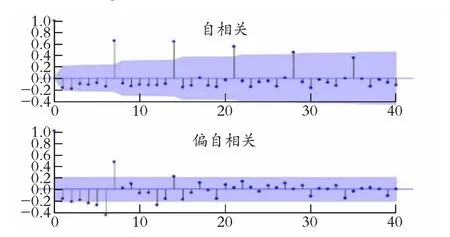
图3 自相关图和偏自相关图

5 结束语

现在是大数据的时代，几乎可供人们使用的数据都和时间有关系，这就是时间序列数据。 本文基于1eaf-wise 算法以及ARIMA 模型建立了短期和长期流量预测模型。 向量自回归模型筛选能力，其四元时间序列的模型筛选正确率明显高于二元时间序列。 本文所建立的模型适用于金融、 天气情况、 销售量、 股票的预测等很多方面。