基于暂态能量流的MMC-HVDC系统故障建模及仿真分析

2022-06-01陈力绪许建中赵成勇贾秀芳

华北电力大学学报(自然科学版) 2022年3期

严俊，陈力绪，许建中，赵成勇，贾秀芳

(华北电力大学电气与电子工程学院，北京 102206)

0 引言

分析能量的分布与转移规律，是进行大规模工业系统规划的前提之一，也是监控、维护与优化系统的重要基础[1]。交流系统中的暂态能量流(Transient Energy Flow, TEF)用以描述元件的机电暂态能量，是分析交流系统稳定性问题的手段之一[2]，也用于评估次同步振荡强弱以及振荡溯源[3]。在采用扩展性良好、谐波输出低和开关频率低[4]的模块化多电平换流器(Modular Multilevel Converters, MMC)构建的高压直流(High Voltage Direct Current, HVDC)输电系统[5，6]中，若由无故障穿越能力的半桥型子模块(Half Bridge Sub-Modular, HBSM)构成的MMC，分析极间短路(Pole to Pole, P2P)故障演化过程中的暂态能量流动态势，可为暂态工况下设备的精细化设计及故障抑制与清除手段提供理论依据[7]；而且对盈余的暂态能量合理规划未来有望服务于基于换流器的储能设计方案[8，9]。目前针对直流TEF的研究较少，与暂态能量直接相关的研究有故障清除时直流断路器吸能支路中避雷器的能量参数设计[10]，少量学者从能量与功率维度对保护判据进行研究，文献[11]认为相较其他暂态特征，对比线路两端短时能量的差异，判断小电流接地方式下单极对地故障线路的准确性更高。文献[12-13]利用高低频段暂态功率的比值与极性，或者谐波能量构成边界保护元件并构造方向辅助判据，结合保护启动及故障选极元件构成基于暂态功率的单端量保护方案。还有学者通过MMC、直流线路及平波电抗器中暂态能量离线仿真数据，根据暂态能量消涨态势完成了张北直流电网故障传播规律及影响因素的定性分析[14]。在此基础上，文献[15]提出了兼顾暂态能量抑制技术性及经济性能指标的设备参数优化模型，提高了系统中桥臂电抗、平波电抗与故障限流器的限流利用率。此外，文献[16]考虑到故障穿越期间并网风机不间断注入功率，提出了耗能电阻分级投入的能量抑制策略，与风机内部的斩波电阻的配合共同改善功率盈余状态。

以上文献侧重分析或解决特定工程问题，而故障机理分析领域，主要聚焦于故障电流的解析计算。通过构建单相定值RLC等效放电电路来分析瞬态过程，该方法已成为部分双端、多端或直流电网中短路电流计算的基础[17，18]。基于此，MMC与其他换流器故障对交流和直流系统的影响，及接地方式不同对单极短路故障特征的影响被相继分析[19，20]。文献[21]利用拟合及剩余能量反推的方法不断获取状态量初值，提出了计及控制系统影响的精确故障电流计算方法。然而，采用定值RLC串联等效电路，将使桥臂内部元件的部分暂态特征丢失，难以得到桥臂内部能量的流动情况。本文基于暂态能量流及变化量守恒与不能突变的性质，建立了计及HBSM动态行为的等效数学模型，求解MMC闭锁前后的状态方程可得到精确故障电流与关键元件暂态能量值，并在PSCAD中仿真验证其精度。

针对直流电网，若精确获取每个MMC中的故障电流通常需要复杂的计算过程。基于具体工程参数的仿真方法更适合受多种因素影响的高压直流输电网的故障特征分析。本文提出了一种通过分析不同部件和区域(或分支)吸收或释放的电磁暂态能量的分布，来识别影响其分布因素的方法。该方法可以通过TEF递推计算实现故障电流的定量分析。基于TEF分布，通过重构投入电容的数目，可以在HBSM电容允许的电压波动范围内限制电容能量的释放，达到延迟闭锁时间的效果。

1 暂态能量及暂态能量流的定义

直流系统中暂态能量流E(ti)是以暂态起始时刻t0为基准，描述任意时刻某部位或某元件上能量的吸收或是释放情况，也即该元件当前时刻对应的能量与初始时刻的能量之差。桥臂中的电感、HBSM电容、电阻以及阀侧交流系统与MMC直流出口的暂态能量流，分别为EL(ti)、EC(ti)、ER(ti)、Eac(ti)、Edc(ti)，计算公式如表1所示。

表1 暂态能量定义表达式Tab.1 Definition of components transient energy and variation

表1中，任意时刻ti=t0+i·Δt，Δt为时间间隔，i=1,2,3,…。E(ti)没有正负，有吸收与释放能量之分，正方向如图1所示。TEF变化量ΔE(ti)为两个相邻时刻TEF之差，可以反映单位时间内E(ti)的变化趋势，表征能量转移的快慢。

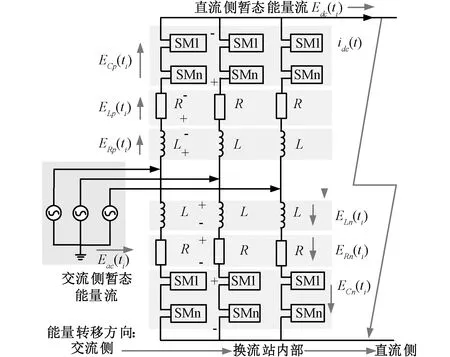
图1 MMC中的暂态能量转移正方向示意Fig. 1 Positive direction of transient energy transfer in MMC

不同的Δt将使E(ti)及ΔE(ti)不同，因此在计算或仿真时，步长选取应尽可能地反映系统能量的瞬时变化情况。Δt应小于HBSM投切的最短时间[22]。根据第四章中所述的仿真参数，稳态时a相上桥臂的EL_a(ti)及ΔEL_a(ti)如图2所示。

图2 a相上桥臂电感的EL_a(ti)及ΔEL_a(ti)Fig. 2 EL_a(ti) and ΔEL_a(ti) of inductor in bridge arm of phase a

图2中，若关注的时间段较短，可观察到ΔEL_a(ti)由条形图组成。EL_a(ti)曲线斜率正负值在A与B点处改变，与ΔEL_a(ti)的过0点对应；ΔEL_a(ti)在点C和点D处达到最值，与EL_a(ti)曲线中上升与下降速率最快的情况相对应。通过对更长时间段对应的能量流进行观察，电感元件上能量的吸收与释放保持平衡。

2 基于能量守恒的MMC故障建模及求解

本文所提计算模型基于P2P故障建立，因为P2P故障时双极均不能正常运行且故障的暂态过程发展更为迅速[23]。将闭锁视为直流短路故障的保护策略，含断路设备的研究将后续展开。

2.1 考虑HBSM投切的MMC换流器等效模型

分析HBSM电容的动态切换行为时，应考虑到调制策略[23]以及交流电压对HBSM电容放电的影响。根据能量守恒以单相的上桥臂为例，等效电路如图3所示。

图3 考虑HBSM投切的单相上桥臂的等效电路Fig. 3 Equivalent circuit of upper bridge arm in single-phase considering HBSM switching

图3中，t时刻单相共导通N个HBSM，xp,nj(t)为三相上、下桥臂导通的HBSM数量，p与n代指上、下桥臂，j为a,b,c三相。假设每个子HBSM电容C0的电压uC0(t)均相等。桥臂中电容元件电压up，nj(t)可以表示为

up,nj(t)=xp,nj(t)×uC0(t)

(1)

若将单相的桥臂等效成图3右侧所示的形式，等效电容Ceq(t)的取值将跟随导通状态的HBSM数量xp,nj(t)的变化而变化

(2)

式中：k为调制比；三相调制波ukj(t)可以表示为ukj(t)=kusj(t)；usj(t)为三相电压。

图3中等效前的EC(ti)和等效后的ECeq(ti)可表示为

(3)

t0时刻的等效电容电压up，nj(t0)可表示为导通HBSM数量xp,nj(t0)与uC0(t0)的乘积。由于能量守恒，桥臂的能量在转换前后保持不变，t0+Δt时刻对应导通HBSM的数量是xp,nj(t0+Δt)，则up，nj(t0+Δt)可以写成

(4)

此处式(4)仅适用于多电平MMC场景。将式(1)代入式(3)，可以得到等效电容Ceq(t)为

(5)

故障后usj(t)与ukj(t)将不可避免地出现幅值与相位的差异，影响HBSM电容放电，在计算桥臂电流i1(t)～i6(t)时采用RLC等效模型无法将该过程考虑在内。时变的等效电容Ceq(t)可以用于描述考虑HBSM动态行为的MMC等效电路。

2.2 闭锁前暂态状态量的计算方法

本节将交流系统馈入和各个桥臂上HBSM电容动态行为考虑在内，计算P2P故障后的故障状态量。按照2.1中的等效方法将导通的SM电容等效为时变电容后，MMC等效电路如图4所示。

图4 闭锁前的MMC等效电路Fig. 4 Equivalent circuit of MMC before blocking

根据图4中的等效电路，列写KCL方程。

(6)

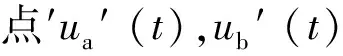
(7)

暂态状态量i1(t)～i6(t)和uC1(t)～uC6(t)的微分表达式为

(8)

经整理，可以得到

(9)

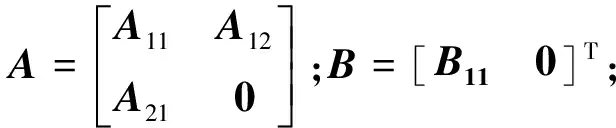
(10)

(11)

(12)

每个元素为计及HBSM动态投切的等效电容。Β11记作

(13)

根据表1中的计算公式，可得到EL(ti)、EC(ti)、ER(ti)、Eac(ti)、Edc(ti)。此外，对于A21中的Ceq(t)表达式，可表示为

(14)

当导通HBSM数量发生变化的桥臂，更新矩阵A即可求解。闭锁前的状态变量和TEF求解过程将在2.4中的流程图中给出。

2.3 闭锁后暂态状态量计算方法及求解流程

MMC闭锁后，所有HBSM电容均被旁路，并停止放电。短路电流主要由桥臂电抗的续流电流和交流系统馈入的电流组成，相应的等效电路如图5所示。

图5 闭锁后的MMC等效电路Fig. 5 Equivalent circuit of MMC after blocking

闭锁过程分为三个阶段：(1)初始阶段；由于闭锁前的放电过程，在i1(t)～i6(t)中存在大的非周期性分量，二极管均导通。(2)过渡阶段；由于电阻的存在i1(t)～i6(t)断衰减。(3)新稳态阶段；当i1(t)～i6(t)衰减至0 kA时，二极管关闭。三个阶段仍将HBSM投切考虑在内，分析如下。

第一阶段时，式(9)将改写为

(15)

第一阶段时A′与B′中的元素均为常数；第二阶段时二极管关闭并进入高阻状态，桥臂等效电阻为

Rarm=R+xp,nj(t)Roff≈xp,nj(t)Roff

(16)

式中：Roff为二极管关断时的电阻值。

第三阶段时，当关断二极管的正向电压超过阈值电压UT0时，相应的电阻表示为

Rarm=R+xp,nj(t)Ron≈R

(17)

式中：Ron代表二极管导通时的电阻值。

2.4 全暂态模型的求解过程

求解全暂态模型可获取桥臂电流、直流故障电流和系统各部分TEF，其步骤如图6所示。

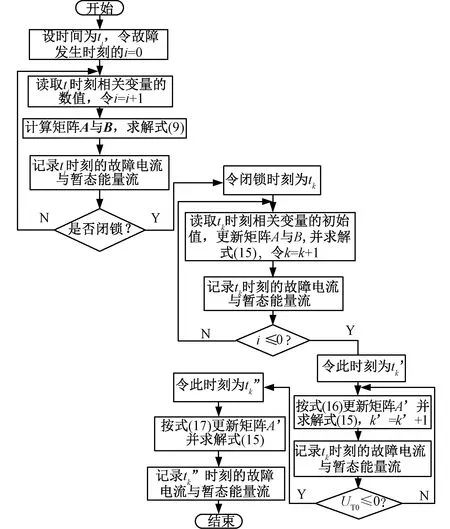
图6 暂态过程中短路电流及TEF求解流程Fig. 6 Solution flow of short-circuit current and TEF in transient process

Step1:自故障时刻起，读取每一时刻的状态量数值；更新参数矩阵A和B，代入并求解式(9)，得到i1(t)～i6(t)，记录该时刻的故障电流与TEF数值，直至闭锁。

Step2: 达到闭锁条件并实施闭锁动作后，进入第一阶段，更新参数矩阵A′和B′后代入求解式(15)，并记录该时刻的故障电流与TEF数值。

Step3: 判断桥臂电流与二极管端电压；若进入第二阶段，则依据式(16)更新参数矩阵A′；若进入第三阶段，则依据式(17)更新参数矩阵A′；重复Step2中的求解过程，直至进入下个状态若干时间后结束。

图6中对应Step1求解式(9)时，均需读取每一时刻i1(t)～i6(t)，并根据式(6-7)得到uj′(t)用以计算调制波。认为故障后较短的时间，与MMC站级控制系统所包含的多个PI环节，使调制波在短时间内不会明显失真[21]。调制比k和相角δ可以被求解为

(18)

(19)

式中：P和Q分别为交流侧传输到直流侧的有功功率和无功功率；X为交流系统等效阻抗。当发生高阻故障、系统中阻抗参数较大或是仅关心1-2 ms内故障特性时，不必多次求解usj′(t)，可直接求解式(11)，在计算速度与精度之间进行取舍。

3 基于暂态能量流的故障特性分析

暂态能量守恒为MMC-HVDC系统换流器暂态模型中HBSM的等效提供了条件，可精确求解桥臂电流。本节将面向直流电网，基于暂态能量流的变化规律分析故障特性。

3.1 暂态能量流在直流电网中的应用

柔性直流电网中影响直流短路故障电流的因素(如故障位置、网路拓扑、系统各部分参数，控制策略等多重因素)比双端系统中更复杂，导致第2章中所述的暂态建模及求解方法面临三个主要挑战：第一，多换流站之间存在耦合关系，无法采用简单叠加原理获得MMC桥臂电流和故障线路直流电流。第二，多端直流电网暂态数学模型中的状态变量维数多，建模及求解过程复杂，且难以在大规模精确建模与快速求解中取得平衡。第三，直流电网暂态建模需要依据直流电网拓扑、MMC变换器等效参数、系统运行模式和控制方式等建立对应的微分方程组，以上因素一旦改变，此模型中的微分方程就要重新建立，无法有效地定量分析出各因素对其故障电流演化规律的直接影响结果。

为了削弱系统规模、高计算精度和效率之间的冲突，提出了基于仿真的暂态能量流分析方法。该方法，可根据元件的TEF、元件具体参数及上一时刻电流值即可经过递推计算得到流过该元件的故障电流值。以桥臂电感L为例，电流iL(t)为

(20)

能量递推计算不需每次更新数学模型中的参数矩阵，无论是数据存储量和计算量，还是计算速度都小于第2章中的方法，适合用于直接求解复杂多端直流电网中的故障电流。但该递推计算无法实时的计算暂态状态量，而且依赖仿真参数，仅适合分析具体的工程参数。

3.2 一种暂态能量抑制策略

HBSM电容是暂态能量的主要来源，若减少HBSM电容投切数目N，将部分EC(t)存储在HBSM电容中，可减少短路电流。设定投切数目为kset·N，系数kset≤1将抬升uC0(t)，考虑波动率ε的EC(ti)为

(21)

kset=1/(1+ε)

(22)

该策略通过改进如图7所示的控制系统实现。

图7 能量抑制方法的原理与实现方法Fig. 7 Control and implementation of the proposed energy limiting strategy

检测到故障后触发能量抑制环节，重构N将减少xp,nj(t)，减少MMC向直流侧的释能。图6所示的流程即可计算故障电流，其中N应写为N′=kset·N。该方法不影响稳态时正常运行，为闭锁保护争取时间，且无需额外限流设备，不增加故障电流抑制的成本。

4 仿真验证

MMC-HVDC输电系统的详细参数如表2所示。

表2 系统参数设置Tab.2 System parameter setting

t=1 s时令MMC直流出口处发生P2P短路故障，初始值uc1(t0)～uc6(t0)和i1(t0)～i6(t0)如表3所示。

表3 uc1(t0)～ uc6(t0)和i1(t0)～ i6(t0)的初始值

4.1 MMC闭锁前后的理论值与仿真值对比

当Rf的值分别取0.03 Ω、10 Ω和100 Ω时，对比直流侧故障电流idc(t)的理论值和仿真值，结果见图8(a)。误差较大的情况出现在Rf=0.03 Ω时，对该条件下的i1(t)～i6(t)进行如图8(b)所示的理论值与仿真值对比，图8中非实线的曲线线为电流仿真值，实线为理论值。

图8 故障电流理论值与仿真值对比Fig. 8 Comparison of fault current simulation and calculation value

图8(a)中所示，Rf较小时直流侧电流idc(t)快速上升度且峰值最大，同时Rf=0.03 Ω对应的误差为0.98 kA，最大误差不超过4.08%，其结果小于文献[24]中采用的计及HBSM电容动态行为均值等效RLC模型计算误差。图8(b)中，a相上桥臂i1(t)误差最大，不超过5.03%，其余Rf取值时的误差如表4所示。故障后，尤其是Rf较小时电压电流骤变，控制系统的修正作用在仿真结果中有体现，而理论分析中并未考虑在内，因此两者的结果存在一定的误差。

表4 不同Rf时i1(t)～ i6(t)理论与仿真值最大误差对比

对比不同Rf取值下的调制波，将调制波仿真值与理论值进行对比，以a相调制比为例，波形对比如图9所示。

图9 不同Rf时单相调制波的理论值与仿真值对比Fig. 9 Comparison of simulation value and theoretical value of Modulated wave in phase a under different Rf

图9中，高阻故障时调制比k在故障后5 ms仅抬升4.8%，认为调制波波形不发生明显的失真，此时计算流程中将k视为定值，相比之下计算加速比为1.14。

对比E(t)的理论值和仿真值，最大误差百分比如表5所示。当Rf=0.03 Ω时，EC(t)误差δ1大于Rf=10 Ω时的δ2、100 Ω时的δ3，不超过6.86%。

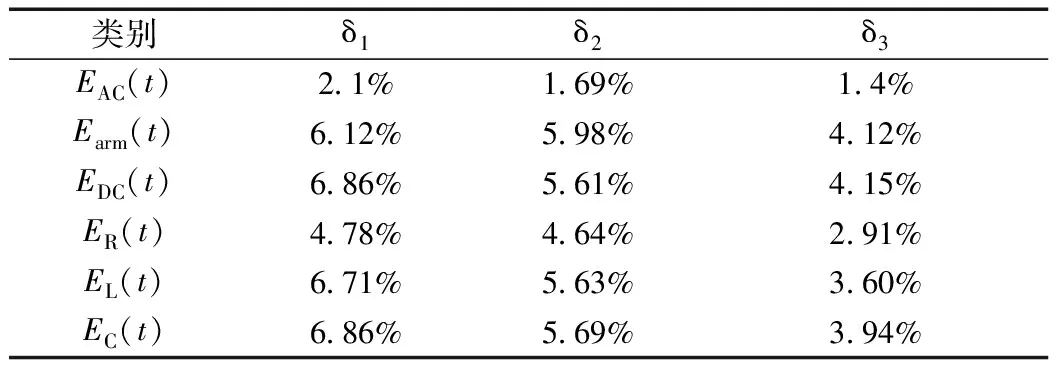
表5 不同Rf值下TEF最大误差

据表5中数据，认为E(t)误差较小可以反映E(t)的性质。故以下采用仿真值来分析不同Rf对关键元件ΔE(t)的影响。首先分析不同Rf时，HBSM电容的EC(t)与ΔEC(t)，如图10所示。

图10 不同Rf时电容元件上暂态能量及TEF分布图Fig. 10 Transient energy and TEF diagram on capacitive elements under different Rf

图11 不同Rf时桥臂电感上的暂态能量及TEF分布图Fig. 11 Transient Energy and TEF diagram on arm reactors under different Rf

相较稳态时电容元件的能量流，不同Rf时的EC(t)，在故障后5 ms内明显增长，且均为负值表示电容总体上表现为释放能量；Rf越小，释放的能量越多，释放的速率越快，这与图10(b)中的ΔEC(t)变化相呼应。当Rf=0.03 Ω时，ΔEC(t)在故障后2.48 ms达到峰值，此时对应的EC曲线上升速率达到最大；当Rf=10 Ω时，在(1.001 52,-0.021)处EC(t)曲线上升速率达到最大；当Rf=100 Ω时，在0.53 ms后，ΔECmin仅-0.003 7 MJ/μs，对应的EC(t)曲线上升速率达到最大，且EC(t)的最小值对比稳态时相差约3.2 MJ。

桥臂电感上TEF的如图11(a)所示，稳态时能量流在0.315～0.317 MJ之间波动，EL(t)均为正值表明故障后桥臂电感吸收能量，且随着Rf增大吸能总量及速率降低。

当Rf=0.03 Ω时，t=2.5 ms时ΔEL(t)=0.061 8 MJ/μs，对应的EL(t)曲线斜率最大；当Rf=100 Ω时，仅在0.1 ms内，时ΔEL(t)上升至最大值0.008 2 MJ/μs，其变化率远小于Rf=0.03 Ω时的值。

电阻包括桥臂电阻和Rf，ER(t)与ΔER(t)变化情况如图12所示。

图12 不同Rf时电阻元件暂态能量与暂态能量流分布图Fig. 12 Transient energy and TEF diagram on reactance under different Rf

图12(a)中ER(t)曲线较稳态时增加，图12(b)中，ΔER(t)为负值表示电阻元件持续吸收能量；Rf=0.03 Ω时的增幅更大增长更快，与图12(b)中ΔER(t)波形相符。随着Rf的增大时间常数减小，故障电流中的非周期分量更快地消失，而较小的Rf消耗的ER(t)较少，将有较多的能量在其他元件中储存或转化，因此电阻元件适合用于短路能量的消耗和暂态能量峰值的降低。

最后对比MMC闭锁后的理论值与仿真值。闭锁后直流侧电流理论值与仿真值的最大误差均在第一阶段结束时刻取得，分别为5.19%，3.88%和3.16%。Rf=0.03 Ω时，在故障后1.89 ms时，a相上桥臂闭锁，直流侧故障电流达到峰值，此时直流侧电流理论值与仿真值误差最大，但仍在合理范围内。

4.2 故障电流递推计算值与仿真值对比

Rf=0.03 Ω时各关键元件E(t)曲线如图13所示，当t=1 s时，电容元件共储存23.46 MJ；当t=1.001 s时，A1(1.001，20.5)，B1(1.001，3.0)；EC(t)与EL(t)重合点A2处为25.4 MJ，B2处ER(t)消耗1.7 MJ；当t=1.005 s时，A3(1.005，23.6)，B3(1.005，3.3)，C3(1.005，2.9)，其中2.9 MJ被电阻元件消耗；以上三种元件的能量流TEF之和在23.46-24 MJ之间，验证了3.1节中所提能量守恒的性质。

图13 Rf为0.03 Ω时各关键元件中能量分布Fig. 13 Energy distribution in key components when Rf is 0.03 Ω

图14所示为Rf=0.03 Ω时i1(t)～i6(t)计算值与仿真值的对比，其中虚线计算值，实线为仿真值。由递推计算得到i1(t)～i6(t)时，误差并未受到过渡电阻不同的影响。

图14 当Rf=0.03 Ω时i1(t)～i6(t)计算值与仿真值Fig. 14 Calculated value and simulation value of bridge arm current when Rf is 0.03 Ω

由图14可知，最大误差出现在i3中，仅为1.19%，与4.1中桥臂电流理论值的最大误差相比个更小。递推计算耗时远高于求解非线性方程并更新矩阵耗时，故递推计算在分析复杂多端合直流电网的故障特性时有优势；然而该方法依赖特定工况的仿真值，其结论不具备普适性。

4.3 直流电网中极对地故障时的TEF特征分析

为了提取MMC-HVDC-Grid的TEF的分布特征及其与直流故障演化过程之间的对应关系，根据表6中的参数，搭建了如图15所示的四端柔性直流电网[25]TEF仿真模型。

表6 四端MMC-HVDC仿真模型具体参数配置

该模型中暂未考虑闭锁保护与故障的隔离，极对地(Pole to Ground, P2G)故障点的设置和线路中初始能量流方向如图15所示。

图15 四端直流电网仿真模型Fig. 15 Four-terminal HVDC-Grid simulation model

4.3.1 同一线路不同位置P2G故障

图16对应故障点1-3时各个换流站的TEF分布图。T1～T15为稳态阶段，T15为故障时刻，T15～T55为故障后6 ms的暂态阶段，其中55个采样点的单位时间长度为0.15 ms。

图16 同一线路中不同故障点故障时的TEF分布Fig. 16 Overall TEF at different fault points in the same line

由图16可知，故障后3 ms内，距离故障点最近的换流站1中的EC,1(ti)是∑EC,x(ti) (x=2,3,4)的6-13倍，EL,1(ti)是∑EL,x(ti) (x=2,3,4)的15倍以上。Eac,1(ti)的波动范围不超过其故障前的稳态值的20%，送端换流站的交流侧暂态能量流波也在稳态值的20%以内，认为交流侧能量受到换流站系统直流侧故障的影响较小。故障3 ms后，相邻线路直流输入能量Edc2,1增大为故障前的3倍，表明相邻线路l12流向故障线路l14的瞬时功率在故障后迅速增大。这是MMC-HVDC四端环网与双端系统区别显著的TEF特征。

4.3.2 故障点位于不同线路

图17反映了故障点位于不同线路以及多点故障后的TEF分布情况。

图17 故障点位于不同线路上时的TEF分布Fig. 17 TEF when fault points are located on different lines.

图17(a)和(b)分别对应故障点1和5P2G故障时的TEF分布图。故障点4与故障点1距离换流站1的距离相同且均位于两个输送功率的换流站，对比图16(a)与图17(a)，换流站1的站内各元件TEF变化情况基本一致，但直流线路中的TEF的变化情况差别很大。在相似的故障点5与故障点2的TEF分布情况中，该规律同样存在。为了判断图17(c)与图16和图17(b)中所示单故障点TEF的差别，进行相似度分析，如表7所示。

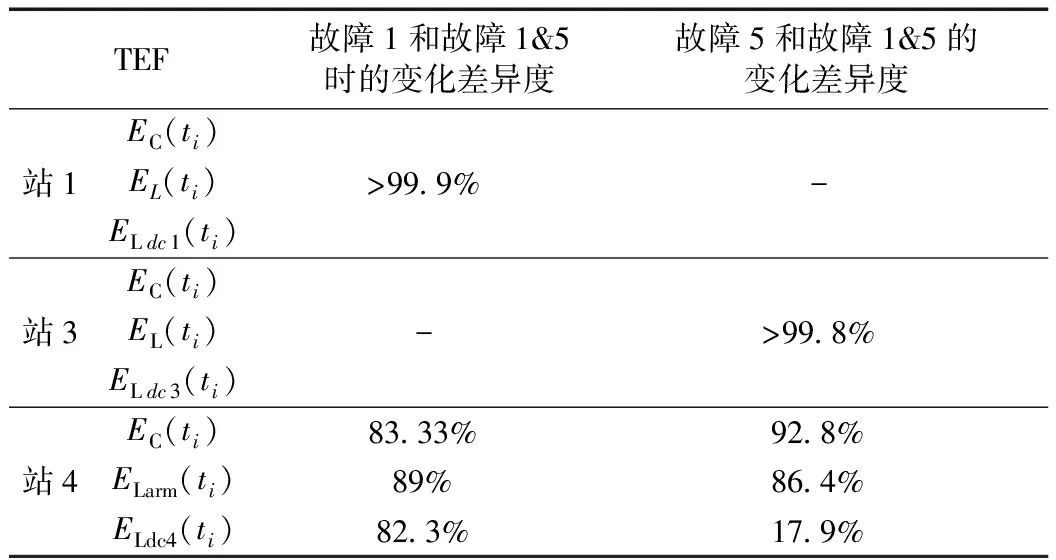
表7 单点故障与多点故障的TEF相似度分析

表7中多点故障线路的ΔEL(ti)时空分布余弦相似度仅17.9%，而其余故障线路中的换流站TEF时空分布与其所处线路单独故障时相同。故障线路中至少有一端换流站的故障情况与单线路故障时一致，利用交点换流站在多线路故障时的特殊性，可以为多线路故障的检测提供帮助。

4.3.3 线路TEF变化量特征分析

以故障点2发生P2G故障为例，对不同线路提供的能量占故障线路总能量的比例进行分析，结果如图18所示。

图18 l12 向l14提供能量占比及电流波形Fig. 18 Proportion of TEF provided by l12 to l14 and fault current

由图18(a)中可知，稳态时与故障后从相邻线路l12流入线路l14的能量占比均小于20%，且故障点1和3故障时同样存在该比例关系，故障线路两端的换流站对故障的影响程度最大。

4.4 能量抑制策略的仿真验证

将所提能量抑制策略应用于图15中的直流电网，假设故障发生于1 s时，检测时间为1 ms。以换流站1为例，i1(t)～i6(t)的闭锁值为6 kA，采用能量抑制策略后idc(t)波形如图19所示。

图19 减少HBSM电容投入的限流效果图Fig. 19 Current limiting effect diagram of reducing the input of sub module capacitance

当kset在0.7～1之间取不同值时，闭锁前的idc(t)均下降。实际工程中ε最大为15%[23]，故kset取0.86～1。当kset为0.86时，idc(t)可下降1.85 kA并延迟闭锁时间0.7 ms。已知，MMC中IGBT具有脆弱性，在过流环境下运行不得超过1 ms，所以该策略在安全运行的基础上为下一步的保护或故障隔离创造条件。