水力自控斜轴式闸门研究

闫旭胡秀华董小花魏汇庆邵亚茹王春堂

(1.泰安市王家院水库管理服务中心，山东 泰安 271018；2.泰安市水利局，山东 泰安 271018；3.滨州市引黄灌溉管理服务中心，山东 滨州 256600；4.山东农业大学，山东 泰安 271018)

引言

水是生命之源，万物离不开水。古往今来许多城市都依水兴起，水为城市注入活力，也是城市的生命线。而水闸作为城市河道的重要建筑物之一，在对城市防洪、供水等方面起着非常重要的作用，尤其在我国北方地区，常被用在城市河道中，用来改善河道常年缺水或少水的状况。为了满足社会变化的发展需要，水闸应具有简单灵活、方便使用等特点，而水力自控斜轴式闸门便很符合这一要求。该闸门目前尚未应用于实际当中，但较传统闸门而言，其具有操作灵活、制造方便、运行安全可靠、可节省电力与劳力、造价与管理维修费用低等优点。水力自控斜轴式闸门模型如图1所示。

图1 斜轴式闸门模型

水力自控斜轴式闸门是在平板闸门的基础上，将其向上游倾斜一定角度，利用上游来水的水压力及闸门自重，在一定流量条件下，依靠水压力实现自动启闭的新型闸门。该闸门适用于以下几种情况：上游来水流量过大，需及时宣泄洪峰流量；偏僻山区或无电地区；田间灌溉工程；城市水利工程[1]。由此可见，水力自控斜轴式闸门具有很大的发展空间，推广和使用该闸门是十分必要的，且具有重要的工程意义。

本文研究的水力自控斜轴式闸门是一种水力自动闸门，最常使用的水力自动闸为水力自动翻板闸门。在国内，从20世纪中纪以来，由于水利部门的重视与发展的需要，使得翻板闸门在防洪、发电、航运等方面得到广泛应用[2]。辽宁省本溪市是应用水力自控翻板闸门较早的地区，其应用推动了区域水电站的开发与建设和国内水力自控翻板闸门的应用与大力发展[3]。水力自控翻板闸门陆续被应用在越来越多的地方，如南方地区的中小型闸坝，山区水库溢洪道与排洪建筑物，航运、农田灌溉都广泛利用了水力自控翻板闸门，并发挥了很好的效益。

本文主要研究闸门在不同倾斜角度下的水流特性及其影响因素，通过物理模型试验得出：水力自控斜轴式闸门的过闸水流流态特征、渠底及闸门上水压力的分布规律和闸门的开度规律；利用水力学相关知识推求得到水力自控斜轴式闸门的实验流量公式，并整理得到了闸门在自由出流情况下Q-H的关系；推求出水力自控斜轴式闸门的流量系数，并在综合考虑各影响因素的情况下对流量系数进行了修正。

1 模型实验

1.1 闸门模型

本文的模型实验地点设在山东农业大学水工实验室中，模型组成主要分为上游段河道、闸门段及下游段河道3部分，河道为矩形断面，宽度为400mm，如图2所示；斜轴式闸门尺寸为400mm×400mm，如图3所示。

图2 渠道

图3 斜轴式闸门

1.2 实验方案

实验方案根据闸门倾斜角度的不同共分为5大组，分别为α=30°、α=40°、α=45°、α=50°、α=60°；每大组又包括不同实验流量的6小组：Q=50m3·h-1、Q=100m3·h-1、Q=150m3·h-1、Q=200m3·h-1、Q=250m3·h-1、Q=最大实验流量(即闸门完全开启时的实验流量)，方案如表1所示。

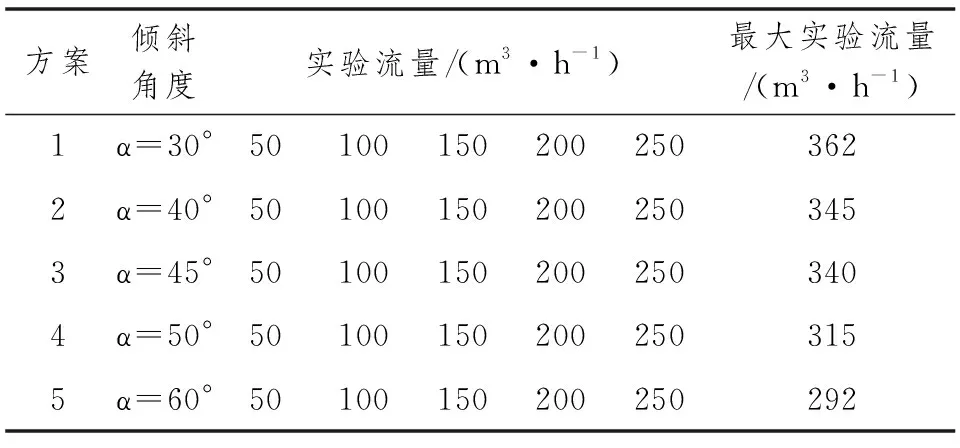
表1 斜轴式闸门实验方案表

1.3 断面设计与测量仪器

1.3.1 测量断面设计

根据实验内容，分别测定斜轴式闸门的闸前、闸后以及闸中渠道横断面的水压力，闸前与闸后的水深以及渠道的流速[4]。

本实验中，在垂直渠道水流的方向上设有15个测量横断面。渠道上共设13个水压力测量横断面，闸门上设有5个水压力测量横断面，共设有18个水压力测量断面。每个横断面设有5个测量点，从左往右依次是1～5点，断面布置如图4所示。

图4 斜轴式闸门测量断面图

1.3.2 测试仪器

实验流量测量：电磁流量计；水深测量：水位测针；流速测量：OA型-测速仪；闸门开度测量：量角器；水压力测量：测压管。

2 斜轴式闸门实验结果与分析

主要对不同角度下斜轴式闸门的实验结果进行了整合分析。

2.1 斜轴式闸门水流特性

2.1.1 斜轴式闸门的水流流态

本实验是在自由出流的情况下研究斜轴式闸门的水流特性，通过观察实验现象可得，斜轴式闸门各方案下的水流流态大致相似,即在自由出流情况下，当倾斜角度不同、实验流量相同时，倾斜角度越大，闸门的开度越大，闸前水流水面平稳，垂直于渠道轴断面，闸后水流较紊乱；当倾斜角度相同、实验流量不同时，流量越大，闸后水流越紊乱且水流流速不均，闸前水流水面平稳，垂直于渠道轴断面。当实验流量增大到最大流量时，闸前水流出现波谷，水面虽不稳，但仍垂直于渠道轴断面，闸后水流较稳定且流速较均匀。

2.1.2 斜轴式闸门过闸水流水面线

2.1.2.1 倾斜角度相同、实验流量不同的斜轴式闸门过闸水流水面线

绘制的水面线如图5所示，横坐标为断面，纵坐标为水深，cm。由图5可以看出，倾斜角度相同、实验流量不同下的过闸水流水面线大致都呈单一降落的趋势，部分地方出现壅高。在实验流量从Q=50m3·h-1增加至Q=250m3·h-1的过程中，随着实验流量增加，闸前水位逐渐增大但增幅逐渐变小；实验流量增大到最大流量后，上游出现了波谷，水流不稳定。当实验流量小于Q=150m3·h-1时，闸后水位的增幅较小；当实验流量大于Q=150m3·h-1但小于最大流量时，闸后水位增幅明显。

图5 倾斜角度相同、实验流量不同的斜轴式闸门过闸水流水面线

综上得出，在倾斜角度相同、实验流量不同的情况下，随着实验流量的增大，闸前水流的变幅逐渐减小，流态更加稳定；闸后水流的变幅逐渐增大，流态更加紊乱。

2.1.2.2 实验流量相同、倾斜角度不同的斜轴式闸门过闸水流水面线

由图6可知，在实验流量相同、倾斜角度不同的情况下，闸前与闸后水位都呈下降的趋势，且随着闸门倾斜角度的增大，闸前水深越低，闸后水深越高。

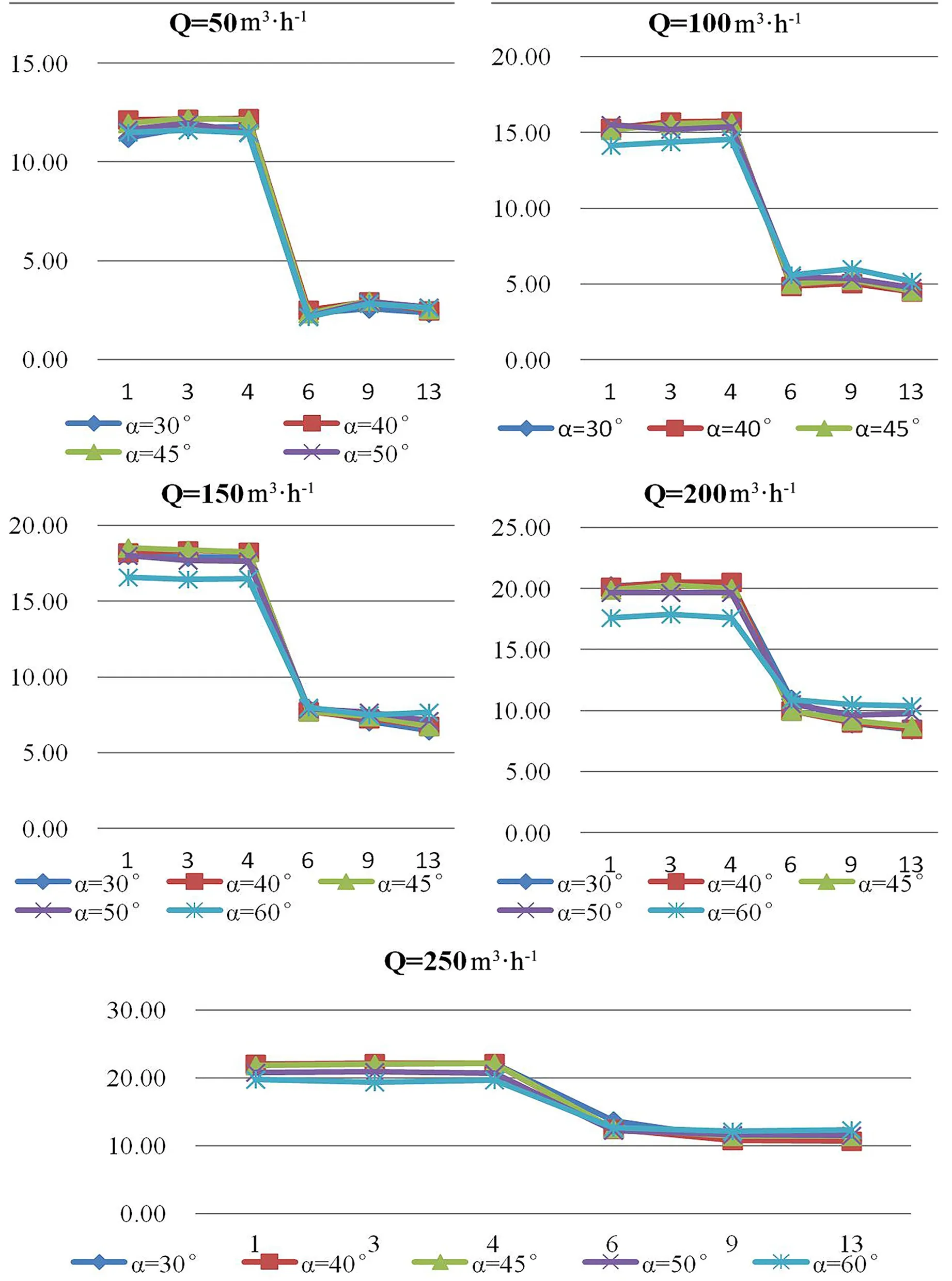
图6 实验流量相同、倾斜角度不同的斜轴式闸门过闸水流水面线

2.1.3 渠底及闸门水压力分布图

在实验的基础上，进一步研究了渠底和闸门水压力的分布规律，并绘制了水压力分布图。以α=40°的斜轴式闸门为例，渠底水压力分布图如图7所示，闸门水压力分布图如图8所示，其中断面3～11为闸后横断面，断面17～18为闸前横断面，断面12～16为闸门上的5个横断面，1～5分别为横断面上的5个测量点。横坐标代表横断面，纵坐标代表水压力，cm。

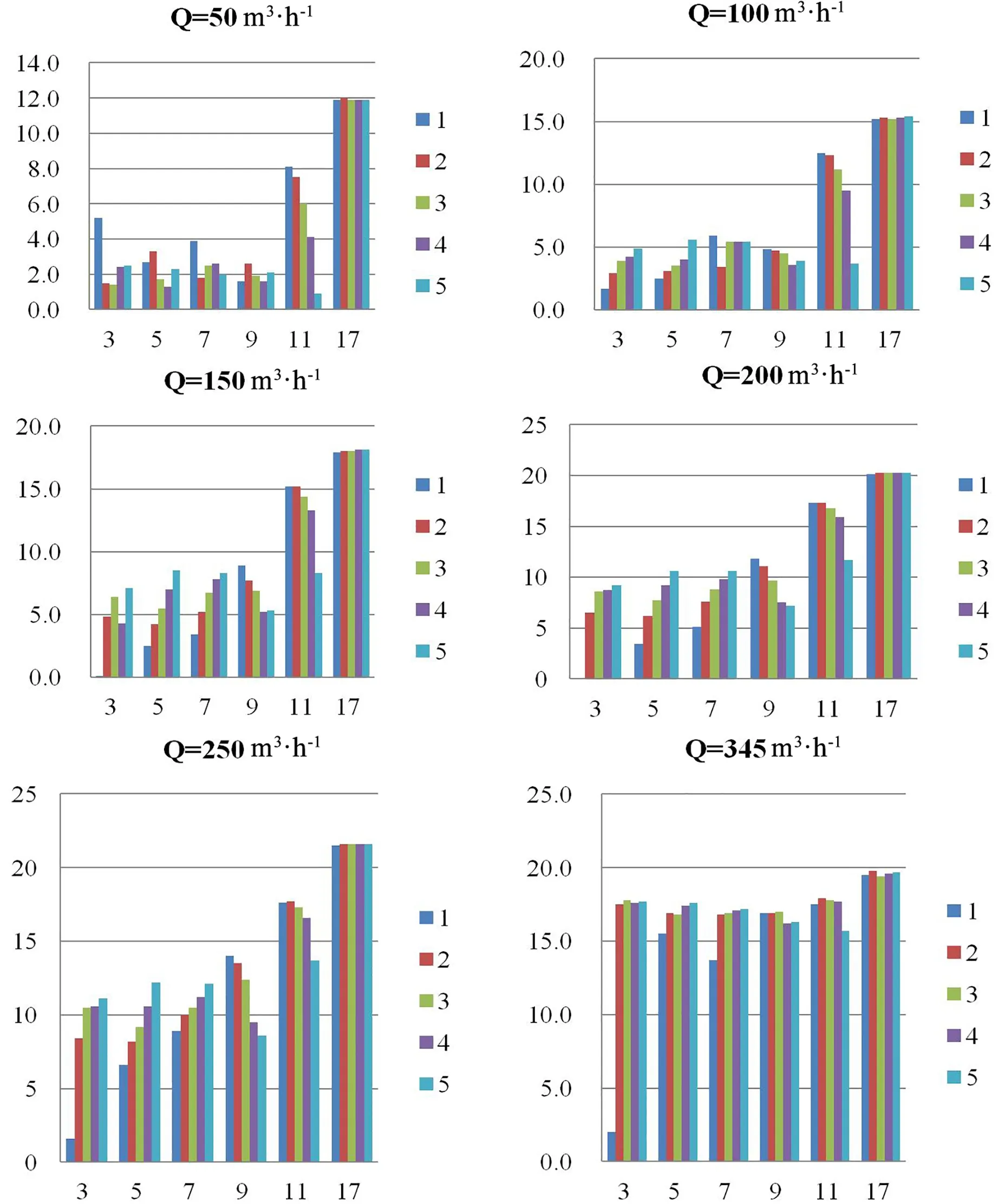
图7 渠底水压力分布

如图7所示，当闸门倾斜角度为α=40°时，不同实验流量下的闸前水压力都很稳定。当实验流量Q=50m3·h-1时，渠底水压力较小且分布不均衡，规律性不大。当实验流量从Q=100m3·h-1增加到Q=250m3·h-1的过程中，3、5和7纵断面渠底水压力从左往右逐级递增，9和11纵断面渠底水压力从左往右逐级递减(Q=100m3·h-1时的7纵断面渠底水压力与Q=150m3·h-1的3纵断面渠底水压力分布无明显规律)；当实验流量增大到最大实验流量Q=345m3·h-1时，水压力变化无明显规律，且闸前与闸后渠底的水压力差值很小。

综上得出，在倾斜角度相同的情况下，渠底水压力随着实验流量的增大而增大。

图8为闸门上水压力分布图,断面12～16是闸门从上往下的5个水压力测量断面，1～5分别是各个断面从左往右的5个测量点。当实验流量Q=50m3·h-1时,12、13、14和15断面水压力较大且变化无明显规律，16断面的水压力较大，且呈增大的趋势。随着实验流量的不断增大，水压力分布开始呈现规律性。当实验流量Q=100m3·h-1时，12和13断面水压力变小，14、15和16断面水压力增大，其上的1、2测量点水压力基本相等，3、4、5测量点水压力基本相等，且1、2测量点要小于3、4、5测量点的水压力。实验流量Q=150m3·h-1、Q=200m3·h-1、Q=250m3·h-13种情况下的水压力分布图大致相似,即12和13断面测量点水压力几乎为零；14断面水压力变化无明显规律；15和16断面水压力规律性较强，1、2测量点水压力几乎为零,3、4、5测量点水压力随流量的增大逐渐增大。当实验流量增大到最大实验流量时,12、13断面水压力几乎为零,14、15、16断面右侧3个测量点水压力且呈阶梯性增大。

综上可得，在倾斜角度相同、实验流量不同的情况下，闸门上12、13断面的水压力随实验流量的增大而减小，14断面左侧3个测量点随实验流量的增大而减小，右侧2个测量点随实验流量的增大而增大，15、16断面的水压力随实验流量的增大而增大。

2.1.4 闸门开度规律

对实验所得的数据进行整理，得到了闸门开度规律图，如图9所示。

由图9可得，在实验流量相等情况下，闸门的开度随闸门的倾斜角度的增大而增大；在闸门倾斜角度相等的情况下，闸门的开度随实验流量的增大而增大。

2.2 闸前水深H与实验流量Q的关系

对实验所得的数据进行整理，得到不同倾斜角度下闸前水深H与实验流量Q的关系图，如图10所示。横坐标为实验流量，m3·h-1，纵坐标为水深，cm。

由图10可得，在相同闸门倾斜角度的情况下，闸前水深随实验流量的增大而增大，但倾斜角度α<45°时，在实验流量Q=250m3·h-1处会形成一个“拐点”，该点之后的闸前水深会随流量的增大而降低。在相同实验流量的情况下，闸前水深随闸门倾斜角度的增加而降低。

图10 闸前水深H与实验流量Q关系

2.3 斜轴式闸门流量公式

根据《水力学》相关理论，斜轴式闸门出闸孔流的计算公式可由能量方程推求得到，并将斜轴式闸门视作宽顶堰型闸门来进行闸孔出流水力计算[5]。

对斜轴式闸门闸孔自由出流，对闸前断面0-0及收缩断面c-c应用能量方程：

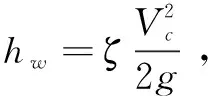
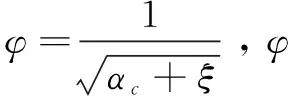
又因为Q=vcAc=vcbhc

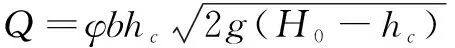
而收缩断面水深hc可表示为闸孔开度e与垂直收缩系数ε2的乘积，即hc=ε2e

令μ0=ε2φ，μ0为宽顶堰型闸孔出流的基本流量系数。则可得：

(1)

为简便计算，进一步将(1)式化简，得到：

即:

(2)

(3)

式(3)中,μ为宽顶堰型闸孔自由出流的流量系数。

2.4 斜轴式闸门的流量系数

流量系数是指某一堰闸在不同水位、不同过水断面面积上的过流能力。

2.4.1 斜轴式闸门流量系数

为计算方便，本文斜轴式闸门流量系数μ的大小可按南京水利科学研究所的经验公式计算：

(4)

2.4.2 斜轴式闸门流量系数实验结果

将实验所得数据代入公式进行计算与整理，得到不同情况下斜轴式闸门的流量系数，如表2所示。

表2 斜轴式闸门流量系数

由表2可得，在实验流量相同的情况下，斜轴式闸门的流量系数随闸门倾斜角度的增大而减小；在闸门倾斜角度相同的情况下，斜轴式闸门的流量系数随实验流量的增大而减小。

2.4.3 斜轴式闸门流量系数的影响因素

综上可得，斜轴式闸门的流量系数受闸孔入口边界条件、闸孔相对开度e/H、闸门的倾斜角度和实验流量等因素影响。

3 结论

本文通过物理模型实验结合理论分析，对斜轴式闸门的水流特性进行了实验研究，得到以下结论。

在自由出流情况下，斜轴式闸门过闸水流水面线大致呈单一降落的趋势，闸前水流流态稳定且流速分布均匀，闸后水流流态紊乱，流速分布不均；结合前辈的研究成果，利用能量方程推求得出了斜轴式闸门的流量公式，该公式适用于自由出流的情况；在斜轴式闸门流量公式的基础上推求得到了闸门的流量系数公式，并在综合考虑到流量系数各影响因素的情况下，对斜轴式闸门的流量系数进行了修正，利用式(4)进行相关计算；根据实验结果可知，斜轴式闸门的倾斜角度是影响闸门流量系数的最主要因素。