农业技术市场对农业经济增长的影响分析——基于生产函数与技术进步函数

孔祥飞

（中国社会科学院大学，北京 102400）

党的十九大报告提出要实施乡村振兴战略，加快推进我国农业农村的现代化。产业兴旺作为乡村振兴的基础，农业作为乡村的主要产业，需要通过提高乡村农业的技术含量和农业劳动生产率（黄少安，2018）[1]，不断提高农业竞争力。2021 年中央一号文件指出，加快推进农业现代化，需要打好种业翻身仗，强化现代农业科技和物质装备支撑，推进农业绿色发展，这些都离不开农业技术市场的健康发展。在我国农业由传统农业向现代农业转型过程中，农业的技术创新与发展是提高农业技术含量和农业全要素生产率的关键变量，成为农业经济增长的重要源泉。随着我国经济进入新常态和供给侧结构性改革重要阶段，技术市场在促进科技成果转化和技术进步中的作用更趋突出（杨兵和姜向荣，2017）[2]。

农业①本文中农业概念使用的为“大农业”概念，即按行业分类的农林牧副渔及相关辅助行业的定义。本文农业相关数据基于此定义范围查找，多为第一行业与各类数据中以农林牧副渔为分类依据的数据。技术市场是指在一定区域范围内，拥有各种技术商品（或技术服务行为）的供给方和具有货币支付能力的需求方进行相关农业技术商品交易的场所（李素萍，2004）[3]。农业技术市场的发育与完善在促进农业技术的创新与发展中有着极强的引导作用，进而促进农业经济增长。基于农业技术市场对农业经济增长的分析有助于理解技术市场在农业经济领域的作用程度，为我国十四五期间农业领域创新驱动发展、全面塑造发展新优势提供实证支持，为农业技术市场的发展提供合理化建议指明方向。

一、文献综述

农业技术市场的研究是农业技术研究与发展领域的重要环节，相关文献的论述主要论述全国和相关区域农业技术市场基本概况，以及基于产权角度分析的农业技术市场对农业技术进步的影响：

第一，有关全国农业技术市场的文献分析。李素萍（2004）[3]从农业技术市场存在的问题及发展的政策两个角度分析了农村技术市场的基本情况，其认为农村技术市场在发展中存在问题：市场运行机制不健全；农业技术交易的各行为主体缺乏有效的利益驱动机制，交易动力不足；农业技术市场的政策法规缺乏，市场管理规则不配套。加强农业技术市场发展的主要政策为：增加政府对农业科技的投入；大力开展组织制度创新；完善农业技术市场运行机制等[3]。黄教珍（2007）[4]重点从农业技术产权交易市场角度分析了我国农业技术市场的问题及主要对策建议，指出农业技术产权交易的健康发展助益于农业技术的创新。阮文彪（1998）[5]指出农业技术市场规范化程度低，交易秩序混乱，机会主义盛行；同时，农户技术交易风险的“外部化”机制严重缺失，加剧了技术商品有效需求的不足，这都成为了农业技术进步的重要制约因素。

第二，有关区域农业技术市场的文献分析。李稚等（1996）[6]基于“首届中国杨陵农科城技术成果博览会”交易基本情况分析的基础上，分析了西部农业科技市场的供求概况，认为目前我国农业技术变迁将呈多元取向，农业时技术的需求和吸收程度有明显提高。杨兵和姜向荣（2007）[2]重点分析了“十二五”时期山东农业技术市场的主要情况、存在问题及对策建议。陈静等（2007）[7]基于农业技术交易合同数据和企业合同登记问卷调查，研究了北京市农业技术合同交易特点和企业登记状况，从产业政策、交易平台、交易服务体系和协同机制方面提出了北京市农业技术交易促进措施。

第三，有关农业技术市场对农业技术进步的影响分析文献；王静和霍学喜（2014）[8]基于利用全国七个苹果主产省苹果种植户实地调查数据，构建基于农户要素稀缺诱致性技术选择的效用模型，并将此模型转换为实证分析模型，其研究发现：生产要素价格相对变动是诱致农户技术选择产生偏向的关键市场信号，而农业技术市场发育相对滞后，技术交易成本成为制约农户要素稀缺诱致性技术选择行为的关键因素。李宪宝等（2010）[9]重点分析了农业技术交易对象中非实体性要素交易未完成所造成的产权残缺现象，通过数理模型分析，得出产权残缺降低了农户均衡收益、影响力农机推广的效果的结论。

综上所述，既有大部分文献停留在农业技术市场的基本的描述性分析，小部分分析了农业技术市场对农业技术进步的影响分析，但都未对农业技术市场对农业经济增长的最终联系与影响进行研究，这与中国新形势下稳定粮食产量、保障粮食安全的国家要求并不相符。农业技术市场对农业经济增长的影响程度分析应是农业技术市场领域研究中应该首先解决的问题，近年的相关研究也止步于农业技术市场对农业技术进步的分析，主要是基于农业技术市场某一具体问题的分析，宏观上的整体把握需要研究实证加以解决。本文将基于生产函数与技术进步函数，运用间接方法，通过对农业经济增长中农业技术市场的贡献程度研究，运用实证分析来充分认识农业技术市场对农业经济增长的影响。

二、农业技术市场对农业经济增长影响分析方法①本文研究方法参考沈利生2010 年未发表报告中相关研究方法，故无法进行具体的文献引用。

某一变量对另一变量增长的贡献的研究主要集中于生产要素对经济增长的贡献领域，其中较多的是科技投入对经济增长的贡献研究，其主要涉及两种研究方法：第一种是直接建立经济增长与科技投入关系的模型；第二种是建立起扩展的生产函数，将科技投入、资本投入与劳动投入作为共同的投入要素，进而计算出科技投入对经济增长的贡献。以上方法存在忽视重要解释变量和变量间共线性问题，为此，本文结合以上既有两种方法及本文研究内容，基于农业技术市场通过影响全要素生产率，再影响农业总产出的逻辑，测算农业技术市场对农业总产出的影响，逻辑与经济含义上具有合理性。

结合本文研究，其测算过程为：首先，建立通常的生产函数，把第一产业产出（GDP）作为被解释变量，将固定资产投资与就业人数作为投入要素，利用生产函数测算出全要素生产率（TFP）；其次，通过生产函数分别测算出全要素生产率（TFP）、固定资产投资与就业人数对农业经济增长的贡献；再次，将全要素生产率作为一个新的被解释变量，将农业技术市场交易额作为被解释变量，建立一个技术进步函数模型；最后，通过对新的函数模型进行分析，测算出农业技术市场交易额对全要素生产率的贡献，与全要素生产率对农业经济增长贡献相乘得到农业技术市场对农业经济增长的贡献。

三、农业技术市场对农业经济增长影响的实证分析

（一）数据说明

本文数据类型主要为第一产业现价GDP、第一产业固定资产投资、第一产业就业人数、全国技术市场成交合同额（按社会经济目标分：农林牧副渔业发展），分别记为GDP、GDZCTZ、L、HTJE。本文以农产品生产者价格指数将第一产业GDP 处理为基于2006 年不变价的真实GDP，记为RGDP，以固定资产投资价格指数将第一产业固定资产投资处理为基于2006 年不变价的真实固定资产投资，记为RGDZCTZ。本文以农业生产资料价格分类指数（按农业生产服务分类）将HTJE处理为基于2006 年不变价的真实全国技术市场成交合同额，记为RHTJE。由于缺乏全国技术市场成交合同额及可借用的价格指数数据，本文以农业生产资料价格分类指数（按农业生产服务分类）替代。本文相关数据如表1 所示。

表1 2006—2019 年GDP、GDZCTZ、L、HTJE、RGDP、RGDZCTZ 及RHTJE 数据

（二）农业生产函数和全要素生产率对农业经济增长的贡献

1.农业生产函数模型

结合本文研究，在“希克斯中性”技术进步的假设下，考虑技术进步的柯布—道格拉斯农业生产函数为：

其中：RGDPt是第一产业历年经济产出（即GDP，2006 年不变价）；At是全要素生产率（TFP），A0是基年的TFP值；γ是TFP的增长率；RGDZCTZt是第一产业历年固定资产投资，以2006 年不变价表示；Lt第一产业历年就业人数；α和β分别为RGDP 和L的产出弹性，且α+β=1。

则可得全要素生产率At的计算公式如下：

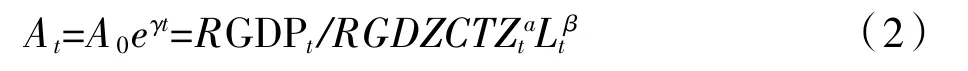
在实际估计生产函数时被解释变量为劳均产出（RGDP/L），解释变量是劳均固定资产投资（RGDZCTZ/L）和时间趋势T，并取对数，即生产函数形式为：

式（3）可改写为：

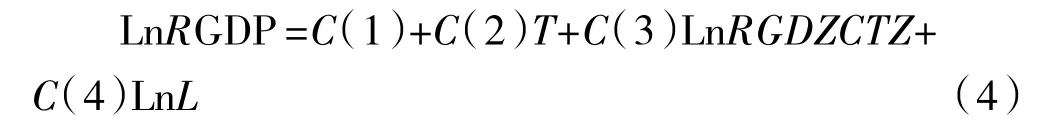
其中：C（3）=α，C（4）=β，C（3）+C（4）=1。

2.农业生产函数模型的实证分析

（1）Eviews 回归结果分析。经过Eviews 处理，Ln（RGDP/L）、c、T、Ln（RGDZCTZ/L）的回归结果如下：

通过回归结果分析，R2可决系数很高，说明回归方程的解释程度很高。F统计值很高，说明回归方程的整体性回归效果较好。通过查询德宾—沃森d统计量表，在5%显著性水平上，n=14，k（不包括常数项的解释变量个数）=2，查表得dL=0.905，dU=1.551，dL＜D.W.=1.105＜dU，则不能确定模型随机项是否存在序列自相关。需注意，本模型趋势项T 解释变量在5%显著水平下，不拒绝原假设，这说明模型本身可能不存在长期趋势变动，对于寻找Ln（RGDP/L）、Ln（RGDZCTZ/L）的长期均衡关系影响不大，不影响模型本身对于本研究的使用。

（2）模型变量序列自相关的Correlogram-Qstatistice 检验、Breush-Godfrey LM 检验。通过Eviews对模型进行Correlogram-Q-statistice 检验，输出结果为：

由图1 可知，Eviews 软件默认系统滞后阶数为12，自相关系数AC与偏自相关系数PAC各滞后阶数内都在零值附近徘徊，数值较小，都位于两虚线之内，说明模型不存在序列自相关；同时，Q统计量的P值在5%显著水平下，各阶数均接受不存在序列相关的原假设。综上所述，模型不存在序列自相关。

图1 生产函数模型Correlogram-Q-statistice 检验输出结果

通过Eviews 对模型进行Breush-Godfrey LM 检验，输出结果为：

由图2 可知，Eviews 软件通过相关信息准则默认残差项滞后阶数为2，LM 检验在5%显著水平下，P值较大，接受不存在序列自相关的原假设。综上所述，通过D.W.值、自相关系数、偏自相关系数、Q 统计量、Breush-Godfrey LM 检验的分析，可以确定农业生产函数模型不存在时间序列自相关，模型本身不需要进行序列自相关修正。

图2 生产函数模型Breush-Godfrey LM 检验输出结果

（3）模型变量序列平稳性的ADF检验。进行协整分析以前，我们必须先检验变量是否是平稳的。因为只有在它们是同阶单整时，才可能存在协整关系。我们采用Dickey-Fuller 的ADF检验方法，检验过程如下：

①对时序变量Ln（RGDZCTZ/L）进行单位根检验：经过试验，使检验方程中的SIC值最小的滞后期最大为2，Eviews 单位根检验结果如下：

由图3 可知，当模型中含有趋势项和常数项时，其P值分别为0.040 3、0.038 8，在5%显著性水平下，拒绝不存在趋势性与常数项的原假设，故Ln（RGDZCTZ/L）单位根检验输出结果如表2 所示。

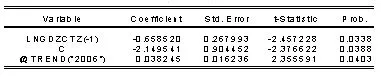
图3 序列Ln（RGDZCTZ/L）单位根检验结果中趋势项与常数项回归结果

表2 序列Ln（RGDZCTZ/L）单位根检验结果

由表2 可知，当模型中含有常数项和趋势项时，统计量ADF=-2.457228，在置信水平为0.01、0.05和0.1 下，临界值分别为-4.886 426、-3.829 975 和-3.362 984，显然也有统计量大于临界值，因此我们需要进行一阶差分处理。

②令序列Ln（RGDZCTZ/L）的一阶差分序列为吟Ln（RGDZCTZ/L），对该序列进行单位根检验，检验结果如下。

由表3 可知，当模型中含有常数项和趋势项时，统计量ADF=-3.532603，在置信水平为0.01、0.05和0.1 下，临界值分别为-5.124 875、-3.933 364 和-3.420 030，显然在1%、5%显著水平下，有统计量大于临界值，接受存在单位根的原假设；当模型中仅含有常数项，同理，在5%显著水平下，有统计量小于临界值，不接受存在单位根的原假设，故序列变量△Ln（RGDZCTZ/L）平稳，Ln（RGDZCTZ/L）一阶单整，即I（1）。

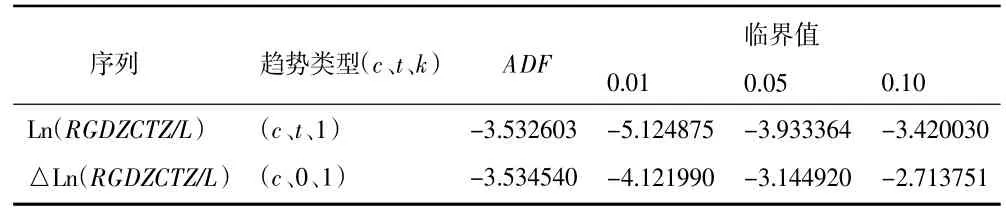
表3 序列△Ln（RGDZCTZ/L）单位根检验结果

需注意，当模型中含有常数项和趋势项时，趋势项P值为0.866 3，在5%显著水平下接受不存在趋势项的原假设；当模型中仅含有常数项时，常数项P值为0.011 6，在5%显著水平下，拒绝不存在常数项的原假设。本文从此处，无特殊情况，将不在陈述。

③对时序变量Ln（RGDP/L）进行单位根检验：经过试验，使检验方程中的SIC值最小的滞后期最大为2，Eviews 单位根检验结果如下。

由表4 可知，当模型中含有常数项和趋势项时，统计量ADF=-2.308874，在置信水平为0.01、0.05和0.1 下，临界值分别为-4.886 426、-3.828 975 和-3.362 984，显然有统计量大于临界值，接受存在单位根的原假设；当模型中仅含有常数项，同理，显然有统计量大于临界值，接受存在单位根的原假设；当模型中只有滞后项时，同理，显然有统计量大于临界值，接受存在单位根的原假设。综上所述，序列变量非平稳，需要对变量Ln（RGDP/L）进行一阶差分单位根检验。

表4 序列Ln（RGDP/L）单位根检验结果

④令序列Ln（RGDP/L）的一阶差分序列为△Ln（RGDP/L），对该序列进行单位根检验，检验结果如表5 所示。

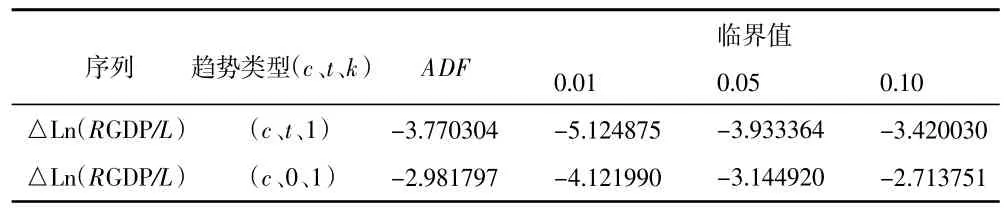
表5 序列△Ln（RGDP/L）单位根检验结果

由表5 可知，当模型中含有常数项和趋势项时，统计量ADF=-3.770304，在置信水平为0.01、0.05下，临界值分别为-5.124 875、-3.933 364，显然在1%、5%显著水平下，有统计量大于临界值，接受存在单位根的原假设；当模型中仅含有常数项，同理，在10%显著水平下，有统计量小于临界值，不接受存在单位根的原假设，故序列变量△Ln（RGDP/L）平稳，Ln（RGDP/L）一阶单整，即I（1）。

如图4 所示，当模型中仅含有常数项时，常数项对应P值为0.048 3，在5%显著性水平下，拒绝不存在常数项的原假设，这与表5 中，ADF统计量在5%显著水平下，接受存在单位根的原假设矛盾，这时一般可降低ADF统计量标准，看是否仍然矛盾，在10%显著水平下，模型拒绝存在单位根的原假设，故Ln（RGDP/L）可一阶单整，即I（1）。

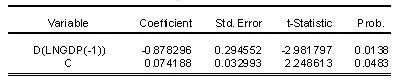
图4 序列Ln（RGDP/L）单位根检验结果中常数项回归结果

（4）模型序列协整关系的ADF检验。农业生产函数模型回归结果为二元回归结果，其中一元为T趋势变量，由于此变量为等差为1 的等差数列，为线性趋势，故其本身T可分别视为平稳数列和一阶单整数列，即T-I（1）。

由于Ln（RGDZCTZ/L）、T、Ln（RGDP/L）都为一阶单整数列，故模型可以进行协整检验，本协整检验对残差项仍进行ADF检验，基于SIC准则，检验最大滞后阶数为2，检验结果如下：

由表6 可知，当模型中含有常数项和趋势项时，统计量ADF=-2.222350，在置信水平为0.01、0.05和0.1 下，临界值分别为-4.992 279、-3.875 302 和-3.388 330，显然有统计量大于临界值，接受存在单位根的原假设；当模型中仅含有常数项，同理，显然有统计量大于临界值，接受存在单位根的原假设；当模型中只有滞后项时，同理，显然在5%显著水平下，其统计量小于临界值，拒绝存在单位根的原假设。综上所述，模型残差为平稳时间序列，故协整关系通过检验，则可以得出农业生产函数模型的回归项存在长期均衡关系，在长期分析中，可以使用原回归结果，回归结果显示a=2.1242、β=-1.1242。

表6 模型基于残差（R）的协整检验结果

3.全要素生产率对农业经济增长的贡献

结合以上分析，通过公式（2）可求得农业生产的全要素生产率TFP，结果如表8 所示。对对数线性农业生产函数LnRGDP=LnA+aLnRGDZCTZ+βLnL求全微分：

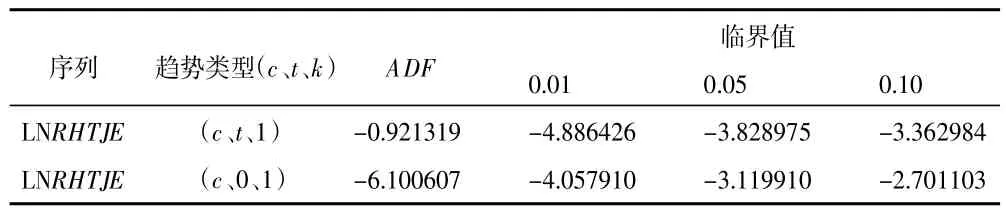
表8 序列LNRHTJE 单位根检验结果

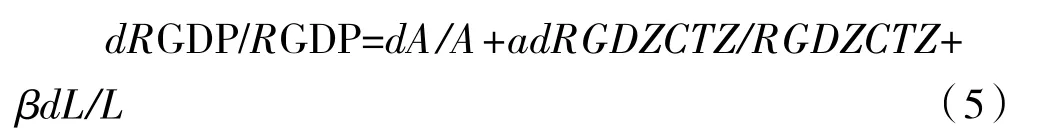
对公式（5）微分形式转化为差分形式得：

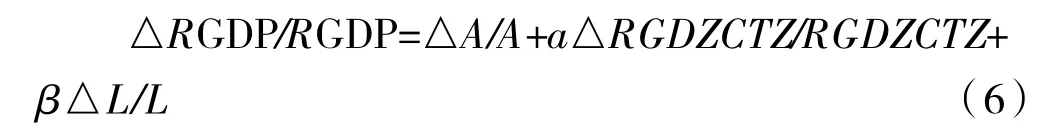
公式（6）可进一步转化为：

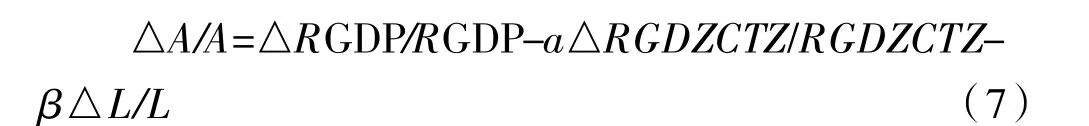
用相应小写表示增长率，可得：

两边同时除于rgdp可得农业的全要素生产率对农业经济增长的贡献公式：

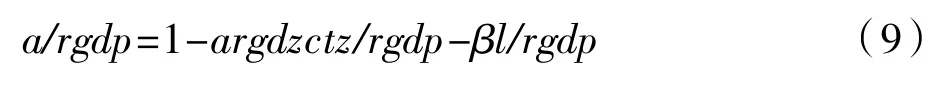
公式（9）中argdzctz/rgdp和βl/rgdp分别是固定资产投资和农业就业人数对农业经济增长的贡献。结合回归结果和相应公式，计算结果如表7 所示。

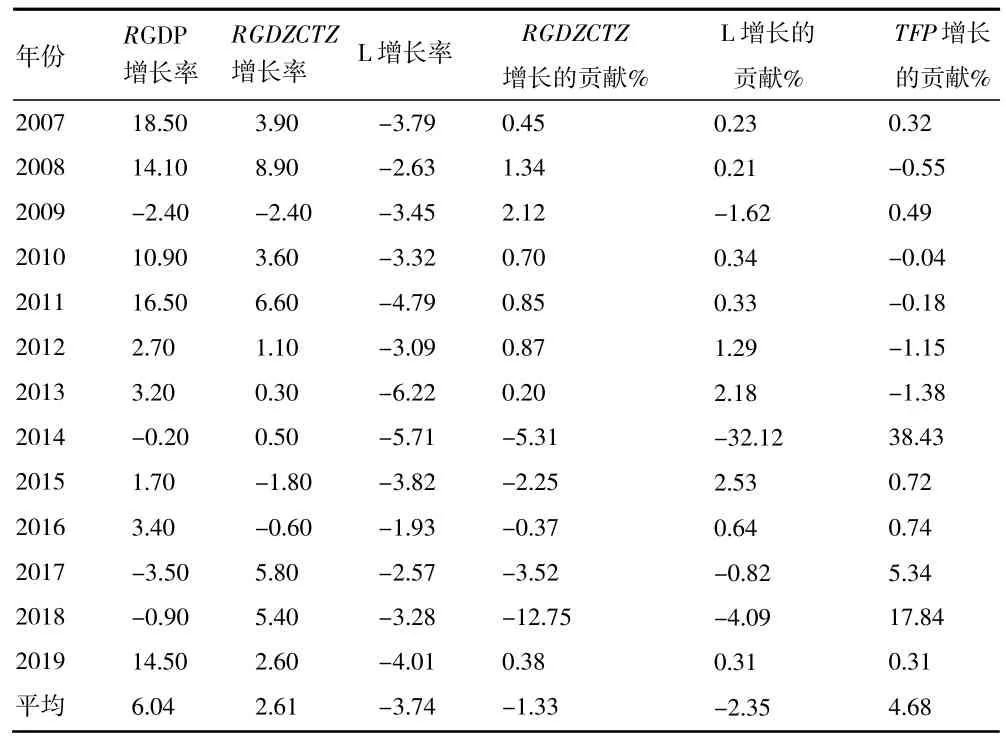
表7 2007—2019 年固定资产投资、农业就业人数、全要素生产率对农业经济增长的贡献

（三）农业技术进步函数与农业技术市场合同金额对全要素生产率的贡献

1.农业技术进步函数及相关公式

本文中农业技术进步函数考虑使用指数化函数模式，使用非线性模式更接近于现实，其具体形式如下：

其中：TFPt是农业生产函数计算数值；At是除农业技术市场合同金额外的其余影响因素的效率数值，A0是其基年值；γ是At的增长率；RHTJE是农业技术市场按农林牧副渔分类的合同金额，以2006年不变价表示；其中，α为RHTJE的弹性。

由于农业技术进步函数与农业生产函相关公式推导过程一致，故省略。下文实证分析中所需公式如下：

公式（9）中arhtje/tfp是农业技术市场合同金额对农业全要素生产率增长的贡献。

2.农业技术进步函数模型的实证分析

（1）农业技术进步函数的Eviews 初步回归结果。经过Eviews 处理，LnTFP、C、T、LnRHTJE的回归结果如下：

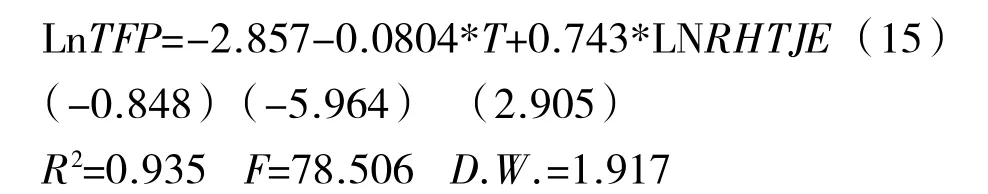
通过回归结果分析，R2可决系数很高，说明回归方程的解释程度很高。F统计值很高，说明回归方程的整体性回归效果较好。通过查询德宾—沃森d统计量表，在5%显著性水平上，n=14，k（不包括常数项的解释变量个数）=2，查表得dL=0.905，dU=1.551，dU＜D.W.=1.917＜4-dU，可判断模型随机项不存在序列自相关。需注意，本模型常数项解释变量在5%显著水平下，不拒绝原假设，这说明模型本身可能过原点，对于寻找LnTFP、LnRHTJE的长期均衡关系影响不大，不影响模型本身对于本研究的使用。

（2）模型变量序列自相关的Correlogram-Qstatistice检验、Breush-Godfrey LM 检验。通过Eviews对模型进行Correlogram-Q-statistice 检验，输出结果为：

由图5 可知，Eviews 软件默认系统滞后阶数为12，自相关系数AC与偏自相关系数PAC大部分滞后阶数内都在零值附近徘徊，数值较小，都位于两虚线之内，但滞后阶数为2 时，其自相关系数AC与偏自相关系数PAC较大，位于两条虚线外，说明模型可能存在二阶序列自相关；同时，Q统计量的P值在5%显著水平下，除二阶滞后阶数外，其余滞后阶数均接受不存在序列相关的原假设。综上所述，模型可能存在滞后阶数仅为二阶的序列自相关。

图5 农业技术进步函数模型Correlogram-Q-statistice检验输出结果

通过Eviews 对模型进行Breush-Godfrey LM 检验，输出结果为：

由图6 可知，Eviews 软件通过相关信息准则默认残差项之后阶数为2，LM 检验在5%显著水平下，P值较小，拒绝不存在序列自相关的原假设。综上所述，通过D.W.值、自相关系数、偏自相关系数、Q 统计量、Breush-Godfrey LM 检验的分析，可以确定农业生产函数模型存在二阶时间序列自相关，模型本身需要进行序列自相关修正。

图6 农业技术进步函数模型Breush-Godfrey LM 检验输出结果

（3）模型变量序列自相关的AR（p）模型修正。通过Eviews 对模型进行AR（p）模型的自相关修正处理，其输出结果为：

由AR（2）模型回归结果可知，R2可决系数很高，说明回归方程的解释程度很高。F统计值很高，说明回归方程的整体性回归效果较好。通过查询德宾—沃森d统计量表，在5%显著性水平上，n=14，k（不包括常数项的解释变量个数）=3，查表得dL=0.767，dU=1.779，dU＜D.W.=1.968＜4-dU，可判断模型随机项不存在序列自相关。需注意，本模型常数项解释变量在5%显著水平下，不拒绝原假设，这说明模型本身可能过原点，对于寻找LnTFP、LnRHTJE的长期均衡关系影响不大，不影响模型本身对于本研究的使用。

农业技术进步函数通过AR（2）模型自相关修正后，需对修正后模型的自相关性进行重新检验，Eviews 软件对模型进行Correlogram-Q-statistice 检验，输出结果为：

由图7 可知，Eviews 软件默认系统滞后阶数为12，自相关系数AC与偏自相关系数PAC滞后阶数内全部都在零值附近徘徊，数值较小，都位于两虚线之内，说明模型不存在序列自相关；同时，Q统计量的P值在5%显著水平下，滞后阶数均接受不存在序列相关的原假设。综上所述，农业技术进步函数经过AR（2）自相关修正后，不存在序列自相关。

图7 农业技术进步函数自相关修正后Correlogram-Q-statistice 检验输出结果

（4）农业技术进步函数模型变量的时间序列平稳性检验。进行协整分析以前，我们必须先检验变量是否是平稳的。因为只有在它们是同阶单整时，才可能存在协整关系。我们采用Dickey-Fuller 的ADF检验方法，检验过程如下：

①对时序变量LnRHTJE进行单位根检验：经过试验，使检验方程中的SIC值最小的滞后期最大为2，Eviews 单位根检验结果如下：

由表8 可知，当模型中含有常数项和趋势项时，统计量ADF=-0.921319，在置信水平为0.01、0.05 和0.1 下，临界值分别为-4.886 426、-3.828 975 和-3.362 984，显然有统计量大于临界值，接受存在单位根的原假设；当模型中仅含有常数项，同理，显然有统计量小于临界值，拒绝存在单位根的原假设。综上所述，序列变量平稳，故变量LnRHTJE无滞后阶数，即LnRHTJE-I（0）。

②对时序变量LnTFP进行单位根检验：经过试验，使检验方程中的SIC值最小的滞后期最大为2，Eviews 单位根检验结果如下：

由表9 可知，当模型中含有常数项和趋势项时，统计量ADF=-2.215204，在置信水平为0.01、0.05和0.1 下，临界值分别为-4.992 279、-3.875 302 和-3.388 330，显然有统计量大于临界值，不拒绝存在单位根的原假设；当模型中仅含常数项时，统计量大于临界值，不拒绝存在单位根的原假设；当模型中无趋势项与常数项时，在5%显著水平下，拒绝存在单位根的原假设。综上所述，序列变量平稳，故变量LnTFP无滞后阶数，即LnTFP-I（0）。

表9 序列LnTFP 单位根检验结果

由于LnRHTJE-I（0）、LnTFP-I（0），两变量均为平稳性时间序列，所以农业进步函数经AR（2）自相关修正后的结果无需进行协整关系检验，此回归结果证明了LnRHTJE、LnTFP存在长期均衡关系，在长时期，Eviews 回归结果公式（16）可以使用，此时a=0.718。

3.农业技术市场合同金额对全要素生产率的贡献。通过arhtje/tfp表达式，结合Eviews 输出结果，可求出农业技术市场合同金额对全要素生产率的贡献，其计算结果如表10 所示。

表10 2007—2019 年农业技术市场合同金额对全要素生产率的贡献

四、农业技术市场对农业经济增长影响分析

农业技术市场合同交易额是农业技术市场发展的关键表示性指标，农业技术市场对农业经济增长的贡献可以很好地表示农业技术市场对农业经济增长的影响程度。结合本文，我们将全要素生产率对农业经济增长的贡献值与农业技术市场合同交易额对全要素生产率的贡献值相乘，可以得到农业技术市场合同交易额对农业经济增长的贡献值，结合本文相关计算数值，其计算结果如表11 所示。

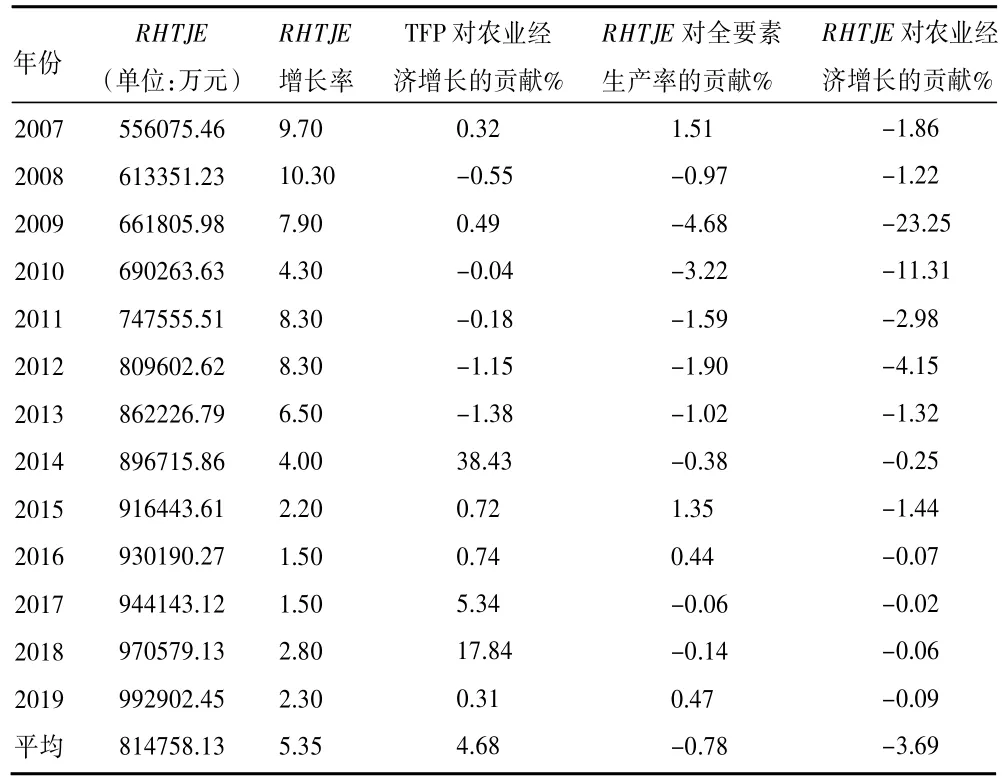
表11 农业技术市场交易合同金额对农业经济增长的贡献

结合本文实证分析结果，结合表7、表10 及表11，主要结论如下：

第一，我国农业TFP增长率总体呈下降趋势。自2007 年以来，我国农业TFP年平均增长率为-3.73%。这同我国农业机械化水平不断提高，农业结构由传统农业向现代农业转型的发展趋势不相一致，尤其是在个别年份出现了严重的农业TFP增长率大幅下降的现象。这表明，在当前我国“大国小农”的农情下，提高农业TFP增长率的增长，不仅依赖于我国农业技术的创新和市场化的建设，而且需要其他相应举措，例如配套制度改革与创新，实现我国农业各要素综合生产能力的提升。第二，农业TFP对农业经济增长的贡献总体较小，且变动较大。自2007 年以来，我国农业TFP对农业经济增长的年平均贡献程度为4.68%。这表明，我国农业TFP对农业经济增长的贡献仍然偏低。这一方面受制于我国农业科技水平；另一方面则缺乏相应的支持农业技术转化的相应的配套政策，加之我国小农户在我国农业经营中占据主体地位，如何将小农户引入现代农业的发展进程，将先进的农业技术、管理水平、优质的种质资源向小农户推广与应用，仍面临许多困难。正是由于这些困难的存在，在一定程度上限制了农业的发展，不利于农业TFP的提升，从而也就导致农业TFP对农业经济增长的贡献总体较小。第三，农业技术市场合同金额对农业TFP几乎无影响，这并不是否定农业技术对农业增长无影响，这与我国农业技术市场的交易结构、产权保护程度、技术推广体制有强相关性，现有农业技术市场交易架构可能多为劳动密集型与资产密集型技术，产权保护的缺失，使得关键性农业技术趋向于半公共品性质，技术推广效率低下，这些都使得农业技术对农业经济增长的作用未通过农业技术市场发挥出来。第四，农业技术市场效率低下，自2007 年以来，农业技术市场不变价合同交易总额年平均增长5.35%，而农业技术市场合同金额对农业TFP几乎无影响，市场效益来源于规模与效率两个方面，农业技术市场的技术转化效率并不能满足农业经济增长的需要，现有农业技术市场交易类型以我国农业领域要素市场比较优势为引导，技术密集型产品开发不足。第五，我国现有农业技术市场有待于进一步完善。自2007 年以来，我国农业技术市场合同金额对农业经济增长的年平均贡献为-3.69%，但自2009 年以来，逐渐转正。说明我国农业技术市场经过不断发展，逐渐适应于我国农业现代化与乡村振兴的需要。但是农业技术市场的技术领域的转化与中介作用发挥仍不足，农业技术市场在农业领域的相对落后，成为我国农业技术促进农业健康发展的重要瓶颈。

五、针对农业技术市场健康发展的建议

根据本文的相关结论，结合我国农业现代化发展中面临的问题与挑战，主要从以下五个方面提出相应的对策建议，以期促进农业技术市场的健康发展和农业现代化水平的提升。

第一，深化农村改革，完善农业农村现代化的制度建设。以深化农村土地制度改革为突破点，推进农业现代化转型，为农业技术在农村的推广与应用、农业全要素生产率的提高营造良好的制度环境。积极探索小农户与现代农业的有机衔接方式，积极推进农业技术的需求主体在稳固现有新型农业经营主体和服务主体的同时，兼容普通农户、小农户的市场技术需求，不断拓展农业技术的市场空间。

第二，持续推进农业技术创新。在农村推进乡村振兴的背景下，积极探索适应当前农户需求的农业技术，发展适宜我国农业生产要素比较优势的技术类型，不断提高农业技术的适用性。同时，结合我国农业向现代农业转型的发展趋势，积极探索适应未来农业发展方向的农业技术，推进农业的现代化、集约化、生态化、智能化发展。与此同时，不断增加农业技术人才的培养，财政资金的支持，关键核心技术的攻关，农业种质资源的开发利用与保护，不断增强我国农业技术的竞争力。

第三，完善农业技术交易市场，加强农业技术的产权保护。产权清晰是市场高效运行的必要条件，加强农业技术市场的制度体系建设，推进农业技术市场交易的法制化、规范化，加强知识产权保护，增加科研人员的收益比重。

第四，培育新型农业经营主体。现代化农业的发展离不开新型农业经营主体的培育，通过培育龙头型公司化农业企业、家庭农场经营、农业托管服务公司等新型农业经营主体，能够为农业技术在农业领域的应用创造条件，因为同小农户相比，新型农业经营主体更有能力、意愿去尝试新鲜事物，接受农业技术创新的成果，更有利于农业技术市场交易行为的发生。

第五，完善农业技术推广体系，实现农业技术的转化与应用。农业技术推广体系有助于技术供需双方实现有效衔接，农业技术的需求主体不仅包括新型农业经营主体，而且也包括广大的普通农户。农业技术在基层的推广过程中要注重引导，鼓励试验，从而为农业技术开拓农村市场创造条件。