基于多尺度时域平均分解和模糊熵的船用风机故障诊断方法
2022-05-31蒋佳炜胡以怀方云虎芮晓松
蒋佳炜 胡以怀 方云虎 张 陈 芮晓松 汪 猛
上海海事大学商船学院,上海,201306
0 引言
近年来随着计算机技术与智能算法的发展,机械设备的故障诊断方法也在向智能化方向发展[1]。在机械设备故障诊断中,机械振动信号对机器故障的敏感性远高于温度和压力等参数对机器故障的敏感性[2]。船舶旋转机械通常在多种振源的环境中运转,其振动信号大多包含多种非线性、非平稳噪声,对其进行故障诊断时仅使用以傅里叶变换为基础的频谱分析有较大的局限性[3]。如何对信号进行降噪、提取有效的故障信息、进行故障模式识别一直是国内外学者的研究热点[4-5]。为了在时频域更好地解析信号的特征,相关学者定义并使用了短时傅里叶变换(short-time Fourier transform,STFT)、小波变换[6]、希尔伯特黄变换(Hilbert Huang transform,HHT)等方法[7-8]。
STFT需要选择合适的窗函数进行分解,分辨率的选择对结果影响较大。小波变换需要选择基函数,小波基函数构造不准确就难以产生理想的结果。HHT主要包括经验模态分解(empirical mode decomposition,EMD)和Hilbert-Huang变换,可以将信号分解成多个具有物理意义的模态本征函数,但是存在模态混叠和端点效应等问题。变分模态分解(variational mode decomposition,VMD)是基于维纳滤波、希尔伯特变换分解信号的自适应方法,在故障诊断领域的应用取得了一定成果[9],但该方法需要预先判断信号中含有的模态个数并预设惩罚因子,不同的预设参数对结果影响较大,并且应用于电机故障诊断时无法直接分解其回转频率及倍频附近频段的信号。在船舶机舱这样较为复杂的环境中,若在故障信号频率附近存在其他变频干扰信号则会对其模态造成很大的影响,且EMD与VMD都存在端点效应,这也是模态分解方法的不足之一。
船舶旋转机械的故障信息往往集中在转速的倍频附近,McFADDEN[10]提出的时域平均法(time domain averaging)或称时域同步平均法(time synchronous averaging,TSA)的本质恰好是一系列等距分布的带通滤波器,该方法可以有效抑制其他频率下的噪声,但存在一些不足,使得其在故障诊断领域并未得到广泛应用。为此,学者们也提出了许多改进方法。刘红星等[11]提出了一种新算法,该算法解决了周期截断误差对平均结果的影响问题。HALIM等[12]将TSA方法与小波分析方法结合起来,提取出振动信号中的波形特征,该方法对时域平均法在故障诊断领域的运用有积极的影响。McFADDEN等[13]提出了一种基于相位补偿的TSA方法,通过对每段截取信号进行相位补偿来消除非整数倍周期截断,该方法提高了TSA法的性能。MARK[14]、AHAMED等[15]对TSA方法进行了改进,并在啮合齿轮振动信号分析应用方面取得了一定的成果。冯武卫等[16]提出了采用FIR多带滤波器实现时域同步平均功能的方法,该方法提高了时域平均法在实际工程中的应用性。
综上,国内外学者均从不同方面改进或提高了时域平均分析方法的效果,并在一定程度上避免了该方法的局限性,但仍存在以下问题:①时域平均方法将特定频率下的倍频信号波形混叠起来,难以分解;②对信号进行时域平均处理后只能获取特定频率的信息,无法一次性地提取全频域内的故障特征信息;③需要采集特定的键相信号。虽然随着传感器技术的发展,在船舶机舱这样复杂、条件恶劣的环境中也可以获取键相信号,但是获取时往往存在一定困难[16],并且需要键相信号,这在一定程度上限制了TSA方法的使用。
笔者受到信号模态分解方法的启发,针对TSA方法存在的问题以及EMD与VMD无法指定分解特定频段信号和模态信号且易受频域相近的噪声信号干扰的问题,提出了多尺度时域平均分解法(multiscale time-domain averaging decomposition,MTAD)方法,通过仿真信号分析和故障模拟试验数据分析来证明所提方法的有效性。
1 多尺度时域平均分解法
对于一个有限长的含周期信号和其他信号且均值为零的振动信号y(t),假设它满足狄利克雷条件,则y(t)可以看成如下形式的信号:
y(t)=e(t)+g(t)
(1)
式中,g(t)为周期信号;e(t)为其他信号。
设周期信号g(t)的周期为T,将其分割成N段长度为T的时间序列片段。设g(t)中第n段时间序列为Pn(φ),根据周期函数定义,有
Pn(φ)=P(n+1)(φ)
(2)
式中,n=1,2,…,N;相位φ∈[0,T)。
将y(t)以周期T分割成N段长度相等的时间序列片段后,设Yn(φ)为y(t)中第n段序列片段,则可以将Yn(φ)看作是由Pn(φ)和其他信号e(t)分割后的第n段序列片段en(φ)组成:
Yn(φ)=Pn(φ)+en(φ)
(3)

(4)
1.1 时域同步平均法(TSA)
基于上述振动信号y(t)的特性,其时域同步平均算法可以概括为y(t)与特定周期下的周期信号g(t)的卷积[10]:
(5)
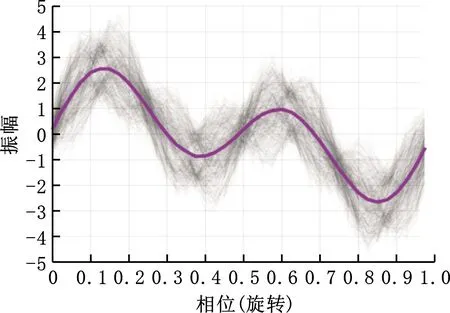
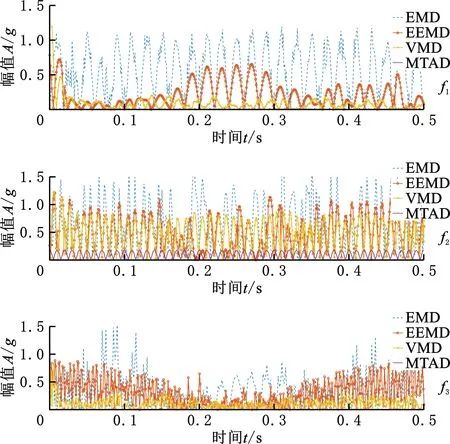
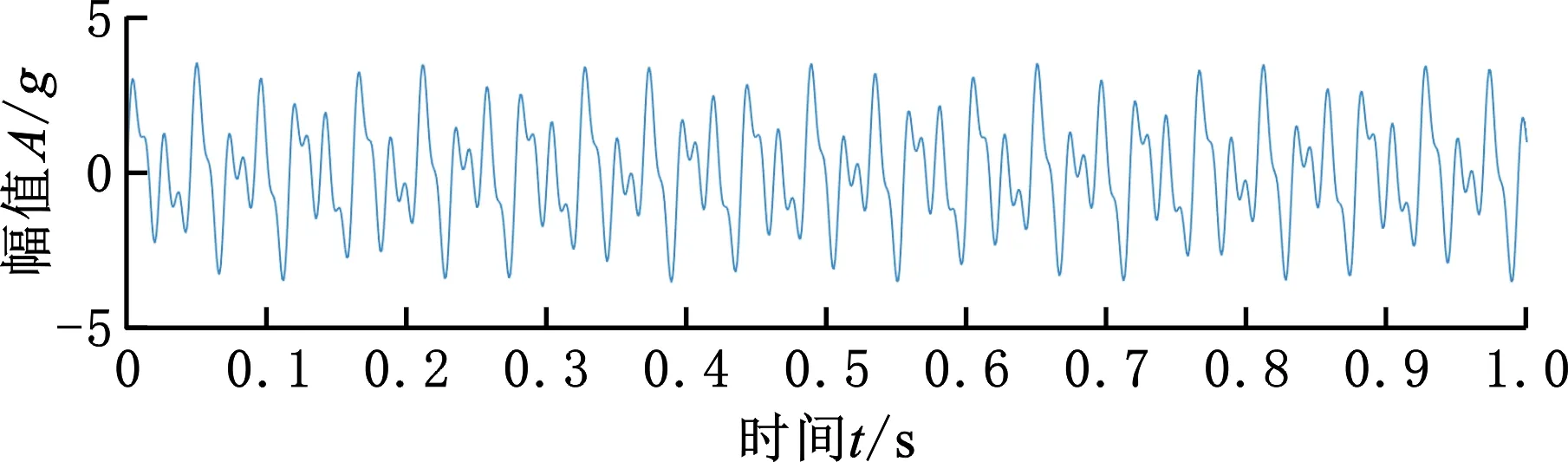
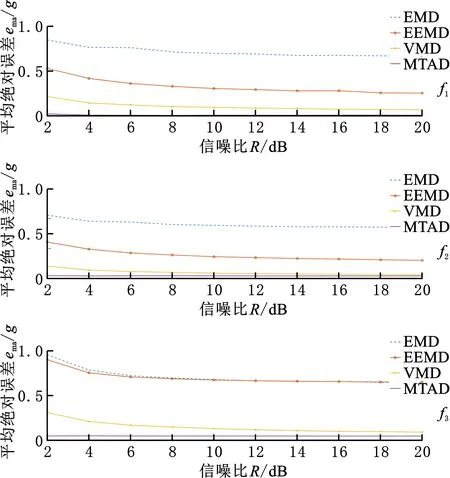
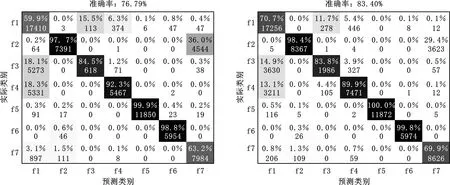
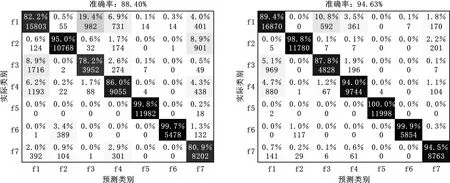
式中,0≤t 时域同步平均法可以将与机械旋转频率对应的基频和倍频信号有效地提取出来,且对噪声以及非相关的信号具有很好的消除和抑制效果[16]。时域平均的本质是由一系列等距分布的带通梳状曲线及其旁瓣组成[17]。值得一提的是,当叠加次数N值较小时,TSA法的抗干扰性能较差。当需要分析低频信号时,取时长较长的原始信号,以防N值较小而难以达到预期效果。 上述方法实现的前提是需获得机械的键相信号,而这正是该方法的局限性之一。此外,由于梳状滤波器的特性,相关倍频信号会被融合到一起而难以分解。而且在旋转机械的振动信号中,周期不为T的其他周期信号中也存在与故障相关的信息。此方法在去除噪声的同时也会将许多有用信息一同抹除,造成某些故障特征的丢失。基于传统的时域平均法,本文提出了时域平均分解法,有效地克服了上述问题。 MTAD基于传统时域平均法,从高频开始提取多个频率下的信号波形,将其与原信号对齐并分解;全面地分析振动信号中不同频率下的信号的特征,较为完整地保留原始信号中所有频率下的故障特征信号,并且抵消了倍频信号的相干影响。需要提出的是,信号要分解的最高频率由故障类型决定,最高频率应大于所有可能存在故障信息的频率,无法确定故障信息频率时最高频率一般可取0.5倍采样频率。该方法表述如下: (1)设信号时长为t,令fs=0.5Fs-is,对周期为T=1/fs的信号做时域同步平均。Fs为采样频率;s为步长,一般可取s=200/(tFs);i为迭代次数且i (2)将原始振动信号Y按周期T分割成K段信号,则可以得到 (6) (7) (4)增加迭代次数i,对Yr重复步骤(1)~步骤(4),直到迭代次数超出约定条件。 (5)最后得到的残差Yr和不同周期下的时间序列Yfs即为时域平均分解的结果: Y=Yr+∑Yfs (8) 在时域平均分解时,每次分解都对信号进行了三次样条插值,这是因为对离散信号应用TSA时相位误差会累计,从而对结果产生较大的影响。沈国际等[18]对误差累计机理做了较详细的阐述。相比其他插值方式,笔者发现使用三次样条插值可以很好地消除误差累计。 MTAD利用TSA的幅频响应特性,从高频开始依次将信号分离出来,从而避免了TSA中指定频率信号与相应倍频信号混叠的问题。每个分解信号可以代表其对应频率的信号特征,并且对不同频段内的分解信号进行重构后得到的信号包含该频段的特征。如对于频段[fs1,fs2]的重构信号,定义为 (9) 重构的信号包含指定频段下的故障特征。基于MTAD重构信号可以使分类器更有效更准确地识别故障,在第四节中进行试验验证。采用多尺度时域平均分解法,在没有键相信号的前提下,可以将与故障相关频段的信息提取出来,同时也将不同频率下的信号有效的分离开来,有效地克服了时域平均法存在的不足。 船舶机舱环境较为复杂,其环境中的干扰信号成分复杂多变。为了证明MTAD方法的有效性,设电机回转频率为25 Hz,构建以下仿真信号: (10) 其中,f1、f2、f3是电机回转频率的1、2、4倍频故障信号分量。为模拟机舱复杂环境,并测试算法对调频信号分解性能,4倍频附近信号f3设置为调频信号。测试分解算法的抗干扰性能,在回转频率2倍频附近加入变频干扰信号fn1。fn2为随机白噪声信号,幅值在-1.3~1.3之间。基于式(10),以1 kHz的采样频率取长度为20 s的仿真信号,其0~1 s内的时域波形如图1所示。 图1 仿真信号时域波形Fig.1 Time-domain waveform of simulated signal EMD[19-21]、VMD[22-24]是较为常用的分解方法。EMD存在模态混叠现象,EEMD可通过添加白噪声以解决该问题。近年来,EEMD在故障诊断领域也得到了广泛的应用[25-26]。分别使用EMD、EEMD,VMD和MTAD方法对信号进行分解。EMD和VMD模态个数设置为4。EEMD方法的集成聚类次数设置为100,添加白噪声的标准差为0.3。MTAD方法以电机回转频率的基频和倍频fs1=25 Hz、fs2=50 Hz、fs3∈[97,103] Hz三个频段重构信号,得到三个分量A1、A2、A3。对EMD、EEMD和VMD分解后的各个模态分量(intrinsic mode functions,IMF),再通过其主频与仿真信号y(t)中各个分量进行匹配。IMF1~IMF4分别表示EEMD分解后第一至第四个模态分量。上述三种方法对y(t)分解的结果如图2所示。 (a)EMD (b)EEMD (c)VMD (d)MTAD图2 不同方法对仿真信号的分解结果对比Fig.2 Decomposition results of simulation signals by different methods 由图2a可以看到,EMD分解时各个模态之间混叠较为严重,与原信号中各个分量相差较大,其结果并不理想。由图2b可以看出,EEMD分解后IMF1偏差较大,IMF3存在一定偏差,IMF4效果相对较好。由图2c可看出,VMD分解后其模态IMF2、IMF4与仿真信号中的f1、f3分量可以较好地对应。仔细观察IMF2、IMF4可以看到0点附近的信号存在一定的偏差,这是因为VMD在原信号两侧镜像一半长度来扩展信号,该方法虽然可以有效改善VMD中存在的端点效应,却不能完全消除其影响。此外,仿真信号中变频干扰fn1的存在,导致IMF3受到了较为严重的影响,对仿真信号中的fn1和f2并未进行有效的分离。观察图2d可以看到,MTAD有效地分解出仿真信号中的3个分量,并且对噪声信号fn1、fn2的抗干扰能力很强,几乎没有受到影响。这是因为TSA的特性,目标频率以外的噪声得到了有效抑制。图3所示为以电机回转频率对y(t)进行时域同步平均的结果。可以看出,该方法受噪声影响很小,对噪声有较强的抑制效果。但是,基频分量f1与倍频分量f2出现了混叠现象。而在图2d中可以看到MTAD对f1、f2进行了有效分解,克服了TSA方法基频与倍频信号波形混叠的问题。 图3 仿真信号时域同步平均结果Fig.3 Time-domain synchronization average result 4种分解方法与仿真信号3个分量之间的绝对值之差如图4所示。可以看出,EMD对原始信号中各个分量的分离偏差较大,每个模态的误差都远大于其他两种方法的误差。EEMD方法误差总体小于EMD方法误差,对分量f3进行分解时误差较大;分量f2分解误差与VMD方法相差不大;分量f1分解受到了一定的噪声影响,误差忽大忽小。而VMD对分量f1、f3的分解结果误差相对较小,由于端点效应只在端点处存在较大误差,但是f2的分解结果受干扰较严重,偏差较大。MTAD的重构信号对原始信号中3个分量的还原度最高,误差最小,对分量f2的分解结果受到了一定的影响,但其误差远小于其他3种方法误差。相比之下该分解方法优势明显。 图4 不同方法与仿真信号的绝对误差Fig.4 Absolute error between different methods and simulated signals 通过以上分析可以看出,MTAD对目标频率范围内的信号可以达到非常好的分离效果,并且对其附近频率范围内的干扰信号有很强的抑制作用。仿真信号分析中,运用了fs1、fs2、fs3三个预设频段,但是在实际应用时,往往不知道故障对应的特征频率,这时就需要对MTAD全频段分解的结果进行进一步分析。笔者引入了模糊熵特征选择方法,对分解后的信号进行故障特征选择,从而确定故障特征频率并优化分类器性能。 为了不失一般性,对不同信噪比信号进行分析,构建以下仿真信号: (11) 其中,f1、f2、f3是3个不同频率下故障信号分量。基于信号y(t)以1 kHz的采样频率取长度为20 s的仿真信号,其0~1 s内的时域波形如图5所示。 图5 仿真信号时域波形Fig.5 Time-domain waveform of simulated signal 向信号中加入不同信噪比的高斯白噪声,使原始信号中的信噪比取值范围为2~20 dB,构成含噪声的信号yn(t)。分别使用EMD、VMD和MTAD方法对信号进行分解,并计算不同信噪比下分解信号与原始信号中故障信号分量的平均绝对误差(mean absolute error)。平均绝对误差ema的计算公式为 (12) 式中,m为信号长度;x为原始信号中的特定分量;fxi为原始信号分量fx中的第i个点的数值;IMFxi为对应分解信号IMFx中第i个点的数值。 在不同信噪比下,分别使用EMD、EEMD、VMD和MTAD方法对yn(t)进行分解,计算不同模态分量与原始信号中f1、f2、f3三个不同分量的平均绝对误差,结果如图6所示。 图6 不同信噪比下各方法的平均绝对误差对比Fig.6 The average absolute error of each method under different signal-to-noise ratio 由图6可以看出,4种方法的平均绝对误差都随着信噪比的增大而增大。但是MTAD分解后对应的3个分量平均绝对误差都较小,而且改变信噪比对该方法影响不大。EMD的平均绝对误差较大,相比之下抗噪声效果较差。除f3外EEMD效果介于EMD和VMD之间,f3分量的分解效果与EMD几乎相同。而VMD在信噪比较大时效果尚佳,信噪比较小时抗噪能力较差,尤其是信噪比低于8 dB以后VMD的误差明显增大。综上可知,MTAD方法的抗噪声能力非常强,而且适合在不同信噪比环境中运用。 LUUKKA等[27]、LOHRMANN等[28]对模糊熵特征选择的原理及过程已经做出比较详细的解释,简述如下。 分类器通常会将样本分为i个类别。分类器基于某类的标准向量v和样本集中的向量x之间的相似度S〈v,x〉来判定x是否属于该类。相似度S越趋近1则表明该样本属于该类,越趋近0表明该样本不属于该类。对于N个特征值的样本,需要计算N个相似度SN,当特征值的相似度越低或者越高时则表明该特征值的确定度高,其对应的模糊熵值越低,有利于样本的区分。特征值相似度越接近0.5则表明该特征值的不确定度越高,其对应的模糊熵值越高,不利于样本的区分。定义样本特征的模糊熵为 (13) 其中,k=1,2,…,N。N为特征向量个数。wj为当前特征值的权重。Sk=〈xj,vk〉为第k项特征值样本xj与标准向量vk的相似度。 模糊熵值的高低代表该特征项对分类器的贡献度。通过计算每个特征的模糊熵值,将模糊熵较高的特征值去除,只保留i个模糊熵较小的特征值。i值越小,分类器运算速度越快,但准确率也越低,所以在保证分类准确的前提下,i值应尽可能地小。上述方法可以去除特征提取后的冗余信息,保留有效信息,从而达到优化分类器运算速度和提高分类准确率的目的。 利用船舶旋转机械进行故障模拟试验,对本文方法进行有效性验证。机器学习算法在机械故障诊断领域已得到广泛运用[29],其中特征提取和分类器的选择共同决定了故障诊断的优劣。本文着重讨论使用MTAD进行特征提取和模糊熵特征选择方法的效果,上述方法可与不同分类器结合使用。支持向量机(support vector machine,SVM)是经典的机器学习分类器,它应用简便高效、效果良好、性能稳定,是故障诊断领域普遍使用的分类器之一。本文选用SVM作为故障识别的分类器,试验数据处理流程如图7所示。步骤如下: 图7 试验数据处理流程图Fig.7 Test data processing flowchart (1)分别取机械正常状态和不同故障状态下的多组数据,将得到的正常信号和几种故障信号进行MTAD分解。 (2)对MTAD分解出所有频率下的时间序列以波峰绝对值进行模糊熵特征选择,从中选择n个模糊熵较小的时间序列重构特征信号。 (3)从数据集中随机选取多个数据构建训练集,剩余数据组成特征集。使用训练集训练SVM。使用训练好的SVM模型对测试数据进行准确性和有效性验证,重复多次并分析诊断结果。 本文以三相异步电动机驱动的船用风机作为试验对象。设置正常状态、扇叶不平衡故障、风机底座松动故障、电机底座松动故障、风机堵转故障、扇叶不平衡和电机底座松动复合故障、扇叶不平衡轻微故障七种模式,上述七种电机运行状态分别对应状态代码f1~f7。试验中,风机的电机额定电压为380 V,额定电流为4.6 A,额定功率为1.1 kW,额定频率为50 Hz,额定转速为1400 r/min。振动传感器使用磁吸式传感器,其灵敏度为10.20 mV/g,偏置电压为12.40 V。振动信号的采样频率为1652 Hz,每组信号的采样时长为2 s,每次试验采集20组数据。对f1~f7七种不同状态下的风机做多次重复试验,共计得到2460组试验数据。试验布置及测点如图8所示。 图8 故障模拟试验测点布置Fig.8 Layout of measuring points for fault simulation test 对上述试验得到的振动数据使用MTAD分解,步长设置为s=0.5。不同状态下的电机振动信号与MTAD分解后信号的频谱图见图9。可以看出,由于机舱环境复杂,电机振动信号中高频干扰严重。此外,由于MTAD基于TSA方法分解,前文提到当原始信号时长较短时对低频信号的分解并不理想。还可看出,10 Hz以下的频率范围内对应振幅偏大,这是因为叠加次数较少,难以将低频信号与噪声进行有效的分离。但试验中电机额定转速为1400 r/min,对应回转频率在23.3 Hz左右。低频信号中并未包含过多的有用信息,不会对试验结果造成影响。在特征选择时会将这些信号与其他冗余信息一起筛除。 仔细观察图9不难发现,某些故障与旋转机械的回转频率和回转频率相关倍频信号存在关系,如f2、f4、f6、f7。还可看出f1、f3、f5的倍频信号没有明显特征,其故障信息很可能包含在其他频率范围的信号中。因而引入模糊熵特征选择,计算每个频率下信号的模糊熵,以确定不同故障模式对应的特定频率范围。 使用EMD、EEMD、VMD分解原始振动信号,其中EMD不设置模态上限,取前5个IMF作为结果。EEMD的集成聚类次数设置为100,添加白噪声的标准差为0.3,取前5个IMF。VMD的IMF设置为5。用EMD和VMD各个模态的频谱作为特征值,MTAD使用分解后各频率下幅值绝对值最大值为特征值。将各种状态下的数据随机挑选20%作为训练数据训练SVM并计时,使用所有数据对训练好的SVM进行测试。为防止异常数据干扰,对上述方法进行30次循环重复试验,并记录每次的预测准确率和训练耗时。不同分解方法对应的分类器混淆矩阵如图10所示。 (a)正常 (b)扇叶不平衡 (c)风机底座松动 (d)电机底座松动 (e)风机堵转 (f)扇叶不平衡加底座松动复合故障 (g)扇叶不平衡轻微故障图9 电机各种故障模式下振动信号与MTAD分解信号频谱图Fig.9 Vibration signal and MTAD decomposition signal spectrum under various failure modes of the motor (a)EMD-SVM混淆矩阵 (b)EEMD-SVM混淆矩阵 (c)VMD-SVM混淆矩阵 (d)MTAD-SVM混淆矩阵图10 不同分解方法的混淆矩阵Fig.10 Confusion matrix of different decomposition methods 使用EMD、EEMD、VMD、MTAD提取特征,SVM的平均预测准确率分别为76.79%、83.40%、88.40%和94.63%。训练平均耗时分别为2.62 s、2.55 s、4.42 s和1.23 s。为了与传统TSA方法进行对比,以风机回转频率对原始振动信号进行TSA处理,将分解后结果的绝对值的最大值和均方根值(root mean square,RMS)作为特征值训练SVM。五种方法SVM训练结果如图11所示。 图11 分类准确率与训练耗时Fig.11 Classification accuracy and training time TSA平均准确率为39.3%,远低于其他四种方法。这是因为前文所述TSA可以将回转频率的故障特征提取出来,但同时丢失了其他频域的故障信息。而且在第二节仿真信号分析中可以看到,TSA分解的波形会与倍频信号混叠,所以TSA方法在对本实验中的多种故障、轻微故障、复合故障进行识别时效果并不理想。 由图10和图11可以看出,基于MTAD分解的SVM识别准确率高于其他几种方法,这主要是因为船舶机舱中环境噪声较大,噪声成分复杂,噪声中含有多种变频变幅信号与爆振信号,容易对EMD、EEMD和VMD的结果造成影响。而MTAD在多噪声多干扰的环境中,继承了TSA的抗噪特性,对噪声的抑制能力较强。在前文仿真试验中也可以看到VMD对特定频率附近的噪声抗干扰能力较差,而EMD多个模态之间容易出现混叠。在图10中可以看到EMD和EEMD在对f2和f7进行分类时的错误率较高,容易将f2错分为f7。VMD也受到了一定影响。而MTAD方法分类效果较理想,只有2.2%的错误率。MTAD方法只有将f1错分到f3的错误率较高,但与其他方法对比错误率仍然最低。可以看出MTAD方法可以更有效地从原始振动信号中提取机械故障信息,有助于分类器正确分类。 SVM训练耗时主要是受特征序列维度的影响。EMD、VMD分别使用4956和8265个高维特征序列,所以导致SVM训练速度较慢。而MTAD分解后的频率特征序列维度为1652,因此其训练速度优于其他两种方法。TSA虽然训练速度最快,但是其准确率远达不到理想效果。 上述结果证明了MTAD分解方法的有效性。下面通过模糊熵特征选择进一步优化SVM故障识别的效率。 对MTAD分解得到的特征值进行归一化处理后,利用模糊熵值进行特征选择,所有特征项对应的模糊熵值如图12所示。去除模糊熵值高的特征项,保留模糊熵值较低的特征项并构成数据集。利用该数据集对支持向量机进行训练和验证,通过改变保留的特征项个数优化支持向量机的运算速度与准确率。特征项保留越多,SVM训练速度越慢,减少特征项可以提高SVM效率,但过度筛除特征项会导致故障信息的丢失,使得SVM的准确率降低。进行合适的特征筛选有助于实现准确高效的故障诊断。 图12 各特征项归一化模糊熵值Fig.12 Normalized fuzzy entropy value of each feature 从MTAD分解得到的1652个特征中每次筛除50个特征值,使用剩余的特征项训练SVM,记录准确率并计时。每次训练随机挑选20%的数据作为训练集,每组数据循环验证20次。保留的特征项个数与准确率箱形图见图13,准确率均值由箱形中央横线表示。 图13 保留特征数量与SVM准确率Fig.13 Retained features number and accuracy of SVM 由图13可以看出,筛除少数模糊熵较低的特征值时SVM平均准确率会上升,随着保留特征数量的减少,平均准确率也会随之下降,平均准确率分别在1252和802特征数量处大幅下降,当保留数量为852时,准确率均值为93.31%。而继续剔除特征项会导致准确率大幅降低,保留802个特征值时准确率只有90.16%,准确率下降了3.15%。很有可能是因为在继续筛除特征项时筛除了与故障相关的特征,致使某些故障无法正确识别。 保留特征项训练耗时见表1。由表1可以看出:随着保留特征项的增加,模型训练耗时也逐渐增加。结合图13并通过计算得出,当保留1402个特征项时平均准确率达到最高,为94.94%,比保留全部特征项时准确率提高了0.53%,同时计算速度提高了111.47%。这说明筛除无关特征项不仅会提高分类器运算速度,而且能排除无关干扰项从而提高分类器的准确率。当追求运算速度时可以保留852个特征项,使运算速度提高154.26%。当追求准确率时可以保留1402个特征项,使平均准确率达到最优。 表1 不同特征数SVM计算耗时Tab.1 Time-consuming calculation of SVM with different feature numbers 综上可知,与EMD和VMD相比,使用MTAD可以对原始数据进行更有效的特征提取。MTAD方法在船舶机舱等含有多种噪声信号干扰的环境中抗噪声能力强,且使用MTAD作为特征项进行训练的分类器对故障的识别率更高。使用模糊熵对MTAD分解得到的特征项进行特征选择后可以进一步提高分类器的准确率和计算速度。保留1402个特征项时可以使分类器准确率达到94.94%,保留852个特征项时可以使分类器训练速度提高154.26%。上述结果证明了MTAD结合模糊熵特征选择可以有效地实现船舶旋转机械故障诊断。 相比传统的时域同步平均法,MTAD方法可以有效分离倍频信号,并且不会丢失某特定频率外的故障信息,同时也无需获取键相信号。该方法克服了传统方法的局限性。MTAD结合模糊熵特征选择,可以有效地去除冗余信息从而提高分类器的运算速度和准确率。通过仿真数据分析和故障模拟试验数据分析验证了该方法的有效性,得出结论如下: (1)旋转机械的振动信号中,电机转速对应回转频率之外存在与故障相关的信息,使用本文方法可有效提取出相应特征。 (2)MTAD可以在没有键相信号的条件下对振动信号进行特征提取。相比EMD、EEMD和VMD方法,MTAD方法对指定频率范围之外的噪声和干扰信号有较强的抑制作用,可以更好地从振动信号中提取故障信息。 (3)MTAD结合模糊熵特征选择可以准确高效地实现船舶旋转机械故障诊断。 综上,所提方法简单快捷,对实现船舶机械智能故障诊断有重要的参考价值,可以有效地运用在船舶机舱等噪声成分复杂的环境中。1.2 多尺度时域平均分解法(MTAD)
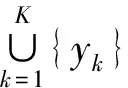
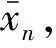

2 仿真信号分析





3 模糊熵特征选择
4 试验分析
4.1 试验分析流程

4.2 试验设备与故障设置

4.3 方法对比








4.4 特征选择
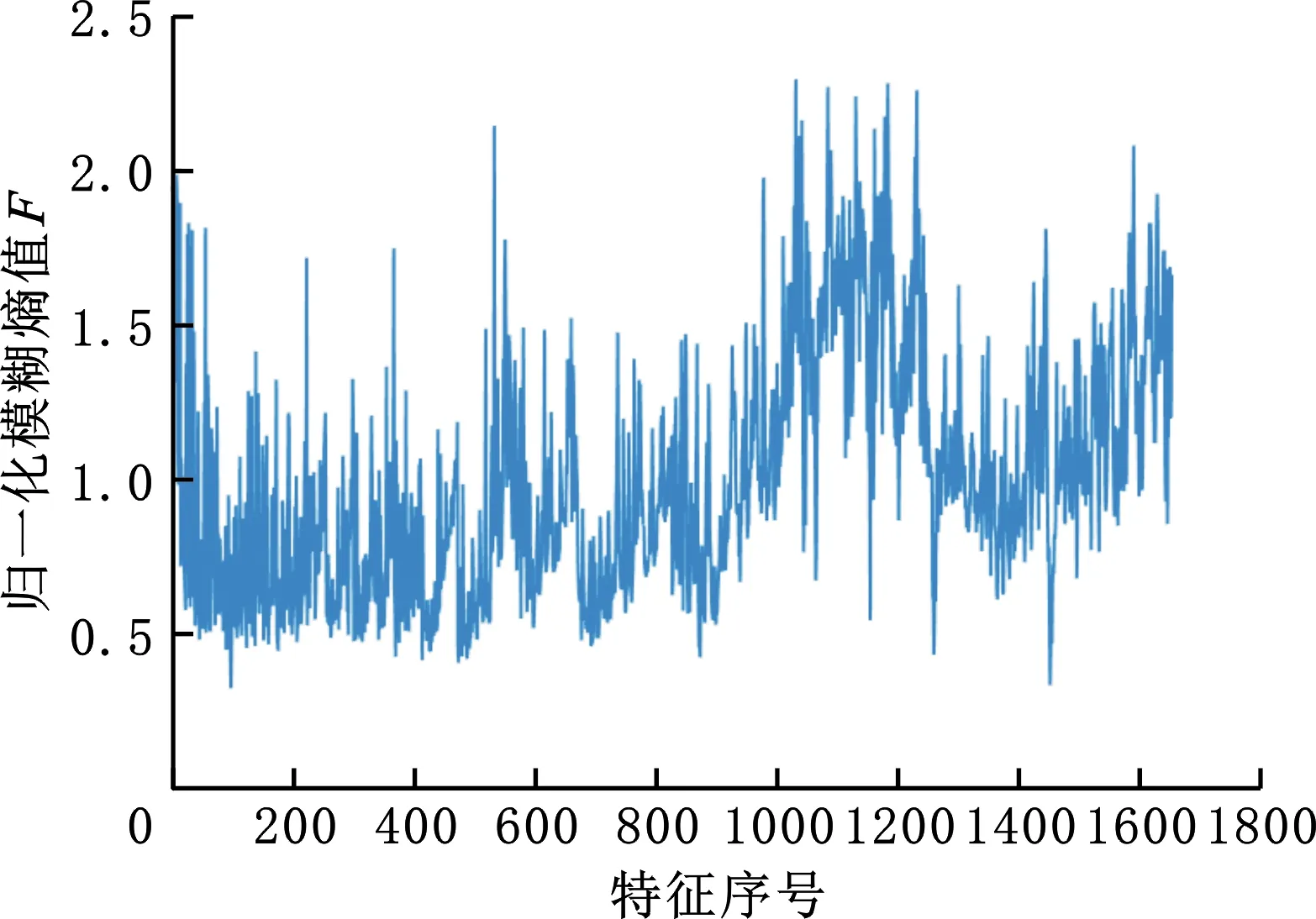
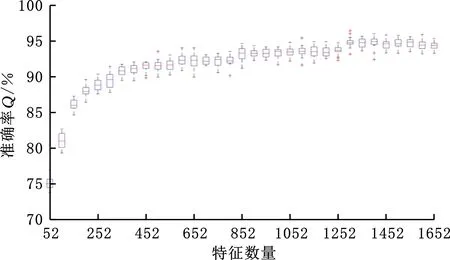
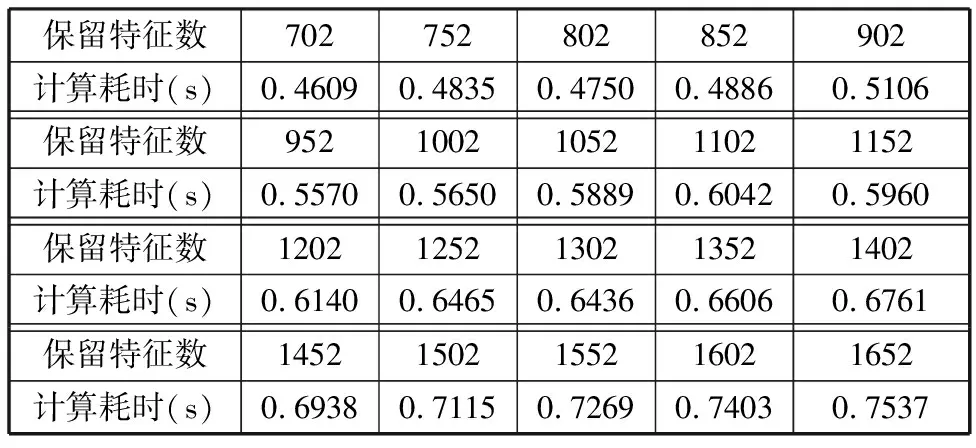
5 结语
