基于块稀疏二维联合模型的双基地ISAR高分辨成像算法
2022-05-31吴云军黄国鹏陈文峰
吴云军,黄国鹏,陈文峰
(1.火箭军装备部驻武汉地区第二军事代表室,湖北 武汉 430000;2.空军预警学院,湖北 武汉 430019)
双基地逆合成孔经雷达ISAR(inverse synthetic aperture rader)具备双基地雷达收发分置的优势,同时利用逆合成孔径技术进行成像,不仅能有效对抗“四大威胁”[1],而且能获得包含目标结构和形状等信息的高分辨二维图像。因此,双基地ISAR技术在目标监视、成像和识别等军事和民用领域都具有非常重要的意义[2],双基地ISAR成像技术已成为现代雷达技术研究的新热点[3-4]。
双基地ISAR距离向分辨率受雷达发射信号带宽的限制,而方位向的分辨率则取决于成像积累角的相干积累,并且距离分辨率和方位分辨率都与双基地角有关,且双基地角越大分辨率越低。为提高有限带宽有限脉冲条件下双基地ISAR成像的距离和方位二维分辨率,压缩感知被引入到双基地ISAR成像中,文献[5]在距离向和方位向分别利用压缩感知实现了成像处理,取得了相比传统RD(range doppler)方法更好的双基地ISAR成像效果,但是这种解耦处理破坏了回波的二维联合稀疏结构。为利用二维联合稀疏结构,文献[6]基于二维联合稀疏模型,提出一种低信噪比条件下二维联合的快速高分辨双基地ISAR成像方法,具有较低计算复杂度和较强的噪声鲁棒性能。然而,实际的双基地ISAR图像通常具有块稀疏结构的特点,因此图像中的散射点通常呈现出聚集的块稀疏结构。因此,笔者对这一先验信息加以利用,以进一步提升成像性能。
笔者基于块稀疏二维联合模型,提出了基于二维联合模型下矩阵迭代重赋权复数近似消息传递(matrix-formed iteratively reweighted complex approximate message passing based on two dimensional coupled dictionaries, MIRCAMP-TCD)算法的双基地ISAR成像算法。首先将块稀疏二维联合成像问题转换为重赋权1最小化问题,其次利用重赋权1最小化框架进行迭代求解,每次迭代中的加权1最小化问题利用近似消息传递CAMP(complex approximate message passing)算法求解,然后利用向量化算子的性质导出了矩阵形式的迭代重赋权算法,由前一次稀疏解对应的系数及其附近的系数实现权值的更新。
1 双基地ISAR二维联合成像模型
考虑加性噪声的影响,双基地ISAR二维联合成像模型为[7-8]:
Y=ΦSΨT+E
(1)
式中:Y为回波信号;Φ为距离维感知矩阵;Ψ为方位维感知矩阵;S为待重构的二维图像;E为复高斯白噪声。
图1为VFY-218飞机的双基地ISAR图像及块稀疏结构,从图1可知,图像中的散射点呈现出聚集的块稀疏结构,当某个幅度非零的散射点位于(m,n)时,其附近的散射点的幅度很大概率也是非零的。如果在二维联合高分辨成像时充分利用这一先验信息,则有望提升成像算法的重构性能。

图1 VFY-218飞机双基地ISAR图像及块稀疏结构
2 基于MIRCAMP-TCD算法的二维联合超分辨成像
MIRCAMP-TCD算法首先将块稀疏二维联合成像问题转换为重赋权1最小化问题,其次利用重赋权1最小化框架进行迭代求解,每次迭代中的加权1最小化问题利用CAMP算法求解,然后利用向量化算子的性质导出了矩阵形式的迭代重赋权算法,由前一次稀疏解对应的系数及其附近的系数实现权值的更新。
为求解式(1),通过矩阵乘积的向量化与Kronecker积的变换性质[9],对式(1)进行向量化处理:
vec(Y)=(Ψ⊗Φ)vec(S)+vec(E)
(2)
式中:vec(·)为矩阵的列向量化操作;符号⊗表示Kronecker积。
令y=vec(Y),s=vec(S),A=(Ψ⊗Φ),e=vec(E),则式(1)变为:
y=As+e
(3)
min‖Wθ‖1
s.t.‖y-Aθ‖2≤ζ
(4)
其中,W为对角矩阵。
(5)
式中:diag(·)的输入为向量时则生成以该向量元素为主对角线的矩阵。当diag(·)的输入为矩阵时,则生成一个向量,其元素为输入矩阵的主对角线;eps为一个很小的正数;θ为S的估计值;‖·‖1表示1范数;‖·‖2表示2范数;W为权矩阵;ζ为噪声能量。
为更加有效地求解,文献[10]给出了一种修正形式:
min‖x‖1
s.t.‖y-AW-1x‖2≤ε
(6)
式中:x为θ加权后的结果;x和θ的关系为θ=(W)-1x。
对于不同的权矩阵,式(6)有不同的解。文献[11]指出,如果正确的设置权值,就能够提高重构性能。当权值能够抵消信号幅度对1范数罚函数的影响,此时重构性能就能够提高。大权值用来压制重构信号中的非零元素,小权值用来增强非零元素。由于x是稀疏的,其较小的系数对应较大的权值,而较大的系数对应较小的权值。较小的权值能够增强较大系数的重构,而较大的权值将会抑制较小系数的重构,在下一次重构中,对应较大权值的较小系数将会变得更小,经过几次迭代,即可得到更为稀疏的解。

(7)
式中:xt为第t次迭代重构结果;vt为中间变量;zt为残差项;η为复数软阈值函数;ηRe和ηIm分别为复数软阈值函数的实部和虚部;〈·〉表示求平均;δ为采样率;γt=τσt为软阈值门限;τ为调整参数;σt为该次迭代中噪声的标准差;B=AW-1。
然而,式(7)中感知矩阵规模非常大,需要很大的存储空间和计算复杂度。为了提升成像效率,减少存储空间并且降低计算复杂度,根据向量化算子的性质,得到式(7)的矩阵化形式为:

(8)
式中:W1=unvec(diag(W-1)),unvec(·)为向量的矩阵化算子;Vt,Zt,Zt-1分别为vt,zt,xt-1的矩阵化形成;(·)*表示共轭。
(9)
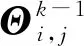
新的权值为相邻系数建立了相互关系,因此更适用于具有块稀疏结构信号的重构。利用式(8)求解迭代重赋权1最小化问题,按照式(9)进行权值的更新,此时就得到了MIRCAMP-TCD算法,其基本迭代公式为:
(10)
其中,Xk和Θk之间的关系为:
Θk=(Wk)-1Xk
(11)
3 性能分析
3.1 计算复杂度和内存要求
相比文献[6]的MCAMP-TCD算法,MIRCAMP-TCD算法需要经过几次迭代(一般在10次以内)便能够得到较好的重构结果,假设迭代次数为L,那么MIRCAMP-TCD算法的计算复杂度为O(2QNlog2NL+2NQlog2QL),其中,Q、N分别为待重扬二维图像S的列数和行数。
对于内存要求而言,MIRCAMP-TCD算法仅增加了权矩阵,因此MIRCAMP-TCD算法相比MCAMP-TCD算法仅增加了16 MB,因此MIRCAMP-TCD算法的内存要求也是比较低的。
3.2 重构性能
新的权值更新方式适用于块稀疏信号的重构,在重构时,由于权值的原因,会使得聚类的这一部分元素得到积累,相比单独的一个元素,在阈值收缩时更容易突破阈值的限制,成为重构信号的非零元素。因此,在相同量测值条件下,MIRCAMP-TCD算法相比MCAMP-TCD算法具有更高的重构概率;在相同信噪比时,MIRCAMP-TCD算法相比MCAMP-TCD算法具有更强的抗噪能力。
4 实验与分析
为验证笔者提出的MIRCAMP-TCD算法的成像性能,通过电磁计算软件FEKO7.0生成双基地ISAR数据,成像目标为VFY-218飞机,仿真参数如表1所示,对比方法为文献[6]提出的MCAMP-TCD算法。
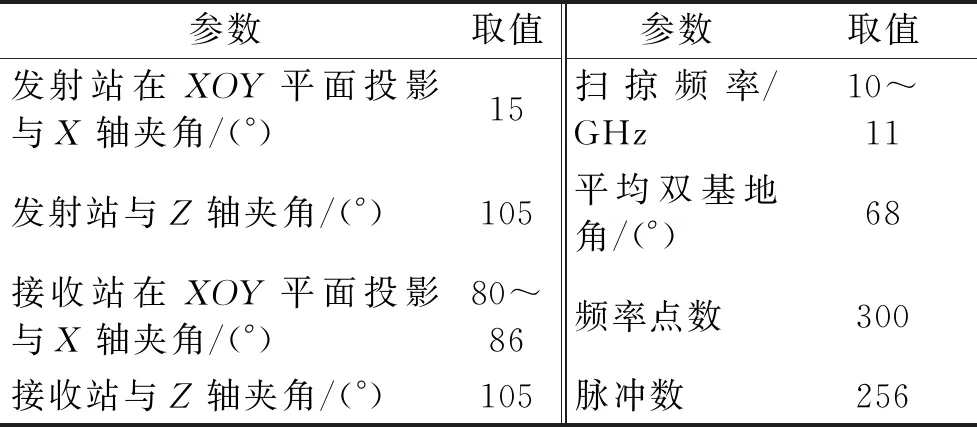
表1 双基地ISAR成像电磁计算参数设置
不同采样率电磁计算双基地ISAR数据成像结果如图2所示。从图2可和,在相同采样率的条件下,由于MIRCAMP-TCD算法利用了块稀疏结构,相比MCAMP-TCD算法,成像结果聚焦性能更好,虚假散射点更少,在相同采样率条件下笔者所提算法的成像性能更好。为进一步对比算法性能,考虑不同采样率δ条件下的成像性能对比,图3(a)~图3(e)分别给出了两种算法得到的IE(image entropy)、IC(image contrast)、TBR(target to background ratio)、CC(correlation coefficient)以及成像时间的对比曲线。

图2 不同采样率电磁计算双基地ISAR数据成像结果
从图3(a)~图3(d)能够明显看出,MIRCAMP-TCD算法得到的IE更小、IC更大,说明该本文算法得到的双基地ISAR图像聚焦性更好;同时该算法得到的TBR和CC更大,说明成像结果虚假散射点更少,与参考图像更接近。从图3(e)可知,MIRCAMP-TCD方法成像时间有所增加,这是因为该算法需要在MCAMP-TCD算法基础上迭代处理。仿真验证了本文方法对于块稀疏目标具有更好的欠采样成像能力。
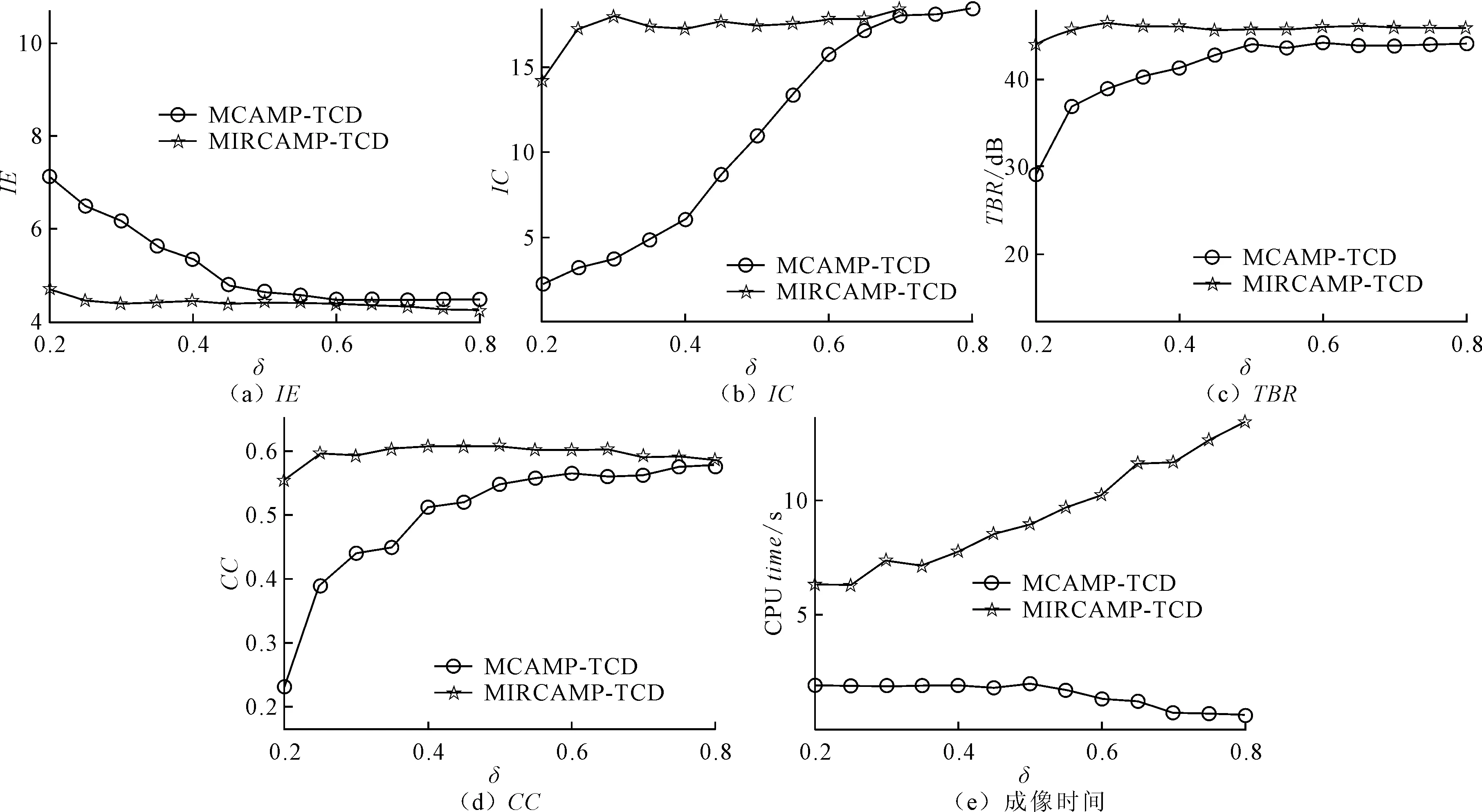
图3 不同采样率下成像性能曲线
5 结论
为利用目标的块稀疏特性以提高有限数据下双基地ISAR成像性能,笔者提出了基于块稀疏二维联合模型的双基地ISAR高分辨成像算法。首先分析了二维联合成像中块稀疏结构,实际的双基地ISAR图像具有块稀疏结构的特点,在二维联合高分辨成像时充分利用了这一先验信息,进一步提高了成像性能。基于电磁计算的双基地ISAR成像数据验证了所提算法能够提高块稀疏目标的重构性能。
