一种用于WSN的低功耗稀疏参数估计策略

李 林

(天津商业大学信息工程学院，天津 300134)

0 引言

WSN用于目标定位与追踪、频谱感知、自动雷达、导航及机器视觉等领域时，常需要节点协同估计同一个未知参数[1]。WSN中的每个节点用一组输入观测未知参数，由于环境复杂这些观测值是未知目标参数受多元噪声(如环境或测量噪声)干扰后的观测值，由这些观测数据所得到的参数与原始目标参数相去甚远[2]。所以，如何从噪声干扰中精确地估计出原始目标参数是一个重要的问题[3]。参数估计算法已经有了大量的研究，通常会选用一些自适应算法作为参数估计算法，如线性预测算法、最速下降算法、递归最小二乘算法、平方根自适应算法和最小均方自适应LMS(least mean square)等。

本文基于CS提出了一种用于WSN稀疏参数估计的自适应压缩融合重构(compressed combined reconstruct adaptive，CCRA)。首先，节点先将本地的全维参数估计值由一个感知矩阵变换到低维的估计值，即将估计值压缩，节点仅传输压缩后的估计值；其次，节点收集其邻居节点压缩后的估计值和自身的本地压缩后的估计值融合。然后，节点通过重构算法精确地重构出全维的估计参数。最后，每个节点LMS 算法更新下一时刻自身的估计值，其中步长选用归一化步长。CCRA 算法在不影响网络的估计性能情况下，降低了网络的通信负载。

本文首先描述WSN参数估计的问题，介绍了参数估计的数学模型；然后分析了基于LMS算法的估计策略，给出了集中式策略和分布式策略的理论推导，并分析二者特点；提出了一种用于WSN稀疏参数估计的CCRA策略，针对稀疏参数估计引入了CS理论；最后通过仿真与结果分析，对CCRA策略与其他策略进行了对比分析，说明各自的有效性。

1 WSN参数估计

本文研究一个有N个节点的WSN。WSN参数估计的线性回归模型可表示为

di(t)=WToui(t)+vi(t)

(1)

式中：di(t)为标量观测值；ui(t)为节点i在t时刻的回归向量；Wo为未知的目标参数向量；vi(t)为节点在观测未知参数时的干扰。

2 LMS策略

本节给出了参数估计的集中式LMS策略以及分布式LMS策略的原理和数学推导过程。

2.1 集中式LMS策略

为得到接近原始的未知目标参数wo的估计值w，需要将参数估计的全局代价函数最小化，全局代价函数Jglobal(w)可表示为

(2)

式中E为期望。

假设ui是联合广义平稳随机过程，则集中式LMS算法的递归公式可表示为

(3)

式中：μ为递归表达式的步长，μ>0；w(t)为t时刻对未知参数wo的先验估计。

由式(3)可以看出，集中式策略每轮都需要一个中心节点来收集和处理网络中所有节点的估计信息，这将带来很大的通信负载。如果网络中的节点之间通信链路失效或者更改，集中式LMS策略就很难运行，鲁棒性较差。

2.2 分布式LMS策略

分布式LMS增量策略是最简单的分布式策略，增量策略中节点的估计信息经过一个单向的哈密顿回路在节点之间传递，每个节点将其信息传输给同方向的下一节点。对给定拓扑的传感器网络，这种策略在节点数目较多和拓扑复杂时鲁棒性较差。

在分布式共识和扩散LMS策略中，每个节点只需要与邻居节点交换估计信息来获取估计值，如图1所示。如果2个节点可以直接通信，则定义这2个节点互为邻居节点[3]。例如，节点7的邻居节点定义为Ω7，Ω7包含节点7本身。每个节点需要计算其本地估计值，并从邻居节点中获取邻居节点的本地估计。如图1中，箭头表示节点之间的通信链路，节点7的邻居节点集合Ω7为节点3、5、6、7、8。这些节点可以与节点7直接通信。由于网络采用分布式共识和扩散策略，当网络中一些节点不能正常通信，整个网络仍能继续工作。

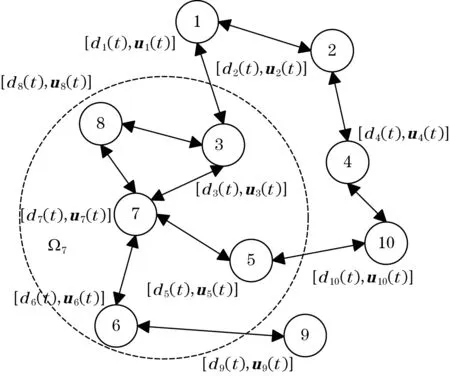
图1 分布式共识和扩散LMS策略

分布式共识和扩散LMS参数估计策略可以分为3个阶段，分别是信息交换阶段、适应阶段和融合阶段。根据网络的拓扑，节点i赋予不同的融合系数来融合每个邻居的估计值：

(4)

式中：γii为节点i自身估计值的融合系数；γij为其邻居节点j在节点i的融合阶段的融合系数。

融合系数需要满足式(4)。

融合系数的计算多种规则，本文中选用的Metropolis规则为:

(5)

分布式共识策略与扩散LMS策略的主要区别是：共识策略在适应阶段用加权融合后的估计值和本地估计值结合用来计算下一时刻的估计值，扩散策略在数据融合后，适应阶段仅用融合后的估计值计算下一时刻估计值。选用分布式扩散LMS策略，并给出推导过程。

分布式扩散LMS策略中，节点需要从自身以及邻居节点的估计值中寻求对未知参数wo的估计。在每个t时刻，节点i对wo的估计值为wi(t)，则下一时刻t+1的估计值的更新方程的递归表达式为

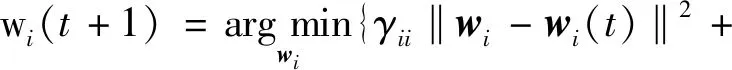
(6)

式中μi为节点i的LMS算法步长。

为了化简更新方程，在wi处用泰勒级数展开式(6)大括号内的最后一项去除步长的部分[di(t)-

uTi(t)wi]2，可得：

(7)

式中eij(t)=di(t)-uTi(t)wj。

同样的，可以将其在wi(t)处也用泰勒级数展开，可得：

[di(t)-uTi(t)wi]2=e2i(t)-2ei(t)·
uTi(t)[wi-wj(t)]+o‖wi‖2

(8)

式中ei(t)=di(t)-uTi(t)wi。

将式(7)和式(8)带入式(6)，因为融合系数满足式(4)，则式(6)可表示为

在过去几十年中，蛋白质组学技术从出现到发展取得了巨大的进步。蛋白质组学技术可以定性、定量分析不同样品中的蛋白质种类及性质[2]。蛋白质组学技术一般包含样品处理、质谱测定和数据分析三个步骤。

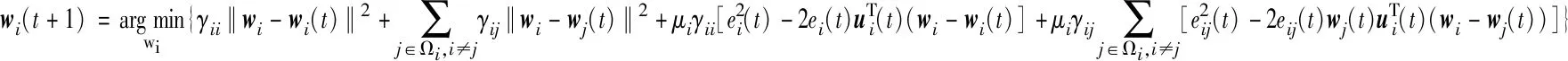
(9)

式(9)中大括号内部的式子是一个关于wi的函数f(wi)。为了得到wi(t+1)，则需要求出使得f(wi)最小的wi：

f′(wi)=0

(10)

则求解关于wi的方程式(10)，可得出wi(t+1)的分布式更新函数为：

wi(t+1)+φi(t+1)+μiui(t)[di(t)-uTi(t)φi(t+1)]

(11)

(12)

式(11)为适应阶段，式(12)为融合阶段。

3 用于WSN稀疏参数估计的CCRA策略

本节引入CS理论，提出了CCRA策略，给出了策略的算法步骤和流程图，并对该策略做了稳定性分析。在本节中沿用第2节的模型，并假定模型中未知参数向量wo是稀疏的，即wo中仅有少量的非零元素，其他元素均为零。

3.1 用于参数估计的CS

由于未知参数wo是稀疏的，若估计值w为准确的，也应该是稀疏的。若直接用标准扩散策略将传输其全维估计值，特别的当维数较高时，通信负载依然很大。CS理论可以通过少量的观测值完整高概率地恢复出原始稀疏向量。当未知目标参数为稀疏向量时，引入CS，可以在完全不影响其估计性能的情况下降低通信负载。

用于参数估计的CS模型可表示为：

(13)

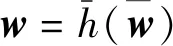
(14)

3.2 CCRA策略

与标准的分布式扩散LMS策略相比，CCRA策略增加了2个阶段，分别是压缩阶段和重构阶段。在每一时刻t，各个节点将自己的本地估计值压缩，计算出本地压缩估计。压缩阶段的方程为

(15)

式中Γi为满足独立同分布的高斯随机矩阵。

邻居节点之间交换各自的本地压缩估计，如式(16)所示：

(16)

(17)

本文提出的CCRA策略将步长μ归一化处理，用μ′代替标准扩散策略中μ，μ′用式(18)计算：

(18)

适应阶段用式(18)得到的全维估计，计算出下一时刻的本地估计值并更新，更新方程如式(19)所示：

wi(t+1)=φi(t+1)+μ′iui(t)[di(t)-uTi(t)φi(t+1)]

(19)

CCRA策略架构如图2所示。

4 仿真结果与分析

本节对提出CCRA策略仿真，与其他策略对比，并分析仿真结果。通信负载包含传输的数据包数量、传输包投递率和传输延迟。本节对比的其他基于LMS的策略与本文提出的2种策略相比，数据包投递率和传输延迟没有区别。所以本节与文献[3，5]相同，在仿真对比中，采用传输的数据包数量来描述整个WSN的通信负载。

本节将用于稀疏参数估计的CCRA策略与其他分布式扩散LMS策略(如DLMS、无合作LMS、NDLMS和RC-LMS)对比。为与其他分布式扩散LMS策略在相同条件下对比，WSN拓扑节点数量N=20。在仿真中，输入回归向量和未知稀疏参数向量的维数M=32，输入回归向量为AR-1[6]过程ui(t)=xi(t)+ρiui(t-1)的一个采样ui(t)=[ui(t)ui(t-1)…ui(t-M+1)]T，相关系数ρi=0.5，xi(t)是一个σx,j=1的白噪声过程。xi(t)是一个σx,j=1的白噪声过程。由于M=32，则回归输入向量ui(t)为32×1的向量。每个节点回归矩阵的迹为Ri=E(ui(t)uTi(t))。仿真时间t=1,2,…,T，其中T=2 000。

每个节点的噪声vi(t)是一个0均值的高斯过程。每个节点的输入回归向量和噪声都在时间和空间上相互独立。仿真中稀疏目标参数向量的稀疏度为2，感知矩阵Γi是一个固定的D×M的高斯随机矩阵D=12，满足R.I.P性质。无合作LMS、DLMS和RC-DLMS这些固定步长策略的步长μ=0.01。自适应步长策略NDLMS和本文提出的CCRA策略设置为μ′=0.4/uTi(t)ui(t)。RC-LMS的能耗参数选为性能和通信负载可以兼顾的0.5。

仿真中所有曲线均为50次独立运行的平均值。图3中可以看出在520轮时，本文提出的CCRA的全局MSD已经低于-50 dB，而其他扩散LMS策略均需要在1 200轮之后才接近于-50 dB。图3中可以看出，本文提出的CCRA策略在收敛速度上快于其他扩散LMS策略，在稳态的性能上优于其他策略。为进一步的分析评估几种策略在稳定状态的网络估计性能，取后500个时刻的数据描述稳定状态，将这500个时刻的瞬时值做平均。如图4所示，CCRA策略在稳定状态的MSD在-55 dB左右，其他策略的MSD均高于CCRA策略，节点的平均MSD如表1所示。

图3 网络平均MSD性能对比图

图4 各节点稳定状态MSD性能对比图

表1 稳定状态下的平均MSD对比 dB

DLMS和NDLMS策略和标准的扩散策略的通信负载相同，RC-DLMS和CCRA策略降低通信量的方式是不同，RC-DLMS是降低数据包个数而CCRA是降低单个数据包的长度。为便于比较，用所需通信数据向量的总维数来描述通信负载。无合作LMS中节点不与其他节点通信不作考虑，4种策略的通信负载随时间的比较如表2所示。

表2 4种策略的通信负载对比(CCRA) %

DLMS和NDLMS的扩散策略单位时刻需要传送12 800维信息，而RC-DLMS需要传输6 400维数据，即50%的通信负载下，在收敛速度和MSD性能上接近DLMS和NDLMS。本文提出的CCRA策略在仿真中只需要传输4 800维数据，收敛速度优于DLMS策略和NDLMS策略，MSD性能优于这2种标准策略。针对稀疏参数的估计，本文提出的CCRA策略仅传输压缩后的估计信息，在不影响网络估计性能的情况下，显著降低了WSN所需的通信负载，其中CCRA策略对网络的收敛速度和MSD性能有所改善。

5 结束语

本文给出了WSN参数估计问题的数学模型。介绍了集中式LMS策略和分布式LMS策略的优劣，指出WSN中更适用与分布式策略。针对大多数应用中所估计的未知参数是稀疏的这一特点，提出了一种用于WSN稀疏参数估计的低功耗稀疏参数估计策略CCRA，给出该策略的全局状态空间模型，并证明了CCRA策略的收敛性。仿真结果表明，目标未知参数是稀疏参数时，CCRA策略在不影响网络估计性能的情况下，与其他低负载策略相比，降低了通信负载。