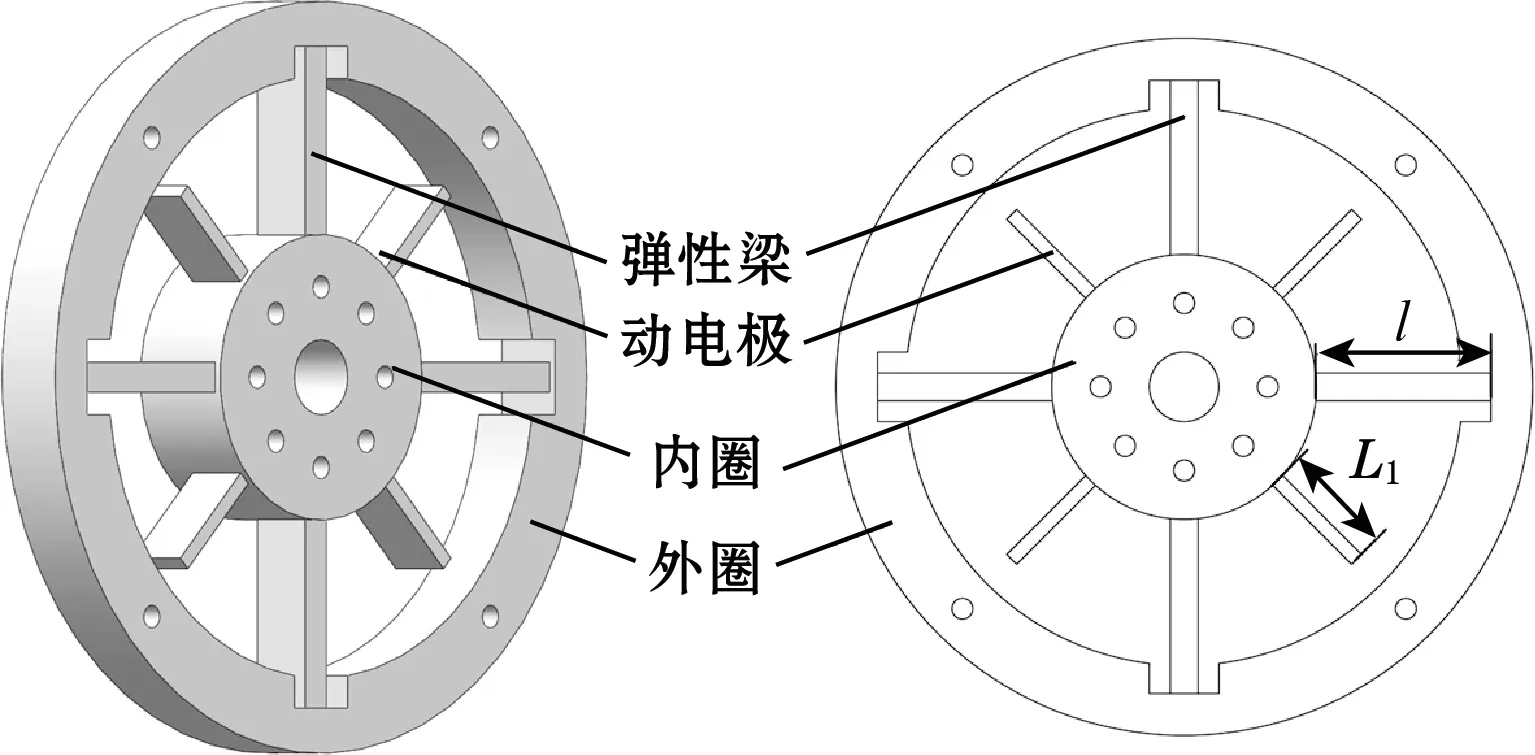
一种十字型双直梁电容式扭矩传感器设计
2022-05-31蒲明辉骆照阳蔡宝成
蒲明辉,骆照阳,蔡宝成,苏 飞
(1.广西大学机械工程学院,广西南宁 530004;2.广西大学广西制造系统与先进制造技术重点实验室,广西南宁 530004;3.湖南科技大学智能制造研究院,湖南湘潭 411201)
0 引言
扭矩传感器能够实时检测扭矩信息,在航空航天、工程机械、电机控制、交通运输和机器人等领域广泛应用[1]。弹性梁作为扭矩传感器的敏感元件,其结构尺寸是影响传感器性能的重要因素[2]。
十字梁作为一种典型的弹性梁结构,国内外对其进行了大量的研究,并取得了一定的成果。盖海松等[3]提出一种十字型轮辐式扭矩传感器,其结构设计简单,易于加工;綦黎明等[4]通过对十字型单直梁进行有限元优化,减小梁的径向宽度提高灵敏度,同时增加弹性梁轴向厚度用于补偿因径向宽度所降低的抗串扰能力;王云燕等[5]设计了一种应变式十字梁海流传感器,通过对弹性梁的长宽高在单因素分析后进行正交试验优化,提高了传感器的测量范围和测量精度。Y. Lou等[6]提出一种带孔的十字梁辐条结构,通过对弹性梁贴应变片处进行打孔产生应力集中,有效地提高了传感器的灵敏度;Y. B. Kim等[7]提出一种十字梯形梁电容式扭矩传感器,通过铁木辛柯梁理论进行分析,确定了扭矩和电容的映射关系。十字梁结构不仅应用于扭矩传感器,在多维力传感器中也被众多学者所研究。孙世政等[8]基于FBG设计了一种十字梁结构的二维力传感器,通过简支梁弯曲变形理论与有限元法在弹性梁最佳位置对光纤光栅进行封装。韩康等[9]针对六维力传感器,通过减少十字型结构弹性梁在应变片黏贴位置的刚度来提高传感器灵敏度。十字梁结构研究虽然较多,但应用于电容式扭矩传感器的研究较少。与应变式[10]和光电式[11]略有不同,电容式要求增大弹性梁两端相对位移来增大动电极位移,从而提高灵敏度,而不是主要关注封装转换元件处的应变。
本文在传统十字梁结构基础上应用铁木辛柯梁理论,建立动极板位移与扭矩的映射关系,分析影响传感器灵敏度和串扰误差的主要参数,提出弹性梁采用十字型双直梁的方案;传感器转换元件采用垂直极板多电容器差动布局,通过对各个通道所检测到的电容乘以比例因子后再进行多电容冗余差动式输出,提高传感器抗串扰性能,串扰是指除轴向扭矩之外的倾覆载荷导致的扭矩传感器测量结果失真[12]。最后通过实验验证了传感器的性能。
1 电容式扭矩传感器灵敏度分析
扭矩传感器转换元件采用垂直极板电容器[13],能够在电极间距变化较小时提供较大的电容改变量,其动、静电极在空间垂直布置,如图1所示。

图1 垂直极板原理示意图
电极间电容值和电极间距的数学关系式[14]为
(1)
式中:C为两电极间电容值,pF;h为两电极之间距离,mm;H为静电极长度,mm;W为静电极宽度,mm;ε为电容介电常数。
由式(1)可以得出,当电极间距发生变化时的电容值变化量ΔC,进行泰勒展开后省略掉二次项:
(2)
式中:h0为电极初始距离;Δh为电极间距变化值。
根据式(2)可知,扭矩传感器的垂直极板电容器对扭矩的灵敏度Ko为
(3)
由式(3)可知,对扭矩传感器内圈施加扭矩时,电容器极板间距变化量和灵敏度成正比例关系,极板间距变化越大,电容器的灵敏度越高。
2 弹性梁结构力学分析
2.1 传统十字型单直梁结构力学分析
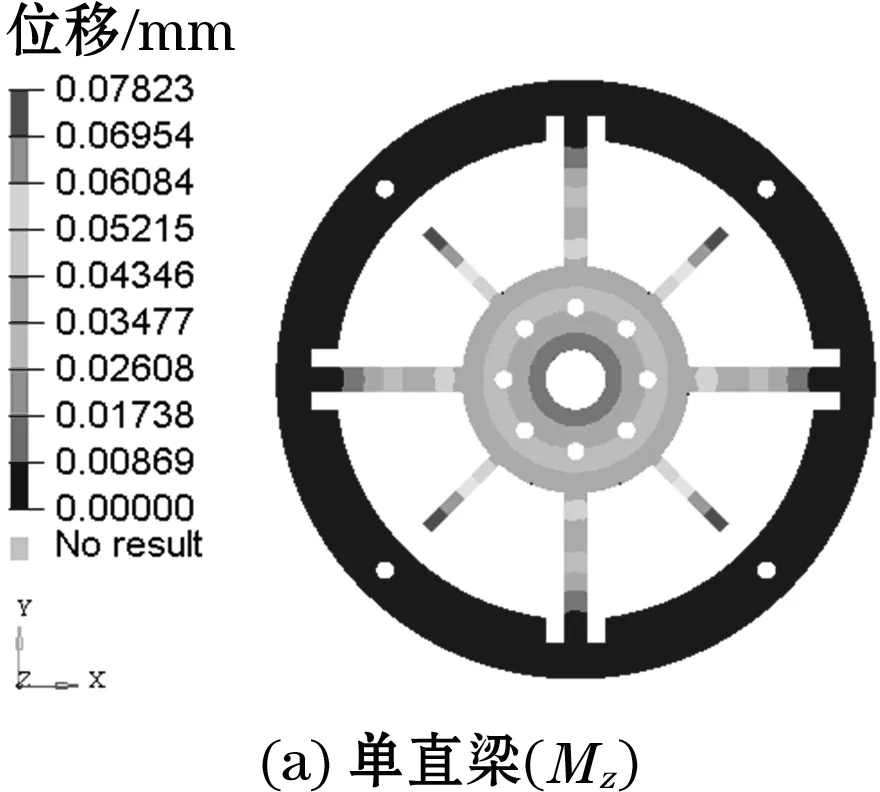
扭矩传感器的十字型单直梁结构及力学模型如图2所示。应用铁木辛柯梁理论对其进行力学分析,当Mz作用于传感器内圈时,外圈作为固定端约束,弹性梁受到反作用力M11和F11共同作用发生形变,内圈因弹性梁形变相对于外圈产生角位移,受力模型如图2(b)所示。
(a)十字型单直梁结构
对单根弹性梁分析,建立力矩平衡方程为
F11l+M11=Mz/n
(4)
式中:l为弹性梁长度,mm;n为弹性梁根数,n=4。
由叠加原则可知,在F11和M11共同作用下弹性梁末端挠度位移y1和转角θl分别为:
(5)
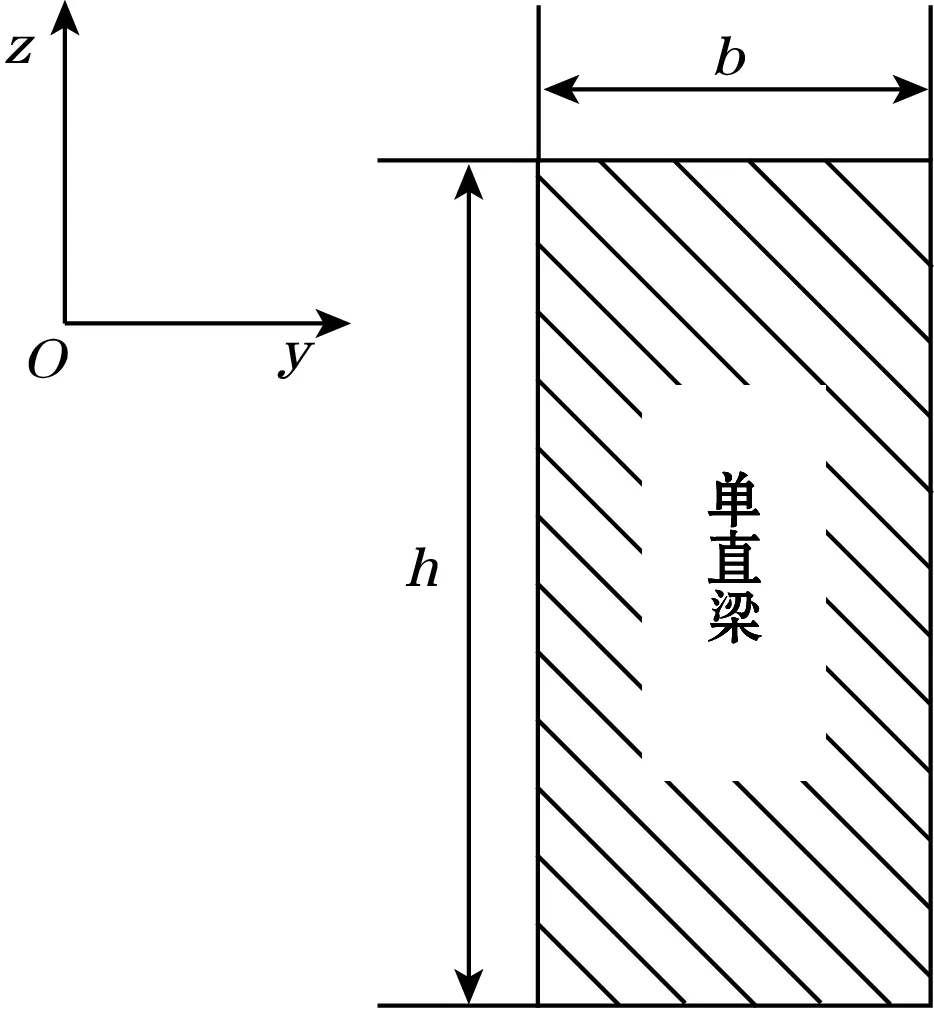
式中:E为弹性梁所选材料的弹性模量;Iz为弹性梁截面对Z方向中性轴的惯性矩;Iz=hb3/12,b为弹性梁截面宽度,mm;h为截面高度,mm。
扭矩传感器内圈在扭矩Mz作用下相对外圈产生转角θN,根据变形协调可得θN=θl,内圈位移yN=yl≈θNr,可求出弹性梁末端挠度yl。分析图2(a)、图2(b),可得Mz作用时的动电极末端位移Δh为:
(6)
式中:L1为动极板长度;r为扭矩传感器内圈半径。
十字型梁结构关于X、Y轴完全对称,故本文在进行扭矩传感器抗串扰能力分析时,仅分析加载扭矩Mx工况即可。当倾覆载荷Mx作用于传感器内圈时,如图2(c)所示,X方向弹性梁绕X轴扭转,Y方向弹性梁末端产生位移,Q(q)点位移垂直纸面向里。结合图2(a)可以看出,动电极末端角位移和X、Y方向弹性梁所产生的角位移θmx相等,则Mx作用时的动电极末端位移Δhp为
Δhp=Hdθmxcosθd
(7)
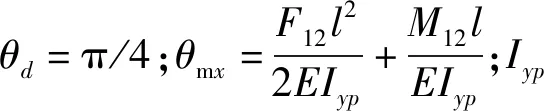
综合分析式(3)、式(6)可知,增加灵敏度的方式主要有:通过减小弹性梁截面的长或宽来降低截面惯性矩Iz;增加弹性梁长度。另外,据式(7)可知,减小弹性梁截面的长或宽会降低Iyp,与增加弹性梁长度一样会使偏载Mx作用下动电极位移增大,导致测量值有一定程度的失真,降低了传感器的抗串扰能力。
2.2 十字型双直梁结构弹性梁设计分析
通过对十字型单直梁模型进行理论分析可知,为在增加灵敏度的同时,尽量不影响传感器的抗串扰能力和厚度,可在不改变弹性梁截面对Y轴惯性矩的前提下,仅降低弹性梁在Z轴扭转方向的抗弯刚度。将单直梁结构弹性梁在传感器径向方向沿中线分割,使中间位置产生较小间隙的方式来降低弹性梁在Z轴扭转方向的抗弯刚度。改进后的十字型双直梁结构与单直梁结构的弹性梁截面尺寸对比如图3(a)、图3(b)所示,传感器整体结构如图3(c)所示,图3(d)为力学建模。
(a)弹性梁截面(单直梁)
根据图3(b)所示,由负面积法可得到双直梁结构弹性梁截面对Y轴惯性矩Iys为
(8)
由式(8)可知,改进后双直梁传感器模型弹性梁截面对Y轴惯性矩与单直梁模型相等。
对双直梁结构施加扭矩Mz时,为使模型易于计算,将与弹性梁连接的内圈部分简化为与弹性梁截面相同的固接杆CD,最终建模为截面面积相同的三次超静定桁架结构。对末端施加力F,去除B点约束,以支座反力X1、X2、X3代替,如图3(d)所示,三次超静定协调方程为:
(9)
式中:Xk为支座反力;δij为在Xi作用下Xj产生的挠度;ΔmF为Xm作用下F产生的挠度(i,j,k,m=1,2,3)。
采用图乘法分别对式(9)中的参数进行计算后,可分别求出在F、X1、X2、X3单独作用下,弹性梁末端的挠度ΔF、Δx1、Δx2、Δx3为:
(10)
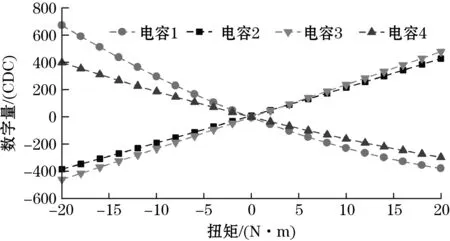
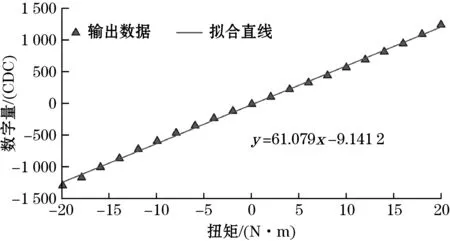
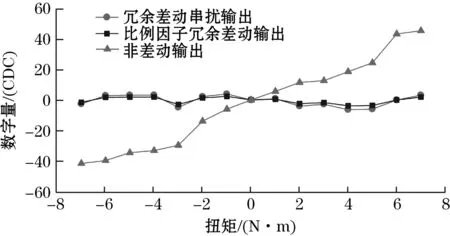
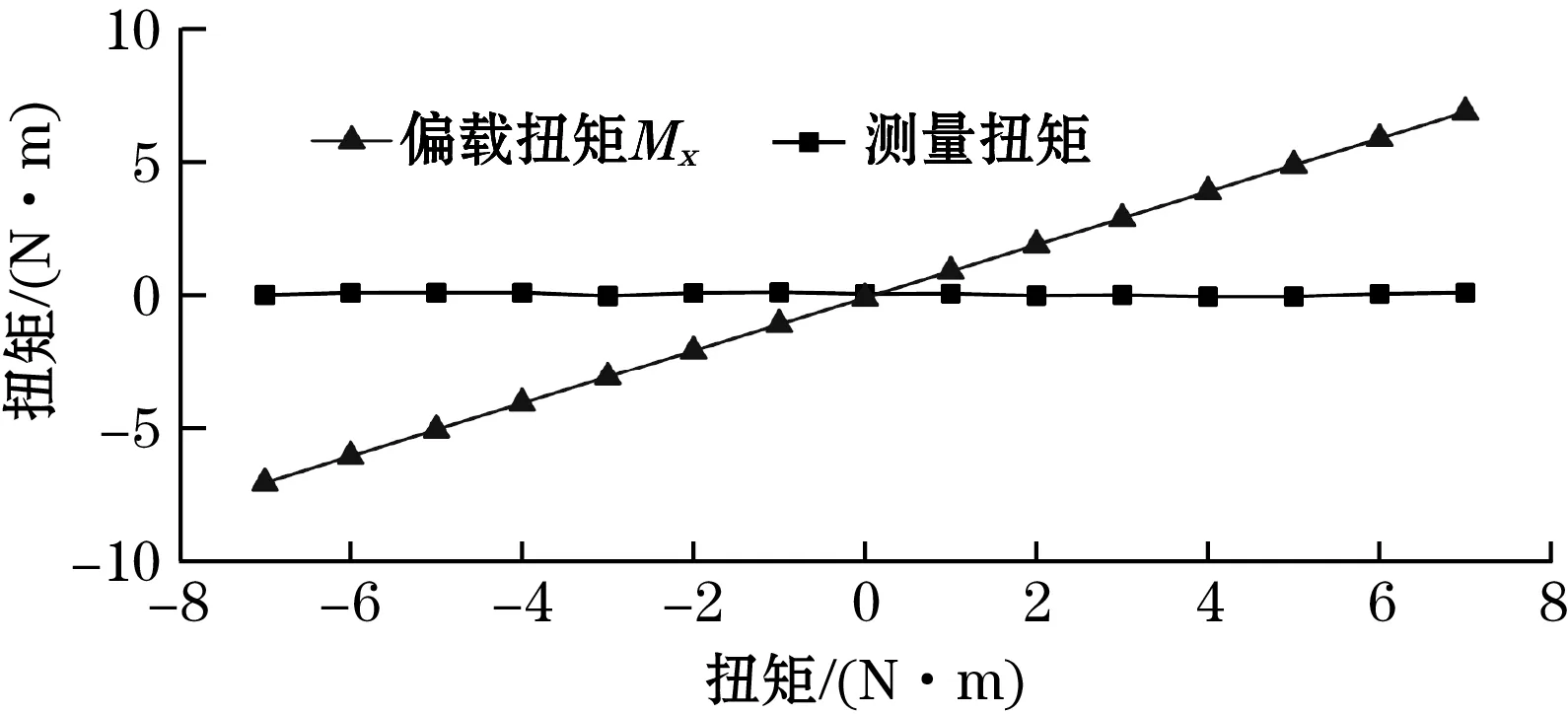
由式(10)可得,当b< (11) 根据式(5)、式(11)可得,对十字型单直梁和双直梁弹性梁末端分别加载数值相同的力F,其末端位移比值Kf为 (12) 对2种传感器模型内圈加载扭矩Mz,弹性梁末端同样受到反作用力M和F。根据式(5)可知,在F和M分别作用下的弹性梁末端位移成比例关系,因此对传感器加载Mz时,其末端位移比值与单独加载力F相等。由式(3)可知,扭矩传感器弹性梁末端位移与灵敏度成正比例关系,因此受到扭矩后,2种模型弹性梁末端位移的比值与灵敏度比值相等。据式(12)可知,所优化后的双直梁模型相比于单直梁其灵敏度提高了约(4b+1)/8倍。 扭矩传感器对称安装了4个垂直电极电容器,电容器分别位于电路板的相对两侧,构成冗余差动式结构,如图4所示。对传感器施加顺时针方向扭矩,C1和C3电极间距减小,电容增加一个非线性的电容值;C2和C4电极间距增大,电容减小一个非线性的电容值。因为存在极板安装误差等影响因素,4个电容器在满载时的最大变化值是不同的,为将电容器输出调整一致,需要对每个电容的变化值乘以一个比例系数。因此,扭矩传感器电容输出可由式(13)表示: 图4 冗余差动式电容器布置示意图 (13) 式中:比例系数Ki=ΔCmax/ΔCi max;ΔCi为第i个电容器在传感器受载后相应的电容值;ΔCmax为传感器标定至满载时,4个电容器中变化量最大的电容值;ΔCi max为第i个电容器在传感器标定至满载时电容值。 扭矩传感器机械本体采用2A12硬铝合金制作,弹性梁参数如表1所示。电容测量采用电容-数字转换芯片AD7147,具有16位分辨率,能够将所检测到的电容值(pF)转化为数字量(CDC),对PCB板制作并进行安装,传感器整体如图5所示。搭建电容式扭矩传感器标定系统如图6所示,主要包括扭矩传感器、标定平台、AD7147评估板、上位机。标定平台包括加载法兰、固定台等。 表1 扭矩传感器弹性梁参数 mm 图5 十字型双直梁扭矩传感器示意图 图6 标定系统意图 为验证双直梁结构力学模型准确性,采用表1所示的参数分别建立除弹性梁之外其余部分完全相同的十字型单直梁和双直梁简化模型。图7(a)、(b)分别为2种模型受Mz=20 N·m时的位移云图,图7(c)、(d)分别为2种模型受扭矩Mx=7 N·m时的位移云图。 2种工况(Mz、Mx)下单直梁和双直梁结构动电极末端位移比的理论值可分别由式(8)、(12)分析得出,有限元仿真中扭矩加载数值、动电极位移比的仿真值及理论值见表2。 图7 扭矩传感器仿真示意图 表2 扭矩传感器动电极位移 分析表2可知,对2种模型分别加载Mx,电极位移比的仿真值和理论值近乎相等,因此其具有相同的抗串扰能力。加载Mz时,结合式(3)得,双直梁结构扭矩传感器相比于单直梁,其灵敏度提高了1.774倍。但是电极末端位移比的理论值略高于分析仿真值,造成上述现象的主要原因如下: (1)对双直梁模型加载Mz,为了满足图乘法的使用条件,在力学建模时将CD简化为和AC、BD段具有相同抗弯刚度的弹性梁。所建双直梁模型的整体刚度小于真实值,电极位移比理论计算值偏大。 (2)计算双直梁模型弹性梁末端位移时,如式(11)所示,为了减少计算复杂度,采取假设条件b< 基于以上弹性梁结构的理论及有限元分析,设计制造电容式扭矩传感器,并对其进行标定,在标定过程中,4个电容器电容值会被模数转换芯片AD7147同时检测,并通过芯片中的4个数据传输通道转变为相应的数字量输出。以输入扭矩为横轴,以AD7147所检测到的数字量输出为纵轴,标定所得冗余差动结构4个电容的变化如图8所示。 图8 冗余差动结构电容器变化值拟合曲线 扭矩传感器输出以式(13)方式对图8所示的电容数据进行计算得出,并采用最小二乘法进行线性拟合如图9所示,传感器的性能参数如表3所示。 图9 扭矩传感器输出特性直线 表3 传感器性能参数 对传感器施加量程为7 Nm的Mx干扰扭矩,步长为1 Nm,分别测得4个电容器的电容变化值。图10为对4个电容变化值进行非差动、冗余差动和式(13)所示的添加比例因子冗余差动3种方式得出的串扰输出曲线。通过图10可以看出带有比例因子的多电容冗余差动设计有效地提高了扭矩传感器抗串扰能力。 图10 冗余差动与非差动式串扰输出对比 图11所示为扭矩传感器在受到7 N·m的Mx干扰扭矩时实际测量的情况,对图11的数据进行计算可知,传感器的最大串扰误差为1.52%FS,小于文献[12]中的4.9%FS。结果表明,该传感器具有较强的抗串扰能力。 图11 偏载扭矩与测量扭矩对比 本文通过对十字型单直梁结构中影响灵敏度和抗串扰能力的参数进行理论分析,设计一种十字型双直梁结构电容式扭矩传感器,通过有限元分析和对传感器实物标定实验验证,结论如下: (1) 本文所设计的十字型双直梁结构扭矩传感器与参数相同的单直梁结构传感器相比,在未减弱其抗串扰能力的前提下,将灵敏度提高了1.774倍。通过标定实验得到灵敏度为63.38CDC/(N·m),线性度为2.15%FS,迟滞为1.4%FS。 (2)电容式扭矩传感器的检测方案采用冗余差动式布置时,在输出之前,对各个通道电容值添加比例因子,相比于非差动输出、冗余差动式直接输出,可以将传感器的抗串扰能力进一步提高。通过抗串扰实验得出扭矩传感器的串扰误差为1.52%FS。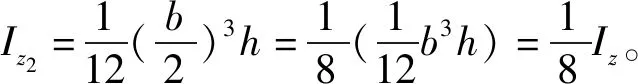
3 双直梁电容扭矩传感器设计及标定
3.1 多电容冗余差动式检测方案设计与分析

3.2 扭矩传感器制作及标定系统介绍



4 结果与分析
4.1 弹性梁仿真结果对比分析

4.2 扭矩传感器性能分析

4.3 扭矩传感器抗串扰能力分析
5 结束语
