四类预测人口方法的对比及Logistic人口生长模型的改进
2022-05-31王沛林
王沛林
(北京理工大学 数学与统计学院,北京 100081)
在当今科技经济飞速发展的社会中,人口问题一直是世界各个国家和各个领域所关注的焦点问题,它是一个社会发展的最基础也是最关键的问题.为了维持社会生活的基本平衡与稳定,把人口数量保持在一个比较理想化的状态,就要对国家和地区的人口总数进行合理预测,以便制定未来人口政策,使社会有序发展.在早期的研究中,进行人口定量预测的基础方法就是依据国家统计局的人口结构和规模的资料和数据,以当前人口为出发点,并且对未来人口的变化趋势作出合乎常理的假设,运用科学的数学模型进行拟合演算,进而预测出未来人口总数、性别比例、结构组成等一些重要人口要素.
社会的进步需要人口稳定可持续发展,基于中国人口数量现状和上述已知方法,本文通过比较马尔萨斯人口模型、多项式拟合模型、ARIMA模型和Logistic人口生长模型的预测效果,着眼于未来人口总数的估计分析,关注人口发展的总体趋势,并将现有Logistic人口生长模型从微分方程和模型参数拟合优化角度进行改进,得到了更加准确的预测方程,以便更好地预测今后一段时间中国的总人口数,具有一定的预见性.
1 中国人口发展预测模型的建立
1.1 数据的选取
拟合数据的选取十分重要.经过资料调查,我们知道从20世纪70年代,在全国范围内开始大力实施计划生育政策[1],所以在预测全国总人口时,我们选取1970年为基础年份,1970年的总人口数量为最初人数.进而考虑到数据选取的原则,数据选择得越多,即样本越多,能准确预测拟合人口数量的可能性越大,结果就越精确,误差就越小,所以选择的年份不能少于25年,否则将很难发现人口数量变动的趋势.再有,我国自2016年1月1日起,正式开始实行“全面二孩”政策[2],这项政策的实施在短期内不会对我国总人口数的变化趋势产生较大的影响.因此,在本文中先不考虑近几年二胎方针的影响.最后通过查阅中国国家统计局网站,获得1970—2014年每年中国人口总数,以这45年的数据作为拟合数据,保证了一定的准确性.
1.2 模型假设
1)现有的基本国策“计划生育”保持不变.
2)不考虑战争等不可预见因素.
3)由于环境等因素,人口不能无限制地增长.
1.3 马尔萨斯人口模型及其应用
1.3.1 模型的理论背景
人口学家马尔萨斯在生物增长定律中提到:人口的变化率与人口总数成正比[3],且这个比率不随时间变化,为常量.由此,我们设定人口总数为p(t),人口变化率为l,若已经知道在t0时刻的人口数量值p0,则就可以得到马尔萨斯人口模型:

这就是非常著名的分析人口数量问题的基础微分方程模型,通过求解方程,我们可以得到它的另外一种表达形式:

其中,t0表示最开始的时间(即初始年份),p0表示t0时刻的人口总数,t表示一般意义上的时间,p(t)表示t时刻的人口总数.
1.3.2 模型的建立与实现
将1970—2014年每一年的人口总数作为基础数据,代入模型中.为了进行数据拟合,首先要考虑模型的求解实现问题.
参数估计:l、p0可以用已知数据,运用线性最小二乘法进行估计.(2)式两边取对数,得到:

作对数变换后,再以1970—2014年的人口数据拟合(3)式,经计算得到:l=0.011 2,p0=88 521.43.
最后,得到马尔萨斯人口模型:

其中t0=1970.
得到模型的表达式以后,我们进而对2015—2019年的人口进行预测.
1.3.3 模型的误差检验分析
评价一个模型的好坏以及拟合效果,首先可以通过实际值和拟合值作出的图像来直观地对比分析.
如图1所示,在马尔萨斯人口模型预测图中,这45年来实际人口和预测人口的总体增长趋势大体是一致的,但是到后期预测人口的增长率要明显大于实际人口的增长率.

图1 马尔萨斯人口模型预测1970—2014年总人口
通过计算误差来进一步分析模型的优劣.在统计学中,我们惯用yi来代表第i组数据的真实值,来代表第i组数据的预测值,用n来表示样本数据的组数,所以有误差指标为:相对误差(RE),残差平方和(resnorm):,标准误差(RMSE):
相对误差越小,模型可信度越高;残差平方和越小,模型拟合效果越好;标准误差越小,模型精密度越高;Rnew为非线性回归方程的拟合优度指标,其值越靠近1,模型拟合程度越高[4].
知悉这几个误差指标后,用Matlab计算出由马尔萨斯人口模型拟合的这45年数据的相对误差最大值为0.066 6,残差平方和为4.941 7,标准误差为0.331 4,Rnew为0.971 3.
在物理学中,一般相对误差不超过5%算是比较精确[5],但此模型最大相对误差0.066 6要高于0.05,并且Rnew的值离1还有一定距离,由此看来马尔萨斯人口模型的精确度不是很高.
1.3.4 模型的预测效果及总体评价
将前文利用马尔萨斯人口模型预测出的2015—2019年中国总人口数与国家统计局网站上的真实数据进行对比,以此来判断预测效果.
由表1可以计算出,这5年的相对误差最大值为0.094 6,远大于0.05,误差较大,预测效果并不是很理想.

表1 中国2015—2019年实际总人口数与预测总人口数 万人
进一步绘制2015—2030年的人口预测图,从图2中可以看出预测人口的年增长率过高,人口数量呈几何状增长,不太符合实际.

图2 马尔萨斯人口模型预测2015—2030年总人口
从马尔萨斯人口模型的拟合效果和预测结果来看,计算出来的误差较大,模型并不是很精确,其预测的人口数量呈指数增长,增长率过高,故该模型的现代利用价值有限.
1.4 多项式拟合模型及其应用
1.4.1 模型的理论背景
从图1中我们可以观察出,人口数量的变化过程线上各点斜率都不太相同,这就表明各个阶段的人口增长速率是不一样的,这时用单纯的一条直线来描绘人口的发展显然是不合适的,所以要用更贴近实际的曲线来拟合人口数量的变动,这就产生了多项式拟合模型.
1.4.2 模型的建立与实现
为了保证多项式拟合模型的合理性和准确性,并且兼顾误差最小的原则,还要使模型具有可解释性,故本文选取了三次多项式对1970—2014年的总人口数据进行拟合.
将时间t作为解释变量,中国总人口数量p(t)作为预测变量,建立多项式确定它们之间的关系.得出如下结果:

1.4.3 模型的误差检验分析
通过图3拟合图像可以看出,在1970—2014年中,拟合的曲线很贴近实际的数据,三次多项式拟合模型的短期预测效果很好,没有太大的误差.

图3 三次多项式拟合模型预测1970—2014年总人口
三次多项式的相对误差最大值为0.0133,残差平方和为0.122 3,标准误差为0.052 1,Rnew为0.995 5.由误差可以看出,多项式拟合模型的精确度较马尔萨斯人口模型有很大程度的提高.
1.4.4 模型的预测效果及总体评价
利用三次多项式拟合模型的表达式,预测出2015—2019年中国人口总数分别为136 090万人、136 194万人、136 218万人、136 161万人、136 021万人,将这5年来的预测人口同实际人口相比较,我们得出最大的相对误差值为0.028 5,没有超过0.05,且要远低于马尔萨斯人口模型的误差值,预测效果比较好.
从三次多项式拟合模型的曲线贴合效果和部分预测结果来看,各种误差都比较小,模型比较合理,但是2015—2019年预测出来的人口数量总体呈现先增长后下降的趋势,人口数量下降在我国现阶段几乎是不可能的,所以笔者认为多项式拟合模型只适合短时段1~3年内的人口预测,长期预测则会出现大的偏差,效果不会很好.
1.5 ARIMA模型及其应用
1.5.1 模型的理论背景
由前面的多项式拟合模型可以看出,人口数量是随着时间不断变化的.但是人口与时间的关系又不能简单地用多项式来准确的描述,为了寻找更合理的人口预测模型,我们想到了经济学中的ARIMA模型.
预测一种事物的变化时,用它的过去推断它的未来,即用时间序列的往日数据表示事物随时间变化的种种规律,并将两者之间的模式应用到未来,进而对未来的数据作出预测.ARIMA模型就是一种常用的时间序列模型.
ARIMA(p,d,q)模型含有 3个参数,这里面 p表示自回归(AR)阶数,q表示移动平均(MA)阶数,d 表示模型的差分阶数[6].该模型有 3 种基本类别[7]:AR(p)模型、MA(q)模型、ARIMA(p,d,q)模型.
1.5.2 模型的建立与实现
利用1970—2014年的中国总人口数据,建立ARIMA(p,d,q)模型.模型的建立步骤如下:
1)载入数据,进行一次单位根检验,判定数据序列的平稳性.本文得到p值为0.99,大于检验的临界值0.05,所以该序列不平稳.
2)对不平稳序列进行差分处理,差分的次数为d,使其成为平稳序列.经过了三次差分操作后,一次单位根检验的p值小于了0.05,序列化为平稳序列,进而确定d=3.
3)对已经平稳的序列进行白噪声检验,判断其是否为纯粹的随机序列,由于对白噪声进行下一步的处理和预测没有任何价值,故使用Ljung-Box方法[8]进行检测.p值为0.008 808,小于标准值0.05[8],所以三次差分后的平稳序列不是随机序列,可以展开下一步工作.
4)确定模型的阶数.画出序列的自相关图(ACF)和偏自相关图(PACF),见图4.据观察可以发现ACF 1阶截尾,PACF具有拖尾性.综上,初定模型为ARIMA(0,3,1).接下来用R语言软件中的自动定阶功能(auto.arima)来对上面的定阶结果进行准确性检验,结果也显示为ARIMA(0,3,1)模型.

图4 自相关图与偏自相关图
5)确定模型的系数.得出该模型为xt=εt+0.769εt-1.
6)模型的显著性检验.使用Ljung-Box方法[8]检验残差:p 值为 0.287 8,大于 0.05,说明残差是随机序列,白噪声检验通过.参数的显著性检验:用R软件测出的系数-0.769 0除
以它的标准误差0.122 7,商的绝对值为1.96,大于T检验统计量在5%水平的临界值,断定系数显著不等于零[9],检验通过.
7)用 ARIMA(0,3,1)模型预测 2015—2019年的中国人口总数.
1.5.3 模型的误差检验分析
从图5可以看出,ARIMA模型作出的预测数据与实际数据比较吻合,相差不大,效果良好.

图5 ARIMA模型预测1970—2014年总人口
相对误差最大值为0.003 3,残差平方和为0.006 3,标准误差为0.011 8,Rnew为0.999 0.从误差值来看,模型的拟合水平非常高,较前面2种模型而言,有着更高的可信度.
1.5.4 模型的预测效果及总体评价
利用ARIMA模型预测2015—2019年的中国人口总数,将预测值与实际值作比较,得出相对误差的最大值为0.002 8,远小于前2种模型的误差值,预测效果有了质的飞跃.
进而利用此模型预测出了2015—2030年中国的总人口数,并绘成图6.看出未来10年我国人口将呈缓慢增长态势,到2030年不会破15亿大关.

图6 ARIMA模型预测2015—2030年总人口
根据综上各种论证来看,ARIMA模型的预测效果远优于前2种模型,给出了较为合理的人口随时间变化的趋势,精确度比较高,有较大的参考价值.
1.6 Logistic人口生长模型及其应用
1.6.1 模型的理论背景
在前面讨论过的马尔萨斯人口模型中有致命的缺点——人口变化率l为常量.它只假设出了人类发展最理想的情况,并得出人口数量将呈指数上涨的极端结论.认识到马尔萨斯人口模型的不足之后,有学者在其基础上进行了改进,形成了Logistic人口生长模型.模型的中心观点为:人口数量并不能无穷尽地上涨,它会受到各种因素的约束,且随着人口的不断增加,这种约束力会不断变强,最终人数会到达一个极值.

1.6.2 模型的建立与实现
从上述的理论基础中可知,如果想获取方程(10)的解,就要估计出pm和l这2个参数的值,求解方法有2种.
1.6.2.1 三点等间距法
利用昔日的人口数据,粗略计算出l和pm的值.再采用t0、t1、t2这3个年份的人口总数量p0、p1、p2,且满足条件t2-t1=t1-t0=a,代入方程式(10)进行计算,可得出:

取1970年作为开端年份t0,取1992年为中间年份t1,取2014年为最末年份t2,此时a=22,将相应数值代入公式(11),获取l和pm的具体值;将计算出的2个参数值代入方程(10)中,得到模型,模拟图见图7.
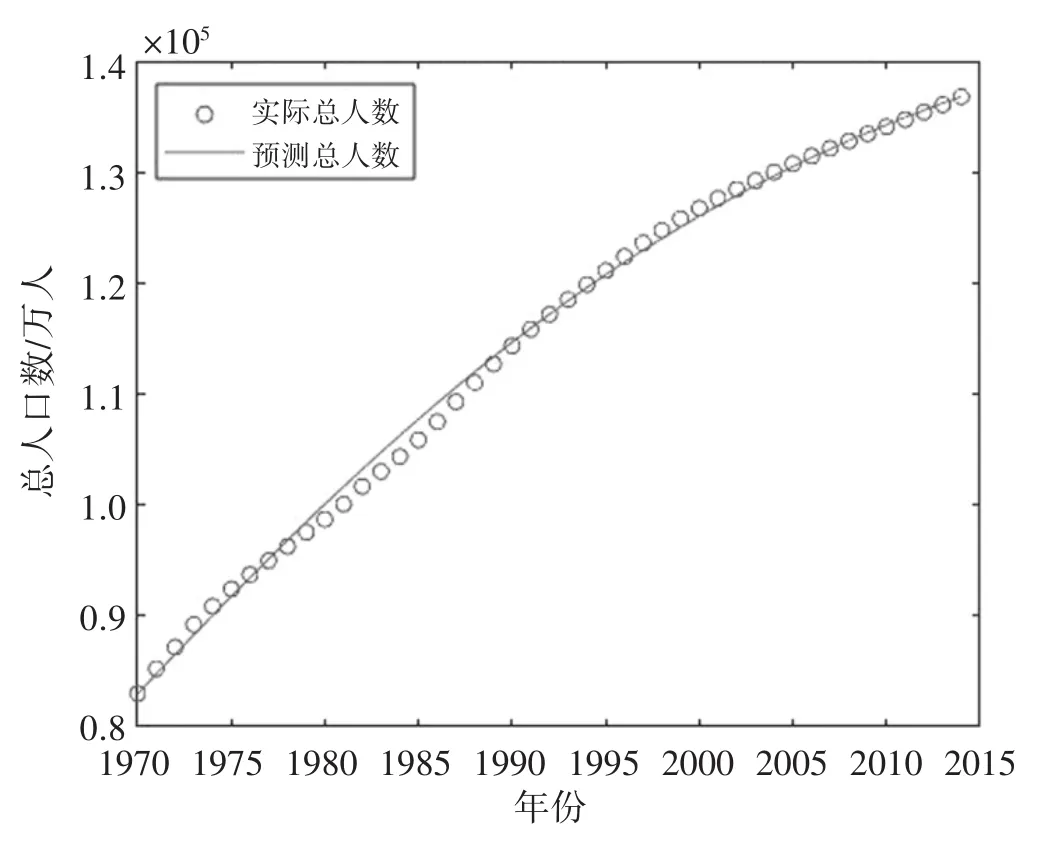
图7 Logistic模型三点等间距法预测1970—2014年总人口
1.6.2.2 lsqcurvefit最小二乘法
在Matlab软件中有一个lsqcurvefit命令,依据最小二乘原理即使模拟数据和实际数据之间的残差平方和最小,也可拟合出最优化的非线性曲线.
选取 t0=1970,p0=82 992代入式(10),然后将式(10)作为未知的需要拟合的非线性曲线,l和pm为要求解的参数.给出两参数的初值解,1970—2014年的总人口为实际数据,用lsqcurvefit函数进行拟合,pm为153 147 万人,l为 0.045 4,有模型,最后画出对比图,见图8.

图8 Logistic模型最小二乘法预测1970—2014年总人口
1.6.3 模型的误差检验分析
从图7、图8中可以剖析出,三点等间距法和最小二乘法的模拟结果都不错.
三点等间距法:相对误差最大值为0.018 2,残差平方和为0.305 0,标准误差为0.082 3,Rnew为0.992 9.最小二乘法:相对误差最大值为0.013 5,残差平方和为0.247 7,标准误差为 0.074 2,Rnew为 0.993 6.很明显,最小二乘法还是要略优于三点等间距法,这可能是因为lsqcurvefit函数能够找到全局最优解,而三点等间距法只是拿出3年的数据来求解方程(10),有局限性.
1.6.4 模型的预测效果及总体评价
综上,我们选用最优的lsqcurvefit最小二乘法预测出了2015—2019年的总人口数,与实际人口比,最大相对误差值为0.003 9.进而本研究用Logistic人口生长模型预测出了2015—2030年的总人口,见图9.

图9 Logistic人口生长模型预测2015—2030年总人口
从图9可以发现,在未来10年我国人口增长有逐渐放缓的趋势,总体较平稳.
总体来说,Logistic人口生长模型比马尔萨斯人口模型考虑的影响人口变动的因素更多更充分,预测结果也更加确切、合理.但是,从误差的角度来看,该模型还不如ARIMA模型精确,有改进优化的空间.
2 4种预测方法的比较分析
通过表2我们清楚地认识到,无论是从误差最小化角度,还是从模型的拟合效果和预测结果方面,Logistic人口生长模型和ARIMA模型都要优于其他两种模型,并且ARIMA模型的精确性还要比Logistic人口生长模型突出,但是ARIMA模型的局限性在于它只适合短时间内的预测[11],而Logistic人口生长模型作为中长期人口预测的一种典型方法,它的精确度还有待提高.为了更好地进行人口中长期预测,下文将探讨Logistic人口生长模型的改良方法.

表2 4种预测模型的比较分析
3 Logistic人口生长模型的改进
通过分析看出,Logistic人口生长模型在预测人口时,其自身的合理性和精确度还有进一步提升的空间,为此我们从2种不同角度探索对此模型修正的方法.
3.1 方程角度改进及其应用
3.1.1 改进的方法依据
从我国的当前人口形势出发,由于计划生育政策已实行了多年,我国过去人口猛烈增长的势头已经得到了很好的控制,久而久之又出现了生育率低、人口老龄化的现象.如今我国的人口增长率已经非常低,如方程(7)的假设——人口变化率l和人口总数p(t)是最简单的线性关系,已经不再适用于当下.现在我们从l与p(t)的关系入手,对l(p)函数式进行改进.
作出假设:人口上涨已经快到了负荷的程度,上涨率慢慢变小最终将趋向零.
根据假设,l(p)理应表达为e-p的函数,设:

其中l(p0)是初始年份为t0、总人数为p0时的人口增长率,b、k为待求系数.
于是,修正以后的模型为:

3.1.2 模型的建立与实现
依旧使用1970—2014年的中国人口总数作为研究数据,这样上下文形成对照,方便比较拟合效果.先来求解方程(12)中的参数值b、k.
首先,对方程(12)的两边作对数变换得到:

最后,得到从方程角度进行修改后的模型:

其中起始年份t0为1970年.求出了方程(15)的数值解,并绘制拟合图像,见图10.

图10 方程角度改进的Logistic人口生长模型预测1970—2014年总人口
3.1.3 模型的误差检验分析
根据图10可看出,从方程角度改进后的模型绘制的拟合曲线与现实中的数据比较贴近,在开始的5~6年和末尾的5~6年预测效果尤其好,在中间年份或多或少出现了偏差.依据程序运行结果,相对误差最大值是0.026 3,残差平方和是0.796 3,标准误差是0.134 5,Rnew是0.988 4.从误差值的大小来看,此方法修正后的Logistic人口生长模型并没有较大改善.
3.1.4 模型的预测效果及总体评价
与前文一样,我们用改良的模型预测出了2015—2019年的中国人口总数,与实际人口比较,这5年的最大相对误差值为0.004 0,这与没有修正之前的最大相对误差值0.003 9差距非常小,几乎没有改善.之后,用改进后的模型预测了2015—2030年的中国总人口,见图11.
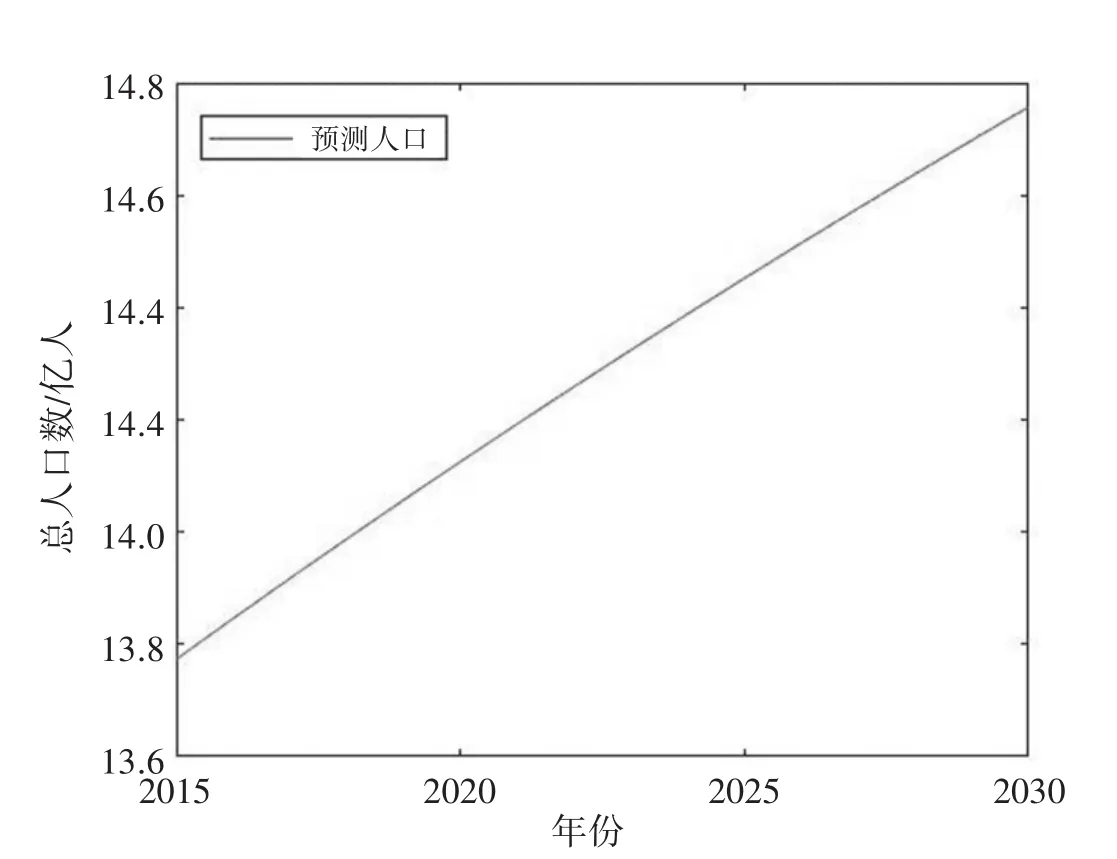
图11 方程角度改进的Logistic人口生长模型预测2015—2030年总人口
将图11与图9对比发现,改进前预测2015—2030年的中国总人口大约是从13.8亿上涨到14.5亿,改进后预测这16年的人口数大约是从13.8亿上涨到14.7亿多,首尾年都相差不大,说明我国未来人口的变化有很大可能按照这种趋势发展,并在2030年达到14.6亿左右的人口数.
无论是从误差指标的角度来看,还是从预测效果来看,修正了主方程的Logistic人口生长模型并没有很大程度上提高模型的效率和精确性,与没修改之前的预测大致相同,借鉴意义有限.
3.2 参数角度的模拟仿真改进及其应用
3.2.1 改进的方法依据
本文又从另一个角度——使参数值更加精确化,来对模型的修正问题进行探究.
在Logistic人口生长模型中,存在关系函数l(p)=l-sp,l>0,s>0,此式中含有2个待求参数l和s.我们知道,这2个参数主要是通过专家预估[10]或者统计得来,而没有从函数式本身入手去求其值.所以,修正模型中l(p)的决定方式,根据1970—2014年逐年的总人口增长率与每年人口总数的关系,运用最小二乘线性拟合的方法来明确参数l、s的切实值,即通过真实数据的模拟仿真来确定参数值,而不是无端的估计统计,这样预测水平可能会有所提高.
3.2.2 模型的建立与实现
应用国家统计局的数据计算出1970—2014年中国总人口的逐年变化率,并制成散点图.
由图12可以观察出,总人口的增长率自1987年开始,几乎呈直线型下降,因此可以采用直线拟合的方式来得出函数l(p)=l-sp,l>0,s>0的具体表达式.
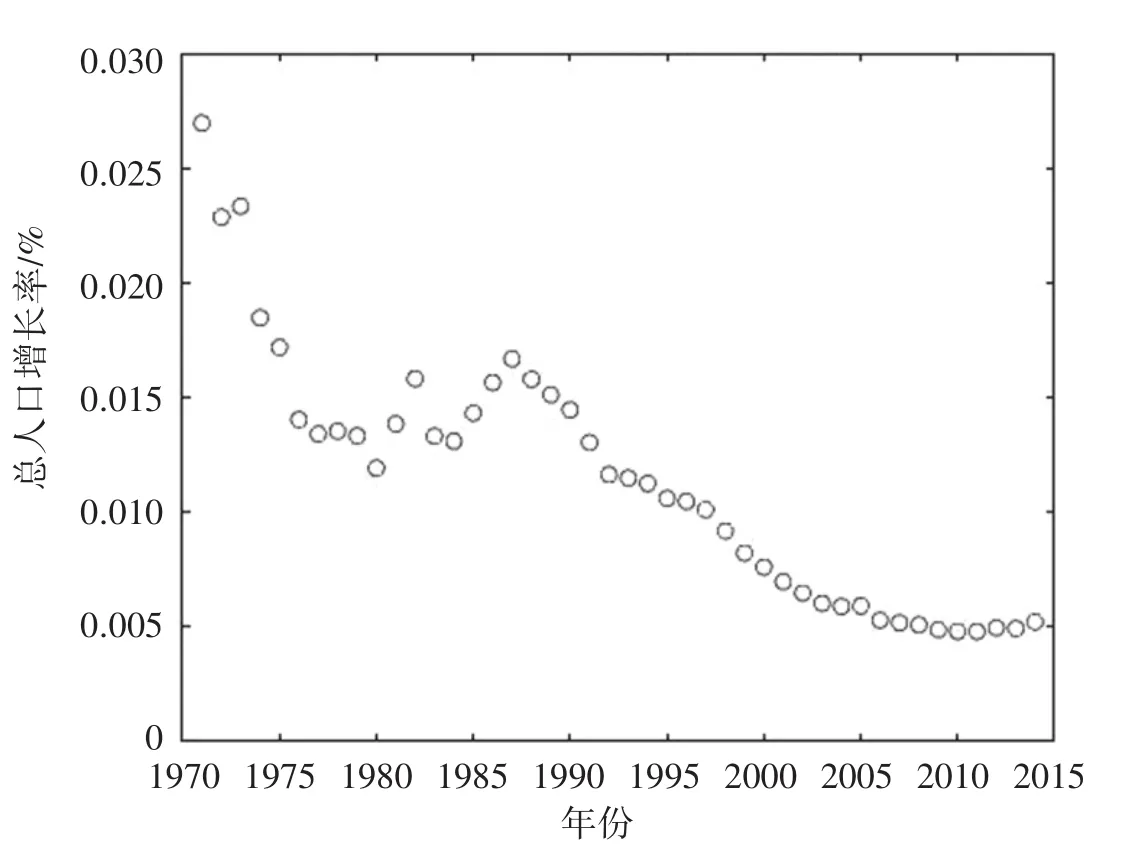
图12 1970—2014年中国总人口的增长率变化
于是,1987—2014年逐年的总人口增长率作为l(p),1987—2014年每年的总人口数为p,运用线性最小二乘法来拟合它们之间的关系式l(p)=l-sp,最终得到具体表达式为:

将1987年当作初始年份t0,1987年所对应的总人口数为p0,2个数值与式(16)一起代入方程(6),得到方程:

而后再求解微分方程(17)得到了预测总人口数p(t)的解析式:
实际总人口与预测总人口相比较,见图13.

图13 参数角度改进的Logistic人口生长模型预测1987—2014年总人口
3.2.3 模型的误差检验分析
查看拟合图13,我们发现改进后的模型作出的预测数据与真实数据很接近,总体的增长趋势也相当一致.
通过计算,得到了该模型下相对误差最大值是0.006 9,残差平方和是0.086 0,标准误差是 0.055 4,Rnew是 0.995 6.改进后模型计算出的误差指标值要比原模型计算出的误差值小得多,拟合优度Rnew也更加接近1,结果良好.
3.2.4 模型的预测效果及总体评价
同样,我们用改良后的模型预测出了2015—2019年的中国总人口数,分别为137 480万人、137 901万人、138 298万人、138 671万人、139 023万人,预测值与实际2015—2019年总人口数的最大相对误差值是0.007 0,与之前未改进时的预测效果相近.接着我们又预测了2015—2030年的中国总人口数,见图14.

图14 参数角度改进的Logistic人口生长模型预测2015—2030年总人口
可以看出,按此种模型进行推测,我国的人口增长率减小的趋势将加快,人口增长将放慢.
利用真实数据对未知函数进行模拟仿真,进而求解出更加有实际意义的参数值,这种改进方法经过实践证明具有不错的效果,使模型的拟合优度有了较大提高,从误差值来看也比原始模型更具有说服力,精确性大幅度提高.
3.3 模型的改进效果剖析
无论是从模型存在的偏差还是从模型的拟合优度指标来看,从参数角度进行的模拟仿真改进远远要比从方程入手对模型的改进效果理想得多.改进后的模型,参数值被赋予了更加具体的内涵而且也精确了许多,同时,与原有的Logistic人口生长模型相比,从参数角度改进后的模型精确度提高了,预测水平也升高了.
本文通过比较马尔萨斯人口模型、多项式拟合模型、ARIMA模型、Logistic人口生长模型这4种人口预测方法的优劣,认为ARIMA模型和Logistic人口生长模型的预测效果比较理想,并用比较合理的Logistic人口生长模型对未来的人口进行了预测,进一步针对Logistic人口生长模型存在的不足提出了2种改进办法,使模型的精确度进一步提高.最后预测,到2030年,我国的总人口将在14.2亿~14.6亿波动.
