综合实践表现性评价设计案例

廖健珍

前言：

学习效果如何，需要通过评价来体现。量化评价和质性评价是两种常用的评价，而在课程改革的推进过程，学习评价始终是一块“软肋”，也是一块“硬骨头”。就小学数学评价现状而言，主要还是依据考试成绩，但如果总是停留在简单的结果对错判定上，那么对学生的数学理解、数学表达、数学思考等综合学习能力与素养的评价则会相对欠缺。因此表现性评价则会将这些内隐性比较强的思维和能力，通过一定的形式将其“外显”，即通过外化行为洞察内在的思维和能力。为此，本次以小学数学四年级综合实践活动探究“四边形内角和”为例，尝试实践表现性评价的案例。

一、活动任务设计

（一）适用教材内容：人教版小学数学四年级下册第五单元《三角形》

（二）时间：课后拓展、单元测评

（三）地点：教室

（四）活动准备：任意四边形若干个、剪刀

（五）任务设计：猜想四边形的内角和是多少度？

以小组为单位，证明猜想。详细写出你的想法。

（六）设计意图：

“图形与几何”是小学阶段数学课程的重要内容，也是开发学生思维的必要课程，对学生的核心素养的形成与发展具有直接的影响，“四边形内角和”是四年级下册，学生学习了三角形内角和的基础上一个拓展和延伸。设计“四边形内角和”作为表现性评价的任务，利于SOLO分类理论的对学生思维层次分析，主要是考虑到此知识对学生思维能力的考察比较有代表性，学生通过小组研讨四边形内角和，经历猜想、观察、思考、推理、归纳的过程，不同的学生呈现出不同的数学思维层次，表现出来的探究推理能力，体会转化的数学思想，形成解决问题的方法的能力都不同，能很好地实现过程评价的目的。

二、评价结果

（一）学生的总体表现

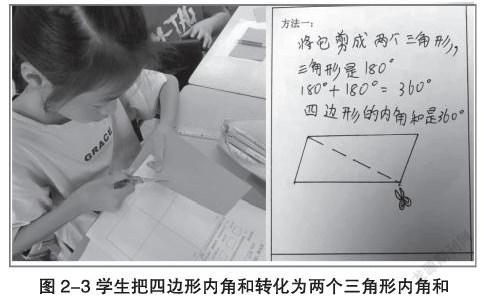
本次测试样本是四年级二班53人，通过表现性任务评价过程发现：在提出问题猜想时，约72%学生都能进行大胆而有依據的猜想，大多数学生猜测的依据的正方形、长方形也是四边形他们的内角和为四个直角也就是360°，所以猜测任意的四边形内角和也是360°;20%学生能提出猜想，但没有依据，凭感觉提出，认为对四边形内角和的猜想很陌生，不敢提出猜想;在验证猜想过程中，小组成员大多数能做到积极讨论，自信地表达观点，并能运用动手操作出实例来佐证自己的观点，大多数同学能听他人分享的观点，有序地参与讨论，但有小部分同学比较懒于动手，等待小组其他同伴的思考劳动成果，如下图为学生小组讨论环节。

从学生验证出的成果来看，超过一半的学生能想到两到三种方法去验证四边形内角和的方法。由于刚学三角形内角和，则极大多数学生能想到的是把四边形沿对角分成两个三角形，发现四边形的四个角之和就是两个三角形内角之和，四边形内角和=180°+180°=360°;

其二，也有很多同学们用最直接的方法，用量角器直接量出四边形四个角的度数，再把四个角加起来，考虑测量的误差，也能证明四边形的内角和为360°;

还有些学生想到了很童真的做法，直接把四边形的角挖出来，再重新拼起来，发现刚好围起来一个“圈”，即四个角组成了一个周角360°;

还有少部分同学觉得用正方形或长方形的内角和是360°的特殊情况直接认为四边形的内角和是360°，极少数同学能通过探究拓展总结多边形内角和的求和公式（n-2）×180°;极少数同学不会提出自己的想法。

（二）基于SOLO分类理论的学生思维层次分析

基于以上学生的表现情况，我们对学生探究“四边形内角和”的结果有了进一步的了解。但对学生数学学习的质性评价不仅仅关注结果，还需要关注认知过程，需要建立思维能力培养的层次。而SOLO分类理论，就是针对学生解决某一具体问题的表现，通过描述分析学习结果在思维结构上的复杂程度，反映学生从“量变”到“质变”的过程。依据SOLO分类五种思维水平的层次水平划分和描述，笔者对四年级学生解决此题的思维层次做了进一步的分析：

1.前结构水平（1人，约占比1.9%）：“四边形有四个角”这种回答，说明学生没有读懂问题的意思，思维混乱，凭自己感觉乱写一句话。

2.单结构水平（6人，约占比11.3%）：“我知道正方形的内角和是360°”或“我量得长方形的内角和是360°”“我量得平行四边形的四个角是360°”这类学生只考虑自己熟悉的个别四边形的或特殊的四边形，知道它们的内角和是360°，并没有从特殊推导到一般性，单凭一点论据就跳到答案上去，虽然这些同学有一定的思维能力，但这些同学的回答显示了浅表性的思维结构。

3.多点结构水平（40人，约占比75%）：“我用了如下方法知道四边形内角和是360°，方法一：用测量的方法量得一个四边形四个内角之和都是360°;方法二：我还会把一个四边内角撕出来，拼在一起刚好形成一个周角;方法三：我还能从把一个四边形的四个内角和分化为两个三角形的内角和180°+180°=360°去证明四边形内角和是360°。”

这些学生找到了多个解决问题的思路，分别去证明四边形的内角和，对问题有了更多的理解，有一定的思维能力，但是却没能把这些思路有机地整合起来，从回答的方式看，基本上只注意孤立的素材和方法，而使回答收敛太快，没形成相关问题的关系网络。

4.关联结构水平（5人，约占比9.4%）：这些学生也找到了如上“多点结构水平”的多个解决问题的思路，并且还会加以思考“我们小组通过合作实践，不管选出正方形、长方形、平行四边形还是一般的四边形，都能通过‘测量法’‘撕拼法’‘转化为两个三角形内角和’的方法，证明四边形的内角和为360°，综合可知，并不是特殊的四边形如正方边形、长方形的内角和才是360°，任意一个四边形内角和都是360°。”处于这一结构层次的学生对问题的要求有了一个整体的把握。他们能利用关联进行整合，有一定的归纳能力，基本能独立解决较为复杂的具体问题。

5.抽象扩展水平（1人，约占比1.9%）：这是最高的水平层次，更强的专研精神和创新意识，这类学生不仅能对四边形内角和问题有了整体的把握，还能够对问题本身进行有逻辑性的演绎和拓展，由四边形内角和的推导方法，拓展五边形内角和甚至n边形内角和也可以用转化为多个三角形内角和来推导出内角和为（n-2）×180°，导出新的更具有开放性和抽象性的假设或理论，从而能举一反三，将其运用于新的问题情境中。

（三）对教学的启示

1.表现性评价开阔教师的评价视角

综合以上分析，10岁左右学生正常应处于多点结构思维水平，对照基于SOLO分析数据，大部分学生均属于这一思维水平，还有11.3%学生超过了正常水平，达到关联和抽象扩展思维结构。由上案例，可观教师以评价对错为重心转移到学生回答问题的思维结构水平上，其评价标准不是预设的，而是游离和价值多元的，这些都可能引发新的思考，这些新的思考往往成为新思想、新发现的重要来源。这对指导教学评价学生的数学思维具有重要的现实意义，尤其在小学数学“图形与几何”板块个更能为一线教师的教学评价提供借鉴作用。

2.表现性评价促进师生的整体建构

表现性评价在评价学生的创新精神、实践能力、合作精神、学习兴趣、学习惯等方面具有相当明显的优势，从内涵上与新课程的评价理念息息相通。在小学生数学实践活动中引进它，将它作为现有小学生数学学习评价制度的一种补充，能切实地有效促进学生思维和实践能力的提升，这也指向深度学习提供了要素保障。同时也为教师发现学生存在的问题，及时调整日常教学提供了一个很好地沟通和改进机会，而这些也有力地促进师生共成长，整体建构意识也会进一步提升。