基于思维开发的初中数学课堂教学践行

孙静

摘要：“双减”背景下，对学校教育和课堂教学提出了更高要求，数学课堂在学生数学知识学习、数学核心素养培育和思维能力培养方面有着非常重要的作用。教师应当注重科学设置问题，激发学生学习和探究兴趣，搭建层次清晰的“脚手架”，让知识自然生成，让学生的思维自然生长，逐渐形成思维模式，以此方式完成教学目标。故本文将分析初中数学课堂中存在的问题，并以思维开发为核心，讨论实际教学策略。

关键词：思维开发;初中数学;思维模式

“双减”政策下，初中数学学习对学生思维能力提出了更高要求，要求学生应当具备较强的理解能力。在传统课堂教学当中，教师运用填鸭式教学传递知识，学生一味地接受，这种枯燥的教学方式难以提高其学习兴趣，也无法促使思维逻辑形成，使得教学质量和学习效率低下，学生思维固化。因此教师应在教学当中将“思始于问，问源于学”的理念融入课堂教学中，以问题的方式带动学生思考，提高学习兴趣，并逐步培养思维模式，最终完成教学目标。

1   “问”源于“学”，“问”为了“学”

“双减”政策的落地，对学校教育和课堂教学提出了更高要求，数学课堂在学生数学知识学习、数学核心素养培育和思维能力培养方面有着非常重要的作用。在目前的数学课堂教学中依旧存在一定问题，主要包括三方面。第一，提问作为教学的一种引导方式，教师在设立问题时缺乏具体的指导性。在实际教学过程中，一个好的问题能够发挥带动课堂节奏的作用，在提高学生教学参与度的同时，也保证了其学习状态。故明确具体地提出问题，可以加强教学质量。但是很多教师所提出的问题往往过于简单，暴露了过度注重课堂氛围的本意，难以对学生的思维和能力起到培养作用。第二，课堂提问的范围过于分散，问题所涉及的范围不集中。教师在提问时，除目的模糊外，问题所涉及的范围较为分散，没有根据教学内容与学生的发展规律进行设计，使得问题范围不集中，内容匮乏，对学生学习的积极性造成不利影响。第三，教师在运用提问进行教学时，要逐步引导学生进行思考，从而带动学习积极性，提高学习兴趣，这就要求提问的問题应当具备一定层次性，但是从实际情况分析，教师在提问时，其问题缺乏层次性，难以起到引导作用，也无法促使学生对问题进行思考，从而使教学质量大打折扣，降低学习效率。

2   “思始于问，问源于学”思维开发教学模式应用

2.1体现问题的指导性

在初中数学学习过程中，要求学生具备一定的逻辑性和理解能力，尤其是在逻辑思维的形成过程中，教师扮演了重要的引导角色，因此赋予问题引导性，可以逐步促使学生思维和逻辑性形成。结合实际教学目标与学生具体学情，精心设置问题，通过一系列追问，引导学生对问题进行探究和思考，在教学中培养学生的思维能力和学科素养。在数学课堂教学中，教师将引导性提问融入教学中，在提高学生学习兴趣的同时，还能引导其对课本中的知识进行学习和了解。提问作为教学当中广泛应用的一个方法，这种方法类似一个路标，给予学生学习的方向。想要利用好提问，就需要教师结合教学内容设计教学情境，逐步将其带入其中，在这个过程中完成对知识的学习。

案例1：在苏科版七年级上册“丰富的图形世界”当中，教师便可以说：“大家请对自己手边的文具进行观察，看看它们是什么形状的。”学生通过观察后得出答案。教师分别对学生进行提问，同时针对其得出的答案进行总结：“我们在观察物品的时候，应当学会简化去观察，通过简单的图案对物品几何特征进行抽象描述，包括圆柱体、圆锥体、正方体、长方体和球体。”以这种教学方式加深学生对图形的认知，从而学会观察方法。以这种引导性提问方式，促使学生对课本知识进行初步了解，带动其主动对问题进行思考，教师针对学生提出的问题进行解答，融入“思始于问”的理念，有利于教师后续教学内容的深入，在营造良好学习氛围的同时，引导学生进入状态，最终完成教学目标。

案例2：苏科版七上“正数与负数”教学片段

问题思考：根据天气预报，杭州市某日的最高温度为8℃，这天的温差是10℃，当日杭州市的最低温度是多少？你如何表示？

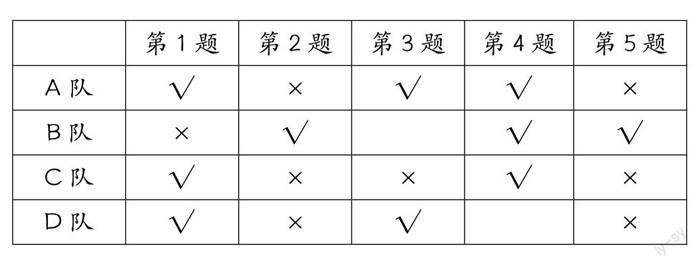
追问1：A、B、C、D四个代表队参加“学党史”知识竞赛，评分标准是：答对一题加5分，答错一题扣5分，弃权得0分;A、B、C、D四个代表队答题情况如下表：

根据已学过的知识，你能计算出A、B、C、D四个队的最终得分吗？

追问2：在解决问题的过程中，我们发现以前学过的数不够用了，你有办法解决吗？

追问3：“四川某地最低处的海拔高度为-263m”中“-263”表示什么含义？

追问4：上海户籍人口自然变动自1993年以来连续17年呈负增长态势，至2009年末，上海市常住人口自然增长率为0.27%，其中户籍人口自然增长率为-0.102%。-0.102%表示什么含义？

追问5：认真观察并思考，-2、-5、-263、-0.102%，它们有什么共同特征？对于数字0，你有什么认识？（总结负数特征，引入负数概念）

以现实生活为素材，创设一系列问题情境，设置层次递进的问题串，让学生感受到数学源于生活，力求通过数学与生活的联系，帮助学生更好地感受数学的本质。在感受到已学过的数不够用之后，发现引入一种“新”数的必要性，在此基础上正确认识并理解正数、负数和0的意义，尤其是对数字0的重新认识。通过问题情境教学，在学生逐步将知识概念的生成过程中，有利于学生思维品质的培养。

2.2发挥问题的激疑性

在整个学习过程当中，学生都是充满好奇的，在应用引导性问题之后，教师可以充分利用学生对新知的渴望和思维发展的自我要求，以问题串的形式搭建层次清晰的“脚手架”，让知识自然生成，让学生思维自然生长，逐渐形成思维模式，从而提升课堂教学有效性，以此方式完成教学目标。所以，教师在数学课堂教学中可以根据学生已经了解的知识，选择一些疑问性问题来激发学生思考。在这个环节中教师充分发挥主导作用，注意问题不应当立即给出答案，而是要经过学生不断分析和研究得出。

案例3：苏科版七年级上册“图形的运动”中，教师可以让学生选择手边任何一样物品，将其中一点固定，旋转一周，并将其运动的轨迹图像画出来，然后以小组形式到前面展示。有些学生可能会利用手中的笔，也有的学生会使用课本，因此最后得出的答案也不相同，尤其是一些学生利用较为复杂的物品时，他们对得出的图案形状表现出了较强的好奇心。最后在展示环节，教师调动学生积极思考，分别对图形进行讨论和评估，获得共同认知：在绘画运动轨迹的时候，要将固定的位置看成一个点，将移动的另一端看做另一个点，两点之间为一条线，这条线运动的轨迹为面，那么旋转或移动一周的面，就是我们最后得出的图形，老师再进行总结。这种方式不仅体现了图形运动的轨迹，也教会学生自主观察物品的移动。教师也可以选择一样物品为学生示范，将物品有规律地移动，让大家说说看到的图形运动轨迹是什么样的。有的学生可能看到的是扇面，也有的学生看到的是平行四边形。此時教师可以利用问题来激发学生的好奇心：“移动的轨迹是一样的，但是为什么大家最后得出的结果是不一样的呢？”再选择几名学生进行提问，重点询问他们的观察点是什么，最后得出结论：“大家看我手中的物品有四个边，当我固定在这一点的时候，一些同学是以右上角的边为观察点，然而有的同学是以左上角的边为观察点，这也是为什么大家最后得出结论不同的原因，我们从中可以学到，运动的轨迹图形是以你的观察点所形成的，所以这四个边的运动轨迹，最终就会形成四个图案。”这种留有伏笔的教学方式可以激发学生好奇心，并且增强了其教学参与感。

2.3体现提问的层次性

以上方法均遵循了思始于问的原则，主动激发学生的学习积极性，引导他们对问题进行思考，从而提出问题，教师再针对问题进行解答，均是围绕着教学目标进行的。然而如何进行提问来体现问题的层次性？则是将重点放在了“问源于学”中的“学”上。在实际教学过程中，教师通过层次性问题逐步引导学生思考，并将重点放在“学”上，不断理解数学知识，最终完成教学目标。

案例4：苏科版七年级上册“垂直”的学习当中，教师可以先在黑板上画出垂直的两条线，并提出问题：“大家是否在生活中观察到这种角度？”以此问题引导学生去主动观察和思考，有些学生可能会观察到教室屋顶的四个角是垂直角度，也有学生会观察到教室的门与地面是垂直角度。教师继续提出问题：“大家观察的没错，那么大家知道一个圆是多少度吗？”有些学生可能对此有些了解，也有学生对此表示疑问。教师给出答案：“有些同学应该知道，一个圆，也就是我们转一个圈，这个角度是360°，那么这两条线是多少角度呢？”通过对学生的提问和引导最后得出答案：“如果将这两条线延长，我们将会得到一个十字，那么这个十字的角度就是360°，其中的一个就是90°，我们称这种90°的角为垂直。”以这种层次性问题引导学生思考，并在下一环节设立一个新问题，加深学生对垂直角度的印象。这种教学方式促使学生去主动观察和学习，强调了“问源于学”。

案例5：在进行二次函数图像和性质的应用复习教学时，可以进行这样的教学设计：

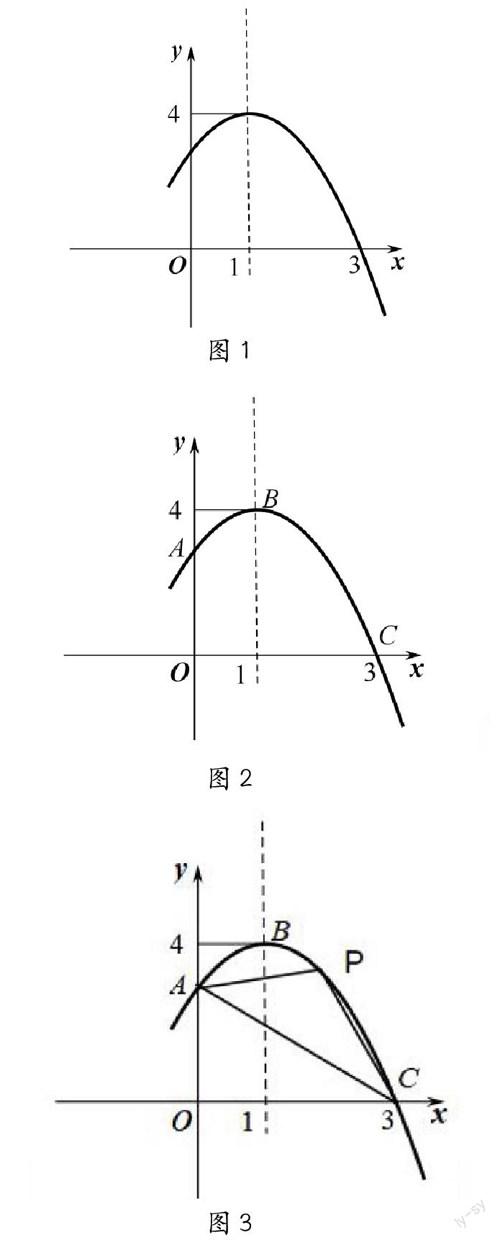
问题思考：观察如图1所示的二次函数图像，结合图像你能获得哪些信息？先独立思考，后与同伴交流。

追问1：如何求这个函数的表达式？

追问2：如何平移二次函数图像使得它经过原点？求此时二次函数的表达式？（多种方案）

追问3：从图像中能挖掘到方程的信息吗？借助图像我们可以得到一元二次方程的解吗？

追问4：还能挖掘出图像与不等式的关系吗？

追问5：在图中你能看到线段吗？你能求出它们的长度吗？

追问6：如图2，图像中有四边形吗？你能求出四边形ABCO的面积吗？

追问7：如图3，若在第一象限图像上存在一动点P，请你提出一个与二次函数相关的问题，并尝试解决问题。

通过这样的教学设计，引导学生从数学知识的本质特征和内在联系理解二次函数，从函数图像上点位置的“直观变化”和函数表达式确定的“数量变化”内在联系来掌握二次函数相关知识，即一种思想：数形结合思想;两个基本性质：轴对称性，增减性;三种表示方法：一般式、顶点式、交点式;四个注意点：a的意义，二次函数的函数值大小，抛物线的平移变换和轴对称变换，方程、不等式问题与二次函数的关系。通过层层递进的问题思考，引导学生从“发现”知识的过程及联系中培养思维能力。

3   结语

总体来说，在初中数学的教学当中，关键就在于“思始于问，问源于学”中，通过这种方式来引导学生主动思考，并提出针对性问题，教师进行解答，并引出下一个问题，将其带入学习状态当中，利用引导性、激疑性和层次性问题来促使学生思维形成，培养思维能力。

参考文献：

[1]董军.小组合作学习模式在初中数学教学中的应用[J].学周刊，2021（34）：105-106.

[2]王希军.谈初中数学自主探究式教学[J].学周刊，2021（34）：107-108.

[3]叶莉.中学数学教学中学生思维能力培养路径分析[J].学周刊，2021（34）：109-110.