咬文嚼字，提升学生思维品质

丁元清

[摘 要]小学数学教学同样要重视咬文嚼字。教学时，在知识建构时，让学生初次学习时就对概念、性质、规律等中的每一个字词咬文嚼字，提升学生思维的深刻性;在解决问题时，让学生对题目中的关键字词咬文嚼字，从而厘清条件与问题，明确条件与问题的内在联系，为学生正确解决问题打好基础，提升学生思维的严谨性;在辨析易错题时咬文嚼字，关注和研究学生在解答哪些题目时容易出错，深入探析易错原因，提升学生思维的思辨性;在备课时咬文嚼字，注重教师自身教学用语的规范性、科学性、严谨性，让学生感悟在数学学习中将语言文字表述准确、理解到位的重要性，提升其思维的广阔性。

[关键词]概念;易错题;咬文嚼字;思维品质

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2022）14-0043-03

语言文字是交流思想和情感的工具，是思维的载体。数学教师在平时的教学中要重视咬文嚼字，这样可以促进学生理解和掌握数学知识，建构完善的知识体系，提升学生数学思维的严密性、精确性。下面，笔者通过教学案例实践，谈谈在小学数学教学中咬文嚼字的策略。

一、在知识建构时咬文嚼字，提升学生思维的深刻性

数学中有很多的概念、性质、规律，其内涵丰富，用词精当，多一字不行，少一字不可，教学时需要教师及时引导学生对其中的关键字词进行分析，让学生知道其内涵要义，了解其外延范围，抓住其含义本质，以学生的知识建构为支点，让学生初次学习时就能对其中的关键字词咬文嚼字，透过现象理解本质，提升学生思维的深刻性。

例如在教学“商不变规律”时，上课伊始，教师先给学生讲“猴子分桃”故事：4个桃子分给2只猴子，每只猴子分得几个？40个桃子分给20只猴子，每只猴子分得几个？400个桃子分给200只猴子，每只猴子分得几个？4000个桃子分给2000只猴子，每只猴子分得几个？然后提问：“在这个故事中，什么变了，什么没有变？”让学生通过浅显的故事初步知道桃子总数、分桃子的猴子数在变，但每只猴子分得的桃子数都是2个，不变。这是在认知起点向学生渗透咬文嚼字的重要作用，使其抓住要点，知晓“变”与“不变”的概念内涵。接着，教师让学生研究4÷2=2，8÷4=2，16÷8=2，28÷14=2这些算式中什么变了什么没变，再让学生探究其中被除数、除数是怎样变化的（从前往后看）。这时学生模糊地意识到“被除数和除数同时乘一个数，商不变”。教师问“真的是这样吗”，并举例子4÷2=2，（4×2）÷（2×2）=2，（4×8）÷（2×8）=？，引导学生咬文嚼字，让学生弄清楚被除数和除数同时乘的数应该是什么样的（凸显“相同的数”）。为学生构建商不变规律中“被除数和除数同时乘一个相同的数，商不变”的概念时，强调“两同”，即“同时”“相同”;再让学生从后往前看，看看有什么发现，弄清楚“被除数和除数同时乘或除以一个相同的数，商不变”。其实这时对规律的讲解还欠一点火候，可以进一步提问“这里的数可以是任何数吗”，以激发学生的思维，将学生引向深度思考，让学生知道为什么还要将“0除外”。最后则水到渠成地为学生构建完善的“商不变规律”的概念。在这个过程中，教师通过引导学生咬文嚼字，让学生厘清思路，使学生的认知从模糊走向清晰，数学思维得以提升。

数学是一门基础性学科，很多概念、规律等的构建过程有着广阔性、逻辑性、深刻性，这不仅仅反映在学生的学习成绩上，更重要的是能折射出一个人的思维品质的优劣，会影响学生的学习和生活，伴随其终生。数学课堂教学中的咬文嚼字要规范、科学，尽可能减少日常用语对严谨的数学思维的干扰，还要注意对如近义词、多义词等的词义进行辨析，更要注意对算术、代数、几何中的常用词，以及修饰关系语句进行深入分析。

二、在解决问题时咬文嚼字，提升学生思维的严谨性

学生在学习知识后要能应用所学知识解决问题，而解决问题的过程是学生与学习内容、教材、题目等进行对话、产生交互作用的一种方式。在解决问题时咬文嚼字，是指对题目中的关键字词进行分析，以深刻理解题意，找出条件与问题，厘清条件与问题的內在联系，使要解决的问题在学生头脑中形成一个清晰的印象，为解决问题打好基础。教师可以让学生边读题边思考每句话的含义，理解每一个符号的意思、不同条件之间的关系，一方面促进学生对知识的理解，另一方面培养学生边读题边思考的良好习惯，让学生通过解决问题，提升思维的严谨性。

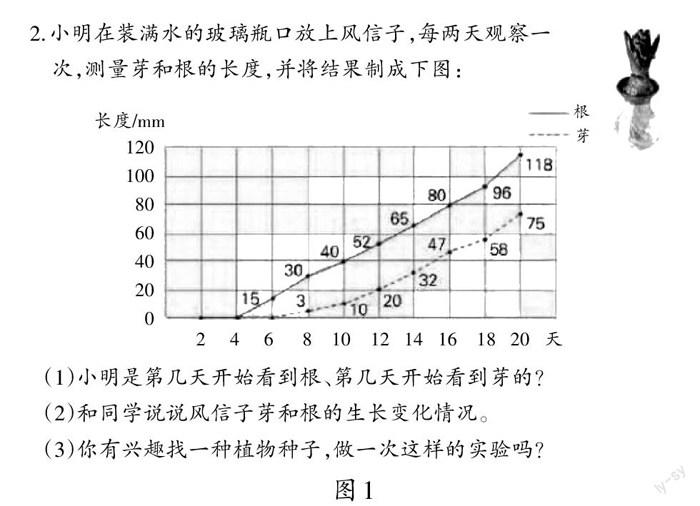
【例1】苏教版五年级下册第25页练习题（如图1）教学情况

在笔者请学生阐述自己的理解时，两位学生出现了不同的看法。学生甲认为根第4天的长度为0 mm，第6天的长度为15 mm;芽第6天的长度为0 mm，第8天的长度为3 mm，所以小明是第6天看到根，第8天看到芽。学生乙认为虽然根第4天的长度为0 mm，第6天的长度为15 mm;芽第6天的长度为0 mm，第8天的长度为3 mm，但根不是第6天一下子长到15 mm的，线段图起始点在第4天，因此小明是第4天开始看到根。同样的道理，小明应该是第6天开始看到芽。其他学生随着他们两人的争论形成了两种不同的意见，一时无法统一。

是直接说出答案，还是让他们继续找理由说服对方呢？笔者灵机一动，想到不妨让他们咬文嚼字，感悟一下，于是笔者提问：“请同学们想一想，题目问的是什么？该怎么理解‘看到？或者对于问题‘小明是第几天开始看到根、第几天开始看到芽的？，你认为答案是什么？”有学生说，看到根，有可能根才长出一点点，量不出长度，看到芽，有可能是才发芽，同样量不出长度。

在学生进一步明确这些细节之后，笔者追发问：“看到根和看到根的长度是一回事吗？看到芽和看到芽的长度是一回事吗？”学生异口同声地说不是一回事。

通过这样的对比让学生主动咬文嚼字，理解“上升”是一种趋势，明白其从何时开始到何时结束，培养了学生思维的严谨性、深刻性。在解决问题的过程中咬文嚼字，不只是简单的动嘴的过程，更是一个动脑的过程、思考的过程，是一个加深理解提升思维品质的过程，是一个不断完善建构知识体系的过程。学生在学习的基础上进一步解读消化这些信息，进而完成知识的获取，实现知识体系的建构。

三、在厘清易错题时咬文嚼字，提升学生思维的思辨性

学生在解决一些问题时容易出错，往往是因为没有对题目好好地咬文嚼字，把一些关键字、词、句弄混，造成低级错误。在厘清易错题时咬文嚼字，也就是要关注、研究是什么原因导致学生在解答时出错，要弄清楚错因，以此为支点，提升学生思维的思辨性。例如：

1.走楼梯问题

【例2】小冬和小亮同住在一幢大楼里，小冬住5楼，小亮住4楼，小冬每天回家要走80级台阶，小亮回家要走多少级台阶？

学生解答时很容易犯的错误是“80÷5=16（级），16×4=64（级）”。仔细分析这个错误，表面的原因是学生把实际走4层楼的台阶当成走5层楼的台阶去计算，深层次的原因则是学生对生活中的数学常识缺乏了解。如果有了对生活实际的了解，在读题目时对“小冬每天回家要走80级台阶”进行咬文嚼字，思考清楚第几层和几级台阶的意思，明白80级台阶是走了几层、每层有多少级台阶，解答时思路就不会出现错误了。思路清晰了，学生自然就不会做错题目了。

生活中，走楼梯问题就如同植树问题，楼层数相当于树的棵数，而走的台阶层数就相当于间隔数，解答时要多联系生活实际，或者画图辅助解答，才能少犯错误。让生活走进课堂、课堂呈现生活，学生的思维就会被有效激发。

2.行程平均速度问题

【例3】李明上午上学时从家里去学校每分钟走60米，中午回来每分钟走40米。求：他从家到学校来回平均每分钟走多少米？

实际教学中，很多学生会做出错误解答“60+40=100（米），100÷2=50（米）”。求来回的平均速度，應该用来回路程的总和除以来回用去的时间总和。学生解答错误显然是因为没有对“来回平均每分钟走多少米”进行咬文嚼字，想当然地把来回当成两次，把速度当成路程，直接用速度之和除以2。如果对“来回平均每分钟走多少米”进行咬文嚼字，抓住求平均速度的数量关系进行思考，就不会出现这样的错误了。

3.分数中数率相混问题

【例4】有两根10米长的绳子，第一根先剪去1/5，第二根先剪去1/5米，哪根剩下的部分长？

对于这道题，学生容易犯的低级错误是：第一根剩下的部分长10- 1/5=9.8（米），第二根剩下的部分长10- 1/5=9.8（米）。究其原因，是因为原来两根绳子都长10米，第一根剪去的是10米的1/5，剪去2米，剩下8米;第二根剪去的是1/5米，即0.2米，剩下9.8米，学生没有对“剪去1/5”和“剪去1/5米”进行咬文嚼字，分析出“剪去1/5”表示剪去的长度与原来长度的关系，而“剪去1/5米”表示剪去的就是0.2米，没有思考比较1/5后面带单位和不带单位的不同。

实际教学中，像这样的问题还有很多，如三年级时锯木料的段数和次数，四、五年级乘车问题中起步价和起步价外的收费标准，五、六年级有关用水、用电的分段计费等，在此仅举这三个例子加以粗浅说明，其中需要咬文嚼字的情况大同小异，就不再一一赘述。

四、在备课时咬文嚼字，提升学生思维的广阔性

一些数学教师教学的班级学生总体成绩一般，教学效果总是处于中等水平，学生中优秀者偏少，深究其因，就是教师在教学中随意性比较大，没有做到咬文嚼字，最终是“以其昏昏使人昭昭”。课堂教学实践告诉我们，数学教师备课时要重视对教材相关文字的研究，深入理解教材编排的意图，通过咬文嚼字汲取编者的经验，从学生的实际出发进行教学，用好课本，认真研究课本上的每一个概念、性质、计算公式等。在备课时咬文嚼字，就是教师要认真研究教材，更要在教学时引导学生对概念、性质、计算公式、题目等认真地读、慢慢地品、细细地嚼。无论是课堂教学还是平时练习，抑或与学生的交流过程都要咬文嚼字。

例如，对于“有红、黄、蓝10个除颜色外，外形都一样的球，从中任意摸一个球，要使摸到红球的可能性最大，摸到黄球的可能性次之，摸到蓝球的可能性最小，红、黄、蓝球各有几个？”这道题，正常情况下学生会有两种答案：其一（正确），7个红球，2个黄球，1个蓝球;其二（错误），9个红球，1个蓝球。如果仅从答案是正确还是错误的角度来考虑就很简单，但是教师要善于引导学生咬文嚼字，引导学生思考第一种答案对在何处、第二种答案错在何处，正确答案是不是只有这一种情况，再总结：从“有红、黄、蓝10个除颜色外，外形都一样的球”可知，每种球至少有1个。结合“摸到红球的可能性最大，摸到黄球的可能性次之，摸到蓝球的可能性最小”可以确定，第二种答案是错的;第一种答案只是正确答案中的一种，其实只要满足“红球个数+黄球个数+蓝球个数=10”，红球个数最多，蓝球个数最少，黄球个数介于两者之间即可。这样引导，让学生不是简单地只顾题目做得对或错，而是对每一道题都认真地咬文嚼字，使其思维从浅层次走向深层次，从习惯性思维走向发散性思维，从被动做题走向主动研究题目，从而实现思维品质的真正提升。

数学思维能力是学生核心素养之一，在小学数学教学中渗透咬文嚼字的观念，可以逐步培养学生数学思维的深刻性、严谨性、思辨性。教师紧扣提升学生数学思维品质这一主旨，把握住以上教学案例所述的方法，对数学概念、性质中的核心词汇，以及题目中的词、短语和句子等进行咬文嚼字，做好字斟句酌的示范，做到严谨治学，尽量避免含糊和混淆，并培养学生思维的严谨性。持之以恒，学生的思维品质必定会得到有效提升。

（责编 吴美玲）