优化估算题组教学的实践研究
2022-05-30施小锋
施小锋
[摘 要]题组教学是根据学生的认知规律和思维能力,选用科学、合理、有效的一组具有渐进性的数学问题来组织课堂教学,实现有效教学的一种教学模式。基于SOLO分类理论,将学生数学学习的思维层次分为五个结构层次(水平)。在估算教学中通过借“题”夯“基”、顺“势”温“度”、巧“变”显“型”等教学策略,促进学生深度学习,提升学生的高阶思维。
[关键词]SOLO分类理论;估算;题组教学;高阶思维
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)14-0015-03
高阶思维是一种以高层次认知水平为主的综合性能力,如批判性地评价信息的能力、解决问题的能力、创造性思维能力等。纵观现行的估算教学,以下三“化”现象比较常见。
习题“零散化”:习题往往分散、孤立地出现,学生缺少综合比较、系统思考的历练。
功能“偏差化”: “怎么估”“看成多少”“结果是多少”等低效问答频频出现,虽然注重算法的习得,却弱化了思维的发展。
思维“浅表化”:缺乏能激发学生高效、深度参与的活动和载体,学生只会觉得“要我估算我才估算”,思维浅化、窄化。
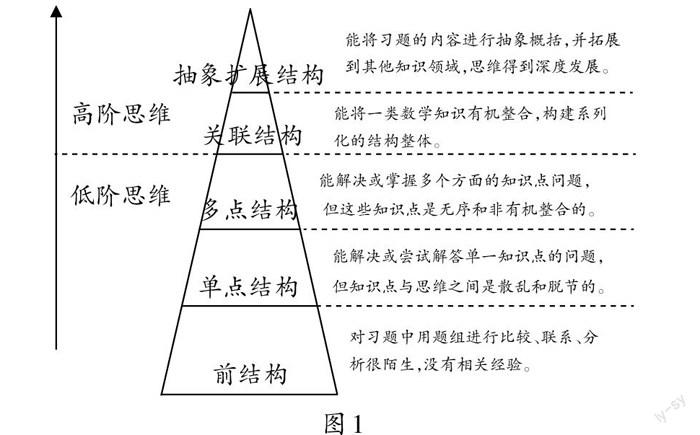
根据可视的学习结果,可以将学生数学学习的思维层次依据SOLO分类理论进行划分(如图1)。
估算对于提升学生的运算、推理、思维、表达等数学能力有着非常重要的意义。如何追本溯源,从源头上消除三“化”现象,破解估算教学的难点?实践表明,通过题组教学,能治标,更能治本。
本文以乘除法中的估算教学为例,借助题组教学,系统性地借“题”夯“基”、顺“势”温“度”、巧“变”显“型”,引导学生感知、理解与建构数学模型,促进高阶思维的发生。
一、借“题”夯“基”,思维由“单点结构”走向“多点结构”
“單点结构”层次,是指能找到一个解决问题的方法或思路,然后凭这个方法或思路进行点对点的对接,以解决问题。“多点结构”是指能找到多种解决方法,但是这几种方法之间是孤立的,而非整体和整合的。
根据题型的特点、题目的价值和功能构成的估算题组,可以让学生感受到估算方法的多样性,有效促进学生的思维从单点的一维走向多点的多维。
【例1】估算比大小:①252.4÷6.38和56×0.76;②4÷7和11÷23。
师:利用合适的估算方法比较每组中两个算式的大小。说说是怎么估算的,为什么这么估算。
生1:题①252.4÷6.38可以估算成240÷6=40。估算56×0.76时,可以把56看成60,把0.76看成 0.8,得到48,比40大。故252.4÷6.38<56×0.76。
生2:把56和0.76都估大了,结果大太多了。可以把0.76看成[3/4],56×0.76≈56×[3/4]=42,再与第一个算式比大小比较好。
师:很好!两个数都估大,结果大太多了,这样说服力不强。
生3:题②的4比7的一半大,而11不到23的一半,故4÷7>11÷23。
教师提炼多种算法。(1)就近取整估算。就近取整估算是教材中最“浓墨重彩”的,也是运用最广泛、最有效的一种策略。整数是取整十、整百、整千数,小数是取整数或比原小数位数少一位或少几位的近似小数。(2)分小数互化估算。在小数乘除法计算时,把小数转化成接近的分数进行计算,会得到意想不到的简便效果。(3)引入中间量估算。引入中间量往往用于结果的大小比较中。(4)简洁性口诀估算。在乘法和除法中运用较为常见,就是在充分考虑数据特点情况下,直接利用乘法口诀估算结果。
教师将不同解法的习题“打包”整合成题组时,既要考虑到数据的一般性,也要考虑数据的特殊性,在数据的“取舍”与“进退”中培养学生思维的灵活性。
二、顺“势”温“度”,思维由“多点结构”迈向“关联结构”
“关联结构”的形成,需要学生将同类型的数学知识有机整合,构建系列化、系统化的结构体。顺着学生不同的思路,教师通过引导学生对解题方法的对比、联系和优化,打破方法间的壁垒,让学的思维从“多点结构”迈向“关联结构”。
1.对比方法,挖掘算法拓宽度
在不同的习题中,即使是相同的数据也有不同的处理方式。利用题组可对比不同的处理方法,能增强学生思维的主动性和敏锐性,更好地拓宽学生的估算视野。
【例2】估算:(1)232÷5;(2)232÷8;(3)232÷7;(4)232÷11。
师:都是232除以一个自然数,怎么估算?
生1:232÷5≈250÷5;232÷8≈240÷8;232÷7≈210÷7;232÷11≈220÷11。
师:同样是数据232,为什么估成的数却不一样?除数是多少时,才把232看成230?
生2:除数是23或者是10的时候。
估算应“先估后算”。估算的两个重要因素是“方便计算”和“尽量接近”。通过题组对比,学生明白估算的方法是多元的、开放的,所要估的数不是一成不变的,需要根据参与运算的其他数的变化而变化。只有“高瞻远瞩”,深谙数据变化将引起估算方法改变之道理,增强方法间的融通与变化,才能拓展思维的宽度和广度,“关联”更多可能。
2.联系方法,基于情境增厚度
相同的算式,在不同情境中的处理方法和结果会大相径庭,而不同的情境又隐藏着相通的策略,此时可借助现实的数据情境进行教学。
【例3】(1)胜利小学有28个班,平均每班32人,共有980个座位的电影院能全部坐得下吗?(2)加工车间要进货28箱零件,每箱重32千克。一辆核定载重800千克的小车一次运完这些零件会超载吗?
生1:题(1)用估大法。28×32≈30×32=960,比980小,因此坐得下。
生2:题(2)可以采用估小法。28×32≈28×30=840,比800大,所以超载了。
师:相同的算式28×32,处理方法为什么不一样?如果都用估大或估小法可以吗?
生3:如果被估部分估小了,结果还大,那就一定大;如果被估部分估大了,结果还小,那就一定小。
情境是数学知识和儿童思维之间的桥梁和纽带。题组中的不同情境,可以让抽象与具象呼应,不断增强学生估算的变通性,增加学生思维的厚度,“关联”则更持久。
3.优化方法,突现本质显深度
解决一个问题,可以有多种策略,但一般都有一个相对简洁、简便的方法,在探寻与优化这个方法的过程中,需要学生具有批判性思维和创造性思维。
【例4】体育组要买一批跳绳,每根2.65元,五年级有172人,每人一根。(1)购物前思考“准备600元钱够不够”。(2)购物满400元可送护腕,这次购物能否获得赠送的护腕?(3)付款时思考“大约需要多少元钱”。(4)付款给收银员时,一共需要付多少元钱?
师:这几个小问题有什么区别和联系?分别用什么方法解决?
生:前面三个问题不需要用精算,选用估算即可,分别选用“估大法”“估小法”“四舍五入法”取近似数。最后一个问题则必须用精算。
只有对解题策略和方法了然于胸,将精算与估算方法前后贯通,才能根据数据的特点并结合问题要求,适时选择精算或估算,或合理、正确选择估算的方法。在方法优与劣的对比中,在合适与不合适的甄别中,学生的思维向纵深处发展,“关联”更自然、更坚固。
三、巧“变”显“型”,思维由“关联结构”跃至“抽象扩展结构”
“抽象扩展结构”是指学生能够对问题进行抽象地概括,从理论的高度来分析问题,使问题本身的意义得到拓展和延伸。教师要在“关联”的基础上,引导学生继续深入感受方法,并借助一定的符号,用简单的方式进行表达,使学生在理解、运用和创造过程中更高效地理解估算的意义。
1.变封闭练习为开放建构
模型是一种高度抽象和概括的表达形式。開放题题组,可让学生在对多个数据的假设和还原中感受方法的普适性和策略的统一性。
【例5】(1)2名教师带着35名二年级学生去动物园参观。成人票5.8元/张,儿童票2.8元/张,只带120元钱够不够?
(2)将题(1)的数据进行调整:教师2名,票价5.□元,学生35名,票价2.□元,带120元钱是否够?
师:改编后,数据不确定,你还会做吗?
生1:可以设一些数。先设几个教师票的单价和学生票的单价,再估算,发现都比120元小。因此带120元钱够了。
生2:你这个方法比较麻烦!我是直接估算的,把教师票5.□看成6元,学生票2.□看成3元,总价不到120元。
师:这样估算可以吗?(有的学生认为可以;有的学生认为5.□可能更接近5元,学生票2.□可能更接近2元,因此不可以)
解决比较复杂的、条件不确定的估算问题时,可以引导学生通过“拎”(模型)、“定”(范围)、“比”(大小)、“答”(问题)四步解答。
拎:5.□×2+2.□×35( )120。
定: 5×2+2×35=80<5.□×2+2.□×35<6×2+3×35=117。
比:117<120。
答:117元是最多且不可能的情况,所以120元够了。
因为改编后的习题数据不完整,使得精算“断路”,所以在假设数据、分析数据的过程中,在提炼模型、深挖本质的过程中,学生的思维向高度抽象、深度建模发展。
2.变思维隐射为结果可视
从思维的角度,把抽象的表达转向直观的图形,并借助直观图形来理解抽象的内容。在将思维“锚点”可视、外显的过程中,学生能够有抓手且直观地学。
【例6】(改编例3):胜利小学有28个班,平均每班32人,“恒达影城” 共有900个座位,能全部坐得下吗?
生1:32×28≈32×30=960(估大法),比900大,坐不下。
生2:32×28≈30×28=840(估小法),比900小,坐得下。
生3:我是这样想的,把32和28分别估成30,30×30=900。一个多估2,一个少估2,刚好抵消,能坐下。
生4:我喜欢生3的方法,但结果不应该刚好等于900。积的末位2乘8应该是6。
生5:我是实算(精算)的,32×28=896<900,坐得下。
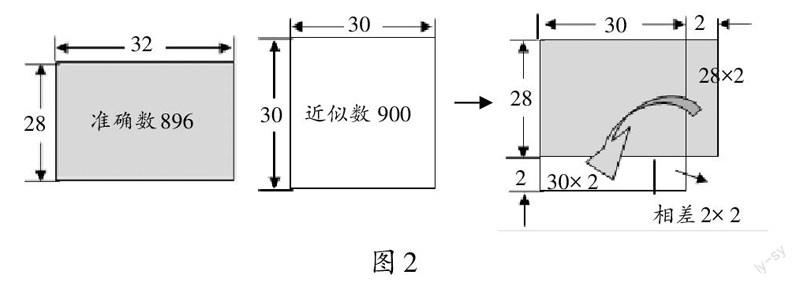
师:生3说的一个多估2,一个少估2,刚好抵消,而生5精算出来是896,为什么不正好是900呢?
师(出示图2):相差的4在哪里?
先反思不同的解题思路得出的结果,再比较误差。在“情理之中”却又“意料之外”的辨析中,学生能够借助直观图形进行解释,思维逐渐深刻。
3.变顺向思维为逆向思维
从模型出发,通过字母表达、文字说明、概括提炼等方法引领学生,能够促进学生逆向思维能力的提升。
【例7】括号中可以填哪些自然数?(1)502×( )≈3000;(2)6391÷( )≈8。
生1:题(1)可把502看成500,利用等式性质求出结果是6。
生2:题(2)可把6391看成6400,商是8,不难推导出除数是800。
师:题(2)只能是800吗?
生3:四舍五入后等于800的整数都可以,比如793、798、804等。
生4:题(2)可以转化成“( )×8≈6391”。把6391看成6400,看大了9,所以括号中最接近的整数是799。
生5:a×8≈6391,a就等于(6400-9)÷8=6400÷8-9÷8=800-1.125≈800。
要解答逆向思维的题组,就需要学生在运用模型解题的过程中对结果不断进行调整和修正,思维的缜密性大大提高。
基于SOLO分类理论下的题组教学,是对估算教学中单一习题教学的超越,是对数学学科整体性、结构性和学生学习规律的顺应。练习的负担轻了、思维的含量多了——学生在题组计算中能够联系方法、比较异同、优化策略;机械化的操练减了、综合化的运用增了——学生处理信息的能力更加“综合”和“通盘”;碎片化的调取少了、模式化的通透多了——在解题组的过程中,在模式的提炼和运用过程中,学生的思维拾级而上。“题海”无涯苦作舟,题组则是茫茫“题海”中的思维之舟。
(责编 金 铃)
