用十进位值制计数法贯通“数与运算”教学
2022-05-30万泉
万泉

十进位值制计数原理是学生建立数概念的基础和核心,也是学生理解算理、算法的依据。在小学阶段,促进学生感受十进位值制计数法的价值,理解并运用十进位值制计数系统学习“数与运算”,可以从以下几个方面着手。
一、构建计数单位模型,理解十进制
1.让计数单位有“形”
“十进制”和“位值制”是构成十进位值制计数系统的重要概念。数数和计数是人类生活和生产的需要,古人在探寻计数方法的过程中逐步形成了“满十进一”的约定,并由此从“一”开始,不断创造了一系列计数单位。若干个“一”“十”“百”“千”“万”等构成了数,也就是说,数的构成运用了十进制原则。学生对多位数的感受,应达到能在脑海中直观地反映出相应的计数单位模型及其个数的水平。在数概念的教学中,教师应充分重视计数单位模型的建立。
小棒、方块、点子图都是重要的认数工具,也是直观的计数单位模型。人教版数学一年级下册《100以内数的认识》用一根小棒、一小捆小棒、一大捆小棒,分别表示计数单位“一”“十”“百”;二年级下册《1000以内数的认识》用由小方块构成的“一条”“一片”“一大个”正方体,分别表示“十”“百”“千”。随着要认识的数逐渐增大,教材要求学生理解数的意义的方式也越来越抽象。建立上述计数单位模型的表象,有助于学生建立起抽象的数与现实中的数量之间的关联,感悟多位数的构成和大小。
教学时,教师通常会出示一堆散落的小棒或小方块,让学生用从小到大的计数单位完成数数过程,并追问“十”(或“百”)在哪里。以方块材料为例,学生可能这样表述:10个小正方体合在一起的“一条”就是“十”;10个“一条”合在一起的“一片”就是“百”。教师应及时用多媒体呈现10个计数单位模型合在一起的动态过程(如下图)。
当有更多方块出现时,学生会自然地想到用“百”这个大一些的计数单位去数,进而发现:10个“百”是一千,“千”是一个更大的计数单位。
用直观的方式将认数工具结构化,能帮助学生构建起计数单位模型的表象,感悟计数单位的大小及其十进关系。
2.用计数单位模型数数
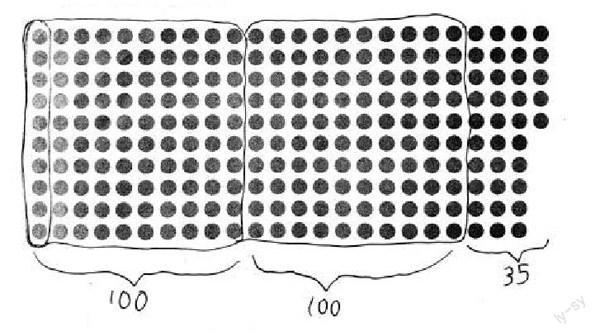
借助计数单位模型数数,是对十进制的巩固和运用。教材设计了数圆点数量的例题(如下图)。这样的数数问题需要学生主动运用十进制将点子图结构化,即将一列(10个)圆点看成一个“十”,将10列圆点看成一个“百”,从而自主构建计数单位的圆点模型,并利用该模型进行数数、计数。
学生数出圆点的数量(235个)后,教师有必要让学生用小棒或方塊模型表示“235”,让学生在多种认数工具的转换中融通同一计数单位的不同表征模型,使他们更清晰、直观地认识到数是由若干个计数单位构成的。构建和运用计数单位模型,能促进学生数数、计数能力的形成,培养学生的数感。
二、借助结构化计数器,理解位值制
1.用计数器数数
计数器是比小棒和小方块更抽象的数数工具。一根、一小捆、一大捆的小棒或一个、“一条”、“一片”、“一大个”正方体的外观不同,比较容易与不同的计数单位对应起来,而计数器上所有珠子的外观都相同,学生需要依靠珠子所在的位置去辨识不同的计数单位。同样一颗珠子,放在不同的数位上,就能实现以一当十、以一当百的效果。这体现了对小棒和小方块等计数工具的简化。例如,学生在个位上拨9颗珠子表示9个一,再拨1颗就有10颗珠子,10个一是1个十,个位上这10颗珠子就可以换成十位上的1颗珠子。以此类推,学生借助计数器就可以认识更大的计数单位。学生在计数器上熟练地拨珠数数,能深化对十进制计数规则(满十进一)的理解,强化对计数单位位置和顺序的感受。
2.用计数器记数,学习数的读写
数的记录运用了位值制原则,即先把各级计数单位进行有序排列,再把相应的计数单位个数用0~9这10个符号表示出来。这样就完成了一个多位数的抽象和记录过程。数的认识需要经历符号抽象的表示过程。
以“235”为例,运用计数单位模型表示数的组成,学生能直观地看到这个多位数由2个百、3个十、5个一组成;但在计数器上表示“235”,学生看到的是半符号化的2、3、5。从直观模型到相对抽象的计数器,再到符号“235”,这个从计数到记数的过程就是学生体会位值制的过程。
用计数器记录多位数时,要注意动作表征与语言表征的紧密结合。例如,在计数器上拨“235”时,学生应该这样表述:在百位上拨两颗珠子表示2个百,在十位上拨3颗珠子表示3个十,在个位上拨5颗珠子表示5个一,合起来就表示“二百三十五”。边操作边表述,不仅能帮助学生巩固数的组成,而且能引导学生利用数的读写与数的组成的一致性,自然而然地学会读数、写数。
3.用算盘记数,学习数的读写
算盘是我国古代的伟大发明之一。算盘上1颗算珠的含义比计数器上1颗珠子的含义更丰富。算珠在下档表示“1”,在上档则是“以1当5”。如果不确定个位,就无法确定算珠表示的数的大小;确定个位后,1颗算珠不仅能表示1个一、1个百等,还能表示1个十分之一、1个百分之一等。与计数器相比,算盘上的两颗算珠能拨出更多的数。教师指导学生使用算盘记数、辅助数的读写,既有利于数学文化的渗透,又能为学生认识数位、体会位值制提供好的工具和途径。
三、迁移认数经验,理解运算的理与法
2022年版义务教育数学课程标准将小学“数与代数”领域内容设计为“数与运算”和“数量关系”两个主题。其中,“数与运算”包括“数的认识”和“数的运算”两个部分。这样设计旨在使学生整体理解数与数的运算。如何帮助学生学会用整体的、联系的、发展的眼光看问题,建立能支撑后续学习的结构化数学知识体系呢?
第一,用计数单位贯通数的认识和运算。运算的实质是计数单位的累加、递减及分解与组合。数的认识和数的运算有密切联系,教师应基于计数和运算的一致性、连贯性,抓住“计数单位”这个核心概念,充分利用学生认识数的经验教学四则运算。无论是整数运算还是小数、分数运算的教学,教师都要引导学生借助认数工具、通过具体操作感受计数单位个数的变化,进而理解算理、归纳算法。
第二,用计数单位贯通整数、小数和分数的运算。一方面,整数计数单位和小数计数单位都是十进制关系,在十进制数位顺序表中是连续递增(递减)排列的,教师可以引导学生将学习整数的认识和运算的经验迁移到学习小数的认识和运算中;另一方面,教师可以把分数加减运算中的通分上升到统一分数单位的高度,可以借助数形结合等思想方法帮助学生理解分数乘除法本质上同样是基于分数单位的运算,还可以将小数化为十进分数后教学小数乘除法。
责任编辑 刘佳
