关于情境真实性的理解

夏小刚　张晶

一、强调情境真实性的重要意义

2022年5月，国家发布了《义务教育数学课程标准（2022年版）》（以下简称“课程标准”）。2022年版课程标准的亮点是“强化育人导向”“培育核心素养”。在素养导向的课程目标下，课程标准提出了帮助学生“在探索真实情境所蕴含的关系中，发现问题和提出问题，运用数学和其他学科的知识与方法分析问题和解决问题”的基本要求。“真实情境”成为此次颁布的课程标准中的一个关键词，“真实性”成为情境的重要属性和情境创设的基本要求。

应该说，我们对情境是学生素养发展的重要载体已经形成共识。相应地，生活情境、现实情境、具体情境、实际情境不断进入数学教学情境创设的视野中。这种“生动”的教学场景，催生了我们的反思：为什么情境的真实性被课程标准如此重视呢？思考这个问题的关键在于“核心素养”。核心素养是确定课程目标的立足点，教师要帮助学生逐步达成“会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界”的目标，就必须通过问题和情境搭建联系学生与现实世界的桥梁。

思维是素养的核心，思维以知识为基础。正如南京师范大学喻平教授所言，学生数学核心素养的生成源于对数学知识的学习。然而，教师在教学中更习惯于把数学的概念、定理、公式从产生它们的具体情境中抽取出来，然后加以讲解并辅之以纯粹的技巧性训练。这种做法不利于激发学生的学习动机、学习情感和学习兴趣。从更深的层次来看，由于知识脱离了它赖以发生的真实情境，导致了知识迁移的“呆滞”。

知识具有“境脉性”，也就是将数学知识的教与学置于一个情境脉络之中，是知識的本性所决定的。因此，知识的问题化，以及问题的思考性与情境的真实性互嵌，有助于学生在获取知识、技能和思维方式的同时，领会应用知识、技能和思维方式的情境化条件，进而发展数学素养。

二、对情境真实性的认识与反思

真实情境是一个教师熟知却又认识模糊的问题。一方面，它与汉语中“真实”的释义有关;另一方面，它涉及对教学活动中“真实性”含义的理解。

在汉语中，“真实”是“真”与“实”的并列词组。“真”的本义是本质、本性，引申为真实，又指明确、清楚;“实”的本义是富裕，引申为事实，还指实在、真实。《现代汉语词典》把“真实”释义为“跟客观事实相符合;不假”。换言之，只要对事物的理解和认知与事物本身具有一致性，这样的认识就达到了“真”。

一段时间以来，囿于“符合论”的真实观的影响和制约，我们对情境真实性的认识陷入了数学问题与客观现实的“镜像”嵌入中。一名教师在教学“一元一次方程的应用”时，为了从生活场景中引入顺流、逆流的数学问题，创设了这样的问题情境：同学们，今天我带大家一起去郊游（音乐响起，多媒体播放美丽的野外风光，约8分钟）。随后，该教师问学生看到了什么。学生沉思片刻，有的说看见了飞翔的小鸟，有的说看见了茂密的森林。这种“去数学化”的情境设计，偏离了教学的原有目标。究其原因，除了情境设计过于花哨，还与数学教学面临的现实困境——与现实世界隔离有关。在这种困境下，学生既不能充分运用生活中的既有经验，也难以将数学学习经验迁移到“拟真”的问题情境中。

当前，数学教学面临的一个急迫任务是，培养学生有效运用数学知识解决真实的复杂情境中的问题的能力。数学教育与现实世界的隔离已成为制约学生素养发展的影响因素，因此对情境真实性的认识与反思，既是对落实信息时代教育使命的响应，也是对核心素养导向的课程目标与要求的回应。

三、情境“真实性”的理解维度

打破数学教育与现实世界的隔离，是培养学生核心素养的关键举措之一。教师需要立足于学生的内在体验，引入真实情境，设计有意义的数学问题，以此唤起学生的问题探究意识，搭建联系学生经验世界与现实世界的桥梁。

对此，课程标准在“实施促进学生发展的教学活动”的课程理念下，提出了“引导学生在真实情境中发现问题和提出问题，利用观察、猜测、实验、计算、推理、验证、数据分析、直观想象等方法分析问题和解决问题”的教学要求。进一步地，通过分析和整合课程标准的相关要求，可以发现课程标准在课程理念、课程目标、课程内容、教学建议、评价建议中多次提到“真实情境”。概括起来，大致分三种情况：一是把真实情境作为贴近学生现实、反映数学现实存在的表现形式;二是把真实情境作为激发学生发现问题、提出问题和解决问题的活动载体;三是把真实情境作为数学化的活动对象。从中可以发现，情境的真实已逐渐超越了客观事物本身的真实，成为对学生生活现实、数学活动与思维活动中的真实问题的“拟真”。此种理解下，情境的真实性有三种具体的表现形式，即经验式“真实”、理性式“真实”以及思辨式“真实”。

1.经验式“真实”

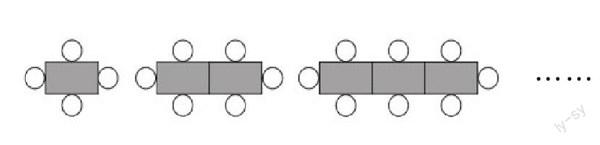
经验式“真实”就是基于经验、体现“在场”和“可见”的真实，通常可以通过对接学生的生活经验，将数学问题嵌入经验性情境中，使之“接近”学生认知，进而赋予学生一种真实性的感知——在场的真实感。笔者呈现一个“座位问题”：如下图，一张餐桌可坐4人，两张餐桌拼在一起可坐6人，三张餐桌拼在一起可坐8人，按这样拼下去，n张餐桌拼在一起可坐多少人？

该情境旨在让学生经历用字母表示变化规律的过程，培养学生的符号意识。题目中，“座位”是学生生活世界中的经验对象，其所蕴含的数量关系是学生熟知的：拼接的桌子每多1张，可坐的人数就多2人。由此形成了情境的“激发”功能。这种经验对象和数学认识，使“座位”情境具有了可感知的真实性，促进了学生对其等量关系的认识，如“可坐人数=4+（拼接的桌子数-1）×2”或“可坐人数=2+拼接的桌子数×2”等，进而形成等量关系的代数符号表示。

可见，经验式“真实”尽管不具有绝对的、普遍性的抽象意义，但紧密关联学生的经验，能为学生的境脉化学习提供条件。

2.理性式“真实”

理性式“真实”强调通过观察获得对事物的认知，重视通过理性反思对所搜集的信息予以甄别，即依据自然知识对事件或材料的真假做出理性判断。这种对真实的理解，突出了以自然知识作为判断材料，摆脱了经验判断的主观性，体现了人在“真实”表达中的理性思考。

下面呈现一个“大象称重”的问题情境：通过“曹冲称象”的故事思考两个问题，一是“在古代，为什么大象的体重难称量？”二是“要称量大象的体重，需要哪些条件？”

设计此情境，旨在帮助学生认识物体的质量，感悟质量的度量方法，并尝试运用等量的等量进行推理。众所周知，“曹冲称象”是一个出自《三国志》的历史故事，讲的是曹冲五六岁时所具备的知识和判断能力就如同一个成年人，他用许多石头代替大象，在船舷上刻记号，让船上的石头与船上的大象产生等量的效果，再一次一次称出石头的重量，使“大”转化为“小”，分而治之，使“大象称重”的难题得到圆满解决。对学生而言，“曹冲称象”的情境是可信的，具有真实性。这种真实性不仅在于可以借助专家的史料考证和实地考察进行判断，更重要的是，在大象称重中，曹冲采用的“等量替换法”所蕴含的“等量的等量相等”的基本事实，为情境的真实性提供了佐证。

3.思辨式“真实”

思辨式“真实”强调情境所反映的对人类行为普遍性的认识。“在场”不一定能把握真相，“见证”不一定看得到事情的全部，加上生命的有限性与时间的“一维性”，我们不一定能获得对事实本身的把握，并以此作出是否真实的判断。因此，教师将数学知识、科学知识及人文知识作为情境的背景信息，以此给学生提供数学学习的真实感，能使学生在感知数学的过去的同时，认识数学的未来。

下面呈现一个问题情境：有一个长方形，想象让这个长方形分别以长边和短边所在直线为轴旋转得到两个圆柱，猜想哪个圆柱的体积更大。

该情境是一个典型的数学情境，旨在帮助学生通过实例感悟推理过程的逻辑性，包括通过归纳推理得到结论的过程的逻辑性，以及通过演绎推理验证结论的过程的逻辑性。其背景信息不仅嵌入了长方形、圆柱等几何要素，渗透了旋转变换关系，而且蕴含了圆柱的体积V与圆柱底面半径r和圆柱的高h之间的数学关系——[V=πr2h]。特别是两种不同形式的旋转，使情境具有了激活学生数学思维的作用。该情境因其蕴含的数學关系而具有了“真实性”。学生不仅因此在学习中可以对接已有的知识经验，而且被赋予了体验数学探究的机会。

当下，一个值得关注的重要话题是：如何促进核心素养落地，为知识运用赋能。无疑，实现情境的真实性，其重要性不言而喻。然而，对情境真实性的正确理解，或许更有助于我们在情境真实性与问题思考性的有机互嵌中，把握问题情境化背后所蕴含的学习隐喻的变化，促进问题情境化设计由服务于“外在的认识”转向注重“内在的体验”，进而发展学生的核心素养。

[本文系全国教育科学“十三五”规划课题“面向核心素养的数学问题情境教学测评模型研究”的研究成果。课题编号：XHA180286]

责任编辑  刘佳

夏小刚

贵州师范大学数学科学学院教授、博士生导师、副院长，教育部高等学校数学类专业教学指导委员会委员;已在《比较教育研究》《数学教育学报》《人民教育》《民族教育研究》《课程·教材·教法》《数学通报》《Journal of Mathematics Education》等期刊发表“数学情境的创设与数学问题提出”等论文，出版《基于提出问题的数学教学研究》等著作;曾获国家级教学成果一等奖等奖励，以及贵州省高等学校教学名师、贵州省优秀教师等荣誉称号。