基于“APOS”理论的小学数学深度实验

王雨婷

数学知识的基本元素就是概念。“APOS”理论（包括活动Action、过程Process、对象Object和图式Schema四个阶段）是由美国学者杜宾斯基提出的关于数学概念学习的理论。他认为人是不可能直接学习到数学概念的，需要透过心智结构才能使所学的数学概念产生意义。对于学习者而言，该理论强调的是在学习新知识之前，要对所学的内容进行充分的预设，学习者需要通过主动建构来获得知识。

“APOS”理论下的“圆的面积”数学实验，可以使学生在活动中体验，在过程中压缩，将对象重置，从而形成图式，帮助学生更好地体会图形变化中的无限逼近数学思想，深入理解圆的面积公式。

一、实验活动设计—基于“原形”的反向推演

“活动”是“APOS”理论的第一阶段。数学学习离不开数学活动，操作运算行为是数学认知基础性行为。对于小学生来说，许多数学思考是隐性的，不容易发现，需要通过一系列的显性的探索活动来实现。在进行活动设计时，教师需要考虑学生能够到达的层次，并根据层次来推演基于怎样的“原形”才能达成。

1. 基于“原形”的深度研判

在这里，“原形”不是简单的知识内容，而是内容的知识原形，是学生的认知原形。要进行圆的面积探究的活动设计，就要知道这个知识是怎样形成的。“圆的面积”知识原形可分为两部分：一是极限转化，将一个圆平均分成若干个扇形，然后拼成一个平行四边形，经历不断细化的拼接，使得平行四边形逐渐趋向长方形，最终通过极限思想下的转化将圆的面积与长方形的面积画上等号，得到圆的面积公式。二是圆的面积与圆半径的平方之间的倍数关系，即圆的面积与以圆的半径为边长的正方形面积的倍数关系，这一量与量之间的关系，也是圆的面积运用的原形。

2. 已有图式与经验的深度研判

在探究圆的面积之前，学生已经对圆有了一定的认识，知道圆的特征、半径、弧长等知识，经历过长方形、正方形、平行四边形等圖形面积的推导过程，对“割补”“转化”等数学方法与数学思想有过感受。同时，学生在之前学习“积的变化规律”“找规律”等时，经历过量与量之间关系的探索过程，积累了一定的活动经验。

3. 实验方式的深度研判

从学习的角度出发可知：学生对于倍数关系比较熟悉，但对于一个范围内的倍数关系（π倍）还比较陌生，需要一定的操作积累和抽象推理。极限转化学生是第一次接触，无论在直观感知上还是抽象理解上都存在建构支撑的空白，同样需要经历动手操作和思维操作的结合。

以此研判为依据，实验操作可以分为两层：一是提供方格纸的分层次操作实验，以数方格算倍数的方式达成对倍数范围的感知;二是提供圆形纸片及分割思路，将圆形纸片分成小扇形进行拼接，感知图形的极限转化，然后进行量化对比，得出圆的面积的计算方法。

二、实验操作过程—从现象到信息的累积

“过程”是“APOS”理论的第二阶段。学生在“活动”中对“活动”进行思考，思维逐渐获得内化并压缩，这样的“活动”经过多次重复后，就可以内化并稳固为一种“过程”性的心理活动。不是一次操作就能达成，而是需要反复、多次的操作，获得更多的数据与信息，为下一步的思考、再操作奠定基础。

1. 物理感知的抽象积累

向学生呈现一个以正方形的边长（4cm）为半径画的圆，教师指导学生用数方格的方法来计算圆的面积，先数出四分之一个圆，有接近12个整格，约3个半格，其中3个半格的面积加起来可以大约看作1整格，因此可以看作共13个整格，圆的面积是52cm?，并将所得到的结果填入表1。

在这样的操作活动后，学生掌握了基本的操作方法。教师再出示以5cm、6cm的正方形的边为半径画的圆，学生独立操作，通过直接计算来推演圆的面积大约是正方形面积的多少倍（见表1）。

表1 圆的面积与正方形面积的关系

正方形的面积（cm2） 圆的半径（cm） 圆的面积（cm2） 圆的面积大约是

正方形面积的几倍

16 4 52 3.3

25 5 76 3.0

36 6 112 3.1

这一组操作实验给学生带来的是物理现象的感知。结合数据信息，学生对物理感知进行数学化的抽象分析，体验到了圆的面积与边长为r的正方形面积之间的倍数关系。这个关系虽然是个范围，但是给学生带来的体验是真实的，也启发学生将这个倍数与π之间产生积极的联系。

2. 形象感知的抽象推进

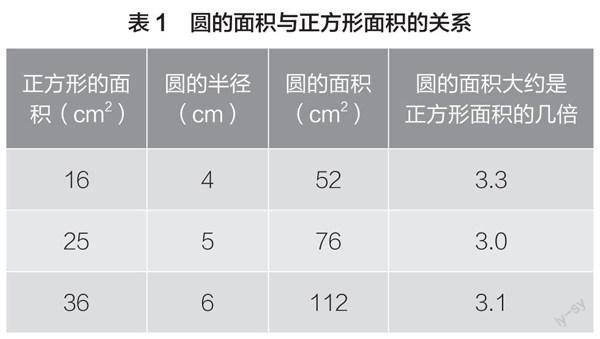
在教师的指导下，学生进行第二个操作活动，将一个圆形纸片进行16等分，再拼一拼，看看能拼成什么图形，并汇报（见图1）。

图1 把圆16等分并拼图

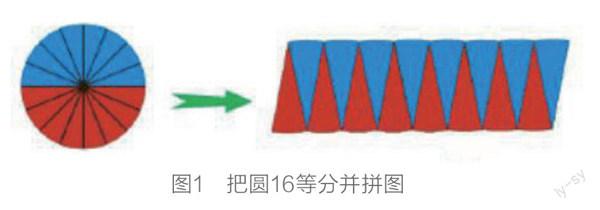
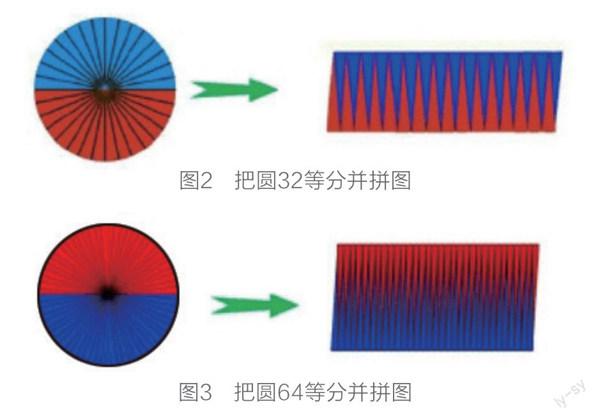
教师通过多媒体演示把圆平均分成32份、64份并拼图的过程（见图2、图3），引导学生观察并分析，与图1比较拼成的图形发生了哪些变化。

图2 把圆32等分并拼图

图3 把圆64等分并拼图

圆是小学数学阶段最后学习的平面图形，具有它的特殊性—唯一一个曲线图形。本课的学习内容比较抽象，之前的学习经验并不能直接迁移到本课的学习中来，学生通过自己的实际操作进行感知，符合他们的认知水平和能力。

三、实验内化压缩—对象的重置与反演

“对象”是“APOS”理论的第三阶段。这时概念已经被形式化、抽象化，成了新的具体的对象，以此开展新的“活动”。这里的“对象”不是指学习者，而是指实验中得到的数据与信息，涉及一个“脱身”的概念，学习者从旁观者的角度来看之前的操作过程，客观进行操作发现。

1. 抽象感知的概括

在物理操作中，学生积累了丰富的抽象感知，同时，学生也能通过自己的感知对数学发现进行简单概括：在第一个操作活动中，根据自己已有的认知水平和活动经验，知道正方形的面积就是圆半径的平方，在此基础上，了解正方形面积与圆面积的关系就是圆的半径平方与圆面积之间的关系。在第二个操作活动中，学生发现随着圆平均分的份数增多，所拼成的图形越来越趋向于长方形，发现从圆到长方形，形状变了，但是面积没有改变，从而建立圆的面积与长方形的面积的联系，感受极限思想下的转化，为下一阶段做准备。

2. 概念的数学表达

学生通过探究圆的面积的过程，能充分地运用口头语言及书面语言对可操作的对象进行解释。教师鼓励学生积极、主动地交流，用语言表达他们的数学理解。

在第一个操作活动中，学生通过数格子和计算，将数据填写在表格中，通过对数据的观察与分析，再加上之前的自主探索，能发现圆的半径平方与圆面积之间的倍数关系。数学表达有书面表达和语言表达两种，活动到了这一阶段，书面表达对于大部分学生来说都不是难事，学生通过表格中的数据，能写出量与量之间存在的倍数关系。语言表达需要学生通过对整个操作活动的回顾与反思，自然地说出圆的面积是圆半径平方的3倍多一些。同样，在第二个操作活动中，教师可以请学生说说得到了怎样的图形，学生回答：“得到一個近似长方形的图形，这个图形的长是圆周长的一半，可以用πr表示，宽就是圆的半径r，因为长方形的面积是长×宽，所以圆的面积可以写成πr（长）×r（宽），即πr?。”

四、实验的顺应—图式的迁移应用

“图式”是“APOS”理论的第四阶段。图式是较为稳定的认知模型，在长期的学习活动中不断被完善，起初只是反映概念的特例、抽象过程、定义形态，后来学习者将概念与其他概念建立起内在的联系，在大脑中形成较为稳定的、综合的认知结构。

1. 实验的图式内化

学生在上一阶段已经可以进行数学表达，那么图式的形成就水到渠成了。第一个操作活动学生知道圆的面积是圆半径平方的3倍多，第二个操作活动学生从长方形的面积推导出圆的面积公式，体现了极限思想下的转化。在已有图式的基础上，学生形成了新的图式。

2. 图式的迁移运用

图式的形成只是第一步，还需要学生能够灵活运用，教师可以通过习题的设计来达成迁移运用的目标。以下练习题，目的是让学生体会面积之间的关系，再次感受极限思想下的转化在数学中的应用。

习题：把圆平均分成16份，拼成一个三角形，推导圆的面积公式。

值得一提的是，“APOS”理论下的深度实验并不是一个线性过程，而是一个循环过程。在探究圆的面积时，通过活动、过程、对象、图式，我们知道了圆的面积是半径平方的3倍多，但要具体探究这个3倍多究竟是多少，就要在一个新的实验中重新经历这四个阶段，在反复循环中形成真正的图式。

（作者单位：江苏省苏州市吴江区盛泽实验小学）

责任编辑：赵继莹