利用中点条件 寻找解题思路

王卫胜

考题再现

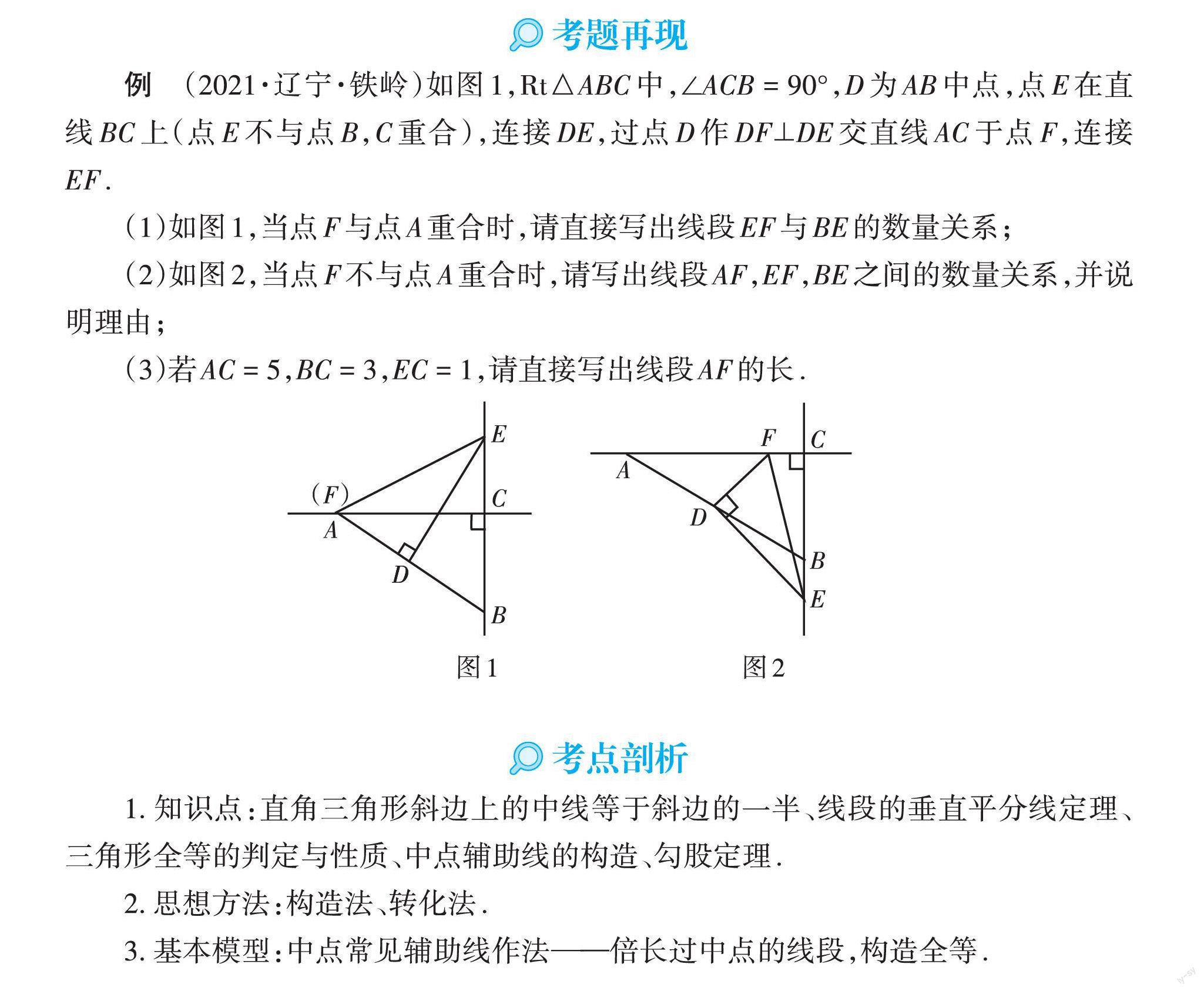
例 （2021·辽宁·铁岭）如图1，Rt△ABC中，∠ACB = 90°，D为AB中点，点E在直线BC上（點E不与点B，C重合），连接DE，过点D作DF⊥DE交直线AC于点F，连接EF.

（1）如图1，当点F与点A重合时，请直接写出线段EF与BE的数量关系;

（2）如图2，当点F不与点A重合时，请写出线段AF，EF，BE之间的数量关系，并说明理由;

（3）若AC = 5，BC = 3，EC = 1，请直接写出线段AF的长.

考点剖析

1. 知识点：直角三角形斜边上的中线等于斜边的一半、线段的垂直平分线定理、三角形全等的判定与性质、中点辅助线的构造、勾股定理.

2. 思想方法：构造法、转化法.

3. 基本模型：中点常见辅助线作法——倍长过中点的线段，构造全等.

学情分析

解题思路：（1）根据DE垂直平分AB，可得出EF = BE.

（2）三条线段的数量关系包括和差关系和平方关系，本题是后者.需要把三条线段转化在同一个直角三角形内. 因为题中有中点，因此很容易想到解决中点问题的通法——倍长过中点的线段来构造全等. 故延长ED至点G，使DG = ED，再连接AG，FG，即可将三条线段转化在Rt△AFG中，如图3.

解：（1）∵D为AB中点，DF⊥DE，

∴DE为AB的垂直平分线，∴EF = BE.

（2）结论：AF2 + BE2 = EF2.

理由：如图3，过点A作AG⊥AC，交ED的延长线于G，连接FG.

∵AG⊥AC，EC⊥AC，

∴AG[?]BE，∴∠AGD = ∠BED.

在△AGD和△BED中，

[∠AGD=∠BED，∠ADG=∠BDE，AD=BD，]

∴△AGD ≌ △BED（AAS），

∴AG = BE，DG = DE.

∵DF⊥EG，∴FG = EF.

∵∠FAG = 90°，∴AF2 + AG2 = FG2，

∴AF2 + BE2 = EF2.

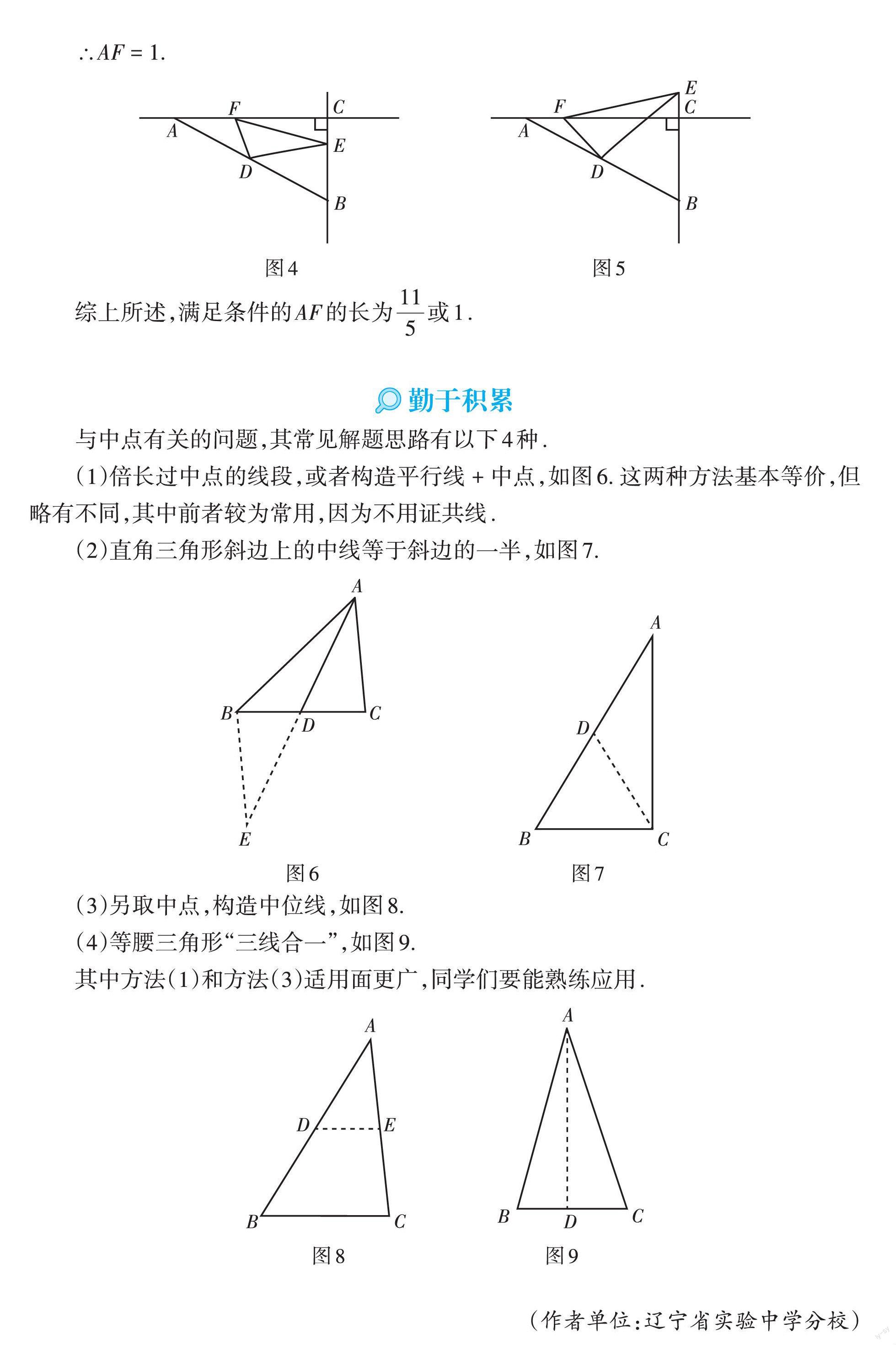
（3）EC = 1是一个重要的隐含条件，点E可以在线段BC上，也可以在线段BC的延长线上，可继续倍长过中点的线段构造全等来解决问题.

如图4，当点E在线段BC上时，

设AF = x，则CF = 5 - x.

∵BC = 3，CE = 1，∴BE = 2，

∵EF2 = AF2 + BE2 = CF2 + CE2，

∴x2 + 22 = （5 - x）2 + 12，

∴x = [115]，∴AF = [115].

如图5，当点E在线段BC的延长线上时，

设AF = x，则CF = 5 - x.

∵BC = 3，CE = 1，∴BE = 4，

∵EF2 = AF2 + BE2 = CF2 + CE2，

∴x2 + 42 = （5 - x）2 + 12，∴x = 1，

∴AF = 1.

综上所述，满足条件的AF的长为[115]或1.

勤于积累

与中点有关的问题，其常见解题思路有以下4种.

（1）倍长过中点的线段，或者构造平行线 + 中点，如图6. 这两种方法基本等价，但略有不同，其中前者较为常用，因为不用证共线.

（2）直角三角形斜边上的中线等于斜边的一半，如图7.

（3）另取中点，构造中位线，如图8.

（4）等腰三角形“三线合一”，如图9.

其中方法（1）和方法（3）适用面更广，同学们要能熟练应用.

（作者单位：辽宁省实验中学分校）