重创新、重应用,引领数学进入新时代

许少华

“学好数、理、化，走遍天下都不怕”，它告诉我们“数、理、化”是一门生存绝技，你拥有它，无论到哪里，都可以立足.事实上，数理化作为基础学科，不仅对一个人重要，对国家也非常重要，我们要高科技有突破、我们要军队现代化、我们要全面进入小康，哪一点都要求数理化必须先行、必须有雄厚的基础知识与基础理论作支撑. 因此，2022年高考数学命题率先吹起了冲锋号，以重创新、重应用，引领数学进入新时代为己任，设计命制出全新的数学试题，下面让我们慢慢品味与欣赏.

一、试题的特点

1. 试题的背景材料

从1952年毛主席视察黄河时提出的“南水北调”到目前的疫情防控，横跨几十年的现实生活问题是本次的两道试题的社会背景. 从数字的大小比较、体积的取值范围到式子的最值问题，究其实质都是以不等式为背景. 同样，以函数为背景、以数形结合为背景等考题比比皆是. 明面上的问题，若离开了背景材料也许会很空洞，当然，你的求解若不联系一下背景，也许会无从下手.

2. 试题的双基覆盖面

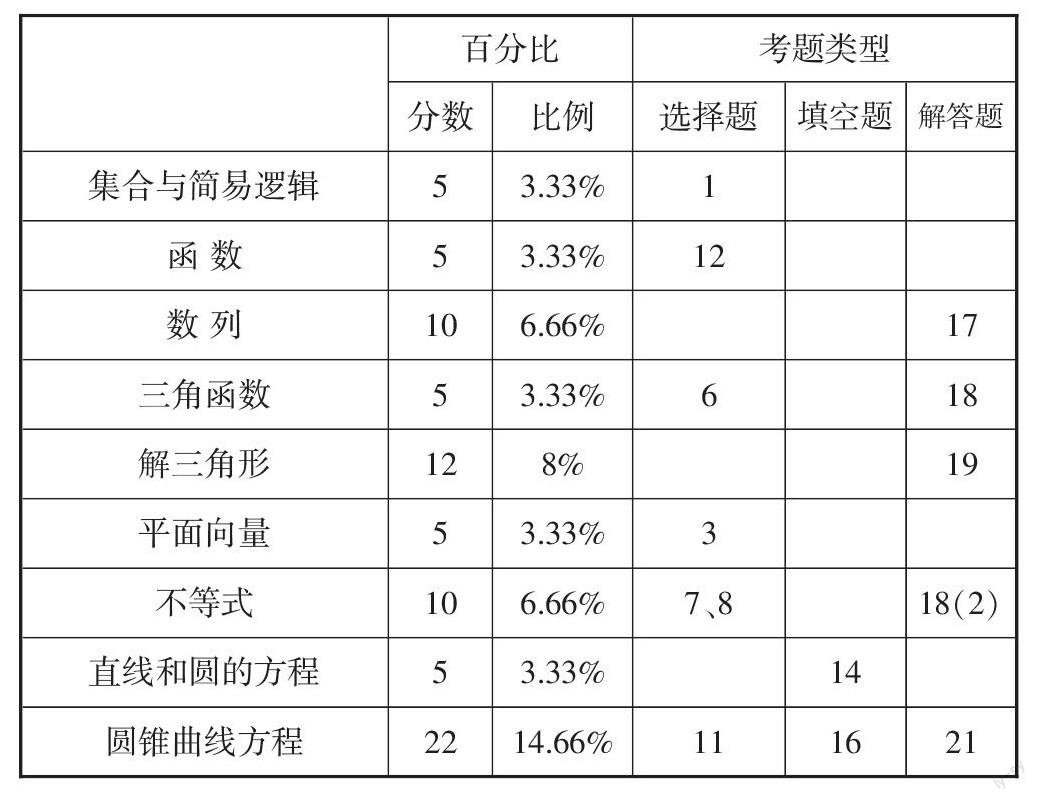
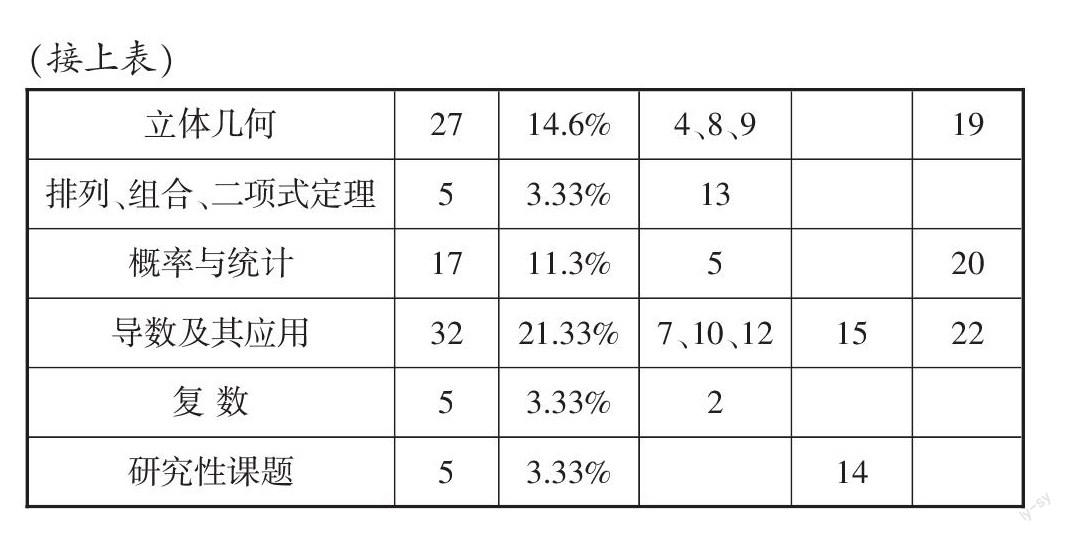
今年的高考题对知识点的覆盖情况及知识点考查时所用的题目类型见下表：

从上表可以看出：基础知识的覆盖面很广，且重点知识得到了重点考查. 如导数及其应用、圆锥曲线、立体几何等考试的分数相对较高. 当然，我们也可以看出：三角函数、基本初等函数、数列考的内容相对较少，而重点考查的内容要么比较难、要么比较繁、要么难以想象，于是，就构成了本次试题较难.

3. 对应用性的考查

试题对应用性的考查体现在三个方面：一是方法的应用，第2题“若i（1-z）=1，则z+=（ ）A. -2 B. -1 C. 1 D. 2”，对已知的式子两边同乘-i，很快便看出结论. 第3题“在ΔABC中，点D在边AB上，BD=2DA. 记=，=，则=（ ）A. 3-2 B. -2+3 C. 3-2 D. 2+3”，考查向量减法的应用，即由BD=2DA?=2?-=2（-）立得结论. 类似地应用随处可见，它强调基本方法的灵活性，注重了这些，几乎可以一望而解. 其次是技能的应用，第7 题无论是构造函数还是放缩，必备的技能你必须拥有，否则，你肯定会一筹莫展，第12题由f（3-x）=f（x）?-f′（3-x）=f′（x）??-g（3-x）=g（x）恰到好处的产生周期函数，这个技能应用得很漂亮. 第三是数学知识的应用，第4题、第5题及第20题，都要求我们应用所拥有的数学知识与技能来处理具体问题.

4. 对交汇性的考查

在知识的交汇点处设计试题，永远都是高考试题设计的重要思路之一，我们看看第6题将三角函数的图像性质与三角函数的诱导公式等相结合. 第8题立体几何的基本计算与基本不等式相结合或者与三角函数相结合. 第18题正弦定理与基本不等式相结合. 第13题的二项定理问题与排列给相结合等. 都不是孤立的，每一道题，那怕是排在前面较为基础的问题，也都会涉及多个知识点，可以说考查单一知识点或某一技能点的试题不存在，都是小综合，至少是在本知识块范围内的多个知识点联系在一起，比如第10题，考查函数的极值点、零点、对称中心、切线，“四合一”，函数还有哪些常见性质，是不是都囊括其中了，本题要想产生正确结论，哪一点不过关都不行.

5. 对创新性的考查

创新性体现两个方面，一是试题创新，这里指背景材料或试题结构，比如第14题“写出与圆x2+y2=1和（x-3）2+（y-4）2=16都相切的一条直线的方程___________.”这里仅强调一条，也就是说你写出一条就可以了，本题的两个圆的方程都是以标准方程给出，图像很好画，灵活的考生画一下立刻产生结论，难吗？因为它创新了，打破了传统的求解模式，很多同学不适应，还在循规蹈矩的计算，时间过去了，结论没产生，叹一声，这题不仅难而且很繁. 另一个是应用创新，第7题“设a=0.1e0.1，b=，c=-ln0.9，则（    ）A. a

6. 对数学核心素养的考查

数学核心素养包括六个方面：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析. 本次考试对核心素养的考查可谓是力度空前. 第7题、第12题对抽象能力的要求较高. 第20题的第一问与第22题求解的逻辑推理相当严谨. 数学运算包含字母运算与数字运算，看看第4题与第8题不仅要有运算的耐心与自信心，更要注重运算的合理性与科学性，再看看三道圆锥曲线试题（即第11题、第16题与第21题），那一道都不是“省油的灯”，既要注重常规方法与技巧，又要因条件、因结论适时转化与调整，说难不为过、说繁也不为过. 直观想象与数据分析活活的被联想、分析、运算、推理所淹没.

7. 整套试卷的难易度

“本手、妙手与俗手，不如数学无从下手”“不管什么手，考完数学当X团骑手”，这虽是网络语不足为奇，但回到理性角度看，纵向看：今年要比前几年都难很多（今年至此时并未公布全省平均分，虽有前几年的分数，但无法进行比较，这里还带有几分感性色彩）. 横向看：某班语文老师在家长群发微信说，到目前已知道了我们班最高分129分，平均分超過110分，家长一片赞誉. 英语老师也在家长群发微信说，全级140分以上的81人，最高分147分，有六个班平均分130分以上.“英语老师个个都厉害”. 我们呢？不厉害吗？不努力吗？不拚吗？结果让我们只有沉默，望着众多的几十分，甚至更可怜的分数发呆.

既然数学是基础学科、既然希望全民重视数学，高考结束，要让考生可以感觉到“数学好，才是真的好”“成也数学，败也数学”，它对试题的要求不是难，而是有很好的区分度，它向一把量尺，把学生进行三六等进行科学地分类，而这个分類足以影响整个高考成绩.

重创新、重应用、重核心素养的考查本是好事，值得点赞. 但一定要清楚，这些考查不是仅有难题才能体现，高考，不是掐尖、也不是竞赛. 当大家的分数都聚集在某些分数段之间时，选拔失去了准确性. 对以后的数学学习都是不利的，它损害了自信心，让一些基础一般的考生丧失了攻克数学的勇气与决心.

二、好题妙解欣赏

1. 第7题：设a=0.1e0.1，b=，c=-ln0.9，则（ ）

A. a

解与评 设f（x）=ln（1+x）-x（x>-1），因为f′（x）=-1=  -，当x∈（-1，0）时，f′（x）>0，当x∈（0，+∞）时f′（x）<0，所以函数f（x）=ln（1+x）-x在（0，+∞）单调递减，在（-1，0）上单调递增，所以f（-）a.

或者：令f（x）=ln（xex）-ln（0

由于f′（x）=1-=-<0，所以f（x）在（0，0.1）上递减.又f（0）=0，于是f（0.1）<0，即ln（0.1e0.1）-ln<0?0.1e0.1a.

又或者：借助ex>x+1，由==e0.1>（1-0.1）=1?b>a.

设g（x）=xex+ln（1-x）（00，函数h（x）=ex（x2-1）+1单调递增.

又h（0）=0，所以当00，函数g（x）=xex+ln（1-x）单调递增，所以g（0.1）>g（0）=0，即0.1e0.1>-ln0.9，所以a>c.

故选：C.

2. 第8题：已知正四棱锥的侧棱长为l，其各顶点都在同一球面上. 若该球的体积为36π，且3≤l≤3，则该正四棱锥体积的取值范围是（ ）

A. 18

， B.

， C.

， D. [18，27]

解与评 C. ∵ 球的体积为36π，所以球的半径R=3，设正四棱锥的底面边长为2a，高为h，则l2=2a2+h2，又由32=2a2+（3-h）2，得6h=l2，2a2=l2-h2.

体积V=Sh=×4a2×h=×（l2-）×=（l4-），由V′=（4l3-）=l3（），

当3≤l≤2时，V′>0，当2

，.

或者：设四棱锥的高与侧棱夹角为θ，高为h，底面中心到各顶点的距离为m，则cosθ==.

由3≤l≤3，得cosθ∈[，]，则l=6cosθ，m=lsinθ=6cosθsinθ，h==6cos2θ，

于是V=×2m2h=144（sinθcos2θ）2.

令x=sinθ，则x∈[，]，y=x（1-x2），x∈[，]得≤y2≤?≤V≤.

难吗？不算难. 好做吗？实在不好做，有思路与有正确结论是两码事. 你能想到，你可能根本就做不到. 运算能力与运算的自信心在这里受到了严重的挑战.

3. 第10题：已知函数f（x）=x3-x+1，则（ ）

A. f（x）有两个极值点

B. f（x）有三个零点

C. 点（0，1）是曲线y=f（x）的对称中心

D. 直线y=2x是曲线y=f（x）的切线

解与评 AC. 由题，f′（x）=3x2-1，令f′（x）>0得x>或x<-，令f′（x）<0得-

所以f（x）在（-，）上单调递减，在（-∞，-），（，+∞）上单调递增，故x=±是极值点，故A正确.

因f（-）=1+>0，f（）=1->0，f（-2）=-5<0，所以，函数f（x）在（-∞，-）上有一个零点，当x≥时，f（x）≥f（）>0，即函数f（x）在（，+∞）上无零点，此时，函数f（x）有一个零点，故B错误.

令h（x）=x3-x，该函数的定义域为R，h（-x）=（-x）3-（-x）=-x3+x=-h（x），则h（x）是奇函数，（0，0）是h（x）的对称中心，将h（x）的图像向上移动一个单位得到f（x）的图像，所以点（0，1）是曲线y=f（x）的对称中心，故C正确.

令f′（x）=3x2-1=2，可得x=±1，又f（1）=f（-1）=1，当切点为（1，1）时，切线方程为y=2x-1，当切点为（-1，1）时，切线方程为y=2x+3，故D错误.

本题将函数f（x）=x3-x+1的所有性质几乎都考了一遍，有一个地方不清楚，也不可能产生正确结论.

4. 第11题：已知O为坐标原点，点A（1，1）在抛物线C∶x2=2py（p>0）上，过点B（0，-1）的直线交C于P，Q两点，则（ ）

A. C的准线为y=-1    B. 直线AB与C相切

C. OP·OQ>OA2     D. BP·BQ>BA2

解与评 BCD. 将点A的代入抛物线方程得1=2p，所以抛物线方程为x2=y，故准线方程为y=-，A错误.

由kAB==2，所以直线AB的方程为y=2x-1，联立y=2x-1，

x2=y，可得x2-2x+1=0，解得x=1，故B正确.

设过B的直线为l，若直线l与y轴重合，则直线l与抛物线C只有一个交点，所以，直线l的斜率存在，设其方程为y=kx-1，P（x1，y1），Q（x2，y2），联立y=kx-1，

x2=y，得x2-kx+1=0，所以Δ=k2-4>0，

x1+x2=k，

x1x2=1，所以k>2或k<-2，y1y2=（x1x2）2=1. 又OP==，OQ==，所以OP·OQ===k>2=OA2，故C正确.

因为BP=x1，BQ=x2，所以BP·BQ=（1+k2）x1x2=1+k2>5，而BA2=5，故D正确.

5. 第12： 已知函数f（x）及其导函数f′（x）的定义域均为R，记g（x）=f ′（x），若f（-2x），g（2+x）均为偶函数，则（ ）

A. f（0）=0  B. g（-）=0  C. f（-1）=f（4）  D. g（-1）=g（2）

解与评 BC. 因為f（-2x），g（2+x）均为偶函数，所以f（-2x）=f（+2x）即f（-x）=f（+x），g（2+x）=g（2-x），所以f（3-x）=f（x），g（4-x）=g（x），则f（-1）=f（4），故C正确.

函数f（x），g（x）的图像分别关于直线x=，x=2对称，又g（x）=f ′（x），且函数f（x）可导.

所以g（）=0，g（3-x）=-g（x），所以g（4-x）=g（x）=-g（3-x），所以g（x+2）=-g（x+1）=g（x），

所以g（-）=g（）=0，g（-1）=g（1）=-g（2），故B正确，D错误.

若函数f（x）满足题设条件，则函数f（x）+C（C为常数）也满足题设条件，所以无法确定f（x）的函数值，故A错误.

本题将f（x）与f ′（x）联合设计抽象函数问题，可谓思维独到，特别由f （3-x）=f（x）?-f ′（3-x）=f ′（x）?-g（3-x）=g（x）更是难以想象. 很高深吧？不是. 但绝对是“出其不意”，这就是设计的“精妙”与“高超”之处.

6. 第15：若曲线y=（x+a）ex有两条过坐标原点的切线，则a的取值范围是______________.

解与评 （-∞，-4）∪（0，+∞）. ∵ y=（x+a）ex，∴ y′=（x+1+a）ex，设切点为（x0，y0），则y0=（x0+a）[ex][0]，切线斜率k=（x0+1+a）[ex][0]，切线方程为：y-（x0+a）[ex][0]=（x0+1+a）[ex][0]（x-x0），∵切线过原点，∴ -（x0+a）[ex][0]=（x0+1+a）[ex][0]（-x0），整理得：[x2][0]+ax0-a=0，∵切线有两条，∴ Δ=a2+4a>0，解得a<-4或a>0，∴ a的取值范围是（-∞，-4）∪（0，+∞）.

本题有点特别，想一想去年的第7题“若过点（a，b）可以作曲线y=ex的两条切线，则（ ）A. eb

7. 第16：已知椭圆C∶+=1（a>b>0），C的上顶点为A，两个焦点为F1，F2，离心率为. 过F1且垂直于AF2的直线与C交于D，E两点，DE=6，则△ADE的周长是______________.

解与评 ∵椭圆的离心率为e==，∴ a=2c，∴b2=a2-c2=3c2，∴椭圆的方程为+=1，即3x2+4y2-12c2=0. 不妨设左焦点为F1，右焦点为F2，如下图，∵ AF2=a，OF2=c，a=2c，∴∠AF2O=，∴△AF1F2为正三角形. ∵过F1且垂直于AF2的直线与C交于D，E两点，DE为线段AF2的垂直平分线，∴ 直线DE的斜率为，斜率倒数为， 直线DE的方程：x=y-c，代入椭圆方程3x2+4y2-12c2=0，整理化简得到：13y2-6cy-9c2=0，判别式Δ=（6c）2+4×13×9c2=62×16×c2，

∴CD=y1-y2=2×=2×6×4×=6，∴ c=，得a=2c=.

∵ DE为线段AF2的垂直平分线，根据对称性，AD=DF2，AE=EF2，∴ △ADE的周长等于△F2DE的周长，利用椭圆的定义得到△F2DE周长为：

DF2+EF2+DE=DF2+EF2+DF1+EF1=DF1+DF2+EF1+EF2=2a+2a=4a=13.

本题利用离心率得到椭圆的方程为+=1，即3x2+4y2-12c2=0，根据离心率得到直线AF2的斜率，进而利用直线的垂直关系得到直线DE的斜率，写出直线DE的方程：x=y-c，代入椭圆方程3x2+4y2-12c2=0，整理化简得到：13y2-6cy-9c2=0，利用弦长公式求得c=，得a=2c=，根据对称性将ΔADE的周长转化为△F2DE的周长，利用椭圆的定义得到周长为4a=13. 思路很常规，难度也不算大，但一步一步地走下来真的很费时间.

8. 第22题：已知函数f（x）=ex-ax和g（x）=ax-lnx有相同最小值.

（1）求a.

（2）证明：存在直线y=b，其与两条曲线y=f（x）和y=g（x）共有三个不同的交点，并且从左到右的三个交点的横坐标成等差数列.

解与评 （1）由f（x）=ex-ax的定义域为R，而f′（x）=ex-a，若a≤0，则f′（x）>0，此时f（x）无最小值于是a>0. 当xlna时，f′（x）>0，故f（x）在（lna，+∞）上为增函数，故f（x）min=f（lna）=a-alna.

g（x）=ax-lnx的定义域为（0，+∞），而g′（x）=a-=. 当0时，g′（x）>0，故g（x）在（，+∞）上为增函数，故g（x）min=g（）=1-ln.

因为f（x）=ex-ax和g（x）=ax-lnx有相同的最小值，即1-ln=a-alna，整理得到=lna，其中a>0.

设g（a）=-lna，a>0，则g′（a）=-=≤0，故g（a）为（0，+∞）上的减函数，而g（1）=0，于是g（a）=0的唯一解为a=1，故=lna的解为a=1. 综上，a=1.

（2）由（1）可得f（x）=ex-x且f（x）在（-∞，0）上为减函数，在（0，+∞）上为增函数. g（x）=x-lnx且g（x）在（0，1）上为减函数，在（1，+∞）上为增函数，由于两函数有相同的最小值1.

于是，存在x2∈（0，1），使f（x2）=g（x2）=b，此时直线y=b，与两条曲线y=f（x）和y=g（x）共有三个不同的交点，不妨设三交点分别为（x1，f（x1）），（x2，f（x2）），（x3，g（x3））

由f（x1）=g（x2）=x2-lnx2=elnx2-lnx2=f（lnx2），由于x1<0，f（lnx2）<0又f（x）在（-∞，0）上单调，所以x1=lnx2.

又f（x2）=g（x3）=x3-lnx3=elnx3-lnx3=f（lnx3），由于x2>0，f（lnx3）>0又f（x）在（0，+∞）上单调，所以x2=lnx3?x3=ex2.

再由f（x2）=g（x2）?ex2-x2=x2-lnx2?2x2=ex2+lnx2=x3+x1即从左到右的三个交点的横坐标成等差数列.

本题的第一问不算难，考生得分不高的原因是，不太常规，从本年度的模拟卷与仿真卷看，第一问一般都是讨论单调性、切线及与极值有关的问题等，往往不太复杂，但这里不同，一下子要求两个最小值，这还不算，建立在两最小值相等的基础上产生的方程，解方程时发现是超越方程，只有构造函数，通过函数的单调性与观察法相结合最终产生结论，至此，考生已筋疲力尽，再往下走，已是信心不足了. 对于第二问，它不是让我们普通人来解的，它是留给“清、北”的人，它的求解有多种方法，唯上述方法数学味最浓、也最为简捷.

三、对2023年备考的启发

命题方向发生了变化，复习策略当然也要跟着变化，再“穿新鞋走老路”变不合适了，怎么办？

1. 基础内容求熟练，稳中求新. 2023年的高考复习既要抓基础知识的全面掌握，又要注重特殊基础知识的灵活应用与变形应用. 注重细微之处设计新颖地、开放性的练习题.

2. 注重培养运算的合理性、科学性与严谨性.运算能力是中学生必须具有的重要的数学能力，本次考试充分体现了对这一重要能力的要求是高层次的. 新的一年在备考复习中要从算理入手，通过分析运算的式子或将要进行的运算的特点来设计运算思路. 不排除结合特殊内容（比如：立体几何、圆锥曲线）设计有关运算能力的特殊训练.

3. 加强知识的交汇点的复习，在知识网络的交汇点处设计试题是本次试题的一大特点. 不等式是中学数学中的重要工具，在中学数学中有着举足轻重的位置，但本次有独立的不等式题目吗？没有. 没考不等式吗？也没有. 它将不等式有效的溶解在立几中、在三角中、在函数中、在导数中、在创新型试题中. 函数是中学数学的一条主线，它贯穿于中学数学的始终、它可以渗透于中学数学的任意章节，本次考试除了明确的几道试题外，函數在其他试题中也有较好的渗透.  因此，2023年的高考复习在抓住重点知识与主干知识的同时，一定要关注它们与其它内容的交汇性. 根据知识的特点，精心设计综合性强、代表性强的交汇性练习. 让学生解一题、懂一块、熟一类，在活与变上下功夫.

4. 重视对数学思想的应用. 数学思想是数学的灵魂，是数学方法与技能实质的体现，对解题思路的产生具有指导意义. 因此，中学数学教学的一个中心就是向考生渗透各种数学思想，强化完整的数学教学过程，即思想指导过程、方法运用过程与知识形成过程，使三者和谐统一. 另外，函数思想、方程思想、换元思想也是中学数学中的重要思想在本卷中体现得明显，在2023年的复习中一定要加以重视.

5. 注重对遗漏知识点的关注，教材中的每一个教学内容都是高考的命题内容，今年未考不代表不重要，相反它在下一年被命题的可能性会大增. 结合前面的知识考查细目表，对照一下未考的或考得较少的内容，注意找准关键，加强复习.

6. 在综合复习阶段，注重知识与应用的创新性、开放性、研究性，它可能是近期一段时间高考命题的重点与热点，从本次试题看，以后高考数学在分数上要想有所突破，仅靠你记住了多少定义、定理及性质，你记住了多少二级结论，你又拥有了多少常规“武器”，肯定是不行. 信息时代下，我们的高考复习也要与时俱进，多在创新上动动“歪脑筋”.

总结过去，是为了更好地把握未来、开创未来，立足2022高考试题，希望我们能认清方向、找准方法，在新的一年有一个较好的收成.

责任编辑 徐国坚