运用SOLO分类理论指导教学设计,有效提升学生思维发展水平
2022-05-30莫与谈
莫与谈

[摘 要] SOLO分类理论作为评价学生思维结构水平的理论,将之应用到小学数学课堂教学设计及课堂教学活动,不仅具有可行性,还能准确地把握学生的思维结构层次,促进学生思维水平的发展。
[关键词] SOLO分类理论;教学设计;思维
SOLO分类理论是一种评价学生思维结构水平的理论,主要应用于试题的编制及教学目标的制定,在学生学习结果的评价方面得到了广泛的应用,且取得了良好的效果。SOLO分类评价理论的核心是学生的思维结构水平,依据学生的学习结果将学生的思维水平划分为五种结构层次,分别是前结构层次、单一结构层次、多点结构层次、关联结构层次、拓展抽象结构层次。近年来的研究表明:SOLO分类理论应用于教学设计不仅可行,而且为教学设计提供了科学的理论指导。笔者在这一理论的指导下,以“比的意义”教学设计为例,期望为学生的认知经历和思维水平的发展带来更多启发。
[?]一、充分做好前侧,了解学生思维水平
“比的意义”是人教版六年级上册第四单元第一课时的内容,学生学习这一知识前已经掌握了除法的意义与商不变的性质、分数的意义与基本性质、分数与除法的关系等知识。为了解学生对比的认知情况,笔者在课前开展了前测。前测发现:部分学生不明白比表示的意思,认为比是表示两个数之间的一种数量关系。为进一步弄清学生的真实想法,笔者对这部分学生进行了访谈。他们认为,比就是相当于把比号前后的两个数字进行比较,有大小关系、相减关系、和的关系和倍数关系等不同的说法,对于比与生活中球赛比分的区别辨析不清。极少数学生知道比和除法、分数、百分数、小数之间存在的联系,但说不出所以然来;少数学生从金龙鱼的广告中还知道比可以表示多个量之间的关系,但没有关注具体可以表示几个量之间的关系。
[?]二、结合课程标准,精心完善教学设计
1. 基于理论定目标,把握思维层
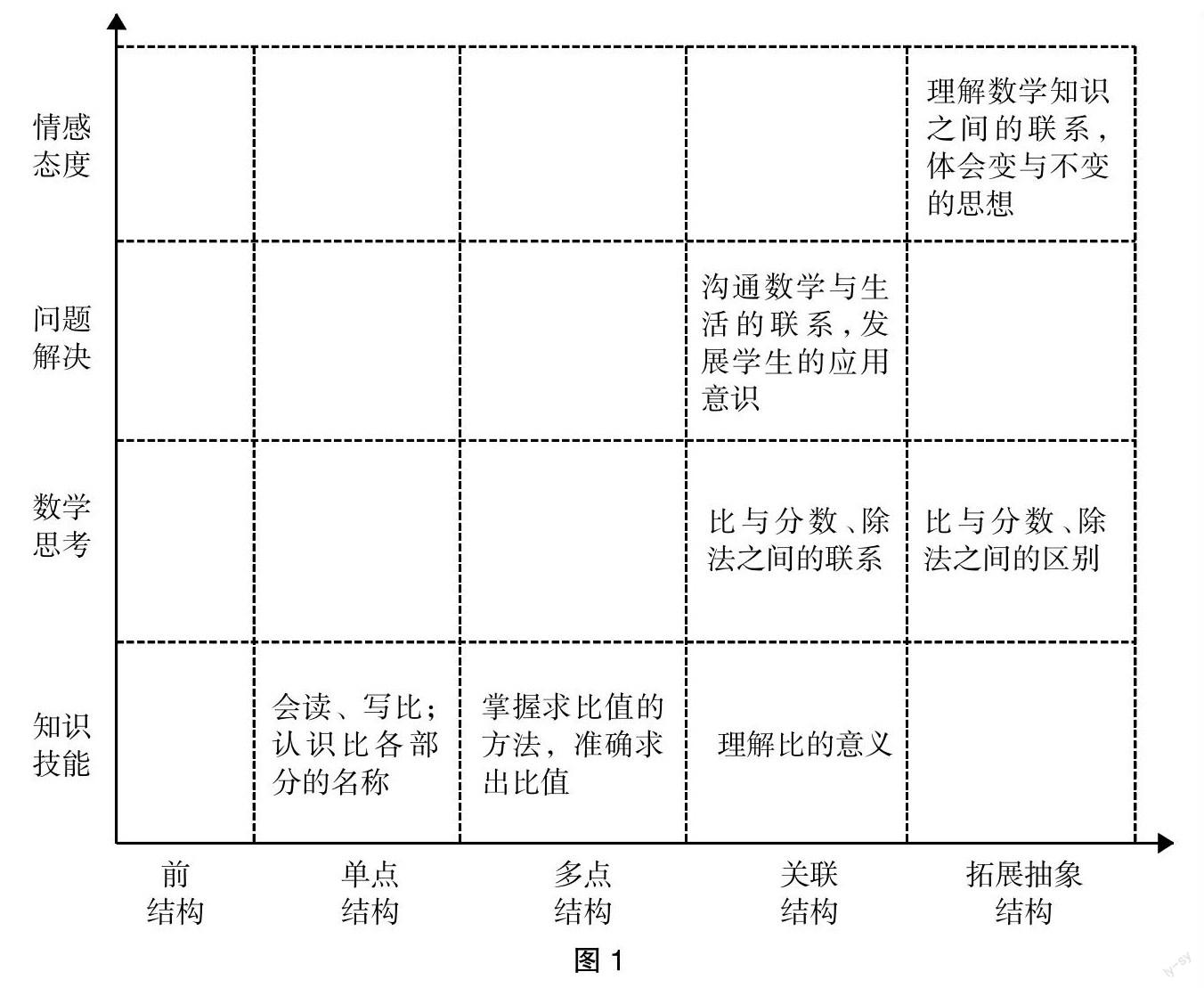
笔者依据SOLO分类理论的思维层次,确定了本节课的教学目标(如图1)。
2. 基于理论定重难点,抓住思维层
在目标的引领下,本节课的教学重点定为:理解比的意义,这是关联结构的思维水平;教学难点定为:理解比与分数、除法之间的关系,这也是关联结构的思维水平或从关联结构向拓展抽象结构发展。
3. 基于理论定设计,发展思维层
(1)感悟“比”
创设情境(出示课外实践学做包子的图片):校外实践课上,小明、冬子、小刚三位同学学做包子,指导老师告诉他们,做包子前先要学会和面,面粉和水的比是2∶1。听了老师的介绍后三人立即开始行动。
教师出示学生的作品(如图2所示):
讨论:你们认为几号作品是成功的,对于失败的作品,原因可能是什么?
生1:3号作品是成功的。
生2:2号作品水放多了。(课件出示正确的做法:2碗面粉1碗水)
生3:3号作品应该是水放少了。
生4: 3号作品也可能是装面粉的碗大,装水的碗小,导致水少了。
师:也就是说面粉和水的比是2∶1,前提是装面粉和装水的碗一样大。
鉴于前测发现,多数学生对比的认知较少,即无法理解比所表示的意义,或答非所问。根据SOLO分类理论分析,发现多数学生对比的认知处于前结构水平。因此在这一环节的设计中,让学生根据生活经验初步感悟2:1在具体情境中的意义,同时教师也可以根据学生的回答,及时分析学生的情况,及时调整提问的深度。
(2)认识同类量的“比”
师:面粉的量和水的量的比是2比1,记作2∶1。也可以说,水的量和面粉的量的比是1比2,记作1∶2。这里的2∶1和1∶2表示的意思一样吗?(理解前后项交换后表示的意义不同)
生(齐):我们认为这里的2∶1和1∶2表示的意思不同,2∶1是面粉和水的比,表示2份面粉和1份水;1∶2表示的是水和面粉的比,表示的是1份水和2份面粉。
和面游戏:教师说面粉的量,学生说水的量;教师说水的量,学生说面粉的量。教师及时将数据记录在黑板上。
师(指出数据):面粉和水之间究竟存在着什么关系?
生5:面粉是水的2倍。
生6:倍數关系。
生7:几分之几的关系。
师追问:如何求一个数是另一个数的几倍或几分之几呢?
生8:用除法。
生9:我明白了,它们之间还存在着相除的关系。(其他学生表示同意)
SOLO分类理论中的单点结构意味着学生在学习过程中能集中精力关注到问题的一个方面。此环节中教师借助日常生活中学生熟悉的生活情境,让学生充分理解2∶1的意义,即“比”中同类量的比,同时理解同类量的比中两个量之间存在的关系。
(3)认识不同类量的“比”
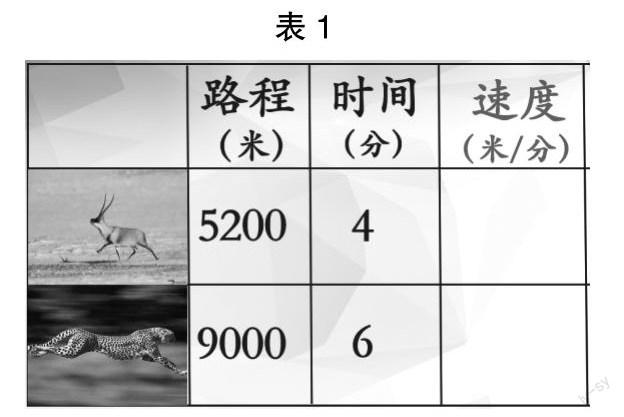
(出示藏羚羊和猎豹的图片)比较谁跑得快,完成表1。
师:你是怎么列式求它们的速度的?
学生列式,教师板书:5200÷4,9000÷6。
师:你能分别写出路程与时间的比吗?
学生口答,教师板书:5200∶4,9000∶6。
师直接指出:路程与时间的比得到的是一个新的量——速度。
师:其实类似这样的关系在生活中还有很多(出示问题,在师生互动和生生互动中解答)。
明明用2.4元买了6册练习本。请你写出花的钱与练习本数量的比。你知道这个比实际上表示的是什么吗?
师:现在谁能归纳一下,两数的比表示的是什么意思?(两个数的比表示两个数相除)
这一环节是本课中学生的思维由多点结构向关联结构发展的开始。设计中通过学生熟悉的速度、路程和时间三者的关系,先让学生轻松地根据已知条件分别列式求出两种动物的速度,然后写出路程与时间的比。此时,教师直接指出:路程与时间的比得到的是一个新的量,即速度。由于有了前面的铺垫,学生容易理解5200÷4与5200∶4之间的关系,促使学生将这里不同类量的“比”与之前同类量的“比”联系起来。接着,教师通过熟悉的单价、总价和数量之间关系的巩固练习,引导学生得到比的意义:两个数的比表示两个数相除。这一设计发展了学生的思维,有助于学生形成有层次的知识体系。
(4)自学“比”
出示自学提纲,学生自学课本第49页的内容,同桌交流,全班反馈,在反馈中掌握比的读写法、比各部分的名称、求比值的方法及比的不同呈现形式。
SOLO分类理论中的单点结构,只需要学生关注到其中的单个信息即可。读、写比,认识比各部分的名称及求比值的方法等在单点思维水平的层次上学生可以自学完成——通过交流、反馈掌握这些知识。
(5)探究“比”
小组合作:探究比和除法、分数三者之间的关系。课件出示比与除法、分数三者之间的联系和区别的表格,小组讨论,全班交流。
师:你在生活中见过这样的“比”吗?(出示意大利队与韩国队足球比赛的图片,显示比分2∶0)这里的2∶0是什么意思?与我们今天所学的“比”的意义一样吗?
生(齐):意义不同,我们今天学习的比表示的是两个数的相除关系。这里的2∶0的后面是0,我们所学的“比”后项不可以为0,它们只表示两个队进球多少的关系。
本环节让学生将所学知识与相关联的旧知联系起来,理清它们之间的联系与区别,培养学生分析问题、归纳问题的能力以及语言表达能力,以期学生的思维达到SOLO分类理论中的关联结构水平(或接近拓展抽象结构水平)。
(6)深化“比”
(出示吹泡泡图)呈现泡泡水的制作方法,甘油、水、洗手液和洗洁精的比是1∶4∶2∶2,引导学生体会“比”较于除法、分数的优越性。
师:你能用自己的话说说1∶4∶2∶2的意思吗?
此设计旨在让学生体会到除法和分数只能表示两个量之间的关系,而比不仅可以表示两个量之间的关系,还可以表示多个量之间的关系,这正是比的优越性所在。
(7)深挖“比”
师:这节课我们一起学习了比的哪些知识?你有什么收获?
借助思维导图及文字叙述,列出本节课的知识。
[?]三、借助科学理论指导,有效提升思维水平
通过全课的学习,学生全面掌握并充分理解了比的意义,为今后进一步学习比的其他知识、圆周率、百分数、统计及比例等奠定了良好的基础。此外,比的知识也进一步发展了学生对除法和分数的认识,进一步沟通了知识之间的联系,提升了学生运用知识和解决问题的能力。可以看到,在本节课的小结阶段,教师借助思维导图及学生的回答叙述,让全体学生形成了本课的知识网络结构图,使得众多学生的思维水平由多点结构向关联结构发展,实现了本节课让学生的认知经历和思维水平得到相应发展的预设目标。
SOLO分类理论作为评价学生思维结构水平的理论,为课堂教学设计提供了科学的理论指导,使教师能科学设计教学目标,合理安排教学过程,恰当选择教学方法,准确把握学生的思维层次。本节课的教学实践也证明,以SOLO分类理论指导小学数学课堂教学设计及课堂教学活动具有可行性,能促进学生思维水平的发展。
