基于学习路径分析的“两位数乘两位数”单元整体教学
2022-05-30杨国雄章勤琼邓建文
杨国雄 章勤琼 邓建文

【摘 要】运算能力的两个重要内涵是理解算理和掌握算法,计算教学中需要促进算理与算法的融合。“两位数乘两位数”是学习多位数乘法的关键单元,教学重点是两位数乘两位数算理的理解以及算法的掌握。教师依据基于学习路径分析的单元整体教学框架,对教材原有的编排形势进行了调整,思考单元教学路径,设计了笔算连续课,以算理理解的水平层次促进算理的深度理解,注重竖式记录的关联性,更好促进“法理融合”,提升运算能力。
【关键词】学习路径;单元整体教学;运算能力;法理融合
运算教学是小学数学教学中的主要内容,它贯穿小学数学学习的每一个阶段。运算能力是学生最重要的核心素养主要表现之一。《义务教育数学课程标准(2022年版)》中指出:“运算能力主要是指根据法则和运算律进行正确运算的能力。”[1]因此,教师在“数的运算”教学中,不仅要关注学生运算技能的掌握,更要注重学生对算理的理解,从而发展学生的运算能力。而且,与之前相比,增加了“能够明晰运算的对象和意义,理解算法与算理之间的关系”[2]。因此,促进算理与算法融合,需要教师对计算教学引起更多的重视。
“两位数乘两位数”单元是整数乘法主题序列学习的重要组成部分,也是学生真正开始学习多位数乘法的核心内容。以人教版教材为例,学生已经学习过“表内乘法”和“多位数乘一位数乘法”,具备了较好的乘法学习基础。进入“两位数乘两位数”单元,学生要继续学习相关的口算乘法、两位数乘两位数笔算乘法、运用两步计算解决问题。其中两位数乘两位数笔算是运算教学的重点和难点。因此本单元的教学要侧重于算理、算法的探索并促进算理、算法的融通,使学生在明理中掌握计算方法。基于学习路径分析的研究框架[3],教师可以对“两位数乘两位数”单元进行整体教学的思考。
一、理解单元学习目标
(一)单元内容概述
人教版教材四年级上册“两位数乘两位数”单元的学习目标主要包括:掌握两位数、几百几十数乘一位数(进位),两位数乘整十数、整百数(不进位),整十数乘几百几十数(不进位)的口算方法;经历两位数乘两位数的计算过程、理解算理,掌握两位数乘两位数的计算方法;经历问题解决的过程,学会用两步计算和不同的方法来解决问题。
北师大版教材四年级上册“乘法”单元的学习目标主要包括:结合具体情境,探索两位数乘整十数、两位数乘两位数的计算方法,经历交流算法的过程,理解算理;掌握两位数乘两位数的计算方法,解决简单的实际问题。
对比发现,两种版本的教材关于“两位数乘两位数”单元的学习目标有所不同,但都含有三个方面的内容:一是掌握两位数乘整十数的口算方法;二是经历探索两位数乘两位数的计算过程、理解算理,掌握两位数乘两位数的计算方法;三是解决实际问题。
(二)确定核心目标
本单元属于“数与代数”领域中“数与运算”主题的教学内容,应重点关注学生运算能力的培养。算理与算法是运算教学中的两个关键要素,二者是相互联系、有机统一的整体,能较好地理解算理和掌握算法是学生具备运算能力的主要表现。[4]
“两位数乘两位数”是整数笔算乘法学习的跨越阶段,学生第一次接触分两层记录的乘法,理解难度较大。一方面,学生要理解乘的顺序,明白分层记录的原理;另一方面,学生要理解各部分积的书写位置。因此,教师在本单元的教学中要重点关注两位数乘两位数的算理理解和竖式记录两个方面,做到算理、算法并重,以算理理解促进算法掌握。所以本单元的核心目标是探索并理解两位数乘两位数的算理,掌握两位数乘两位数的竖式记录方法。
(三)核心目标具体化
结合以上整体分析,将核心目标具体化为两点。一是理解两位数乘两位数的算理。其主要内涵包含四个水平层次:能理解两位数的结构以及乘法算式的意义;能有自己的计算方法并说明理由;能理解不同的方法,并且能够比较不同的方法;能在表征、比较的基础上提炼通法。二是掌握两位数乘两位数竖式记录方法。具体表现为学生能感受情境意义、计算过程与竖式记录的关联,理解竖式中每一步的意思,建立算法模型。
二、确定学习起点
为了解学生对核心目标的理解水平,笔者从两位数乘两位数的算理理解和竖式记录两个方面对一个日常教学班开展学情调查。
(一)学生的算理理解水平分析
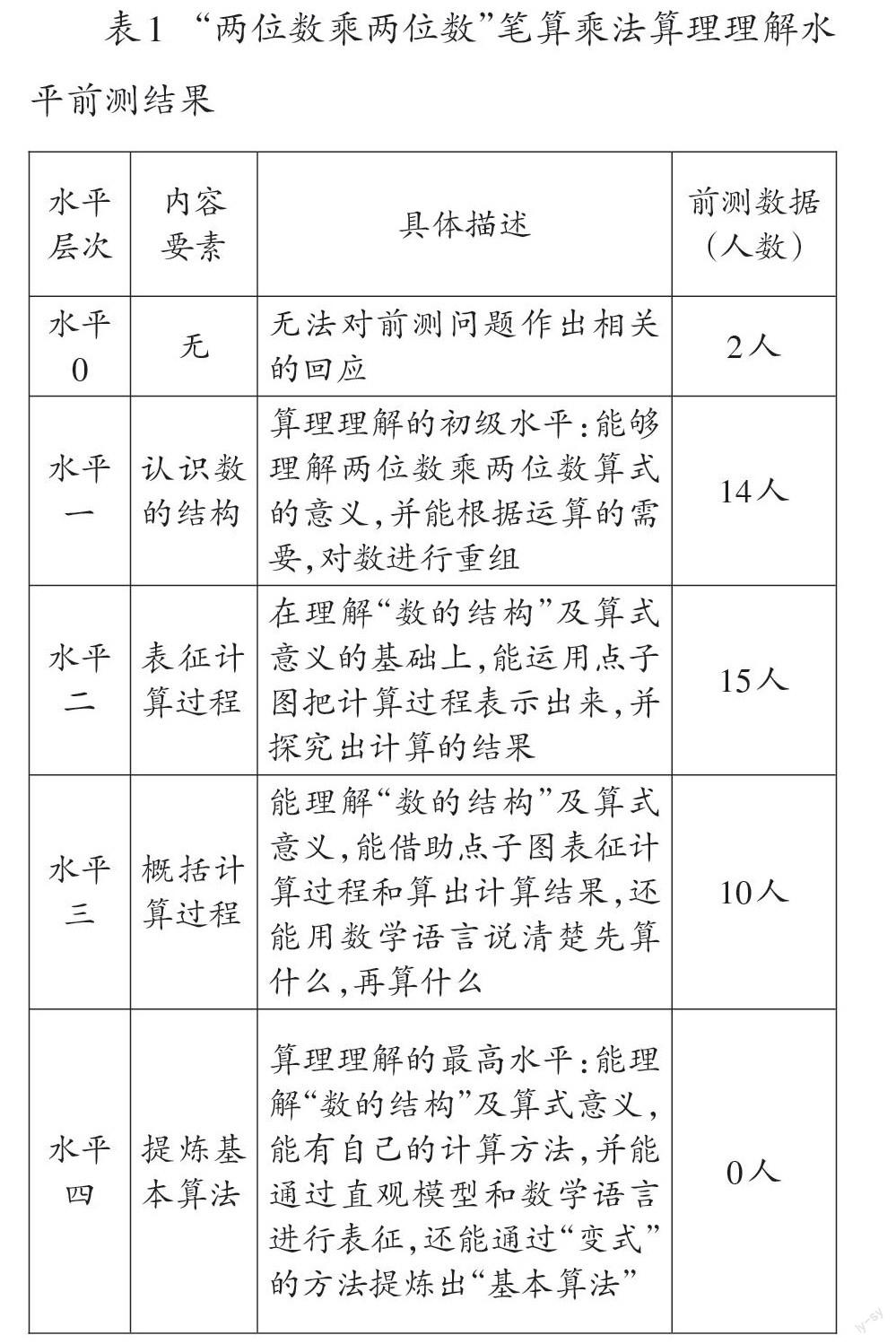
为真实了解学生算理理解水平,以算理理解的四个水平层次为基础[5],建构两位数乘两位数笔算算理理解表现性评价框架,笔者开展了前测,前测题如图1所示。
测试题:想一想“13×12”的意义是什么?怎么计算?请你用横式写一写你的计算方法,并试着用点子图把你的方法表示出来。
从前测结果可以发现,大部分的学生能够理解乘法算式的意义,能对数进行重組,超过一半的学生能够画分点子图和用自己的方法找到13×12的计算结果,但很大部分学生无法准确地用数学语言表达操作过程,无法说清楚“先算什么再算什么”,不能从“非基本算法”中自发地进行优化,提炼出“基本算法”。
(二)学生的竖式记录情况分析
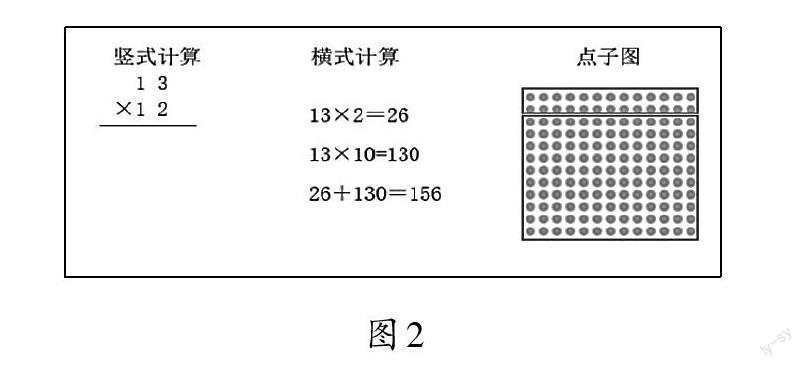
为真实了解学生竖式记录情况,笔者同样开展前测。前测题如图2所示。
学生解答方法与情况统计如下。
根据前测数据可以发现,有5+3+4+7=19名学生无法写出正确的乘法竖式,且竖式记录存在难度。此外,笔者对写出正确竖式的14+8=22名同学进行了进一步的访谈,了解他们能否将竖式、横式、点子图进行关联,理解乘法竖式每一步的意思。访谈结果显示,22名同学中有6人无法将竖式、横式、点子图进行一一对应,他们只是通过识记、模仿的方式进行竖式记录。因此,教师有必要让学生经历从横式到竖式的形成过程,沟通横式、竖式和图式之间的联系,做到算理、算法融通,帮助学生建构算法模型。
三、单元整体设计的思考
按照人教版教材的编排,“两位数乘两位数”单元的学习分为三个阶段:第一阶段学习相关的口算乘法内容;第二阶段学习两位数乘两位数的笔算,先学习不进位的笔算,再学习进位的笔算;第三阶段学习运用连乘、连除两步计算解决问题。
根据学情分析,学生对“两位数乘两位数”笔算的算理理解、竖式记录存在不同程度的困难。因此在笔算教学中,教师应该依据算理理解的水平层次促进学生对算理的深度理解,同时做好情境意义、计算过程和竖式记录的关联,实现算法模型的意义建构。
综上分析,笔者对“两位数乘两位数”的单元教学内容作以下调整。
1.删除口算乘法例2中“6×10”作为新知的教学。因为学生已经完全掌握了“6个十就是60”的口算方法,而教材生硬地向学生介绍6×9再添加一个6这样的算法,虽然有情境的支撑,但不符合学生的认知结构,甚至会扰乱学生的已有认知。教师可以将6×10放在复习引入环节,让学生在口算练习中复习算法,体会口算一位数乘10方法的简便性,改用“12×10”作为探索两位数乘整十数的例题进行教学。
2.将“两位数乘两位数笔算”作为探索多位数乘法算理和算法的关键课。算理的理解直接关系到算法的掌握,所以在教学中要强化算理理解的教学。教师可以将两位数乘两位数笔算设计成笔算连续课,所谓笔算连续课就是用连续的2个课时进行教学,其中课时1指向算理的理解,课时2指向竖式的教学。笔算连续课的设计可以打破教材原来按照“不进位”“进位”根据内容来编排的方式,而改为从理解算理、做好“竖式记录”的角度进行教学。这能够有效促进学生对算理的理解和算法的建构,在算理、算法的融通上给予学生更多的时间和空间,同时连续课的形式保证学生思维的连贯性与整体性。
基于以上的整体思考,教师可对“两位数乘两位数”单元的教学的“序”做以下调整(如表2),构建符合学生认知规律的学习路径。
通过上表可以发现,调整后的单元教学内容仍然分为口算乘法、笔算乘法、解决问题三个阶段,其中笔算乘法作为本单元的核心内容,进行了较大的教学调整。教师将原来教材安排的不进位与进位的两位数乘两位数笔算乘法设计成笔算连续课,用连续的两个课时进行教学,第一课时依据算理理解水平层次做好算理理解教学,不进入竖式教学,第二课时让学生经历竖式的形成过程,做好竖式、横式与情境的关联,帮助学生理解两层竖式的合理性,建构算法模型。本单元具体教学内容的安排如表3所示。
参考文献:
[1][2]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
[3]章勤琼,陈锡成.基于学习路径分析的小学数学单元整体教学思考框架[J].小學教学(数学版),2021(3):13-16.
[4]章勤琼,杜依铭.运算教学中如何做到“法理兼顾”:略谈运算教学的三个要点[J].福建教育,2022(10):28-31.
[5]章勤琼,阳海林,陈肖颖.小学数学教学中的表现性评价及其应用[J].课程·教材·教法,2021(3):83-89.
(1.广东省东莞市松山湖第二小学 523429
2.福建师范大学教育学院 350117)
