横向拓宽求联 纵向深入追理

【摘   要】从两位数乘两位数入手，探究“乘积最大的秘密”，并将学习的方法、发现的规律迁移到对三位数乘两位数、多位数乘多位数的研究中。通过从两位数到多位数的延伸探究推进学生思维纵深发展;通过从算式到图形的方法关联拓宽学生思维广度;通过从特殊到一般的迁移类推促进学生思维灵活。学生在发现乘积最大秘密的过程中，可通透知识内容的本质，提升解决问题的能力。

【關键词】横向发散;纵向深入;关联

思维的条理性源于知识的结构化。教学中，教师应以数学核心知识为统领，或引导学生的思维由聚到散地横向扩展，使其对知识的理解、对方法的掌握，更加全面;或引导学生的思维由浅入深地纵向深入，将核心知识沿着问题的线索研究通透。通过横向扩展、纵向深入，学生的思维变得广阔、深刻、灵活，由此及彼地扩大知识的外延，突破原有的认知结构，构建新的认知结构。

基于“一题一课”的“乘积最大的秘密”教学，从两位数乘两位数入手，展开探究，再进一步将思考拓展至三位数乘两位数、多位数乘多位数，让学生发现并理解“乘积最大的秘密”，培养学生数形结合、模型思想，发展想象和推理能力，促进对乘法意义的进一步理解。本节课既是对长方形面积与周长关系的抽象概括，又是对乘法分配律的提前渗透。

【教学过程】

一、前设求联：整体建构，探索两位数乘两位数

出示问题：用1、2、3、4这四个数字组成两位数乘两位数的乘法算式（每个数字只能用一次），怎样组乘积最大？

1.理一理，聚焦关键算式

生：43×21。

生：41×32。

生：42×31。

……

（板书算式）

师：上面这些算式，哪些可以直接排除？

生：我觉得43×21可以直接排除，用估算的方法，把43估成40，把21估成20，它们的积只有800多，而其他两个算式的积应该有1200多。

生：题目要求的是乘积最大，所以必须把4和3放在十位上，才能保证乘积最大。

师：看来要使乘积最大，首先我们得确定高位。

（板书：先确定高位）

师：该怎么确定高位？

生：把较大的4和3分别放在两个数的高位上。接着，在个位上填入剩下的1和2，得到了41×32和42×31这样两个算式。

（设计意图：创设情境，提出寻找乘积最大秘密的问题，激发学生探究的兴趣。出示题后，学生写算式，通过估算排除积一定不是最大的算式，留下41×32和42×31两个算式。以上过程有效激活学生原有的口算、估算、笔算等知识经验，为后续找乘积最大的秘密做好铺垫。）

2.算一算，比较积的大小

师：同学们很会动脑筋！那么41×32和42×31到底谁的积更大？还能通过估算得到吗？请根据活动要求完成任务。

任务一：四人小组合作，探究41×32和42×31谁的积更大，并把小组内讨论的方法记录下来。

活动要求：

算一算：选择你喜欢的方法求出哪个算式的积更大。

想一想：你可以怎样解释为什么这个算式的积更大？

说一说：把你的想法说给小组成员听。

（1）就数论数。

生：我利用列竖式的方法求得两个算式的积分别是41×32=1312，42×31=1302，从而发现41×32的积更大。

生：我通过计算器直接计算并比较。

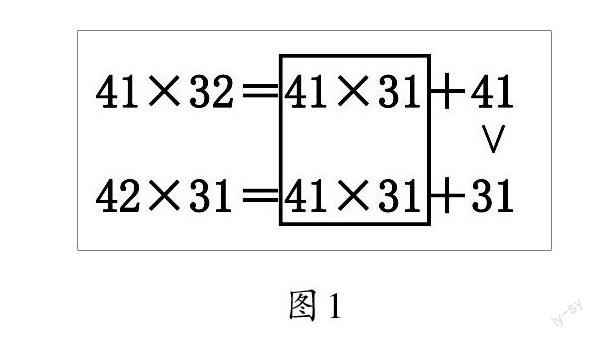
生：我把算式拆分了，41×32=41×31+41×1，42×31=41×31+1×31。可以看出第一个算式比41×31多了1个41，第二个算式比41×31多了1个31，41>31，所以第一个算式的积更大（如图1）。

（2）以形验数。

师：同学们用了不同的方法求得41×32的积最大。如果用一个图形表示41×32，你会用什么图形？（长方形）41是这个图形的什么？32呢？

生：41是它的长，32是它的宽。

师：我们用另一个不同颜色的长方形表示42×31，它的长和宽分别是多少？

生：它的长是42，宽是31。

师追问：想一想在图形中1312和1302表示什么。

生：1312和1302正好是这两个长方形的面积。

师：看来比较这两个算式乘积的大小，其实就是比它们面积的大小。请拿出信封里的两张长方形纸片比一比它们的大小。

生：可以利用画一画、折一折的方法来比较这两张长方形纸片的大小。

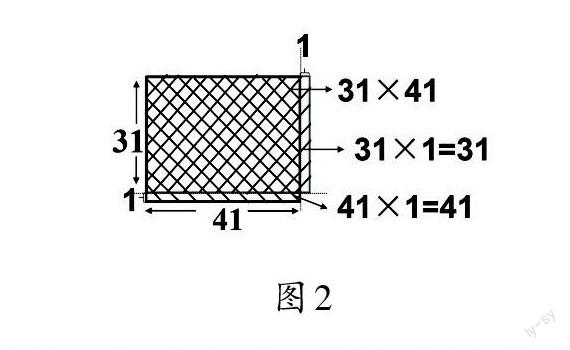
师：刚才有同学利用拆分算式的方法发现第一个算式多了1个41，第二个算式多了1个31，你能结合图2解释为什么会多1个41和1个31了吗？

生：通过折一折，也可以发现多出来的第一个长方形的面积是41×1，多出来的第二个长方形面积是31×1，第一个长方形面积比第二个长方形的面积多10，41×32的积正好比42×31多10。

师：长方形中，好像也隐藏着乘积最大的秘密。这节课我们就来研究乘积最大的秘密。

（教师出示课题）

3.练一练，建立算式模型

出示练习：用9、8、7、6四个数字组成□□×□□的算式，哪个算式乘积最大？

师：你能不计算直接写出乘积最大的算式吗？

生：能。可以先确定高位一定是较大的9和8，得到96×87和97×86两个算式。

生：96×87=96×86+96，97×86=96×86+86，96>86，所以，96×87的积更大。

师：同学们仔细观察41×32、96×87这两道乘积最大的算式，它们的数字排列有什么共同特点？

生：我发现这些数都是最大的数和最小的数组成一个两位数，排在中间的两个数再组成另一个两位数。

师：你们真会观察，如果用ABCD表示从小到大的4个数字，组成□□×□□的算式，怎样安排乘积最大？（如图3）

生：DA×CB。

师：为什么这样乘积最大呢？

生：因为长方形的长和宽越接近，面积越大，这样排列后，BC与DA的差更小，所以得到的积更大。

（设计意图：从直接计算到算式拆分，从“就数论数”到“以形验数”，将乘法与长方形面积相结合，沟通乘法算式与长方形面积之间的关系，让抽象的算式变得直观，有利于学生对于乘积最大原理的深度理解。得出规律后，再一次聚焦乘积最大算式的数字排列特点，用字母的形式表示积最大的模型，将两位数乘两位数乘积最大的这类问题一般化，沟通乘积最大问题的联系，构建解决问题的数学模型。）

二、中间求变：适度开放，探究三位数乘两位数

师：如果再增加一个数字，写出三位数乘两位数的算式，怎样写乘积最大？

1.有“0”时三位数乘两位数积最大的情况

出示问题：用0、1、2、3、4这五个数字组成一个三位数乘两位数的乘法算式（每个数字只能用一次），使得积最大。

生：先确定高位是4和3，最小的0一定在末尾，当末尾有0时可以先不看0，因此我们可以把0先藏起来。

生：将问题转变成了4个数字写乘积最大的算式，就可以利用AD×BC模型得到41×32。最后把0添在末尾，有两种情况：410×32=13120或41×320=13120。

2.无“0”时三位数乘两位数积最大的情况

师：请根据活动要求完成任务二。

任务二：用1、2、3、4、5这五个数字组成一个三位数乘二位数的乘法算式（每个数字只能用一次），使得积最大。

活动要求：

（1）猜一猜：怎样的算式乘积最大？

（2）验一验：列一列算式，验证自己的猜想是否正确。

（3）理一理：理清自己的想法，准备汇报。

生：先确定高位分别是5和4，把3放在4的后面，把2放在5的后面，最后确定1的位置。

师：为什么不是53×42呢？

生：53×42=52×42+42，52×43=52×42+52，52>42，所以要把3放在4的后面。

师：最后的“1”，应该放在哪里呢？

生：因为把“1”放在43的后面，所得的积比520×43的结果多了一个52，把1放在52的后面，所得的积比520×43的结果多了一个43，所以“1”放在43的后面。52×431的积是最大的。

（课件动态演示，如图4）

师：你也能像刚才那样，用几个字母来归纳三位数乘两位数乘积最大的模型吗？

生：用ABCDE表示从小到大的5个数字，那么三位数乘两位数乘积最大是EB×DCA。

（设计意图：在解决了两位数乘两位数积最大问题后，继续引导学生探究三位数乘两位数积最大的秘密。三位数乘两位数有两种情况，一种是其中一个数字是“0”，另一种是没有“0”，让学生的思维由浅入深，通过迁移类推，关联分析，发现三位数乘两位数的积最大的原理。最后，再一次构建解决问题的数学模型，使数学建模成为学生思考与解决问题的一种方法，在探究中寻找积最大的秘密。）

三、后置求用：实践体悟，拓展多位数乘多位数

师：如果继续增加数字，乘积最大又是多少呢？

出示问题：用0～9这九个数字组成一个乘法算式（每个数字只能用一次），使得积最大。

生：先确定高位分别是9和8，7放在8的后面，6放在9的后面。

生：为什么6要放在9的后面，7放在8的后面呢？

生：97×86=96×86+86，96×87=96×86+96，96>86，所以要把6放在9的后面。

生：按照这样的排列，可列出算式：9642×87531，“0”放在哪个数的后面都是一样大，所以9642×875310和96420×87531乘积最大。

（设计意图：多位数乘多位数，促使学生的思维水平从“关联结构”跃至“抽象拓展”。整个探索过程用“ɑ×b等于ɑ个b相加”来解释数字放置的原因，不仅让学生再一次理解乘法的意义，还帮助学生学生透析了乘积最大的秘密，掌握解决问题的方法，并应用此方法解决同种类型、更深层次的问题。）

【教学思考】

学生在多位数乘积最大问题的学习中，步步深入，充分理解基本原理，并在此基础上进行方法探究。

一、由浅入深，从“两位数”到“多位数”的蔓延

从两位数乘两位数积最大的基本问题入手，让学生初步感知要想让组成的算式积最大，就要将较大的数先固定在高位。再探究添加一个0时，为了让三位数乘两位数的积最大，要将0先藏起来，转化成两位数乘两位数积最大的模型。最后将0变成1，探究三位数乘两位数积最大的模型即可，通过迁移类推，乘积最大问题迎刃而解。整个学习过程，教师利用层层推进的问题，帮助学生看透知识内容的本质，推动思维的纵深发展。

二、由聚到散，从“就数论数”到“数形结合”的转变

“数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事休。”将算式乘积的大小比较转化成长方形面积的大小比较，沟通算式与图形的联系，方法与方法的联系，可助力学生亲身经历、体验“数形结合”的过程。有了几何直观的支撑，学生能更好地掌握乘积最大问题的内在意义。这也是形象思维与抽象思维协同运用、互相促进、共同发展的过程。这样的过程有助于培养学生的数形结合思想，开拓学生的视野，提高学生思维的灵活性。

三、由此及彼，从“特殊算式”到“一般算式”的迁移

探究“乘积最大的秘密”本身就是模型建立的过程，学生通过计算、观察、猜想、验证等活动，初步建立这一类题的探究模型。在探究“两位数乘两位数什么时候乘积最大”后，自然地引出用ABCD表示从大到小的四个数字，建立积最大的模型为DA×CB，把两位数乘两位数乘积最大的這类问题一般化，沟通乘积最大问题的联系，构建解决问题的数学模型。教师有意识地渗透模型思想，让学生从直观中感受抽象概括，洞悉数学知识间的逻辑关系，让思维走向通透。

参考文献：

[1]郑毓信.数学应当让学生学会思维（上）：数学核心素养的理论性思考与实践性解读[J].湖南教育·C版，2017（1）.

[2]鲍善军，朱曙光.基于SOLO分类理论的“一题一课”教学设计与实践[J].教学月刊·小学版（数学），2021（11）.

[3]朱曙光，鲍善军.从“方”到“圆”以“点”带“面”：《怎么围面积大》教学实录与评析[J].小学教学设计（数学），2021（5）.

（浙江省杭州市钱塘区临江新城实验学校   310018）