以题促思，提升教师专业研究能力的路径

戴伟清

[摘  要] 教师的专业发展源于内驱，在教学过程中，教师经常会在一瞬间产生灵感，如果把这些灵感记录下来并加以整理，那么必将对教师的专业发展起到推动作用. 在解题过程中，教师有时会经历一些挫折和失败，但是在失败中也会有颇多收获，所以研究解题能促进教师进行专业思考，是提升教师专业研究能力的有效路径之一.

[关键词] 解题;反思;提升;专业研究

教师的专业成长源于教师自身的需求，一线教师受多方压力，对教学研究往往很难迈出步伐. 数学教师在教学过程中，有超过一半的备课时间用于数学解题，因为解题能力是衡量数学教师教学能力的一项重要指标. 在解题的过程中，教师会产生很多的教学想法，有时候一些想法一闪而过，有时候一个问题会纠结几天，但最终会被遗忘. 如果教师能够在灵光闪现的时刻，把自己的想法写下来，或记录解题方法、过程，或记录解题感悟，长期坚持，当教师回顾自己的这些过程时，其实就是一个自身专业成长的过程.

数学课程标准中提出：建立数感、符号意识和空间观念，初步形成几何直观和运算能力，发展形象思维和抽象思维. 几何直观是图形在已有条件下反映出的最本质的特性，包括角度、边的长度、面积大小等方面，人们通过直观感受，能确定几何图形特定的位置. 几何直观在数学学習中的重要地位正如著名数学家弗赖登塔尔所说：几何直观可以告诉我们什么是重要的、有趣的和容易进入的，当我们陷入问题、观念、方法的困扰时，几何直观可以引领我们从最本质的问题中去寻求解决方法. 在初中数学教学过程中，教师应努力感受几何直观带给自身对几何图形的感知，从中发现几何图形的内在特征，并借助数学的其他方法解决问题.

问题的提出

在一天中午的自习课上，笔者所在班级的一名学生拿着一道题来问笔者.

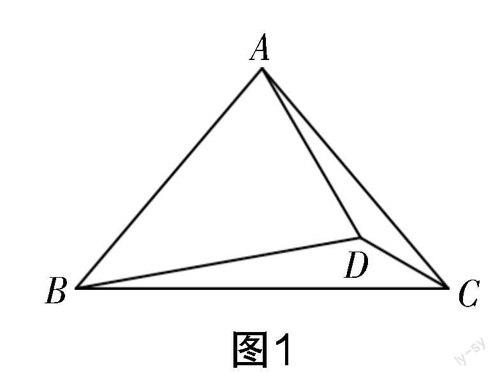
原题如下：如图1所示，在△ABC中，AB=AC，∠ABC=50°，在△ABC内部有一点D，且∠ABD=40°，∠ACD=20°，求∠BAD的度数.

当笔者看到这道题时，感觉它并不难，甚至应该很简单，因为这个三角形的形状和角度都是确定的，且点D在△ABC内部也是一个确定的点，本着定图定点的思路，这个角度必定可以求出来.

解决方法尝试

尝试策略1分析图形后可以得出∠ABC=∠ACB=50°，∠ABD=40°，∠DBC=10°，∠BCD=30°，∠ACD=20°. 要求∠BAD的度数，可以假设∠BAD=x，根据三角形的内角和可以得到∠ADB=140°-x，∠DAC=80°-x，∠BDC=140°. 那么∠ADC=80°+x. 点D处有一个周角，于是有140°-x+140°+80°+x=360°，然而这是一个恒等式，x无法求出. 难道这个x是不确定的吗？再次审视图形，发现BD是一条确定的射线，CD也是一条确定的射线，两条射线的夹角必定也是一个确定的值，所以这个角度必定是确定的. 那为什么会得到一个恒等式呢？这说明上述策略行不通，只能另外寻找解题途径.

尝试策略2如图2所示，延长BD交AC于点F，延长CD交AB于点E，并把图中的角度标注为∠1～∠4. 于是我们可以得到方程组∠1+∠2=80°，

∠1+∠3=100°，

∠2+∠4=120°，

∠3+∠4=140°. 看着4个未知数、4个方程，似乎方程组可以求解，但是前3个方程变形后就可以得到最后一个方程，这就意味着这个方程组其实只有3个方程，却有4个未知数，属于不定方程，同样无法求解.

两次尝试均以失败告终，看来笔者小瞧这道题了. 从题目中的关系看，∠BAD似乎和三角形的边没有关系，而且两次尝试始终是围绕着角度进行的，都无功而返了，这说明我们始终在原地转圈，无法找到解决办法. 试题出现了AB=AC，这说明△ABC是等腰三角形，接下来笔者从构造等边三角形的思路去尝试新的解题策略.

尝试策略3如图3所示，以AC为一边构造等边三角形AEC，连接BE. 因为∠BCD=30°，∠ACD=20°，所以∠BCE=10°. 因为∠ABC=50°，∠ABD=40°，所以∠DBC=10°. 所以BD∥EC. 根据AE=AC=AB，可知B，E，C三点在以点A为圆心的圆上. 所以∠EBC=∠EAC=30°. 因为∠DCB=30°，所以BE∥DC. 所以四边形BDCE是平行四边形. 所以BD=EC，AB=AC=EC=BD. 所以∠BAD=70°.

由上面的解题策略，我们可以以BC为一边作等边三角形EBC，连接EA，如图4所示. 根据题中的角度关系，可证明△ABE≌△ACE≌△DBC，所以AB=BD. 所以∠BAD=70°. 我们还可以以AB为一边作等边三角形ABE，连接DE，EC，如图5所示. 因为AB=AE=AC，所以B，E，C三点在以点A为圆心的圆上. 由圆周角定理可知∠BCE=30°. 由△BCD≌△BCE，得BE=BD. 所以AB=BD. 所以∠BAD=70°.

尝试策略4如图6所示，作∠BAC的平分线交CD的延长线于点E，连接BE，则∠BAE=∠CAE=40°，△ABE≌△ACE. 所以∠ABE=∠ACE=20°. 所以∠DBE=20°. 因为∠BDE=∠DBC+∠DCB=10°+30°=40°，所以∠BAE=∠BDE. 所以△ABE≌△DBE. 所以AB=BD. 所以∠BAD=70°.

方法反思这一构造角平分线的解法，显然比之前构造等边三角形的解法简单. 那么，这一解法是怎么想出来的呢？我们回到图形中角和边的关系. 题目出现了等腰三角形（即AB=AC），那么由这一条件我们可以联想到什么呢？对于等腰三角形，“三线合一”是非常重要的一种解题思路，于是我们尝试构造角平分线或者高或者底边上的中线. 对于此题，构造角平分线后我们得到了一些相等的角，还得到了一些全等的三角形，并顺利地解决了问题.

上面提供了此题的几种解法，从这些解法中我们发现，构造等边三角形的方法让我们得到了全等，构造角平分线的方法也让我们得到了全等，最终都是通过等腰三角形ABD来计算角度. 那么，能否更换这道题的角度呢？我们不妨做这样的假设：△ABC依然是底角为50°的等腰三角形，如果调整BD，CD与边BC的夹角，比如∠DBC=15°，∠DCB=25°，如图7所示. 从几何直观的角度我们可以感受到点D的位置是确定的，线段AD也是确定的，那么∠BAD的度数必然也是一个确定的值，那上述我们尝试的解法是否依然可行呢？实践后我们发现，构造等边三角形和角平分线的解法此时不适用了，无法解决问题. 所以构造等边三角形和角平分线的解法应该是特殊解法. 既然这个图是一个定图，所求角度也是一个确定的值，那么一定可解. 那我们还需要哪些解决问题的工具呢？从这个假设中我们可以预感到所求角度不是一个整数角度，所以我们需要用到三角函数.

我们依然从原题的数据中去深入研究，尝试利用三角函数来进行计算，期望可以得到和之前尝试策略相符合的数据.

尝试策略5我们尝试用正弦定理来表示边角关系. 由正弦定理可知，在任意一个三角形ABC中，===2R. 对于图1，在△ABC中，由正弦定理可得=，所以AB===. 在△BDC中，由正弦定理可得=，所以BD==. 所以AB=BD.

通过正弦定理我们发现，经过计算，问题依然转化到了边相等这个结论上，只不过运用了三角函数关系来进行转化. 此解法似乎也不是最一般的解决路径. 我们希望由三角形中明确的角度，来确定这个定点的位置. 经过一番思考和查询资料后，笔者找到了解决问题的一般方法. 这里需要用到角元塞瓦定理，这个定理的表述为：

如图8所示，在任意的△ABC中有一个内点P，则有··=1.

证明如下：在△APB中，由正弦定理得=，同理可得=，=. 三式相乘，得··=1.

对于原题，设∠BAD=α，则∠DAC=80°-α. 由上述定理，可得··=1，化解后可得sin70°·sin（80°-α）=sin10°·sinα，显然α=70°.

通过这个定理，我们就把确定角度的三角形内点问题的决定因素完全理清了. 不难发现，要解决此类问题，我们只需要知道这个内点分出的两个角度即可. 下面我们来看一道题（即下面的“问题”）.

问题如图9所示，在△ABC中，∠ABC=40°，∠ACB=40°，P为△ABC内一点，且∠PCB=∠PAB=20°，求∠PBC的度數.

解析设∠PBC=α，则∠PBA=40°-α. 容易求得∠PAC=80°，∠ACP=20°，根据角元塞瓦定理，得··=1，化简后得2sinα·sin10°=sin（40°-α），所以sinα·sin10°=sin（40°-α）=sin30°·sin（40°-α）. 观察可知α=30°，即∠PBC=30°.

变式如图10所示，在△ABC中，∠ABC=∠ACB=40°，I是△ABC的内心，连接IB，IC，在线段AB上取一点D，使BD=BI，连接DC，求∠DCI的度数.

解析因为∠ABC=∠ACB=40°，所以∠BAC=100°. 因为I是△ABC的内心，所以∠ABI=∠CBI=∠BCI=20°. 因为BI=BD，所以∠BDI=∠BID=80°. 设∠DCI=x，那么∠ACD=20°-x，∠BDC=120°-x，∠IDC=40°-x. 由角元塞瓦定理，得··=1，化简后得sinx=2sin10°·sin（40°-x），所以sinx=sin10°·sin（40°-x），即sin30°·sinx=sin10°·sin（40°-x）. 所以x=10°.

通过上述解决策略，我们终于弄明白了此类问题中的各种缘由，但在化简三角函数的过程中应用了二倍角公式，这超出了初中生的理解范畴. 应用角元塞瓦定理解题的过程中不难发现，有时得到的角度不是一个整数角度，因此此类问题看似明确有解，但实际求解时难度较大，且要恰好得到整数角度，题目中的已知条件就必须满足某些条件. 通过查询相关资料我们得知，如果三角形的三个内角都是10°的整数倍，三角形内一点同三个顶点的连线所分的角也是10°的整数倍，那么这样的问题通常称为“三角形角格点问题”. 角格点的数量是有限的. 当然，如果不是角格点，那就需要用计算器来求这个确定角的三角函数值了，此处不做详细说明.

教学反思

1. 教学切勿经验主义和教条主义

数学是一门抽象性、逻辑性较强的学科，教师在教学过程中遇到学生所提的问题，一定要审视问题的本质，切勿经验主义和教条主义. 笔者刚开始拿到此题的时候确实犯了经验主义的错误，认为图形确定就一定可解，认为通过角度的计算就可以得到答案，结果走入解题误区. 在平时的教学过程中，部分教师遇到自己做不出或者解答复杂的问题，有时就直接翻看答案，然后对照答案纠正自己的错误，还有部分教师甚至不知道为何会出错，或者不明白试题的解决思路源于何处，此时一旦有其他的切入点，他们也不能马上转变教学思路帮助学生解答. 所以教师必须自己分析试题并解答，且思考试题的本质，只有这样，才能遇问题不慌，遇困难不退.

2. 教学要有深入研究和探索的精神

我们经常要求学生做题要举一反三、触类旁通，其实学生提出的各种不同类型的问题，也能在某种程度上帮助教师进行专业研究，促进教师的专业成长. 譬如角元塞瓦定理，遇到上述试题之前，笔者不知道还有这一定理，但是在对问题进行深入研究的过程中，笔者为了寻找问题的关键，查阅了相关资料，知道了这一定理，并最终得到了解决问题的方法. 所以，在教学中，教师需要具备探索精神. 教学遇到困难时，教师不妨回到起点，回归数学最本质的问题，从基础出发，寻找思维的生长点，并从中不断推陈出新的题型，逐渐从注重解题技巧和解题方法转变为注重数学新思维的考量. 在教学过程中，教师应注重数学思维方式的渗透，要让学生用数学思维来看待生活问题.

3. 教学要坚持思考，不断自我革新

教师的专业成长道路非常艰辛，我们常常感觉时间不够. 题海战术已不适合目前的考试模式，且我们在教学过程中总会遇到新的问题，所以对于教学，我们需静心思考，潜心研究，并在教学的道路上不断自我革新，在不断探索与研究中促进自身专业能力的发展.

写在最后

“以小见大”是教学研究的出发点. 在教学过程中，我们会遇到无数的问题，这些问题都是我们的素材，只要我们做一个有心人，记录自己的教学思路，不断积累，就一定能让自己在专业研究的道路上越走越远，越走越好！