把握本质，精准施策

范韦莉

摘要：苏教版小学数学三年级上册“平移和旋转”的教学，要把握并立足平移和旋转的本质，精准选择教学方法，组织学习活动。数学本质的体会需要基于对相关现象的充分感知，可让学生进行多元表征以积累经验;需要遵循“先直观后抽象”的原则，可引导学生在比较归纳中探寻概念的本质;需要关注直观感受的获得，可组织学生自主操作，逐步丰富概念的内涵;需要重视学以致用，从而让学生感悟平移和旋转的价值。

关键词：数学本质;多元表征;比较归纳;自主操作;学以致用

一、教材解读和学情分析

（一）解读教材，明晰数学本质

平移和旋转都是物体或图形在空间变化其所在位置的运动方式，苏教版小学数学教材分两次教学有关的内容。第一次在三年级上册，主要是认识生活中的平移和旋转现象;第二次在四年级下册，主要教学在方格纸上平移、旋转较简单的图形。物体在现实空间的平移和旋转属于刚体运动学的概念，平面图形的平移和旋转属于图形变换的概念。在小学数学中，我们把前者称为“生活中的平移和旋转现象”，把后者看作对前者进行抽象的结果。

1.平移的本质

平移是指把图形（物体）从某个位置沿一定的方向直直地移动到另一个位置，得到的图形（物体）与原来的形状、大小完全相同，且其中的每一点都是由原图形（物体）中的某一对应点移动后得到，连接各组对应点的线段平行且相等。不难看出，平移的核心是“点”的运动，是自身包含的所有点在遵循平移条件下发生位移的图形变换过程。平移有方向、距离两个要素，运动方向可以是横向、竖向，还可以是斜向。三种方式中，横向平移和竖向平移最常见;斜向平移在小学阶段较为少见，且不少学生认为这不是平移，故教学时需要在这个地方引导学生思辨。

2.旋转的本质

旋转是指将图形（物体）围绕一个固定的中心按一定的方向转动，旋转中图形（物体）上任意一点的运动轨迹都是圆或圆的一部分。旋转有中心、方向、角度三个要素，运动方向有顺时针和逆时针两种。旋转时，既可以围绕一个点，也可以围绕一根轴;既可以旋转一圈或几圈，也可以旋转不足一圈。

平移和旋转，由于构成运动的要素不同，所以分开看彼此之间似乎没有联系，但其实不然。教学中，要引导学生沟通比较，启发学生建立联系，感悟不同运动方式的相同之处，即无论是直直地移动还是绕中心转动，运动中只是位置发生变化，形状和大小都保持不变。当然，这一整体性的认识还只是初步的，需要在之后的学习中进一步体验与理解。

（二）分析学情，明确教学重点

苏教版小学数学三年级上册《平移和旋转》一课是认识平移和旋转的起始课。教学前，学生并不是一张白纸，他们在日常生活和学习中有接触、有感知，但大多都是模糊的、未经数学化的。笔者在即将执教的一个班级做了前测，要求学生说说“什么是平移？什么是旋转”，并用文字或图示描述自己的理解。有學生认为：“平移就是平着运动，旋转就是转圈。”有学生举例：“火车往前开是平移，摩天轮转圈是旋转。”有学生比画：“走路就是平移，玩转圈游戏就是在做旋转运动。”大多数学生能将物体平移，也能将物体旋转，但对平移、旋转前后的变化感受不深。这些前概念是学生建立平移和旋转概念的重要基础。本节课就是要帮助学生从“模糊的感知”走向“清晰的认识”，引领他们体会相关运动的特点，感悟图形变换的本质，从而发展空间观念。

二、基于数学本质的教学

（一）多元表征，积累经验

数学本质的体会需要基于对相关现象的充分感知。教学中，一方面，要从学生已有的经验出发，从生活中撷取那些学生熟悉的、感兴趣的素材，引导学生通过观察、想象、比较、分类、交流等方式获得对平移和旋转概念的直观认识，生成两种运动的表象;另一方面，可以借助比画（动作表征）、画图（图像表征）及描述（符号表征）之间的关系，逐步提炼出相关运动的基本过程和主要特点，发展用数学的眼光观察现实世界的意识，为进一步体会平移和旋转的本质积累活动经验。

1.动作模拟，初步感知

教学伊始，教师出示一幅国旗上升图，询问学生看到这样的场景有什么感受，并让学生尝试比画和描述国旗的运动。学生感受到国旗是从下往上直直地上升的。教师以此揭示本节课研究的就是物体的运动方式。

接着，教师出示一些物体运动的图片（如下页图1所示），引导学生根据刚才的经验，用手势和语言描述出它们的运动。学生独立尝试并与同桌交流。教师巡视，选择一些典型的手势在全班交流，并引导学生在直观观察的基础上用语言来描述运动的过程。例如，模拟观光电梯运动时，可以把手放平，再沿着竖直方向从上往下或由下往上慢慢移动，移动的过程中不能晃动，要直直地移动;模拟风扇叶片旋转时，可以用手指在空中不停地画圈，尽量画得圆一些，还要说出是围绕着中心画的。

2.画图示意，自主分类

在用手势和语言描述物体运动的基础上，教师提出更高的活动要求：（1）你能用简单的符号或图形表示这些运动吗？（2）和同伴交流，将这些物体的运动方式分分类。

大多学生能够依据经验画图表示这些运动，在表示①③⑤时，学生都用直直的箭头，但画出的方向不同，有的是水平的，有的是竖直的，还有的是斜向的;在表示②④⑥时，学生都注意到要围绕着中心转动，但有的是围绕一个点转动，有的是围绕一条轴转动。学生互相补充想法，修正自己的作品。

在对六幅图所表示的运动方式进行分类时，学生出现了不同的意见：第一种分为3类，即①⑤一类，②④⑥一类，③单独一类;第二种分为2类，即①③⑤一类，②④⑥一类。教师询问各自分类的理由，引导学生着重讨论扶手电梯的运动：它也是直直地在移动，只不过是向着斜方向移动的。在辩论中，学生达成共识，一致认为分为两类较为合适：一类都在直直地运动，只是方向不同;另一类都是围绕一个点或一条轴转动。

（二）比较归纳，探寻本质

人类社会中几乎所有的概念都是抽象的结果。从数学本身的发展来看，数学概念的来源有两个：一是直接由客观事物的数量关系和空间形式反映而得;二是在抽象的理论基础上经过多级抽象所得。本节课学习的平移和旋转显然属于前者。教学中，需要遵循“先直观后抽象”的原则，引导学生在比较中将空间思维向更深处迈进。其一，对平移要抓住“直直地”“移动”这两个关键属性，对旋转则要抓住“固定点（轴）”“转动”这两个关键属性。其二，通过对比两种运动方式，促使学生感悟：无论是直直地移动还是绕固定点或轴转动，物体本身保持不变。

1.分层揭示，抽象概括

（1）理解平移

教师引导学生再次观察观光电梯、扶手电梯和窗户的运动，讨论这些运动有什么相同与不同之处，揭示像这样沿着直线从一个位置移动到另一个位置的运动叫作平移，可以水平平移、垂直平移，也可以斜向平移。

接着，教师启发学生思考怎样能清楚地描述物体的平移运动，在交流中逐步聚焦平移的方向和距离这两个要素，且明确物体在运动中只是位置发生变化，形状和大小都不变。

（2）理解旋转

教师引导学生再次观察风扇叶片、飞机螺旋桨和地球仪的运动，鼓励学生依据刚才认识平移概念的经验，交流讨论这类物体运动方式的特点，得到旋转的概念，明确旋转运动的物体都是绕着一个固定点或一条固定轴转动的，可以顺时针转动，也可以逆时针转动，而且运动中只是位置发生变化，形状和大小都不变。

2.判断说理，举例说明

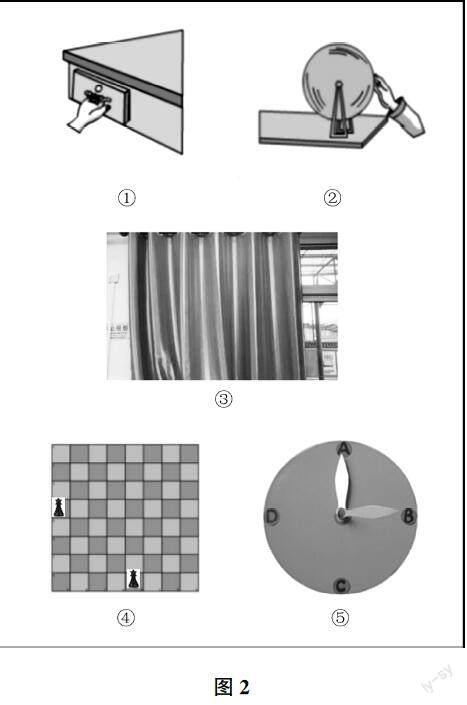
教师出示五幅图片（如图2所示）让学生进行判断：说出是平移还是旋转，并说明理由。学生回答后，教师适时指出：刚开始的时候，我们凭借生活经验知道这样的运动是平移或旋转;学到这儿，我们要能依据它们各自的特点进行判断和解释。接着，教师让学生举出一些生活中平移或旋转现象的实例，注意纠正学生举例中不规范的表达。

需要提及的是，这里引入了拉窗帘的运动，这一运动极具欺骗性，能够很好地暴露学生的学习情况：没有深刻理解平移本质的学生很容易错认为它是平移。教师在巡视过程中有意识对此题进行了观察和统计，发现大多数学生能够作出准确的判断。

3.回顾反思，建立联系

在此基础上，教师引导学生回顾刚才研究的方法：我们首先观察，然后通过比画和画图想象，接着比较这些物体的运动方式，又通过分类认识了平移和旋转各自的特点;观察、想象、分类等都是我们学习数学常用的方法。

接着，教师引导学生经历在变化中寻求不变的过程，启发学生将平移和旋转两种不同的运动建立联系，感受到：平移是物体从一个位置沿着某一方向直直地移动到另一个位置，旋转是物体围绕一个固定点（轴）转动，这是它们的不同之处;而平移和旋转都是全等变换，也就是运动前后图形（物体）的形状、大小都没有改变，只是位置发生了变化，这是它们的相同之处。

（三）自主操作，丰富内涵

本节课虽然只是初步认识平移和旋转现象，但并不意味着教学过程就只能停留在表面。比如，旋转的“转”是显而易见的，但是学生时常会忽视旋转中心这一要素，以至于认为“旋转就是转”，而意识不到是绕着什么在转。事实上，操作是获得直观感受的有效途径，也是构建空间观念的重要方式。我们可以通过开展各种形式的操作活动，引导学生在直观感受中不断提升思维层次，逐步丰富概念的内涵。

1.平移操作

教师出示操作要求：把长方形纸片放在数学书的左上角，然后把它平移到右下角。

反馈中，有的学生先用长方形的长边贴着数学书的上边平移，再用短边贴着右边平移;有的学生则先下移，再右移。学生意识到，两种操作方式皆可，只要在移动的过程中保持这种状态。此外，有的同桌互相配合，一人借助直尺確定好直接平移的轨迹，另一人把长方形纸片从数学书的左上角平移到右下角。这样做突出了长方形纸片是沿着直线运动的。

将长方形纸片从左上角平移到右下角，学生给出了两种不同的操作路径。路径一是通过两次平移得到，先往右再往下或者先往下再往右;路径二是通过一次平移得到，从左上角斜斜地移到右下角。在不同平移方法的比较中，学生认识到无论朝哪个方向移动，都要沿着直线运动，而且加深了“斜向移动也是平移”的认识。

2.旋转操作

教师出示操作要求：用毛线或者其他物品创造一个旋转运动。

反馈时，引导学生对两名同学用毛线展示的旋转运动进行思考：比较两种转法有什么相同和不同的地方。学生发现：相同之处是紧紧按着毛线，围绕着一个中心转动;不同之处是可以顺时针旋转，也可以逆时针旋转。

教师出示毛线与橡皮的旋转运动，继续让学生感悟旋转的特点，加深对旋转内涵的理解，引导学生发现：旋转时中心点是固定不动的，旋转时既可以旋转一圈或几圈，也可以旋转不足一圈，还可以围绕一个中心来回摆动。

（四）学以致用，感悟价值

本节课的最后一个环节，意在通过一些综合练习促使学生深度思考，总结平移和旋转的特征，继续感悟两种运动方式的数学本质。需要关注的是，虽然平移和旋转没有平面图形、立体图形的形状、大小等静态要素，但教学中要将平移和旋转两种运动与之前的学习建立联系，让学生感受知识之间的融通，还要拓展平移和旋转的实际意义，使其充分感受两种运动的实际价值，为后续研究图形的运动做好准备。在这一过程中，对学生的要求从能判别物体的运动方式上升到能自主构建出两种运动，这对学生的空间想象能力是一次巨大的挑战。

1.综合练习，深化认知

教师出示第1题：

图3中哪些树叶只通过平移就可以和图4中的树叶重合？

在学生找出符合要求的树叶之后，教师引导他们观察平移后能重合的树叶有哪些相同之处，在平移的过程中有什么不同，继续强化对平移前后物体的大小、形状不变，而平移的方向和距离不同的认识。进一步地，引导学生观察②号和④号树叶，发现将其先旋转再平移或先平移再旋转也可以和图4中的树叶重合，体会有时要用到两种运动方式。

教师出示第2题：

不能由“”通过旋转得到的是（）？

A. B. C.

学生交流发现，将所给图形顺或逆时针旋转180°得到图B，将所给图形顺时针旋转90°得到图C，而图A中圆和正方形在一边（连在一起），形状发生了变化，因此无法通过所给图形旋转得到。

2.瞻前顾后，感悟价值

除了让学生感受到本节课研究的平移和旋转与生活密切相关，还应从更为理性的层面帮助学生拓展研究平移和旋转的意义。

教师提问：在以前的学习中有没有用平移和旋转解决过问题？然后出示苏教版小学数学二年级上册练习三中的习题（如图5所示），引导学生通过回顾与交流，感受把两个完全相同的三角形拼成平行四边形的过程中包含平移和旋转（如图6所示），将新知与旧知建立关联。

此时，学生的思维被打开，教师适时引导学生想象，只要用运动和变化的眼光观察学过的一些图形，通过平移和旋转，就会得到不一样的图形（如图7所示）。通过课件演示，如点通过平移得到线，线通过平移或旋转得到面，面通过平移或旋转得到体，学生在观察、想象、描述的过程中认识到，图形经历不同的运动，可以得到平面图形，还可以形成立体图形，感受图形变换的神奇与奥妙，体会平移和旋转的价值，借由生动的运动转向更为深入的思考。

参考文献：

[1] 史宁中.基本概念与运算法则——小学数学教学中的核心问题[M].北京：高等教育出版社，2013.

[2] 鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.6-11