辩论：数学课堂的美丽风景

朱华

［摘 要］将“辩论”适时引入小学数学课堂，符合新课程理念，且能够改变传统的从教师到学生的单向式输入模式，使师生交流、生生交流更加丰富多样。在教学重点处、难点处、意外生成处以及学生思维受阻处展开辩论，有利于提高学生对知识的认知深度，发展学生的思维能力，提升学生的数学学力。

［关键词］辩论；思维；意外；小学数学

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）29-0036-03

课程标准明确指出，教学活动是师生积极参与、交往互动、共同发展的过程。由此可见，课堂教学应该是教师的教与学生的学相互统一的过程，是师生之间、生生之间相互交流、思维碰撞的过程。 数学学科具有很强的逻辑性和严密性，从某种意义上来讲，学习数学的过程就是一个“说理”的过程。“ 灯不拨不亮，理不辩不明”，将辩论适时引入小学数学课堂，能够改变传统的从教师到学生的单向式输入模式，使师生交流、生生交流更加丰富多样。“辩”是为了认识真理，“论”是为了捍卫观点，辩论的目的在于辨真伪、论是非、究事理。通过辩论，学生可以充分表达自己的观点，可以在“短兵相接”和“唇枪舌剑”中提升对知识的认知水平，发展思维能力，提升数学学力。

一、辩论式教学的特点

辩论式教学是一种具有较强综合性的教学方法，它以学生为主体，由小组成员或者全班学生围绕特定辩题各抒己见，在辩论中主动获取知识、发展素养。辩论式教学具有主动性、互动性和综合性的特点。（1）主动性。在辩论式教学中，学生通过讨论、争论获得知识，大胆发表自己的观点和看法，聆听对方意见，判断正误，从而成为课堂真正的主人。（2）互动性。在辩论活动中，学生一般分为正方和反方，这加强了生生之间、师生之间的互动交流，这种互动交流能够帮助学生克服自我中心意识，培养思维的深刻性和灵活性。（3）综合性。辩论活动将启发、倾听、质疑、暗示、表达、提问、讲解等融为一体。在辩论过程中，学生认真倾听对方观点，找到其中破绽，从而适时质疑、提问，并修正、完善自我认知。

二、辩论的价值

首先，辩论能够让学生的数学表达更加清晰。“语言是思维的外壳。”数学学习的过程可以看作是一个语言学习的过程。教师应当将让学生熟练掌握数学语言作为重要的教学目标，使学生学会数学表达，强化学生对数学的理解等。辩论能让学生的数学表达更加清晰。

其次，辩论能够让学生更加主动地投入学习。现代教育理念认为，学习的过程是一个自主建构的过程。要从根本上实现“意义赋予”和“自主建构”，需要学生相对独立地、积极主动地投入学习当中。通过辩论，可让学生由“被动地听”转向“主动地说”和“数学地谈论”，让学生之间充分地互动、交流、辩驳、批判、反思、改进，最终让学生主动参与到知识建构当中。

最后，辩论能让学生发现自己。每一个学生都是一个独立的个体。教育的根本目标是“让每一个学生成为他自己”。在数学课堂中适时展开辩论，可让学生自信地阐述自己的观点，在“百家争鸣”的氛围中实现自我价值。此外，辩论还能够刺激学生的兴奋点，将课堂氛围推向高潮。

三、基于辩论的小学数学教学实践路径

1.在教学重点处辩论，培养思维的深刻性

“举网以纲，千目皆张”的意思是提网的时候要提起大绳子，这样一个个网眼就都张开了，这句话经常用来比喻做事情要条理分明，抓住重点。教学亦同此理。每一节课都有要求学生重点掌握的知识，学生在理解这些知识时可能会陷入思维误区，教师就可为学生提供丰富的学习和探究材料，引导学生对重点知识进行辩论，从而使学生深刻理解知識。

比如，在“小数的认识”这节课中，小数的基本性质（小数的末尾添上零或者去掉零，小数的大小不变）是学生需要掌握的重点知识。由于受思维水平和认知方式的限制，学生在理解此知识点时出现了分歧。综合学生的观点，基本可以分为两种：一种是认为0.1=0.10，另一种是认为0.1<0.10。为了使学生能够甄别对错，厘清本质，笔者组织学生进行辩论。笔者将学生分为正方（认为0.1=0.10）和反方（认为0.1<0.10）。

反方：我认为0.1<0.10。因为在比较整数的大小时，两位数的整数大于一位数的整数，按照这样的规律，0.1是一位小数，0.10是两位小数，一位数的小数应小于两位数的小数，所以0.1<0.10。

正方：我不同意。在比较小数大小时，应该把整数部分和小数部分分开比较。先比较整数部分，如果整数部分相同，再比较小数部分；小数部分从十分位开始比，如果十分位相同，再比较百分位，以此类推。小数点后面末尾的0可以去掉，所以0.1=0.10。

反方：在比较整数的大小时，整数末位的0不能随便去掉，为什么在比较小数的大小时却要去掉末尾的0呢？

……

正方：可以把小数转化成分数再比较大小。0.1转化成分数是1/10，0.10转化成分数是10/100，因为1/10=10/100，所以0.1=0.10。

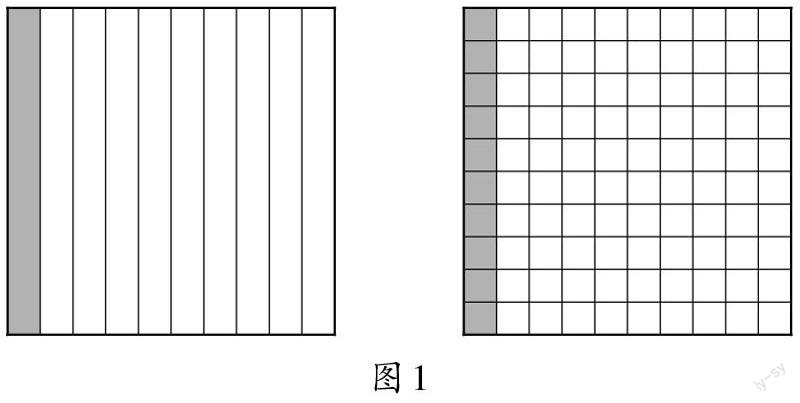
正方：也可以通过画图来论证。用一个正方形表示单位“1”，0.1表示把这个正方形平均分成10份，取出其中的1份；而0.10表示把这个正方形平均分成100份，取出其中的10份。从图（如图1）中不难看出，这两部分（涂色部分）的大小是相同的，所以0.1=0.10。

教学中，教师在教学重点处适时安排计数学辩论，给予了学生自由表达观点的时间和空间。持不同观点的学生为了论证自己的观点“各显神通”，或对比，或画图。正是在这样你答我辩的激烈交锋中，学生的个性得到了张扬，学生对新知的理解得到了深化。

2.在教学难点处辩论，培养思维的批判性

在教学中，学生不易理解的知识是教学难点之所在。突破教学难点的方法有很多，适时引入课堂辩论无疑是一种行之有效的方法。在教学难点处引入辩论，能够使学生充分表达自己的理解和困惑，让学生的数学思维具有可见性，让学生不断地思考、修正、完善自己的认知偏差，激活和显现内隐的思维过程，从而形成具有批判性的思维。

比如，在教学“异分母分数的加法”时，教师引导学生计算“1/2+1/3”，结果有的学生只是简单地把分子与分子相加，分母与分母相加，得出“1/2+1/3=1+1/2+3=2/5”，而且学生对这种计算方法深信不疑。为了使学生辨对错、明是非，笔者适时引入课堂辩论。

反方：我认为1/2+1/3=2/5，因为在计算同分母分数相加时，就是直接把分子相加的。

正方：不对。现在分母不一样了，不能按照原来的方法计算了。

正方：我们从数据上也可以发现这样计算是错误的。如果1/2+1/3=2/5，2/5比1/2还要小，怎么可能越加越小呢？

反方：整数的加法计算就是个位与个位相加作为得数的个位，十位与十位相加作为得数的十位，那现在不应该是分子加分子作为得数的分子，分母加分母作为得数的分母吗？

正方：我认为异分母分数加法之所以不能直接把分子与分子相加，分母与分母相加，是因为分数单位不一样。

正方：正是因为分母不同，导致分数单位不同，所以不能直接相加。

反方：我还是不理解。

正方：比如5米和4厘米能直接相加吗？8元和6角能直接相加吗？

反方：当然不能。

正方：同样的道理。1/2和1/3分母不同，其分数单位也不同，所以不能直接相加。

师：那应该怎样转化才能计算呢？

正方：应该用通分的办法，把异分母分数转化为同分母分数，这样就能按照同分母分数加法进行计算了。

“真理越辩越明。”教学中，当学生对“为什么异分母分数相加时不能把分子与分子直接相加，把分母与分母直接相加？”这一问题感到困惑时，教师并未急于给出答案，而是把学习、思考的主动权交给学生，为学生营造了辩论的氛围。学生为了论证自己的观点，使出浑身解数，从不同角度来阐释思路，这就激活了学生的思维，使学生的思维更具发散性和批判性，提升了学生的思维品质。

3.在思维受阻处辩论，培养思维的严谨性

数学具有较强的逻辑性和抽象性，而小学生以形象思维为主，这就使得小学生在认知、理解数学知识时经常感到力不从心，出现思维卡壳的情况，如果不能引导他们冲破思维障碍，就会影响他们对知识的理解。因此，在学生思维受阻处适时引入辩论，可以丰富学生的数学学习体验，提升学生思维的严谨性。

比如，在教学“平行四边形的面积”时，教师给学生出示这样一道题：把一个长方形拉成一个平行四边形，四条边的长度不变，它的面积怎样变化？学生有的说面积变大了，有的说面积变小了，还有的说面积没有变化。本题要求学生除了要熟悉平行四边形、长方形的面积计算公式，还要有一定的空间想象力。学生在问题解决路径上产生了分歧，并且各执一词，各不相让。面对这种情况，教师组织学生进行辩论。

小组一：我认为把长方形拉成平行四边形后，它的面积不会发生变化。因为它的四条边的长度都没有发生变化，面积当然不会发生变化。

小组二：四条边的长度没有变化，只能说明周长没有改变，与面积没有关系。

小组三：我认为把长方形拉成平行四边形后，面积变大了。因为平行四边形是斜着的，它占的面积更大些。

小组四：我不同意。长方形的面积等于长乘宽，平行四边形的面积等于底乘高。把一个长方形拉成一个平行四边形，它的底没有发生变化，但是高却变短了（如图2），所以它的面积应该是变小了，而不是变大了。

上述教学中，教师在学生的思维受阻处引入辩论。通过辩论，学生对平行四边形面积的认识更加深刻了，学生思维的逻辑性和条理性也得到了培养。更为重要的是，学生通过辩论，把“被动地听”转化为“主动地说”，在思维碰撞中完成了对知识的自主建构。

4.在意外生成处辩论，培养思维的创造性

由于思维之间的差异性，不同的学生对于同一知识会有不同的理解，这就注定了教学不可能一成不变，而是一个随时可能碰到“意外”的动态发展过程。教师只有学会从容地面对“意外”，巧妙地利用“意外”，才能打造出别具特色的精彩课堂，培养学生思维的创造性。

比如，在教学“体积与容积”时，教师引导学生通过举例来说明体积的内涵。学生举出黑板、课桌、人、凳子等都有体积。这个时候，一位学生問道：“一张纸有体积吗？”这突如其来的一问，着实令教师有些措手不及，但教师抓住机会，及时引导学生展开辩论。

反方：一张纸那么薄，根本没有体积。

正方：不对，一张纸很薄，只能说明它的体积小，不能说它没有体积。

反方：一张纸不是立体图形，怎么会有体积呢？

正方：我们可以试想，把成百上千张纸叠在一起，那么厚的一摞纸肯定有体积。对吗？

反方：对。

正方：既然一摞纸有体积，那么，一张纸肯定也有体积。

正方：我们还可以这样理解，把一张纸多次对折，它就会变得厚实起来，它的体积就会显现出来，所以一张纸也是有体积的。

“教者有心，学者得益。”教学中，面对学生的意外之问，教师及时捕捉了学生思维中瞬间生成的精彩火花，不失时机地点燃了学生的辩论热情。在想方设法论证自己观点的过程中，学生加深了对知识的理解，思维的创造性也得到了培养。

如果说“听”是一种内隐的思维灵动，那么“辩”就是一种外在的、活泼的思维碰撞。辩论并非目的，辩论是一种学习手段，辩论是一种学习工具，辩论是一个学习过程。在课堂辩论中，教师要抓住时机，选择恰当的辩题，引领学生碰撞思维，促使学生交融智慧，让课堂显现精彩和魅力，让课堂充满睿智和思辨！

（责编 黄春香）