关注探理过程，培养运算能力

2022-05-30华秀祥

小学教学参考(数学) 2022年10期

华秀祥

［摘要］以“异分母分数加减法”的教学为例，引导学生有序地探索异分母分数加减法的算理。从初识算理、理解算理到沟通算理，提升学生运算能力的同时，帮助学生构建完整的知识体系。

［关键词］异分母分数；加减法；运算能力

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）29-0066-03

培养学生的运算能力是小学数学教学的重要任务之一。在运算教学中，教师除了要遵循数学教学的一般规律，最重要的是引导学生探明算理。以“异分母分数加减法”为例，笔者在教学中引导学生探索异分母分数加减法的算理，厘清知识之间的内在联系，把单一的知识点串成链条、编织成网，在提升学生运算能力的同时，帮助学生构建完整的知识体系。

一、算理教学的意义

在运算教学中，引导学生探明算理，对发展学生各方面能力具有重要意义。首先，算理教学有助于学生运算能力的提升。在传统的计算教学中，学生往往都是机械式地死记硬背运算的步骤和法则，这就使得颇具思维含量的数学运算退变为机械的数字操作，不利于学生运算能力和数学思维的培养。在算理教学中，教师引导学生通过相关操作推导、理解算理，在算理与算法之间搭建桥梁，使学生自主构建算法。这样一来，学生对运算过程的理解就要深刻得多。其次，算理教学有助于学生积累数学活动经验。在探究算理的过程中，学生通过观察、操作、分析、推理、归纳等活动，经历知识生成的过程，体验获得知识的喜悦，积累了数学活动的基本经验。最后，算理教学有助于培养学生的抽象思维。学生在理解算理时，往往要经历一个从具体形象到概括抽象的过程，必要时还会借助相关的实物操作或直观模型来辅助理解，这对于学生的思维由形象思维向抽象思维转变具有重要的推动意义。

二、注重探明算理，培养运算能力之操作路径

1.在情境中产生探究算法和算理的意愿

课程标准指出，学习材料的选择要立足学生的实际生活，有利于学生体验和理解、思考和探索。小学生的思维方式以形象思维为主，因此，学生理解抽象的算法和算理具有一定的困难。教学中，教师可将数学知识巧妙地与现实生活情境相关联，激发学生的学习兴趣和探求欲望，从而让抽象的数学知识变得生动起来，为学生的认知和理解做好铺垫。

【教学片段1】

师：今天是淘气的生日，妈妈为淘气买了一个生日蛋糕。淘气吃了这个蛋糕的1/2，妈妈吃了这个蛋糕的1/4，他们一共吃了这个蛋糕的几分之几？

生₁：列式为1/2+1/4。

生₂：对，然后直接计算就可以了。但是怎么跟我们以前学的分数加法不一样啊？它们的分母不同，这可怎么计算呢？

生₃：1/2+1/4=1+1/2+4=2/6。

师：生3的算法对不对呢？就让我们一起开启探索之旅吧！

以“吃蛋糕”的生活情境引入新课，把异分母分数相加蕴藏在生活情境中，为学生进一步探索算理提供了现实基础。同时，学生真切地体会到异分母分数加减法并非纯粹的理论知识，而是源于现实生活中解决实际问题的需要，进而产生学习动机。

2.在探索中掌握算法、了解算理

探索的过程是一个动态、开放的过程。教师要正确处理“收”和“放”的关系，引导学生在探究算理的过程中把抽象的算理转化为直观的图形，使学生更加深刻地理解知识，明了算理。

【教学片段2】

师：对于1/2+1/4=1+1/2+4=2/6，大家认为对吗？

生（齐）：不对。

师：谁能说说这种算法为什么不对呢？

生₁：如果1/2+1/4=1+1/2+4=2/6，那么，2/6=1/3，1/3＜1/2，1/2+1/4＜1/2，这不是互相矛盾了吗？一个数怎么会越加越小呢？

生₂：是啊，看来这种直接把分子和分母加起来作为新的分子和分母的算法是不对的。

师：这道题应该怎么计算呢？大家尝试用自己的算法做一做。

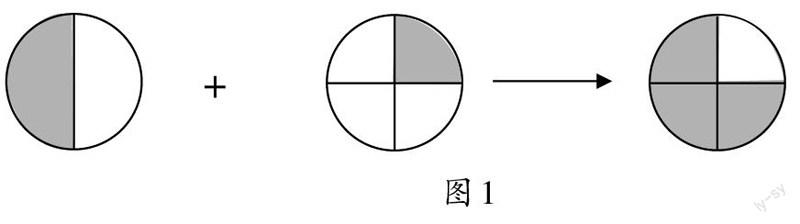
生₃（出示图1）：我是用画图的方法来计算的。我在两个同样大小的圆里分别画阴影表示1/2和1/4，这样，加在一起的阴影部分占了這个圆的3/4。1/2和2/4在大小上是相等的，所以1/2+1/4就转化成了2/4+1/4，2/4和1/4的分数单位都是1/4，可以直接相加，即1/2+1/4=2/4+1/4=3/4。

师：生₃通过画图的办法把异分母分数相加转化为同分母分数相加。还有其他算法吗？

生₄：我先把一张纸对折一次，这张纸就被平均分成2份，给其中一份涂上红色，就是1/2；我再把纸对折一次，这张纸就被平均分成了4份，我给其中一份涂上红色。把纸拆开后发现，涂红色的部分一共占了这张纸的3/4，因此，我得出1/2+1/4=3/4。

师：生₄是通过折纸的办法来计算的，这个办法和画图的办法有异曲同工之处，本质上是一样的。

生₅：我是这样计算的——先把分数1/2转化为小数0.5，然后把分数1/4转化成0.25，这样1/2+1/4=0.5+0.25=0.75=3/4。

师：这种把分数转化成小数的办法就是把未知转化为已知。这种办法不错，的确是可行的。

生₆：我是用通分的方法做的。1/2+1/4=2/4+1/4=3/4。

生₇：为什么要把1/2转化成2/4呢？

生₆：2/4就是2个1/4，再加上1个1/4，就是3个1/4，因此1/2+1/4=2/4+1/4=3/4。

师：这是通分的办法。

在探究过程中，每个学生都是一个具有鲜明特色的思维主体，不同层次的学生从自身认知出发，在独立思考的基础上，收获属于自己的算理。在探究之初，教师先引导学生发现把分子和分母直接相加是错误的做法，再鼓励学生进行自主思考和探索。画图法和折纸法使学生直观地体验到分母由2变为4的基本过程，通过数形结合把抽象的通分过程生动地展现出来；把分数变为小数的办法，则充分结合了学生已有的知识和认知经验，打通了分数与小数之间的“关节”，提升了学生的整体性认识。学生不但能够展示算理，还能够通过互相交流，理解和借鉴其他学生提出的算理，从而丰富自己的认知，更加全面地感知算理。

3.在比较中优化算法、理解算理

在学生初步了解算理的基础上，教师应当引导学生对各种具体算法进行比较，使学生在比较中知对错、明优劣，逐渐经历从“慢法”“笨法”到“快法”“巧法”的转变，在对比中凸显通分法的优势，并自然而然地把方法转移到通分法上。比较和取舍既是学生学习新知识要经历的环节，也是学生更加深刻地理解算理的现实需要。需要注意的是，教师不要简单地直接告知学生哪种算法是最优化算法，而是要让学生在实际运用当中去比较、感悟、选择，逐渐把目光聚焦到通分法上。

【教学片段3】

师：我们找到了四种计算异分母分数相加的方法，分别是画图法、折纸法、转化法和通分法。哪种方法最好呢？我们在应用中感受一下。首先来看画图法和折纸法。

师：请同学们用画图法和折纸法计算3/4+1/8。

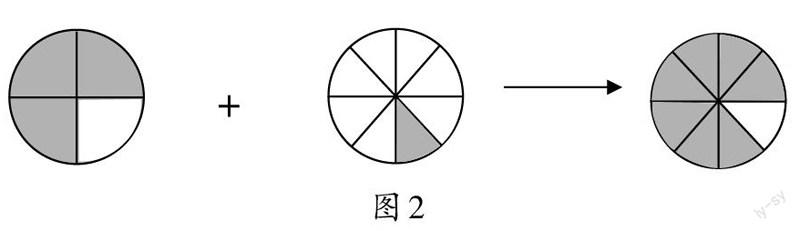
生₁（出示图2）：这是我画的图。通过画图得出3/4+1/8=6/8+1/8=7/8。

师：通过画图，你有什么体会？

生₁：分母越大，画图就越麻烦。这道题中分母最大是8，我需要把圆平均分成8份，如果分母是16，我就需要把圆平均分成16份，那样太麻烦了。

生₂：是呀，我也有这种体会。在分母不大的时候，画图法还可以，可是分母越大，画图法就越不方便。

生₃：折纸法也是这样。分母是8，我需要把一张纸对折三次，这勉强还可以做到，如果对折四次或是更多次，就非常困难了，而且数的时候也容易出错。

师：看来，画图法和折纸法尽管非常直观，但是它们的操作过程比较麻烦，实用性并不强。我们再来看转化法。请大家用转化法计算1/2+1/3。

生₄：1/2可以转化成0.5，但是1/3转化成小数后，是一个无限循环小数，这样很难得到精确的结果。

生₅：这道题用转化法行不通，看来这种方法也有局限性。

师：画图法、折纸法、转化法都有局限性。请试着用通分法算3/4+1/8和1/2+1/3。