立足经验，经历过程，促进深度理解

赵海

［摘 要］以“小数的意义”的教学为例，立足新课程标准，提出促进学生深度理解知识的有效路径，即立足经验，把握学习起点；丰富经验，理解小数本质；拓展经验，深化学生理解，以使学生获得深刻的数学理解，促进学生在思维和能力方面的进步和发展。

［关键词］小数的意义；经验；过程；理解

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）29-0057-03

课程标准提出，数学教学要从学生的已有经验出发， 让学生亲身经历将实际问题抽象为数学模型并进行解释与应用的过程，进而使学生获得对数学理解的同时， 在思维能力、 情感态度与价值观等方面得到进步和发展。建构主义理论认为，所有的知识都是在已有知识和经验的基础上建构起来的。因此，在教学中，教师要立足学生的已有经验，将学生的已有经验作为教学的起点，从而促进学生对知识的理解。

特级教师俞正强在《小学数学课堂学习的起点在哪里》一文中指出：“在学习目标既定的情况下，起点的选择决定着认知发展过程的距离长短。”要实现科学的“起点的选择”，就需要教师基于学生的已有经验，使数学教学有效对接学生的已有经验，由此降低数学学习坡度，优化数学知识的呈现方式，让学生体会数学学习的愉悦感。

一、立足经验，把握学习起点

美国教育心理学家奥苏泊尔说 ：“影响学习的唯一重要的因素就是学习者已经知道了什么。”学生的学习起点是数学教学活动展开的基础和前提。学生在学习新知识之前并非一张白纸，他们已经具有一定的知识储备和生活经验，这是学生学习新知识的现实基础。教材将“小数的认识”分为两个阶段：第一阶段，主要是依托模型并結合具体情境来认识小数；第二阶段，学生已经初步认识了小数，因此这个阶段主要是沟通分数与小数的联系，实现分数与小数的互相转化，引导学生脱离具体情境，从更高层次上认识小数，从而对小数的认识由“形式模仿”走向真正的“意义理解”。第二阶段的学习是以第一阶段为基础的。因此，在“小数的意义”一课中，教师要注意立足学生已有的知识储备和生活经验，从而精准把握学生的学习起点。

【教学片段1】

师：星期天，淘气到商店去买东西，他看到某种商品的价格为1.11元/千克。那么，1.11元是多少钱呢？

生₁：我们已经学过了，0.1元是1角，0.01元是1分，所以1.11元是1元1角1分。

师：我们现在已经初步认识了分数，你能用分数来说一说1.11元的含义吗？

生₂： 1角是1元的1/10，也可以写成0.1元；1分是1元的1/100，也可以写成0.01元。

师：1/10元 = 0.1元，1/100元 = 0.01元。1/10与0.1之间，以及1/100与0.01之间是什么关系？

生₃：相等。1/10 = 0.1，1/100 = 0.01。

师：你能用相同的思路解释1.11米的含义吗？

生₄：我知道1.11米等于1米1分米1厘米。1分米是1米的1/10，也可以写成0.1米；1厘米是1米的1/100，也可以写成0.01米。

生₅：同样可以得出1/10 = 0.1，1/100 = 0.01。

教育家杜威认为，一盎司经验胜过一吨理论。教学中，教师借助人民币和长度单位的生活模型，引导学生解释1.11元和1.11米的含义，这就充分激活了学生已有的认知经验，唤醒了学生对“1角= 0.1元，1分 = 0.01元；1分米 = 0.1米，1厘米 = 0.01米”的知识记忆，还帮助学生理解了“1角是1元的1/10，1分是1元的1/100；1分米是1米的1/10，1厘米是1米的1/100”，进而使学生感知小数与分数的关系，初步理解小数本质上是分数的另一种表现形式。

二、丰富经验，理解小数本质

学生理解数学概念是一个循序渐进、逐渐深入的过程。认知心理学研究结果证实，概念的形成其实可以分为两个阶段， 即从完整表象上升为抽象概念，实现抽象概念在思维过程中的具体再现。如果把抽象的概念看作种子的坚硬外壳，怎样才能让其变得柔软呢？最好的办法就是对接学生的已有经验，用直观形象的表述，用有生命温度的数学活动，像水一样软化种子的坚硬外壳，从而直抵概念的内核。小数的概念是抽象的，在立足于学生的基本经验，引领学生借助生活情境和生活模型实现了对小数的初步认识后，教师应当进一步丰富学生的认知经验，引导学生从更深层次上理解小数的本质。在教学片段1中，学生是在模型的框架内认识1.11元和1.11米的，接下来教师就需要引导学生脱离具体的情境去感悟小数的本质，使学生更深刻地理解小数与分数之间的联系，感悟具有普遍适用性的小数的意义。

【教学片段2】

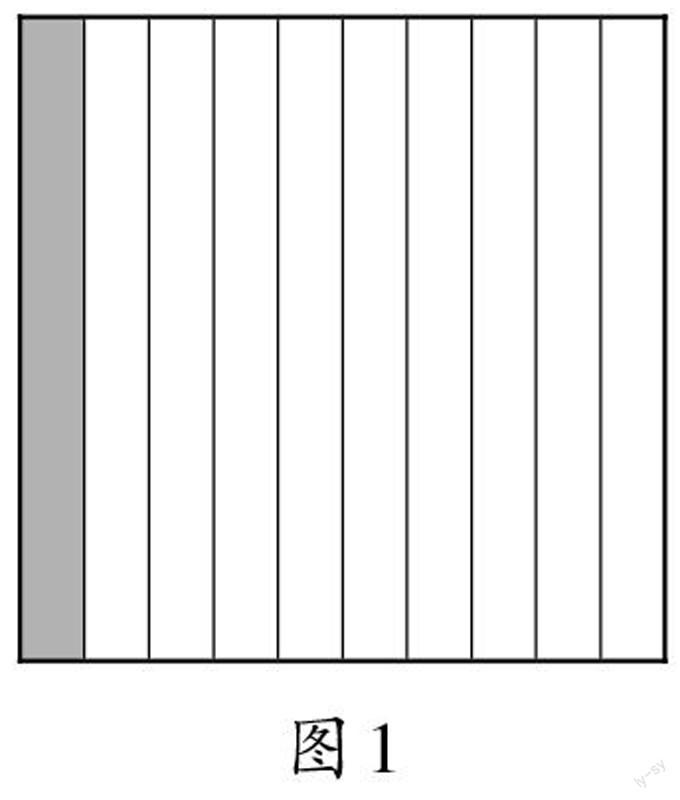
师：如果用1个正方形表示“1”，把它平均分成10份，其中的1份可以怎样表示呢？

生₁：其中的1份是1/10，也可以用小数0.1来表示。（出示图1）

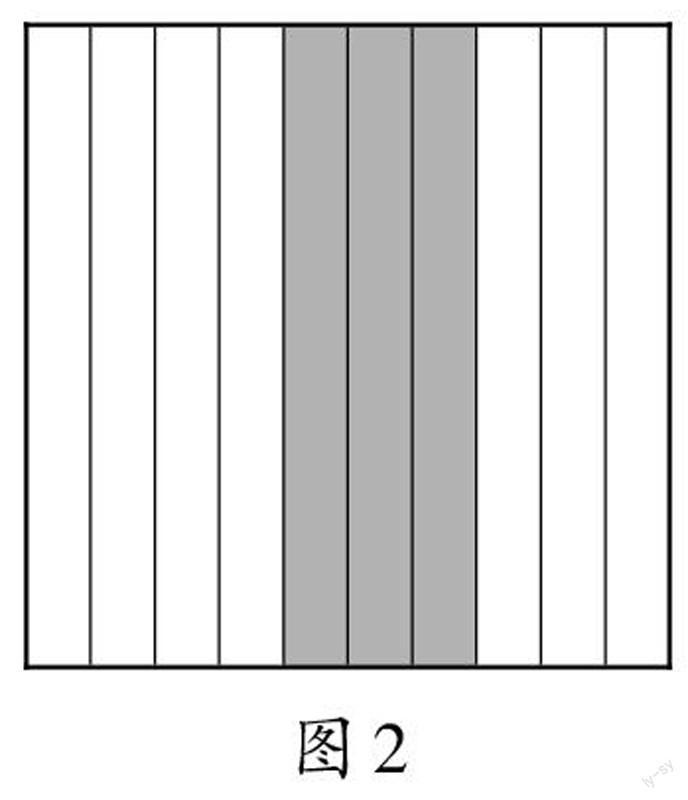
师：如果我要表示其中的3份呢？

生₂：其中的3份是3/10，也可以用小数0.3来表示。（出示图2）

师：0.7是怎样得到的？你能想象出这个图形吗？

生₃：0.7就是7/10，也就是把“1”平均分成10份，取出其中的7份。因此只需要把正方形中的7份涂上颜色就可以表示0.7了。

师：观察上面的数，说一说你的发现。

生₄：把“1”平均分成10份，其中的几份就是十分之几，用小数表示就是零点几。

生₅：这些分数的分母都是10。

生₆：分母是10的分数可以转化成一位小数。

师：如果用1个正方形表示“1”，将它平均分成100份，其中的1份怎样表示？

生7：其中的1份是1/100，也可以用小数0.01来表示。

师：如何表示其中的23份呢？

生₈：其中的23份是23/100，也可以用小数0.23来表示。

师：0.03是怎样得到的，能在百格图中画出来吗？

生₉：0.03就是3/100，也就是把“1”平均分成100份，表示其中的3份，所以只需要把正方形中的3份涂上颜色就可以表示0.03了。

师：观察我们分析过的数，你有什么发现？

生₁₀：这些分数的分母都是100。

生₁₁：分母是100的分数可以转化成两位小数。

师：如果把“1”平均分成1000份，其中的1份是（       ）/（       ），也可以表示为（ ）；其中的59份是（       ）/（       ），也可以表示为（ ）；其中的123份是（       ）/（       ），也可以表示为（ ）。

（学生思考并交流）

师：现在，你能说一说小数和分母是1000的分数间的关系吗？

生₁₂：分母是1000的分數可以转化成三位小数。

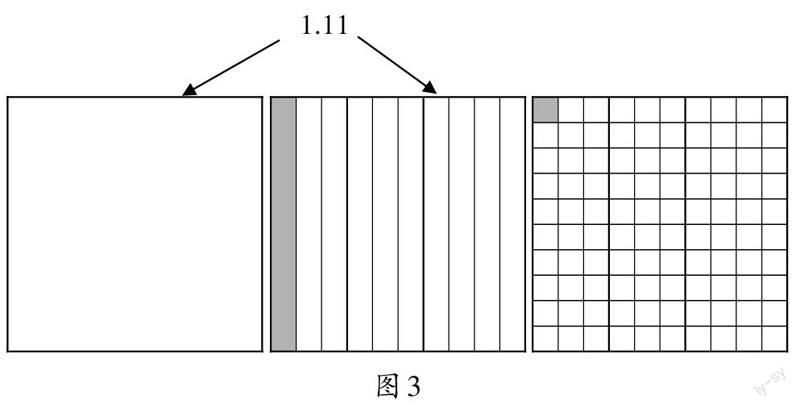
师：现在，如果把1.11元和1.11米的单位去掉，你能用图形表示“1.11”吗？

（学生探究后得出图3）

教学中，教师巧用格子图，简明地沟通了分数与小数之间的对应关系，并将这种抽象的关系通过图示具体、直观地表示出来，从而使学生逐渐摆脱具体情境和生活模型，从本质上理解小数的意义，使一位小数、两位小数和三位小数的关系在学生头脑中达成联结和深化，将数的抽象性和几何的直观性有机结合起来。

三、拓展经验，深化学生理解

从知识的产生和学生的认知规律来看，学生需要借助大量的现实情境做依托来理解小数的意义，但是如果学生的理解仅仅局限于具体的情境和模型，这样的理解是浅显的。因此，教师运用格子图使学生摆脱具体情境，进而从本质上理解小数的意义是极为必要的。然而，在笔者看来，教学还不能止步于此。因为小数的意义经常被运用在单位的转化中，而这又是学生容易出错的地方。因此，教师应该拓展人民币单位和长度单位模型，将小数的意义延伸到时间单位、面积单位和质量单位之中，只有这样才能让学生更有效地理解小数的意义，并能正确地运用小数的意义解决实际问题。

【教学片段3】

师：0.7时等于多少分呢？

生₁：根据0.7米 = 7分米，0.7元 = 7角，所以0.7时 = 7分钟。

生₂：不对。“0.7”的含义是把“1”平均分成10份，其中的7份是7/10，也可以用0.7来表示。把1米平均分成10份，其中的7份是7/10米，还可以用0.7米来表示，也就是7分米。把1元平均分成10份，其中的7份是7/10元，还可以用0.7元来表示，也就是7角。但是，如果是0.7时，那就是把1小时平均分成10份，每份是6分钟，表示其中的7份，也就是6×7 = 42（分钟）。

生₃：我还是不能理解为什么0.7时≠7分钟。

生₄：这是因为米、分米之间的进率和元、角之间的进率都是10，而小时和分钟之间的进率是60。

师：对，带有单位的分数和小数进行转化时，厘清它们之间的进率是非常重要的。

师：在计算0.3平方米=（ ）平方分米时，淘气和笑笑发生了分歧。淘气认为，0.3米 = 3分米，所以0.3平方米 = 3平方分米。而笑笑则认为，0.3平方米=30平方分米，她的理由是：因为3平方米 = 300平方分米，所以0.3平方米 = 30平方分米。你认为谁说得对？

生₅：笑笑的结论是正确的。我们刚才已经达成了共识，带有单位的分数和小数的转化，要注意它们之间的进率。平方米和平方分米之间的进率是100，0.3平方米的含义是把1平方米平均分成10份，每份是10平方分米，表示其中的3份，那就是10×3=30（平方分米）。

师：我们在认识小数的意义时，是结合人民币单位和长度单位模型进行思考的，这是因为元、角、分和米、分米、厘米相邻单位之间的进率都是10，这和小数中“10个0.1等于1，10个0.01等于0.1”有相通之处。但是，延伸到时间单位、面积单位之中，由于相邻单位的进率不是10，这个时候我们需要根据小数的意义并结合单位之间的进率进行转化。

师：现在，同学们能够自主计算12克=（ ）千克吗？（填小数）

生₆：1千克=1000克，1克= 1/1000千克= 0.001千克，12克 = 12/1000 = 0.012千克。

师：对，克与千克之间的进率是1000，同学们在进行单位转化时要注意这一点。

教学中，在学生能够从人民币单位和长度单位模型以及格子图的视角理解小数意义的基础上，教师结合学生已有的知识储备，进一步提升学生的认识高度，将小数的意义拓展到时间单位、面积单位等。这不但使学生更好地理解了小数的意义，还引导学生对带单位的分数和小数之间的互相转化进行了辨析，可谓一举两得。

课程标准明确指出：“数学教学活动必须建立在学生认知发展水平和已有知识经验基础之上。”因此，教师要从学生已有的知识储备和生活经验出发，遵循学生的认知规律，通过激活、对接、丰富、拓展学生的经验，引导学生的思维缓慢爬坡、拾级而上，让学生亲身经历知识产生和发展的真实过程，获得深刻的数学理解，促进学生在思维和能力方面的进步和发展。

（责编 金 铃）