服务员休假的生产服务库存模型的稳态分析及最优生产策略

徐 浩, 岳德权

(燕山大学理学院，秦皇岛 066004)

0 引言

随着生产库存理论研究的不断深入，对于现实生活中一些复杂的服务现象需要我们建立更加完善的模型。将服务员休假和生产库存系统相结合，有效地分析系统中无库存情况下的服务员休假的生产库存模型，通过求解稳态概率研究服务员休假对库存管理的影响。

在排队库存系统文献中，已有许多学者考虑了服务员(服务台)的休假对库存管理的影响问题。Daniel 和Ramanarayanan[1]研究了(s,S)策略的库存系统，其中服务台只有在库存变为零时开始休假。他们假设在缺货期间或服务台休息期间到达的需求将丢失。假设需求、提前期和休假时间遵循一般分布。通过使用更新和卷积技术，他们获得了稳态转移概率的表达式。Narayanan 等[2]考虑了具有随机正服务时间的库存系统。客户按照Markovian 到达过程到达，服务时间和休假时间具有位相型分布。只要系统中没有客户等待或库存水平为零，服务台就会休假。他们利用了水平相依的拟生灭过程对系统进行了稳态分析。Sivakumar[3]分析了一个具有马尔可夫需求的连续盘点库存系统。顾客到达服从Poisson 过程，服务时间服从指数分布。只有当系统库存为零时，服务员立即进行休假。休假结束后，若库存为零则继续休假，且休假期间到达的顾客进入无限空间的等待池。在稳态情况下获得了库存水平和系统中顾客数的联合分布以及系统的一些稳态性能指标。Padmavathi 等[4]分析了单重休假和多重休假的排队库存模型。只有当库存为零时，服务台开始休假，若休假结束时，库存已经到达，则服务台结束休假，否则继续休假。并假设Poisson 到达，指数服务时间和指数前置时间。利用矩阵几何解法得到了两个休假模型下的Markov 链的平稳分布以及产品库存水平和服务队列长度的联合概率分布。Koroliuk 等[5]讨论了一个带有易腐特性，不耐烦客户和服务员休假的排队库存系统，在假设Poisson 到达，指数服务时间和指数前置时间的条件下，得到最佳库存管理策略。

Krishnamoorthy 和Narayanan[6]研究了基于(s,S)策略的带有随机服务时间的生产服务库存系统，建立了系统队长、库存水平、生产状态的三维马尔可夫链，分析了系统稳态下的各项性能指标。王童毅等[7]考虑了两种不同优先级顾客的不耐烦行为和服务能力可调节的情况。建立了系统的Markov 模型，给出了系统的稳态分布，获得了系统的重要性能指标与利润函数，同时设计搜索算法获得了系统的最优库存水平与最优服务能力控制阈值，并得出基本库存水平，额外服务能力，顾客到达速率对系统净利润的影响关系。王晓燕等[8]研究了具有不耐烦顾客的生产服务系统的建模与优化问题。生产设施生产两种产品，服务台基于两类顾客的不同需求提供不同的服务，其每类顾客需要的产品一一对应。通过建立生产两类产品的生产服务系统Markov 模型，给出了系统稳态分布的求解方法，以及系统的重要性能指标。Baek 和Moon[9]研究了M/M/1 生产库存系统。客户根据泊松过程到达系统，并且单个服务器为客户服务。考虑外部订货和内部生产两种补货策略。最后得到系统的稳态分布。

目前，虽然在生产服务库存上的关注和研究较多，但在生产库存系统中考虑休假的文献则相对较少。Viswanath 和Krishnamoorthy[10]研究了具有服务员休假的生产服务库存系统。当库存为零时或者系统无顾客时，服务台开始休假。假设每个产品的生产时间遵循马尔可夫生产过程，并且客户到达过程遵循马尔可夫到达过程。他们求出了系统的稳态分布和稳态性能指标。Yue 和Qin[11]研究了具有服务时间和生产假期的生产库存系统。一旦库存水平变为零，生产设备开始休假，假设所有到达的客户在库存为零时丢失。根据拟生灭过程理论得到了系统稳态平衡条件，最后给出了一些数值结果。

服务员休假在网购系统方面有明显的应用背景。例如在网购环境下，网购平台提供“加购物车–下单–付款”的流程则是服务员向顾客提供服务的过程，网购平台可视为服务员。以网购某一物品为背景，在库存非零时，其网络平台向顾客提供服务的过程是一直存在的，即服务员一直在工作。当在重大节日或网购节日，如“双十一”等，由于下单量大，导致库存减少到零，此时网购平台会显示“缺货中，补货申请”，即网购平台无法向顾客提供“加购物车–下单–付款”的流程，也就是说，此时的网络平台对于这类物品是处于休假状态，至补货到达才开始工作。

本文基于上述背景考虑了服务员休假策略，但却与文献[10–11]有所不同。文献[10]假定库存为零或系统中没有顾客时服务员开始休假，而文献[11]假定库存为零时生产设备休假，没有考虑服务员休假的问题。本文假定服务员在库存为零时开始休假，系统没有顾客时如果库存非零，服务员不休假。第1 节给出了模型的描述和假设。第2 节进行了稳态分析，得到了系统的稳态平衡条件和稳态概率分布。第3 节给出系统性能指标和费用函数的计算公式，并通过数值算例分析了系统参数对性能指标，最优策略及最优费用的影响。第4 节给出了本文的结论。

1 模型描述

本文考虑具有(s,S)生产策略的服务员休假的M/M/1 生产服务库存模型，模型描述如下。

顾客到达服从参数为λ的泊松过程，顾客到达系统后形成一个队列，且每一个顾客只有一个产品需求。系统只有一个服务员，其服务时间服从参数为µ的指数分布，服务规则为FCFS。

此系统采用的是(s,S)生产策略，即当系统的库存水平下降到s时，生产设备立即启动，并且每次只能生产一个产品，产品生产后立即进入仓库，直到库存水平达到最大值S时，才停止生产，其生产时间服从参数为η的指数分布。

系统中只有一个服务员，当系统库存为零时，服务员开始休假。当假期结束时，若系统中有库存，则服务员立即进入忙期，否则，若休假结束时系统中无库存，服务员继续休假。休假时间服从参数为θ的指数分布。若系统中的库存非零，服务员不休假。服务员休假期间到达的顾客将被拒绝，不能进入队列。假设需求到达过程，服务过程和生产过程是相互独立的。

2 系统稳态分析

在本节中，我们首先使用拟生灭过程(QBD)推导出上一节中描述的系统的稳态条件。然后，我们推导出系统稳态分布并计算系统的一些重要的性能指标。

2.1 状态过程

定义系统的状态过程为ψ={(N(t),C(t),I(t),J(t));t ≥0}，其中N(t)表示t时刻系统中的顾客数；C(t)表示t时刻的库存水平；I(t)表示t时刻服务员的休假状态，其中I(t) = 0 表示服务员休假，I(t) = 1 表示服务员在岗(不休假)；J(t)表示t时刻生产设备的工作状态，其中J(t)=1 表示生产设备正在生产，J(t)=0 表示生产设备未生产。

过程ψ={(N(t),C(t),I(t),J(t));t ≥0}的状态空间为

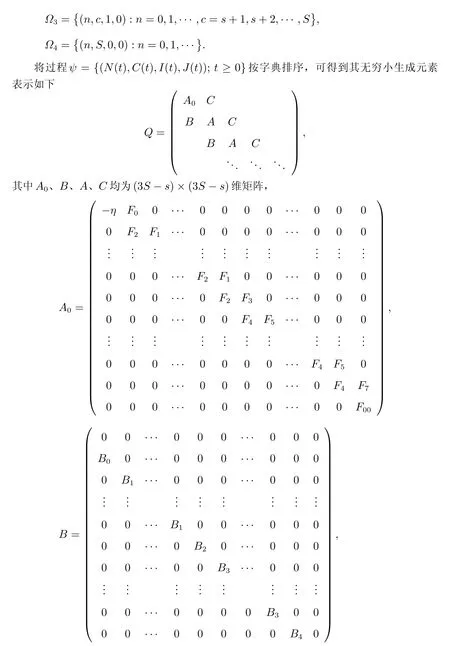
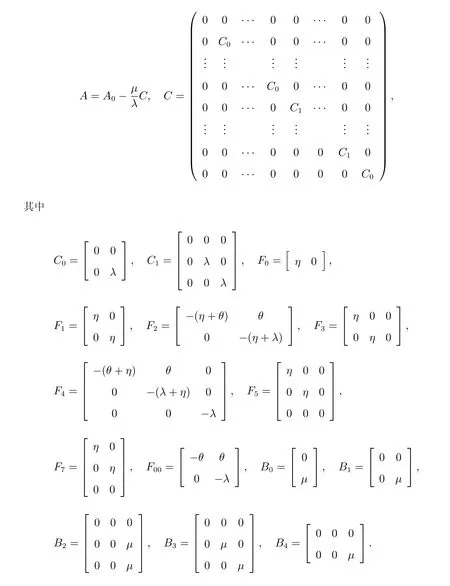
2.2 系统稳态平衡条件

由Q矩阵结构可知过程ψ={(N(t),C(t),I(t),J(t));t ≥0}是拟生灭过程。令M=C+B+A，则有

其中ζ表示服务员处于工作状态的概率之和，显然ζ ̸= 0。于是，系统稳态分布存在当且仅当λ<µ时成立。

2.3 系统稳态概率

首先考虑服务时间为零的情况，其中定义系统的状态过程为ˆψ={(C(t),I(t),J(t));t≥0}，其中C(t)、I(t)、J(t)的定义同2.1 节。

过程ˆψ={(C(t),I(t),J(t));t ≥0}的状态空间为

其中Pn是(3S −s)维行向量。

定理1 如果λ<µ，过程{X(t), t ≥0}的稳态概率为

3 系统稳态指标及费用分析

3.1 稳态指标

根据上述稳态概率向量的表达式，易求得系统稳态性能指标，具体如下所示。

1) 平均队长

上述公式中的π(S,0,0)由公式(19)给出，∆由公式(20)给出。

3.2 参数对性能指标的影响

1) 固定η=3, θ=2, s=5, S=45，考虑到达率λ对某些性能指标的影响。

由表1 可知，当到达率λ增大时，生产设备的平均生产率Erp，平均顾客损失率Eloss，服务员平均休假率Evac，生产设备生产时的系统平均库存Eon，平均生产启动率Epon都随之增大。不生产时平均库存Eoff和总平均库存Einv在减小。

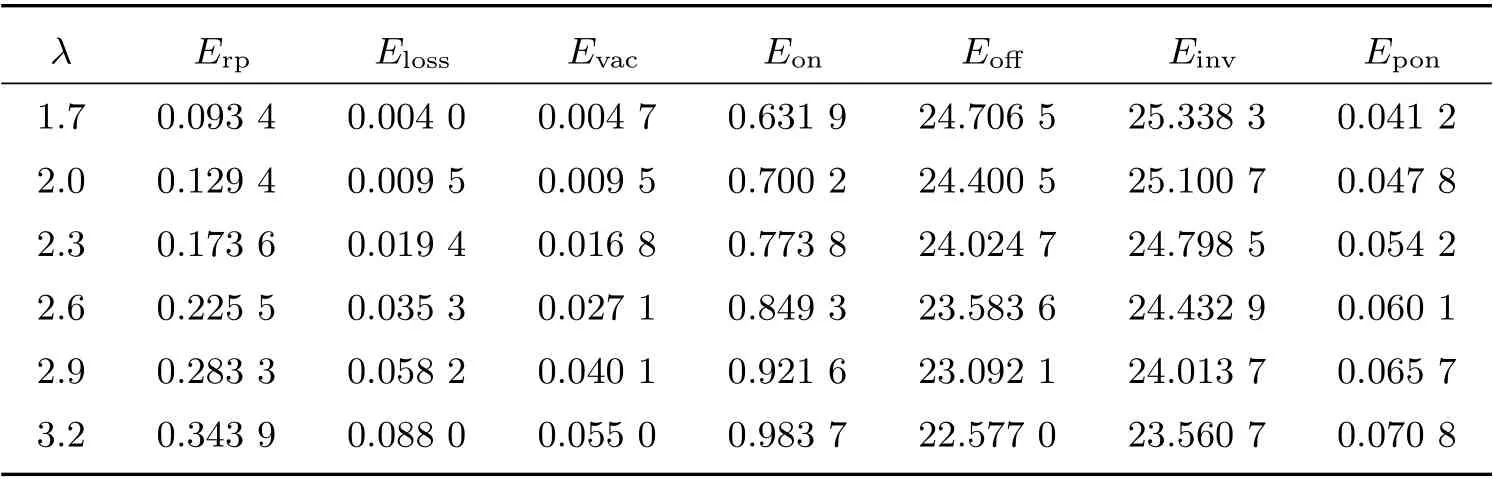
表1 参数λ 的敏感性分析

2) 固定λ=2.7, θ=2, s=5, S=45，考虑生产率η对某些性能指标的影响。

由表2 可知，当生产率η增大时，生产设备的平均生产率Erp，生产设备生产时的系统平均库存Eon，平均生产启动率Epon，不生产时平均库存Eoff和总平均库存Einv都随之增大。平均顾客损失率Eloss和服务员平均休假率Evac在减小。

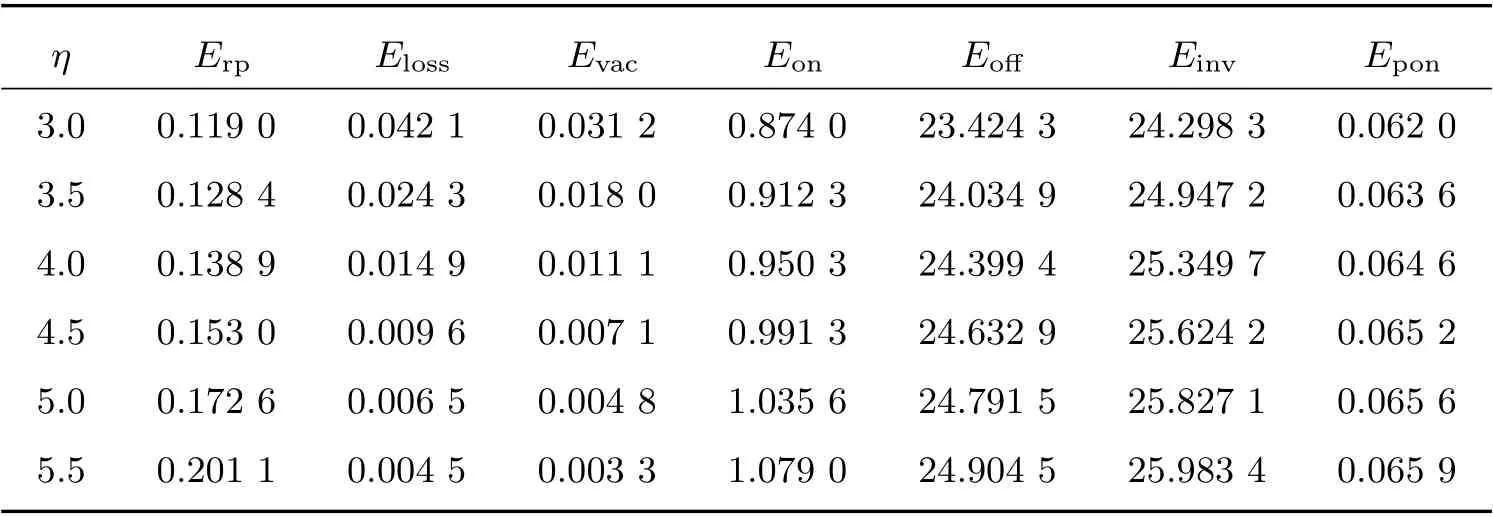
表2 参数η 的敏感性分析

3) 固定λ=2.7, η=3, s=5, S=45，考虑休假率θ对某些性能指标的影响。

由表3 可知，当休假率θ增大时，生产设备的平均生产率Erp和服务员平均休假率Evac都随之增大。平均顾客损失率Eloss，生产设备生产时的系统平均库存Eon，平均生产启动率Epon，不生产时平均库存Eoff和总平均库存Einv在减小。

表3 参数θ 的敏感性分析

3.3 费用分析

假设该库存系统的费用主要由服务费用、库存保管费用、生产费用、系统的顾客损失费用组成。令单位时间服务费用为Cs，单位时间单位库存的保管费用为Cinv，单位时间生产费用为Crp，单位时间顾客损失费用为Closs，生产启动费用Cpon，则系统费用函数为

本文引用王小平和曹立明[13]提出遗传算法(GA)对该库存系统的费用函数进行最优求解。遗传算法采用概率化的寻优方法，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向，因此大大加快了算法的收敛速度。

具体的算法步骤如下：

步骤1 初始化染色体，在可行性区域内随机生成含有M个体的初始群体；

步骤2 对决策变量进行整数约束，计算评价M个初始群体的适应度；

步骤3 进行个体交叉操作，进而判断个体的有效性。有效，则保留；无效，则进行随机位置交叉，直至生成有效的新的种群；

步骤4 进行个体变异操作，再次判断个体的有效性。有效，则保留；无效，则进行随机位置变异，直至生成有效的新的种群；

步骤5 对染色体个体进行选择操作；

步骤6 评价新群体的适应度，找到本代最好染色体，再与上一代进化最好染色体进行比较，记录每一代进化中做好的适应度和平均适应度；

步骤7 终止条件判断，如果当前选择满足终止条件则停止并输出当前选择为最优个体，否则转到步骤3。

现在，我们研究参数λ、η、θ、µ对最优策略(s∗,S∗)和最优费用函数C(s∗,S∗)的影响。数值结果由表4 至表7 给出。Cs=2, Cinv=1, Crp=20, Closs=50, Cpon=2。

表4 给出了参数λ取不同的值时，系统的最优控制策略和一些性能指标的取值变化，其中参数µ= 3.5, θ= 0.8, η= 3.5。由表4 可知，随着到达率λ的增大，其最小库存量在逐步减小，最大库存量在逐步增大，最优费用也在逐渐增大。

表4 参数λ 对最优策略和最优费用的影响

表5 给出了参数η取不同的值时，系统的最优控制策略和一些性能指标的取值变化，其中参数µ= 3.5, θ= 0.8, λ= 1.9。由表5 可知，随着生产率η的增大，其最小库存量在逐步增大，最大库存量在逐步降低，最优费用也在逐渐降低。

表5 参数η 对最优策略和最优费用的影响

表6 给出了参数µ取不同的值时，系统的最优控制策略和一些性能指标的取值变化，其中参数λ= 1.9, η= 3.5, θ= 0.8。由表6 可知，随着服务率µ的增大，其最小库存量无显著变化，最大库存量也无显著变化，而最优费用在逐渐降低。

表6 参数µ对最优策略和最优费用的影响

表7 给出了参数θ取不同的值时，系统的最优控制策略和一些性能指标的取值变化，其中参数λ= 1.9, η= 3.5, µ= 3.5。由表7 可知，随着休假率θ的增大，其最小库存量逐渐降低，最大库存量也逐渐降低，而最优费用在逐渐降低。

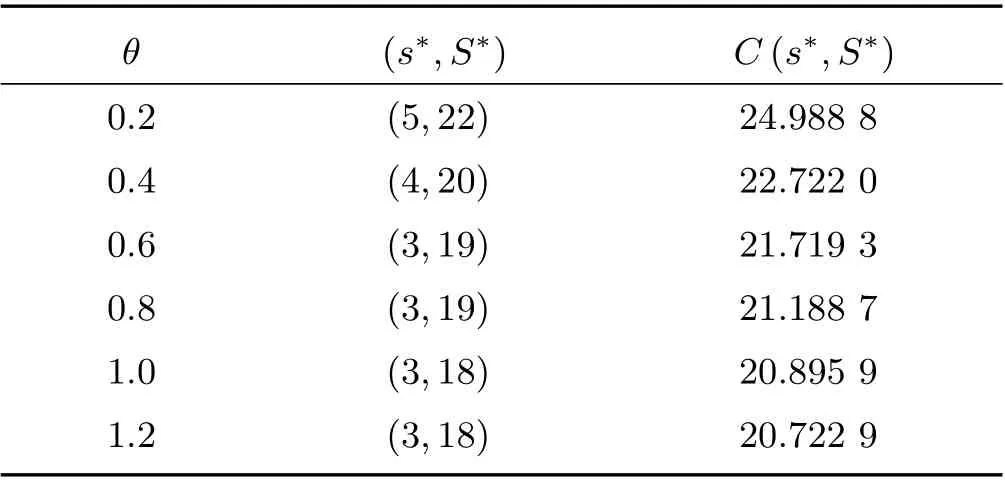
表7 参数θ 对最优策略和最优费用的影响

4 结论

本文研究了库存为零时服务员休假的M/M/1 生产服务库存系统，其中生产设施采用(s,S)策略。通过求解矩阵方程获得了系统队长和库存水平的联合分布，证明了系统的稳态概率分布具有乘积形式解。我们基于一些性能指标构建了费用函数。通过数值实验考察了一些参数对于性能指标和费用函数的影响。