预应力双柱式摇摆墩结构体系摇摆谱分析
2022-05-30王宝夫石祥锋张红芬
王宝夫, 石 钰, 石祥锋, 张红芬
(1.华北科技学院 建筑工程学院,北京 101601;2.北京工业大学 城市与工程安全减灾教育部重点实验室,北京 100124;3.中国建筑材料科学研究总院有限公司,北京 100024)
近年来,随着“震后功能可恢复桥梁”理念的兴起,摇摆桥墩受到学者们越来越多的关注[1-3]。摇摆桥墩将墩柱与盖梁及承台间的约束放松,地震作用下桥墩产生摇摆反应,依靠结构自重及无黏结预应力筋提供自复位能力,可有效减轻混凝土桥墩的损伤,显著降低桥墩的残余位移,具有损伤可控、震后可快速恢复的特点,成为一种新兴的桥梁结构抗震体系[4]。
利用摇摆减轻结构地震反应并不是一个新的概念,公元前510年建成的希腊神庙是现存最早的摇摆结构[5],该建筑在2 500年间经历多次大地震而未倒塌,表明摇摆结构具有良好的抗震性能。然而摇摆结构在当时并未受到人们的重视,直到1963年Housner[6]首先对刚体摇摆的动力反应进行研究,并提出了刚体摇摆的倒摆分析模型,揭示了刚体摇摆行为的尺寸-频率效应。此后学者们对刚体摇摆的动力行为进行了深入的研究,并扩展到摇摆框架[7-8]、摇摆桥墩[9-10]和三维摇摆结构[11-12]等结构体系。目前摇摆结构在桥梁工程中的应用还很少,现有文献报道中仅有新西兰的South Rangitikei桥[13]、Wigram-Magdala Link桥[14]以及我国的黄徐路桥。
Mander等[15]基于摇摆结构提出了混凝土桥墩免损伤设计理念,将桥墩与上部盖梁和下部承台分离形成摇摆界面,利用无黏结预应力筋提高桥墩的侧向刚度和自复位能力,摇摆桥墩的力-位移滞回关系呈S形,无黏结预应力筋的配置使得墩柱的摇摆刚度由负值变为正值。随后Cheng[16]对摇摆桥墩的地震反应进行了振动台试验研究,分析了不同参数对摇摆桥墩地震反应的影响,试验结果表明摇摆桥墩的漂移率可达6%,震后摇摆墩无损伤和残余位移;但未对预应力筋引起墩柱摇摆刚度的变化及对摇摆桥墩地震反应的影响进行分析。Zhou等[17]对双柱式摇摆桥墩的地震反应和减震效果进行了试验研究,试验桥墩呈现负摇摆刚度,振动台试验结果表明,合理配置预应力筋能够提高摇摆桥墩的抗倒塌能力,同时不显著降低摇摆墩的减震效果。
为提高摇摆墩的抗震性能,学者们提出了无黏结预应力技术与耗能部件联合应用的摇摆桥墩,并进行了一系列的试验和理论研究。Palermo等[18]在摇摆接缝处设置耗能钢筋以提高摇摆墩的耗能能力,并分析了初始预加力及预应力筋配筋率对摇摆墩抗震性能的影响。Marriott等[19]提出用外置耗能装置代替内置耗能钢筋以提高耗能装置震后的可更换性。Kam等[20]对不同类型耗能装置(滞回耗能、黏滞耗能)联合使用的影响进行了研究。这些研究结果表明,摇摆桥墩不仅具有良好的自复位能力,且具有较高的耗能能力,并可有效的减轻墩柱混凝土的损伤。需要说明的是上述研究中摇摆桥墩的摇摆刚度均为正值,其抗震性能介于纯摇摆桥墩和延性桥墩之间。
关于摇摆墩抗震性能的研究已取得一些成果,但主要集中在摇摆刚度为正值的情况,对摇摆刚度由负值过渡到正值的研究则较少。本文以双柱式摇摆桥墩结构体系为研究对象,如图1所示。考虑无黏结预应力筋对摇摆刚度的影响,基于拉格朗日方程和动量矩守恒定理给出预应力双柱式摇摆墩的刚体动力分析模型,并进行脉冲型地震动作用下的摇摆谱分析,讨论了预应力筋的影响,比较了不同的摇摆墩设计策略,为预应力双柱式摇摆墩的抗震设计提供依据。
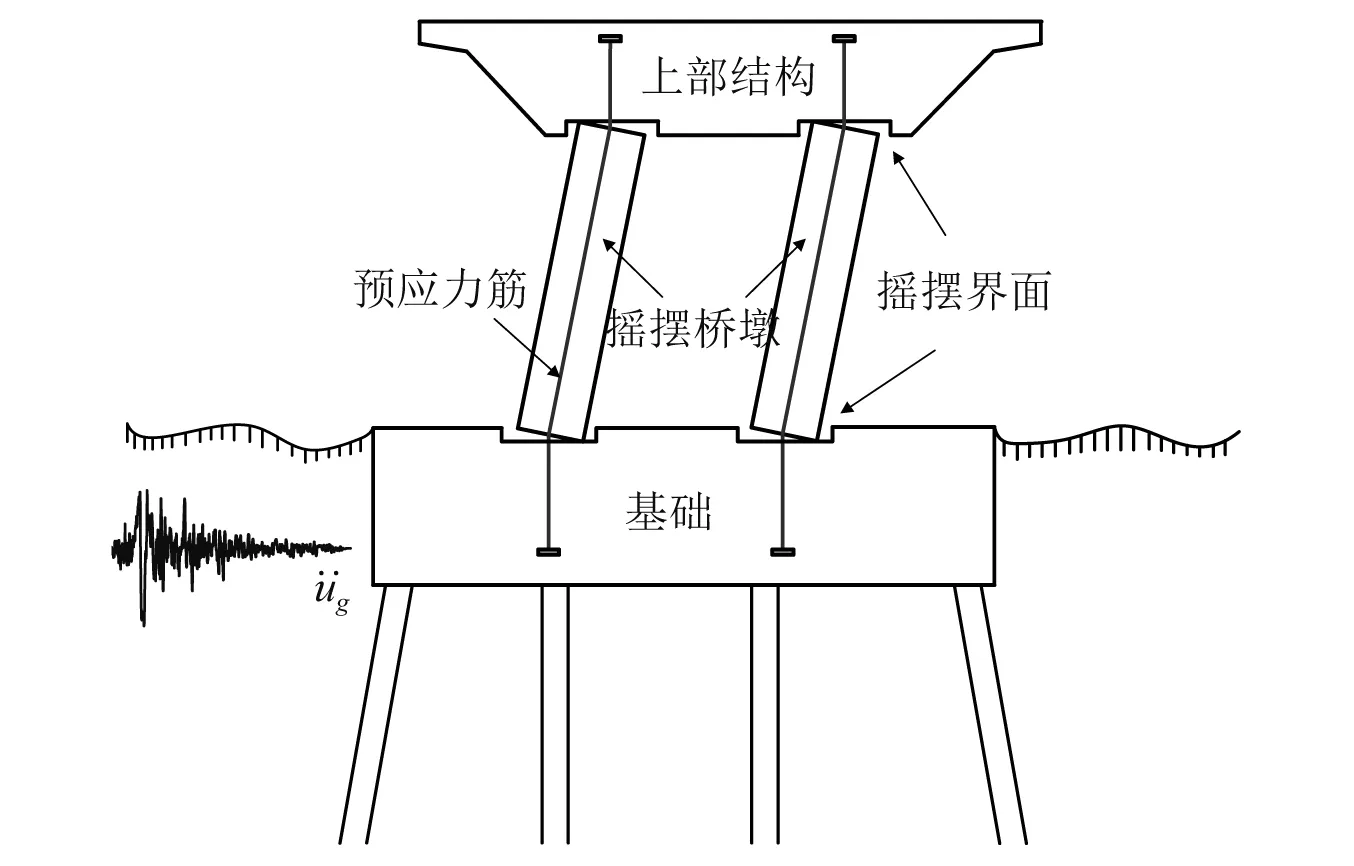
图1 预应力双柱式摇摆墩结构体系Fig.1 Posttensioned rocking double-column bridge system
1 分析模型
1.1 运动学方程
本节针对预应力双柱式摇摆墩的平面刚体摇摆反应进行研究,振动台试验表明通过合理的构造措施能够避免摇摆界面滑移和空间摇摆的出现,桥墩的摇摆反应可以限定在设计平面内。预应力双柱式摇摆桥墩横桥向刚体运动模式,如图2所示。从图2可知,地震作用下预应力双柱式摇摆桥墩产生顺时针(桥墩转角θ≻0)和逆时针(桥墩转角θ0)摇摆,桥墩与主梁和承台之间发生碰撞,碰撞后桥墩转角反向且桥墩绕新的脚点摇摆。

图2 预应力双柱式摇摆墩结构体系刚体运动Fig.2 Rigid motion of posttensioned rocking double-column bridge system
在桥墩摇摆时,上部结构为平面刚体运动,其水平位移u和竖向位移v可根据图2的几何关系由桥墩的转角θ表示
u=∓2R[sinα-sin(α±θ)]
(1)
v=2R[cos(α±θ)-cosα]
(2)
式中:顶部符号对应桥墩转角θ0;底部符号对应桥墩转角θ≻0;R为桥墩尺寸参数,其值为桥墩对角线长度的一半;α为桥墩的长细比,其值为墩高和对角线的夹角。
预应力双柱式摇摆桥墩可简化为以桥墩转角θ为广义坐标的单自由度体系,桥墩摇摆过程中需满足Lagrange方程,即
(3)
式中:T为体系的动能;V为体系的势能;Q为对应于广义坐标θ的广义力。
忽略预应力筋质量的影响,预应力双柱式摇摆桥墩体系的动能T可表示为
(4)
式中:nc为桥墩的数量;Io为桥墩相对于脚点O(O′)的质量惯性矩,桥墩为矩形截面时Io=4mcR2/3,mc为单个桥墩的质量;mb为主梁的质量。
预应力双柱式摇摆桥墩的势能可表示为
V=Vfr+Vt
(5)
式中:Vfr为体系重力提供的势能;Vt为无黏结预应力筋提供的势能。Vfr可采用式(6)表达
(6)
桥墩开始摇摆前,在初始预加力P0的作用下预应力束产生初始伸长量(Δp0)
(7)
式中,kt=EA/l为预应力筋的弹性抗拉刚度,E为钢束的弹性模量,A为钢束的截面面积,l为预应力束的无黏结长度。桥墩摇摆时预应力束产生变形(如图3所示),预应力束的伸长量为其底部和顶部伸长量之和
Δp=4bsin(θ/2)
(8)
则由预应力束提供的势能Vt可表示为
(9)

图3 预应力双柱式摇摆墩结构体系桥墩-基础连接Fig.3 Pier-foundation connection of posttensioned rocking double-column bridge system
预应力双柱式摇摆桥墩地震作用下的虚功δW可表示为
(10)
预应力双柱式摇摆桥墩对应于广义坐标θ的广义力Q为
(11)

式(12)可以简化为
(13)

(14)
(15)
1.2 初始摇摆加速度
对于预应力双柱式摇摆桥墩结构体系在任意虚位移δθ下运用虚功原理可得
(16)
式中:P=4ktbsin(θ/2)为预应力束伸长引起的预加力;δΔp为预应力束的虚伸长量可表示为
(17)
不失一般性,假定桥墩转角为正,将式(17)代入式(16)可得
(18)
当桥墩初始摇摆时,θ≈0,Δp≈0,式两边同除以ncmc可简化为
(19)

(20)
式(20)为随着初始预应力的增加桥墩的最小水平摇摆加速度也增大。
1.3 桥墩转角恢复系数
预应力双柱式摇摆桥墩的弯矩-转角曲线如图4所示,无量纲参数ρt和ρt0决定曲线的形状,曲线未包裹任何面积,体系无滞回耗能。当桥墩摇摆方向变号时,桥墩与上部结构和承台发生碰撞,体系的动能减小。假定碰撞的瞬时桥墩能够平稳转动,碰撞力集中在新的脚点处。在碰撞时(θ=0)预应力束的伸长量为零,碰撞前后预应力束不引起角动量的变化。因此,预应力双柱式摇摆桥墩结构体系的桥墩转角恢复系数同无预应力束双柱式摇摆桥墩的计算方法相同。周雨龙等基于碰撞前后的角动量守恒定律给出了无预应力双柱式摇摆桥墩的转角恢复系数
(21)
本文采用式(21)计算预应力双柱式摇摆桥墩结构体系的桥墩转角恢复系数。利用MATLAB程序进行运动方程[式(13)、式(20)和式(21)]的求解,得到预应力双柱式摇摆桥墩地震作用下的时程反应。
2 桥墩弯矩-转角关系

(22)
(23)
预应力双柱式摇摆桥墩体系的弯矩-转角关系曲线由无量纲参数ρt和ρt0控制,体系的恢复力矩MR为
4ρtsinθ+2sinαρt 0cos(θ/2)
(24)
当桥墩摇摆转角较小(cosθ≈1,sinθ≈θ)、桥墩长细比较大(cosα≈1,sinα≈α)时,体系的恢复力矩MR可简化为与桥墩转角θ线性相关的函数
(25)
预应力双柱式摇摆桥墩结构体系的弯矩-转角曲线,如图4所示。由图4可知,预应力双柱式摇摆桥墩结构体系的承载力随着预应力束无量纲初始预应力参数ρt0的增加而增大,其摇摆刚度随着预应束无量纲刚度参数ρt的增加而增大,并由负值逐渐转变为正值。由式(25)可知,在桥墩转角较小的前提下,预应力双柱式摇摆桥墩结构体系的摇摆刚度为正值的条件为
ρt≻0.25
(26)
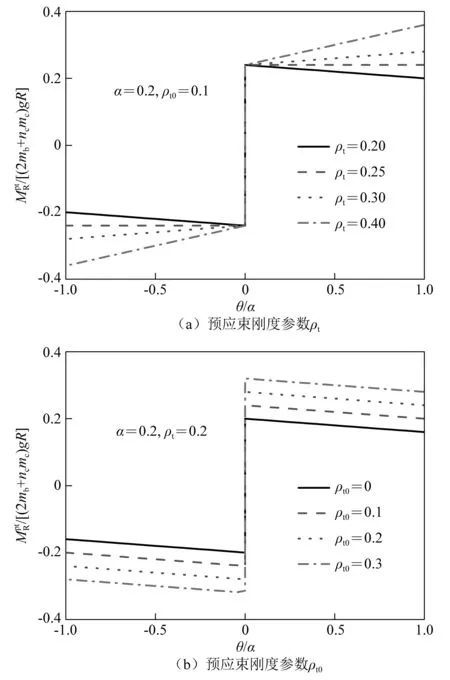
图4 预应力双柱式摇摆墩结构体系弯矩-转角曲线Fig.4 Moment-rotation curve of posttensioned rocking double-column bridge system
3 预应力双柱式摇摆墩摇摆谱
3.1 脉冲型地震动
摇摆结构体系在脉冲型地震动作用下容易发生倒塌[21],因此本节针对脉冲型地震动作用下预应力双柱式摇摆桥墩结构体系的摇摆谱进行研究。近断层脉冲型地震动具有较强的破坏性,但其运动形式相对简单,学者们对其进行了深入的研究并提出了多种数学模型来近似表征其运动学特征[22],这些数学模型能定性和定量的描述近断层地震动的脉冲特征。本文采用能够较好模拟近断层脉冲型地震动并被广泛应用于摇摆结构分析的Ricker小波[23]来进行摇摆谱分析,如图5所示。

图5 对称Ricker小波和非对称Ricker小波Fig.5 Analytical pulses: symmetric Ricker wavelet andantisymmetric Ricker wavelet
图5(a)为高斯分布e-t2二次导数的比例公式,即地震学中的对称Ricker小波,其表达式为
(27)
图5(b)为高斯分布e-t2三次导数的比例公式,即非对称Ricker小波,其表达式为
(28)
式中:Tp=2π/wp为Ricker波傅里叶谱的最大幅值对应的周期;β取1.380 1以使表达式的最大值等于ap。
3.2 共振频率
由式(25)可得预应力双柱式摇摆墩结构体系线性化的转动刚度
Kr=(2mb+ncmc)gR(4ρt-1)
(29)
当预应束无量纲刚度参数ρt>0.25时体系的转动刚度为正值,预应力双柱式摇摆墩结构体系的摇摆频率可表示为
(30)
式中,I0=4mR2/3为单个墩的质量惯性矩,上式可进一步简化为
(31)
当脉冲地震动的频率ωp=ωr时,预应力双柱式摇摆墩结构体发生共振
(32)
3.3 摇摆谱分析
对称Ricker小波作用下预应力双柱式摇摆墩结构体系的摇摆谱,如图6所示。结构体系的参数为α=0.2和γ=12。图中纵坐标和横坐标为相对于摇摆墩特征参数α和p的无量纲化坐标,加速度峰值从左向右分别为ap=0.405 4g(ap/gtanα=2)、ap=0.608 1g(ap/gtanα=3)和ap=0.810 8g(ap/gtanα=4)。从图6可知,当ωp/p较小时,即墩柱较小或长周期脉冲作用时,自由摇摆双柱式桥墩结构体系发生倒塌,摇摆刚度为正值的结构体系的摇摆谱存在峰值,峰值点频率可由式(32)计算得到,当ωp/p较大时,即墩柱较大或短周期脉冲作用时,预应力筋对双柱式摇摆墩结构体系的摇摆谱基本无影响。结构体系在非对称Ricker小波作用下的摇摆谱,如图7所示。从图7可知,其谱形与对称Ricker波作用下的摇摆谱具有相似的趋势。
以常规的公路双柱式桥墩为例来说明实际工程参数下结构体系的反应情况。第一种情况,双柱式低墩桥,桥墩墩高为7.5 m、截面尺寸为1.5 m×1.5 m,结构体系对应的参数为α=0.2,R=3.8 m和p=1.4。体系受到周期Tp=1.5 s的Ricker小波的作用,体系的无量纲频率参数ωp/p=2π/pTp=2.99。根据图6,当峰值加速度为0.405 4g时,无预应力自由摇摆墩的转角反应与预应力摇摆墩的转角反应相同,预应力刚度参数ρt对体系的反应基本无影响。当峰值加速度增加到0.608 1g,自由摇摆墩接近倒塌,预应力摇摆墩未发生倒塌,预应力刚度参数ρt较小(ρt=0.2)摇摆刚度为负值也能有效避免桥墩的倒塌。第二种情况,双柱式高敦桥,桥墩墩高为20 m、截面尺寸为4 m×4 m,结构体系对应的参数为α=0.2,R=10 m和p=0.84。体系受到周期Tp=1.5 s的Ricker小波的作用,体系的无量纲频率参数ωp/p=2π/pTp=4.98。由图6可知,在该Ricker小波的作用下自由摇摆和预应力摇摆体系均未发生倒塌,两者转角反应基本相同。基于以上分析可得,随着摇摆墩尺寸的增加,预应力对体系地震反应的影响减小。

图6 预应力双柱式摇摆墩结构体系对称Ricker波摇摆谱Fig.6 Rocking spectrum of posttensioned rocking double-column bridge system under symmetric Ricker wavelet
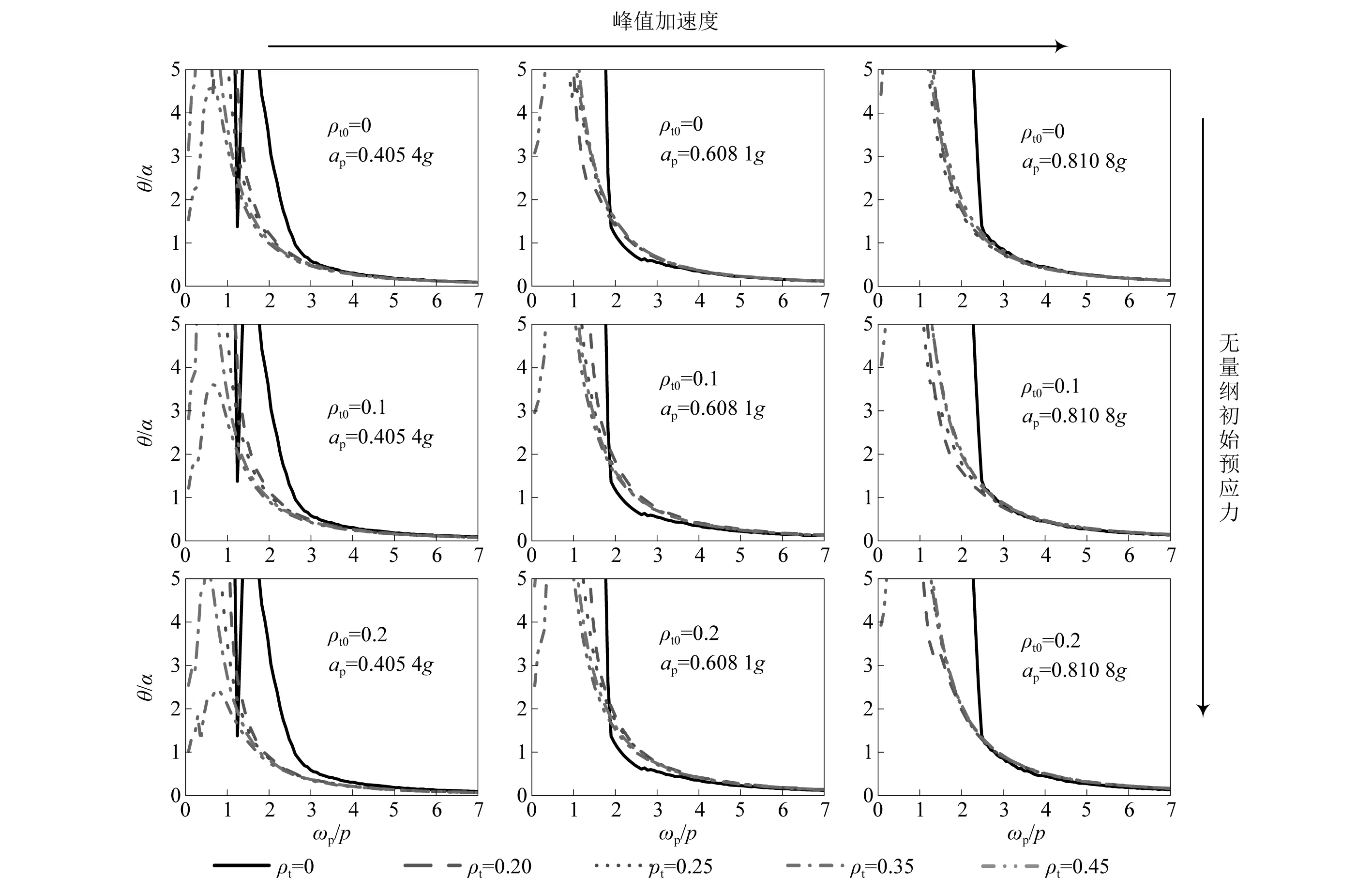
图7 预应力双柱式摇摆墩结构体系非对称Ricker波摇摆谱Fig.7 Rocking spectrum of posttensioned rocking double-column bridge system under antisymmetric Ricker wavelet
预应力双柱式摇摆墩结构体系在近断层地震动作用下的摇摆谱,如图8所示,选用的近断层地震动信息如表1所示。由图8可知,随着桥墩尺寸参数R的增大,结构体系的地震反应呈明显下降趋势,当R>5时,预应力筋刚度参数对结构体系的地震反应基本无影响。中等尺寸摇摆墩(4 表1 地震动信息Tab.1 The selected ground motions 图8 预应力双柱式摇摆墩结构体系摇摆谱Fig.8 Rocking spectrum of posttensioned rocking double-column bridge system 图9 预应力双柱式摇摆墩结构体系转角时程反应Fig.9 Rotation time history of posttensioned rocking double-column bridge system 本文以预应力双柱式摇摆墩结构体系为研究对象,基于平面刚体摇摆建立了该类预应力双柱式摇摆墩的刚体动力分析模型,进行了近断层脉冲型地震动作用下的摇摆谱分析,得出以下结论: (1)随着预应筋无量纲刚度参数ρt的增加,预应力双柱式摇摆墩结构体系的摇摆刚度逐渐增大,并由负值转变为正值。 (2)长周期脉冲地震动作用下或者桥墩为低墩时,增大预应力筋刚度可以减小桥墩的地震反应。随着桥墩高度或者脉冲地震动频率的增加,预应力筋刚度对桥墩地震反应的影响降低,此时预应力双柱式摇摆墩主要依靠桥墩自身的转动惯量抵抗地震作用。 (3)具有负摇摆刚度的预应力双柱式摇摆墩可以有效避免体系的倒塌,且墩柱脚点处也不会产生过大的局部压应力,可以减轻脚点处的局部损伤。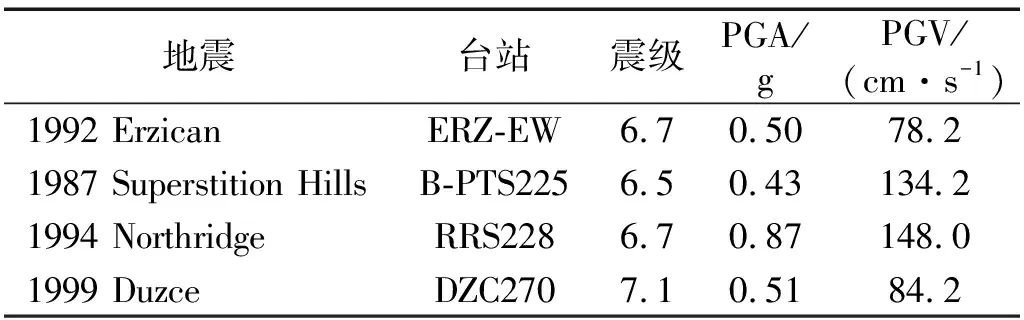


4 结 论
