装配式复合箍筋约束高强混凝土柱恢复力模型研究

2022-05-30李升才白巨巨朱永甫

振动与冲击 2022年10期

李升才，白巨巨，朱永甫

(1.莆田学院土木工程学院东南沿海工程结构防灾减灾福建省高校工程研究中心，福建莆田 351100;2.华侨大学土木工程学院, 福建厦门 361021；3.闽南理工学院绿色建筑施工与管理福建省高校工程研究中心，福建泉州 362700)

随着建筑工业化的快速发展，国内外学者[1-5]对采用灌浆套筒连接的装配式钢筋混凝土柱进行大量研究，但这些研究多集中于不同参数对其各项抗震指标的影响，而对其恢复力模型的研究甚少，目前在已出版的文献中，类似结构的现浇式柱的恢复力模型[6-8]早已提出，本文通过对比试验发现，两者在滞回特性和骨架曲线上存在特征差异，现浇式柱的恢复力模型不能很好的体现出装配式柱在循环往复荷载下的受力特点，因此有必要对装配式柱恢复力模型进行研究。

现阶段，国内外学者往往通过拟静力试验，对结构构件的试验结果进行简化和拟合，来研究其在特定条件下构件的滞回特性和恢复力模型，并取得一定的成果。刘阳等[9]对8个核心型钢混凝土柱进行循环往复加载试验，基于试验结果，建立了一种考虑配钢率和轴压比影响的恢复力模型。韦翠梅等[10]通过对钢-聚丙烯混杂纤维混凝土柱的试验数据进行拟合分析，提出相应的恢复力模型并与试验结果对比，两者高度吻合，证明了该模型的有效性。王德弘等[11]通过对活性粉末混凝土配筋柱的拟静力试验，采用理论计算与试验结果结合的方法，建立了恢复力模型，可为此类构件的抗震设计提供参考。于峰等[12]基于聚氯乙烯-碳纤维增强树脂(PVC-CFRP)钢管混凝土柱的试验研究成果，给出了柱骨架曲线特征参数计算式，并对试验结果进行回归分析，得到相应的恢复力模型。张建伟等[13]通过对HRB600级钢筋高强混凝土柱进行拟静力试验，深入研究了柱的抗震性能，并且在此基础上还建立了相应的恢复力模型。Yang等[14]以对再生骨料混凝土柱的拟静力试验为基础，给出了此种柱体的三折线恢复力模型，相应特征点计算方法可为工程应用提供理论依据。Lu等[15]借助他人研究成果，提出考虑包括含钢量等各种参数的钢骨混凝土柱的三折线恢复力模型，可为此种柱的非线性动力分析提供参考。Zhou等[16]根据12根碳纤维布加固钢筋混凝土圆柱在低周反复荷载作用下的试验结果，提出了一种三线恢复力模型，该模型可较准确预测地震作用下碳纤维加固柱的受力行为。这些研究表明不同的材性组合、结构构造、截面类型对柱体在低周往复荷载下的受力性能和破坏形态都有严重影响，进而导致相应的地震响应和滞回特性存在较大区别，所以在建立装配柱的恢复力模型时，应当考虑结构自身特点并进行分析。总的来说，对于普通混凝土柱、特种混凝土柱、型钢混凝土柱，以上研究所建立恢复力模型均采用三折线型，且与试验结果吻合较好，表明三折线模型具有较好的适用性。因此本文基于装配式复合箍筋约束高强混凝土柱拟静力试验结果，通过对其骨架曲线和滞回性能分析，在考虑轴压比和配箍率的情况下，给出了适用于装配式复合箍筋约束高强混凝土柱的三折线恢复力模型，以期为此种构件的工程应用提供参考。

1 试件概况

1.1 试件设计与制作

图1 试件构造及配箍方式(mm)Fig.1 The specimen structure and reinforcing form(mm)

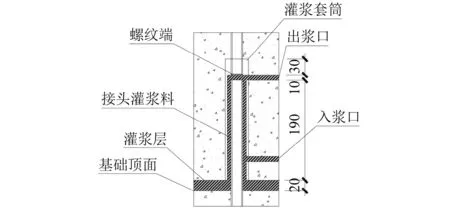
图2 连接处细部构造(mm)Fig.2 Detailed structure of the joint(mm)

表1 试验各试件参数Tab.1 Parameters of test specimens

1.2 材料力学性能

对试验所采用的HRB400钢筋，每种直径类型选取三根进行材性测试，测试结果取平均值。测量内容包括屈服强度fy，极限强度fb。具体结果如表2所示。套筒采用机械加工制作的半灌浆料GT22套筒，材料为优质碳素结构钢。对试验所配置C60混凝土和高强灌浆料进行标准立方体抗压试验，测得强度分别为66.5 MPa，63.4 MPa。

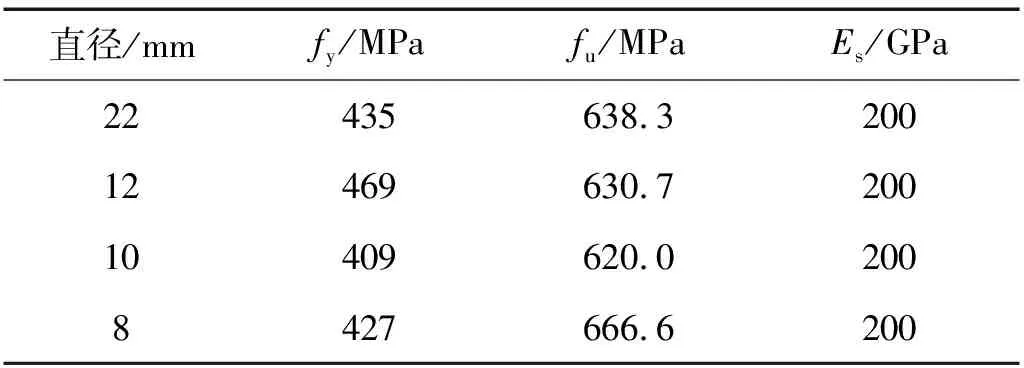
表2 钢材的力学性能Tab.2 Mechanical properties of steel

1.3 加载制度与加载设备

该试验采用MTS电液伺服加载试验机进行循环往复加载。由液压千斤顶施加竖向载荷并调整控制轴力，千斤顶的前端球铰在加载过程中可以自由旋转；MTS作动头施加相应的位移来控制水平荷载。试验设备如图3所示。根据JGJ/T 101—2015《建筑抗震试验方法规定》[17]的有关规定设计加载制度，如表3所示。试验初期，每级加载位移进行一次循环，待观察MTS显示屏实时绘制的荷载-位移曲线出现明显非线性变化时，此时可认为试件进入屈服状态，此后每级加载开始进行三次循环。当钢筋混凝土柱试件不能继续承担竖向荷载或试件的水平承载力下降到峰值荷载的85%以下时，试验停止加载。

图3 试验设备Fig.3 Test device

2 现浇式柱与装配式柱试验结果对比与分析

2.1 破坏现象对比

现浇柱(RCC-7)与装配柱(PRCC-3)在初期受力行为上并无明显差异，柱体第一条裂缝出现幅值均在1/250与1/150位移角加载之间，且位置均在柱脚底部100 mm范围。在进行1/100位移角三次循环过后，两者两则柱身均出现大量横向贯穿裂缝，且均匀分布于距柱底500 mm范围内。在位移角达到1/50时，虽然两者柱身原有裂缝都有不同程度的扩大，但装配柱与现浇柱开始表现出不同的破坏特征：装配柱柱底座浆层局部压碎开裂，在加载至最大幅值时，柱身与地梁出现轻微分离，如图4(a)所示，而现浇柱两侧柱底出现大量竖向裂缝，至加载结束，柱脚混凝土出现局部压碎，如图4(b)所示。当加载进行至1/35位移角循环时，装配柱出现异响，同时右侧柱底被严重抬起，承载力突降，这表明内部套筒内由于灌浆存在初始缺陷，钢筋被拔出，导致柱与地梁出现分离，如图4(c)所示，但左侧加载正常。现浇柱在此级循环下，柱底4个边角混凝土开裂压碎，并开始向两侧蔓延，至此级加载结束，柱底损伤严重，混凝土大面积脱落，如图4(d)所示。在1/20位移角加载循环结束时，装配柱柱底灌浆层严重碎裂，两侧柱底出现50 mm范围内保护层混凝土压碎脱落，如图4(e)所示。现浇柱柱底200 mm范围内破坏严重，混凝土大面积脱落，部分箍筋与纵筋外露，最终破坏如图4(f)所示。

2.2 骨架曲线对比

将各项试验参数均相同的试件PRCC-3和RCC-7试验数据整理并绘制骨架曲线，如图5所示。以此来分析套筒装配的构造形式对柱受力性能的影响。从图5可知，在弹性阶段，两者曲线几乎重合，表明装配柱与地梁之间黏结较好，柱底部套筒的存在并没有影响试件的前期刚度。

表3 加载制度Tab.3 Loading system

图4 破坏现象对比Fig.4 Failure phenomena comparison

图5 现浇柱与装配柱骨架曲线对比 Fig.5 Comparison of skeleton curve between cast-in-place column and prefabricated column

待试件达到屈服后，骨架曲线开始出现一定差异，此时观察到两试件正负方向曲线表现出的差异却有着显著不同，根据试验现象可知，装配柱正向加载一侧，部分套筒由于内部灌浆不密实等其他初始缺陷的存在，在达到峰值荷载时，套筒内钢筋被拔出，这使得后续加载正向侧混凝土受损程度大大加重，装配式柱骨架曲线在峰值荷载后承载力衰减速率变快，因此两者骨架曲线正向差异参考价值较小。本文着重分析负向骨架曲线来研究建造方式对柱受力性能的影响，试件屈服后，柱底部套筒所在区域形成一段刚度较大区域，造成塑性铰上移，且套筒存在一定程度上限制钢筋与混凝土之间的滑移，使得两者能够协同受力，导致同一加载位移下装配柱有着更高的承载力。又因为装配式柱整体性较弱，柱身与地梁在循环往复荷载作用下产生滑移，使得加载后期装配式柱承载力下降较快。

2.3 滞回曲线对比

试件PRCC-3和RCC-7的滞回曲线对比图，如图6所示。从图6可知，在加载前期，装配式柱与现浇式柱滞回曲线基本相同，当试件达到峰值荷载时，由于套筒的存在增大了装配柱底部局部刚度，导致装配式柱滞回环对角线斜率要大于现浇柱。随着加载的继续，装配式柱滞回曲线捏缩严重，分析试验现象可知在循环往复荷载作用下，装配柱的柱体与地梁的灌浆层破坏程度远高于柱身，灌浆层对柱底约束减弱，导致地梁与混凝土发生一定程度的滑移，致使加载后期装配柱滞回曲线的捏拢现象更严重。

3 骨架曲线

3.1 骨架曲线分析

整理试验数据，将各个装配柱的骨架曲线如图7所示。从图7可知，在整个加载过程中，可将曲线大致分为弹性阶段、强化阶段、强度退化阶段。

图6 现浇柱与装配柱滞回曲线对比 Fig.6 Comparison of hysteresis curve between cast-in-place column and prefabricated column

弹性段大致为试件开始加载至试件屈服，此阶段力随着加载位移的增大而快速提高，表现出较为明显的线性关系；试件屈服至峰值荷载为强化阶段，随着加载位移的增大，力增加速度有所放缓，开始呈非线性变化，刚度开始出现退化。试件达到峰值荷载后，进入破坏阶段，随着加载继续，试件强度开始出现衰减，刚度退化明显。且轴压比增大、配箍率减小时，曲线的下降段斜率也越大；骨架曲线反向加载力与荷载所体现出的变化趋势与正向基本相同。

综上所述，骨架曲线3个阶段表现出的力学特征，基本可以反映试件循环往复加载下的受力情况。轴压比和配箍率对骨架曲线的影响表现出明显的规律性，在建立骨架曲线模型时，为使结果更加准确可靠，应考虑此种影响。

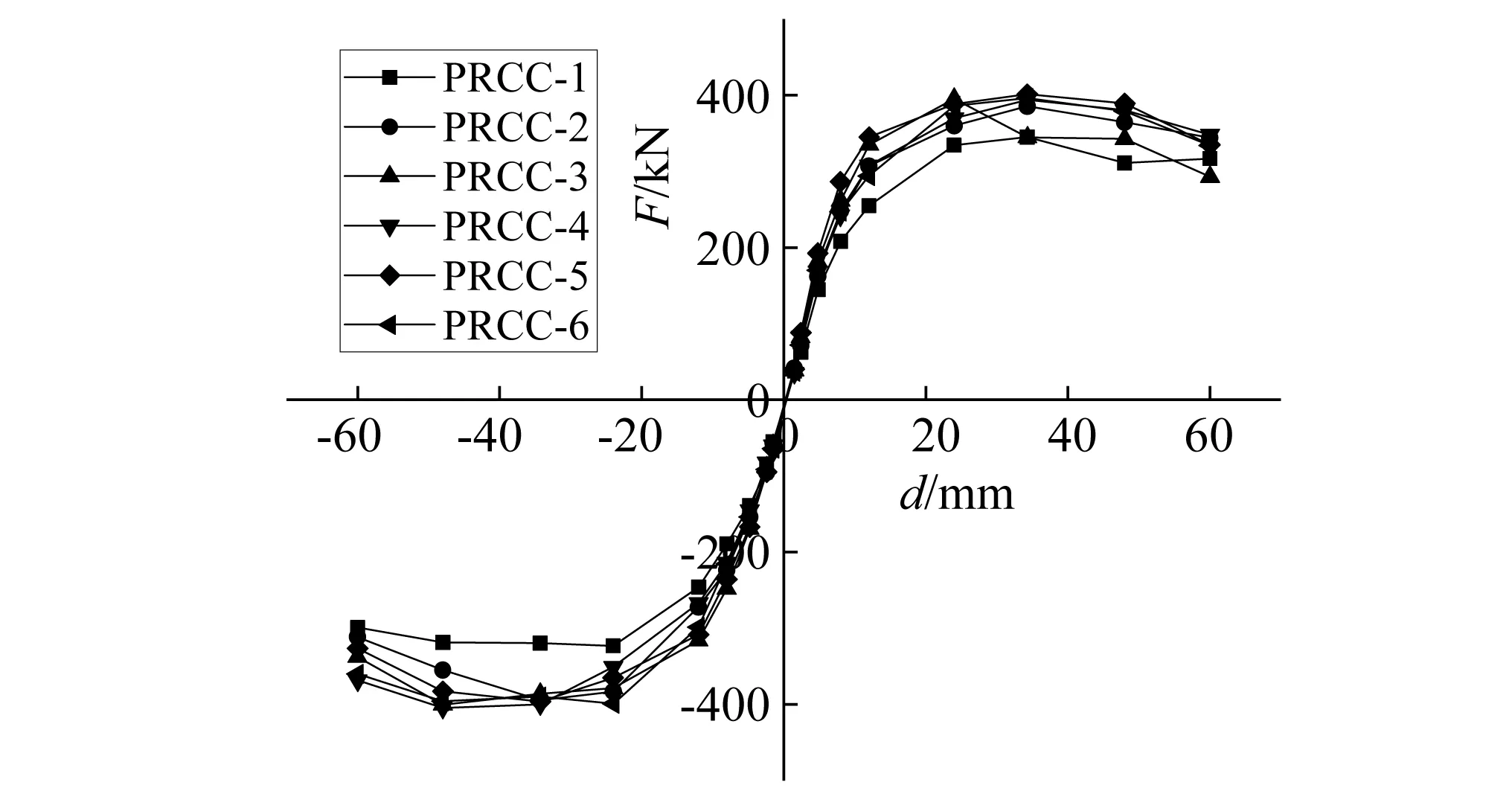
图7 各装配柱骨架曲线Fig.7 Skeleton curve of each prefabricated column

3.2 建议的骨架曲线模型

由前述分析可知，骨架曲线在加载过程中有较为明显的3个阶段，考虑到结构弹塑性反映分析及工程应用的方便，尽可能简化模型并结合闫长旺等[18-19]的研究方法，建立三折线骨架模型，如图8所示。

3.2.1 弹性阶段

试件加载至屈服时，虽然出现少量裂缝，但骨架曲线并没有出现明显拐点，卸载也几乎没有残余变形，故将此段简化为原点O至屈服点A的直线段，其斜率即为弹性刚度K1，加卸载均沿此直线进行。K1按式(1)计算

图8 骨架曲线模型Fig.8 Model of skeleton curves

K1=Fy/Δy

(1)

根据前述对比分析，现浇柱与装配柱在试件屈服前，两者受力情况较为相似，套筒的存在并没有影响试件早期的受力行为，因此对于屈服荷载Fy，屈服位移Δy的计算，同样可以采用现浇柱的截面分析法进行。在具体计算分析中考虑到材料特性、受力特点等因素，可做以下假定：截面平均应变符合平截面假定；受拉区混凝土不参与受力分析；混凝土受压区应力应变关系参考混凝土设计规范。同时考虑到箍筋对核心混凝土有一定约束作用，提高了混凝土抗压强度，故引入约束影响系数β。具体计算公式[20-21]如式(2)、式(3)、式(4)所示

(2)

(3)

(4)

式中：H为水平加载位置的高度；h0为柱截面有效高度；εy为纵筋屈服应变，根据材性测试结果，其值为60×10-4；ξy为试件屈服时截面的相对受压区高度系数；My为试件的屈服弯矩，分别可按式(5)、式(6)计算。

(5)

(6)

式中：ε0为混凝土轴心受压应变标准值；fc为混凝土轴心抗拉强度标准值。计算时以试验材性结果为基础，根据现行混凝土规范转化为对应的值；b，h分别为柱截面宽度和高度，fy为纵筋屈服应力，As为受压纵筋面积，ρsv为箍筋配筋率，fyv为箍筋屈服应力，a′s为柱保护层厚度。

通过计算发现，理论屈服荷载与试验结果相比偏低，分析可能的原因：根据计算可知，混凝土受压区相对高度系数均在0.35～0.44，可知构造钢筋在受力纵筋屈服时处于受拉状态，而在理论计算时，为简化计算，未考虑构造钢筋的受拉作用，同时柱底滑移变形的存在，也可能增大轴力所引起的弯矩，而计算中忽略这一影响。以上原因就导致理论屈服荷载偏低，故引入修正系数k来消除此种偶然误差，k为装配柱屈服荷载理论值与试验值的比值，计算取值为1.23。通过这种修正，可方便后续分析，且有效减少偶然误差的存在，能够更好地反映试件的恢复力特性。

3.2.2 强化阶段

试件屈服后，在往复荷载作用下，纵筋应变不断累积增大，混凝土裂缝拓展，导致试件总变形增大，承载力却增长缓慢。可将骨架曲线的屈服点A(Δy，Fy)与峰值点B(Δm，Fm)的连线作为强化段，其斜率K2为

(7)

在确定峰值点时，若采用理论计算，则需考虑试件变形(弯曲、滑移)、P-Δ二阶效应等因素，导致计算复杂，且结果误差较大。因此通过对试验结果的二元线性回归，来确定峰值位移与峰值荷载。在处理试验数据时发现试件峰值荷载和屈服荷载的比值大小，与轴压比、配箍率密切相关，因此可通过建立二元线性回归方程，来量化这2个参数的影响，其结果为

(8)

为了得到峰值位移与屈服位移的关系，同样的，以轴压比、配箍率为参数对试验结果进行二元线性拟合,得到骨架曲线强化段在水平方向的投影长度(Δm-Δy)与屈服位Δy的关系,具体拟合结果为

(9)

3.2.3 承载力退化段

将骨架曲线峰值点B(Δm，Fm)与极限点C(Δu，Fu)连线的直线段，看做三折线骨架曲线模型中承载力退化段。通过分析试验结果发现，轴压比增大，配箍率减小时，骨架曲线下降速率越快。可将此段斜率定义为K3=αK1，α为刚度退化系数，与轴压比、配箍率有关。通过对试验结果拟合回归，结果为

α=0.573ne-0.343ρv-0.007

(10)

3.3 骨架曲线比较

计算骨架曲线特征值并与装配柱的试验结果进行对比，具体结果如表4所示,并将三折线骨架模型与试验骨架曲线比较，如图9所示。从表4和图9可知，本文所建立的三折线骨架曲线模型与试验结果较为吻合，说明该模型可以反映出轴压比、配箍率对骨架曲线变化趋势的影响。但也存在个别试件与结果相差较大，分析原因可能因为试件本身存在一定初始缺陷，使得到的试验结果在拟合回归时，离散于主要变化趋势之外，因此导致与计算所得结果存在一定误差。

4 恢复力模型

4.1 滞回曲线分析

滞回曲线可以反映结构在低周往复加载过程中的受力特性，也是研究恢复力模型的基础[22]。将装配柱各个试件的滞回曲线列出，如图10所示。分析可得出以下结论：

(1)从图10可知，在加载初期，试件尚处于弹性阶段，滞回曲线基本为线性变化，滞回环呈尖梭形，卸载后几乎没有残余应力，随着加载进行，试件进入屈服阶段，加卸载段开始偏离直线，曲线的斜率随着荷载的增大而减小；卸载后出现明显的恢复变形滞后现象，表明卸载刚度退化。

(2)从图10的PRCC-1、PRCC-2、PRCC-3可知，随着轴压比的升高，峰值荷载过后的强度衰减加快，加载刚度退化明显，卸载曲线向位移轴偏移；滞回环变差，产生严重捏拢，说明轴压比是影响构件滞回曲线的重要因素。

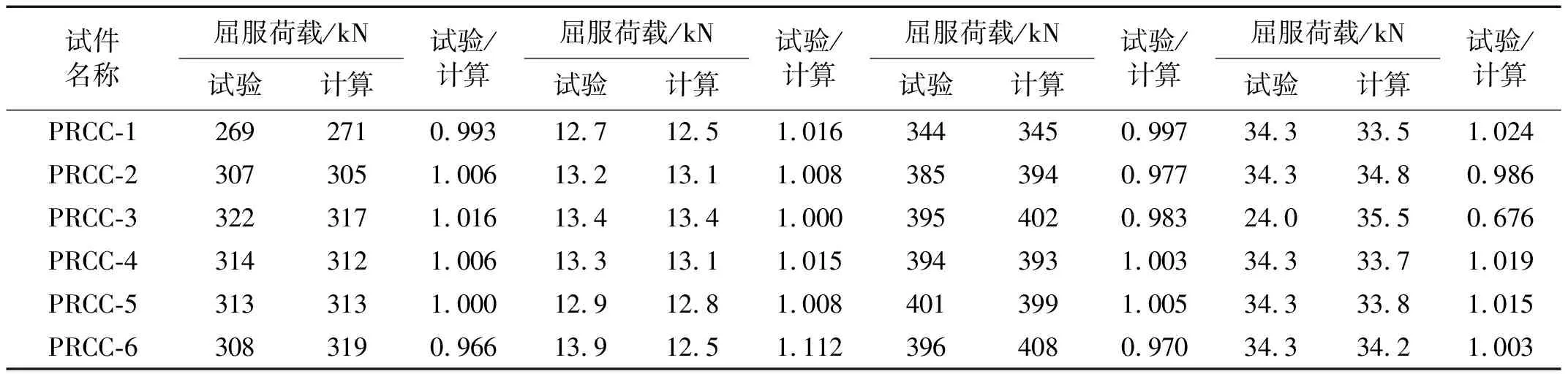
表4 骨架曲线特征点对比Tab.4 Comparison of characteristic points of skeleton curve

图9 骨架曲线对比Fig.9 Skeleton curve comparison

图10 各装配柱滞回曲线Fig.10 Hysteresis curve of each prefabricated column

(3)观察试件PRCC-3、PRCC-5与PRCC-3、PRCC-6可知，提高配箍率，试件承载力衰减速率降低，且可有效提高滞回环的饱满度，在同级循环位移下，滞回环对角线斜率较大，构件整体刚度有所提高。表明配箍率对装配式复合箍筋约束高强混凝土柱的滞回特性有着较为明显的影响。

4.2 卸载刚度

在试件屈服后，当加载至此位移幅值下最大位移点，同卸载曲线与位移轴交点的连线可简化为卸载段，其斜率为卸载刚度Ku。由上述分析可知：随着位移加载的增大，试件的卸载刚度存在明显退化。且在同一加载位移下，不同参数下的试件，其卸载刚度退化率不同。轴压比越大，柱底部在循环往复加载下弯曲破坏越严重，故试件卸载刚度退化率变大；而当配箍率增加时，由于对核心混凝土约束增强，减少柱体的损伤，因此其卸载刚度退化率变小。由表4可知，试件屈服大致位于第五、第六级加载位移幅值之间，为简化计算，将卸载位移Δu转换为与第五级加载幅值Δ5之比,其位移比定义为λ。在考虑轴压比、配箍率因素下，对试验结果进行拟合，得到装配柱的卸载刚度Ku与为常数的弹性刚度K1的关系为

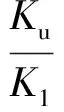
(11)

式中：a=-1.133ne+0.705ρv-0.046；b=-0.125ne+1.139ρv+0.019。

4.3 滞回规则

在得到关于装配式复合箍筋约束高强混凝土柱卸载刚度的拟合公式后，通过对滞回特性分析，在三折线骨架曲线模型基础上，提出恢复力模型的滞回规则。具体规则如图11所示。

图11 恢复力模型Fig.11 Restoring force model

(1)加载初期，试件处于弹性阶段，此时可认为加卸载刚度不发生变化，且卸载后无残余变形，加载路径均沿弹性段(OA和OA′)进行。

(2)随着加载的进行，试件进入强化阶段，此时加载路线沿AB进行，卸载时试件刚度发生退化，卸载路径由B点指向C点，卸载刚度可根据式(11)计算；反向加载时，若试件的水平荷载首次超过屈服荷载，则此时路径由正向卸载荷载为零的点C，直接指向屈服点A′，后沿着反向加载路径A′B′进行，在达到此位移幅值下的最大位移后卸载，卸载刚度与正向卸载刚度一致。

(3)再加载时则由负向卸载至荷载零点再次指向上一级位移幅值最大点(如C′B)，然后沿着正向骨架曲线强化段加载至本级位移幅值最大点后卸载，卸载刚度按式(11)计算。反向加载同正向一致，由正向卸载荷载零点指向负向的上一级位移最大处(如CB′)，后沿着负向骨架曲线强化段加载至本级负向最大位移处卸载。

(4)若上一级位移幅值等于或大于峰值荷载位移，则本次正向加载沿着骨架曲线下降段进行，滞回规则与强化段的规则相同。