小半径曲线中低速磁浮车辆-轨道耦合系统动力响应分析

2022-05-30王相平李国芳慕显龙王红兵靳忠渊丁旺才

振动与冲击 2022年10期

王相平，李国芳，慕显龙，王红兵，靳忠渊，丁旺才

(1. 兰州交通大学机电工程学院，兰州 730070； 2. 太原铁路局集团公司太原车辆段，太原 030012)

曲线线路是中低速磁浮交通主要的线路类型之一，当车辆通过小半径高架曲线线路时，车轨耦合振动以及车辆横向动力失稳问题将会愈加突出，严重影响车辆运行品质，甚至危及车辆运行安全[1]。

磁浮列车是一个集车辆系统、轨道系统、悬浮控制系统于一体的复杂大系统[2-5]。磁轨关系从本质上决定了磁浮列车的动力特性，曲线段上磁铁相对于轨道的运动关系更为复杂，且横向欠阻尼特性使中低速磁浮车辆横向动力失稳的潜在可能急剧增加。赵春发等[6]指出，低速EMS磁浮车辆没有专门的导向电磁铁，这将对车辆的动态曲线通过性能产生严峻考验，同时，二维磁轨关系也难以准确反映曲线线路上电磁铁相对于轨道的三维运动特性。近年来，电磁力-气隙模型[7]、基于虚拟位移法建立的三维电磁铁分析模型[8]、采用有限元法建立的线圈磁力分析模型[9]、单自由度广义Bouc-Wen磁滞模型[10]等逐渐被用于磁轨关系计算。控制系统在动态磁轨关系分析中也必不可少[11-13]。悬浮控制系统的稳定并不能保证磁浮列车的动力稳定，静悬或低速通过弹性高架桥梁时的车轨耦合振动给磁浮车辆的安全运营造成了严峻挑战[14]。Hu等[15]研究表明弹性桥梁低阶频率对车桥耦合振动影响较为显著；Zhou等[16]研究发现主梁扭转共振是车桥耦合振动的主要原因；王连春等[17]指出悬浮系统的有源功率是自激振动产生的主要原因；王党雄等[18]研究表明，桥梁结构变形引起悬浮间隙改变，影响电磁力，导致磁浮车桥耦合共振发生；Liang等[19]、李小珍等[20]、汪科任等[21]、Wang等[22]研究表明桥梁结构型式、轨道梁跨距、桥梁竖向挠跨比等均会对车桥耦合振动产生影响。

综上可知，当前有关曲线段磁浮车辆动力学的研究主要以大半径曲线上的高速车辆为主，中低速磁浮小半径曲线上的动力特性鲜有研究；中低速磁浮车辆磁轨动力学依旧以二维电磁力模型为主，空间三维动态磁轨关系尚未充分体现；轨道模型的精细化对车桥耦合系统动力学计算精度影响较大[23]，但当前研究基本只考虑了轨道梁的柔性，对与悬浮电磁铁直接作用的F轨、轨枕等关键部件的参振作用尚未考虑。

鉴于此，建立考虑F轨、钢轨枕、承轨台、轨道梁多层柔性体的精细化小半径曲线轨道模型；运用Ansys APDL-UM-Maxwell进行车辆-桥梁-电磁场全耦合仿真，模拟了小半径曲线上的空间动态磁轨关系；结合实测数据验证了模型的准确性，分析了钢构小半径曲线上中低速磁浮车辆-高架轨道系统的动力响应，研究结论以期为曲线段中低速磁浮高架轨道设计、车辆安全运营提供理论基础和技术保障。

1 数值计算模型

1.1 中低速磁浮车辆模型

车辆主要由车体、走行部和悬浮系统组成，走行部主要包括悬浮架、二次系与迫导向机构，每辆车有五个悬浮架均布于车下，每个悬浮架由抗侧滚梁将左右模块连接起来，整车模型共有154个自由度，车辆总体结构示意图如图1所示。

图1 车辆系统总体结构示意图Fig.1 Diagram of overall structure of vehicle system

迫导向机构示意图(见图1(e))。车辆通过曲线线路时，前端悬浮模块随轨道偏转，车体和悬浮架之间发生相对横移，带动长T型臂转动，长T型臂通过转向拉杆带动短T型臂转动，使第二悬浮架拟合曲线运动，第三悬浮架自由随动。

1.2 空间动态磁轨关系模型

当前广泛用于中低速磁浮车辆的电磁力模型大多是基于虚功法、保角变换法或磁通管法分解转化为单极电磁铁模型计算求解。当F轨与U型电磁铁极面正对且平行时，悬浮气隙磁场中的能量为

Wm=μ0H2AS

(1)

式中：μ0为真空磁导率；H为气隙内的磁场强度；A为磁极面积；S为气隙。

若忽略导磁介质内部磁阻，则

(2)

式中：N为电磁铁线圈匝数；I为通过线圈的电流。

依据虚功原理，则电磁力可表示为

(3)

进一步采用保角变换和四角几何法对电磁力进行分极计算，则悬浮力FZ和导向力FY可表示为

(4)

(5)

式中：wmag为磁极宽度；y为电磁铁相对横移量。

式(1)～式(5)有关电磁力的计算是在忽略磁阻并假定F轨与U型电磁铁极面正对且平行为基础的，而当车辆在曲线线路上运行时，线路曲率变化导致电磁铁纵向中心线与F轨纵向中心线不再平行，悬浮电磁铁相对F轨发生横摆、摇头、点头、浮沉运动，此时悬浮电磁铁与F轨的几何关系示意图，如图2所示。

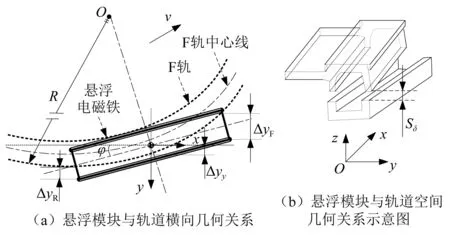
图2 平曲线上悬浮电磁铁与F轨几何关系示意图Fig.2 Diagram of the geometrical relationship between the suspension magnet and F rail on the horizontal curve

依据图2(a)所示几何关系，轨道曲率变化引起的悬浮电磁铁端部与F轨之间的横向错位可表示为

(6)

式中：R为曲线半径；Lmag为悬浮电磁铁长度。

记悬浮模块摇头角为φ，电磁铁质心相对于F轨中心线的横向偏移量为Δyy，则悬浮电磁铁首、尾两端的横移量为

(7)

(8)

每个悬浮电磁铁由四个线圈沿纵向排列封装而成，而每一处横移量均不相同。在图2(a)所示电磁铁坐标系xoy上，任一点A(lx,0)对应的横移量为

(9)

结合图2(b)，进一步考虑电磁铁相对于F轨的浮沉和点头运动，记考虑浮沉后的悬浮间隙为Sδ，点头角度为θm。将电磁铁沿长度方向离散，则点头运动在离散后的任意一点均可由该点悬浮间隙SδAi表示，基于此可将悬浮力和导向力表示为

(10)

(11)

悬浮力矩和导向力矩为

(12)

(13)

式中：lxi为离散点Ai(lxi,0)距电磁铁中心的纵向距离；SδAi， Δylxi为图2所示电磁铁坐标系内任一离散点Ai对应的悬浮间隙和横移量；fZAi(SδAi,Δylxi,I)，fYAi(SδAi,Δylxi,I)分别为Ai点处对应的悬浮力、导向力大小，其理论解为椭圆域内的积分，计算极为复杂，故综合考虑导磁介质的磁饱和效应，采用Maxwell对其进行计算。计算过程中，部分关键参数取值如表1所示。

表1 悬浮电磁铁部分关键计算参数Tab.1 Some key calculation parameters of suspension magnet

悬浮控制方式对车辆-轨道系统的动力响应具有较大影响，为减小控制策略对主要研究对象的影响，采用了当前广泛使用的PID(proportional integral derivative)控制方式。悬浮系统控制方程为

(14)

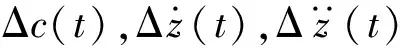
1.3 车辆-曲线段柔性高架轨道耦合系统模型

中低速磁浮车辆正线线路最小曲线半径为100 m，结合实际工程背景，建立跨度20 m半径R=100 m的某五跨连续梁钢构高架轨道模型。轨道材料Q235-B，建模过程中，F轨、钢轨枕、承轨台、轨道梁均采用solid185单元模拟，F轨与钢轨枕固结，钢轨枕与承轨台之间的扣件用bushing力元模拟，车辆与轨道之间依据磁轨关系耦合。轨距1.86 m，轨枕间距1.20 m，缓和曲线长54 m，线形为三次抛物线，圆曲线长18 m，曲线段前后均设置50 m直线线路，超高根据式(15)设置，最大超高处左右轨面与水平夹角小于6°,最大通过速度40 km/h。车辆-曲线段高架轨道耦合系统示意图如图3所示。

(15)

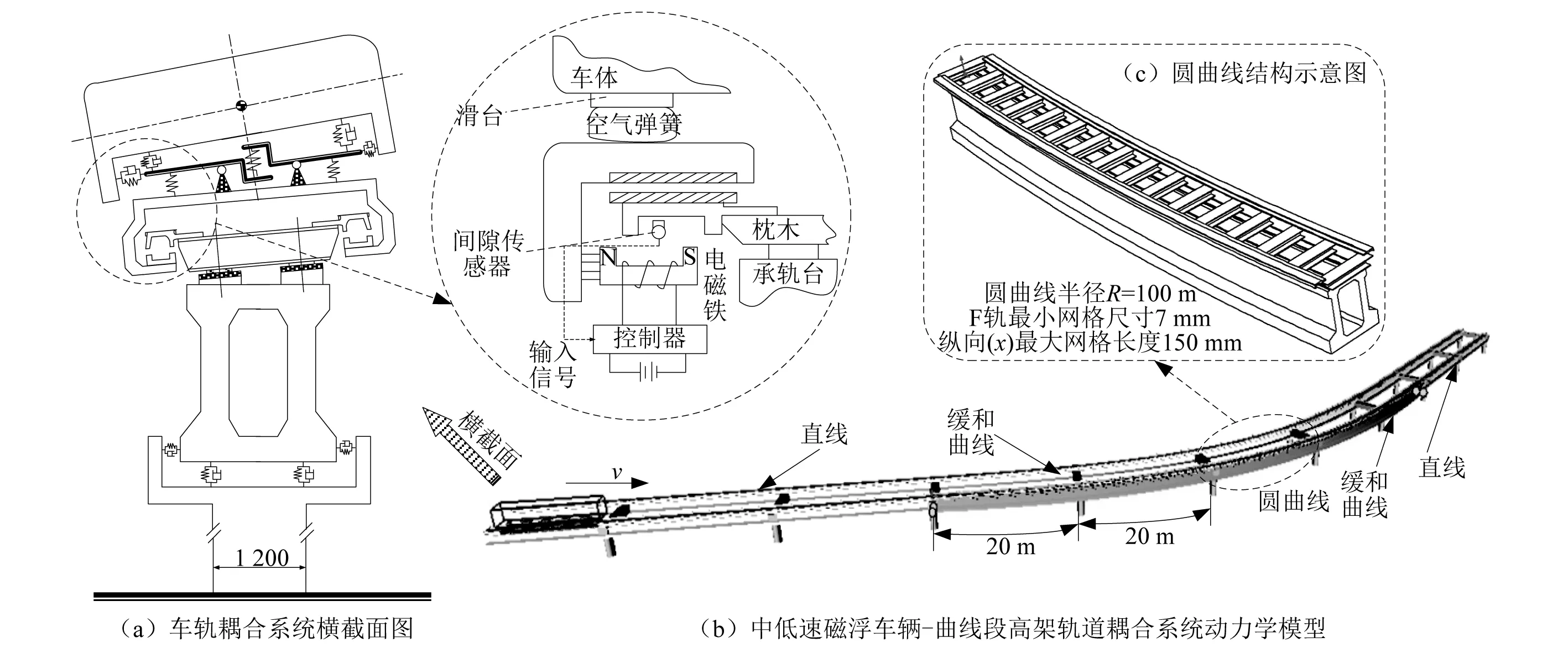
图3 中低速磁浮车辆-曲线段柔性高架轨道耦合系统示意图Fig.3 Schematic diagram of the coupling system of low-medium speed maglev vehicle-curved section flexible elevated track

由于当前中低速磁浮运营里程相对较短，轨道不平顺实测数据较少，故基于柔性高架线路随机不平顺谱理论，结合CJJ/T 262—2017《中低速磁浮交通设计规范》[24]中对轨道精度的要求，反演出轨道不平顺如图4所示。

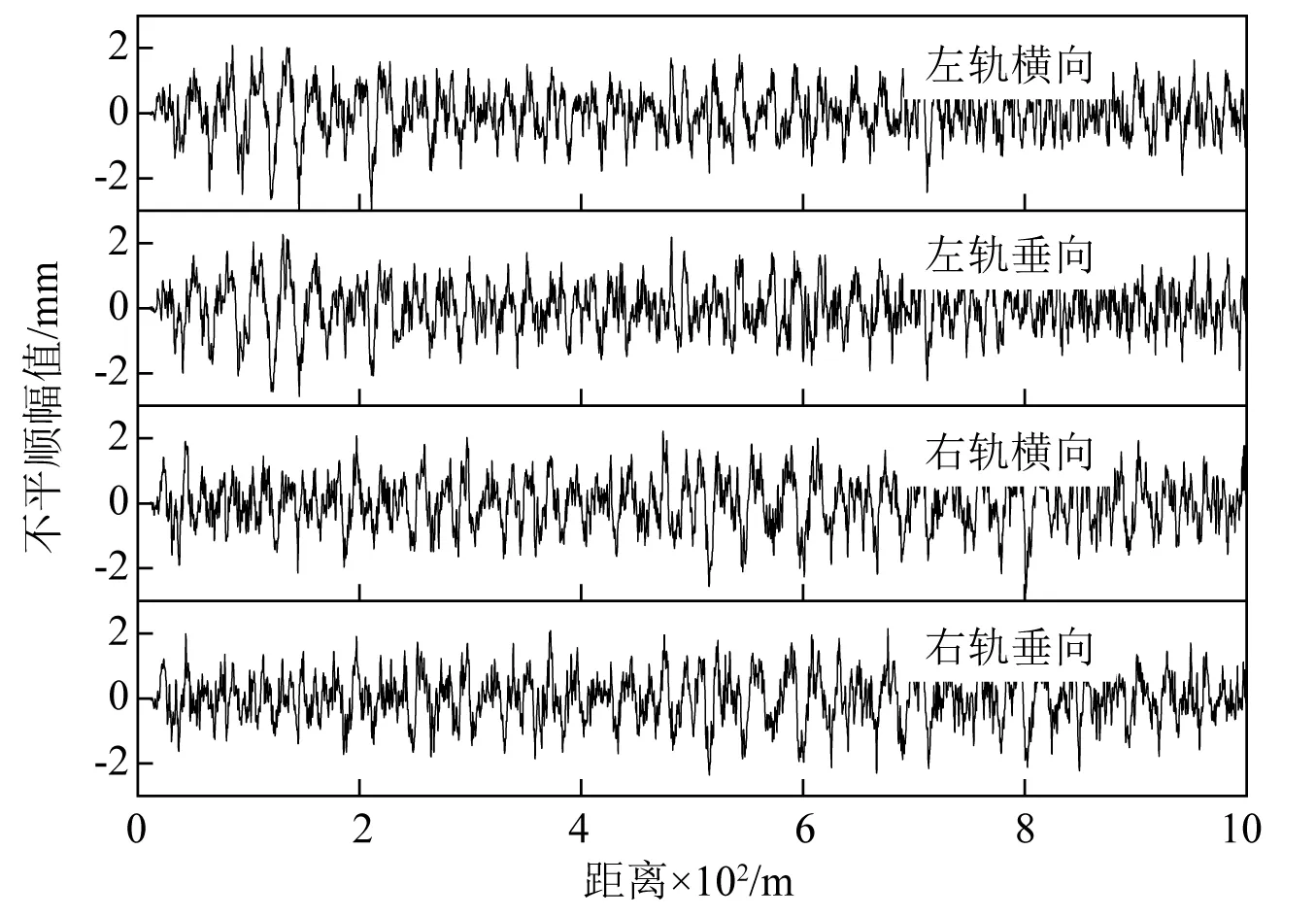
图4 轨道不平顺Fig.4 Track irregularity

计算流程如图5所示。

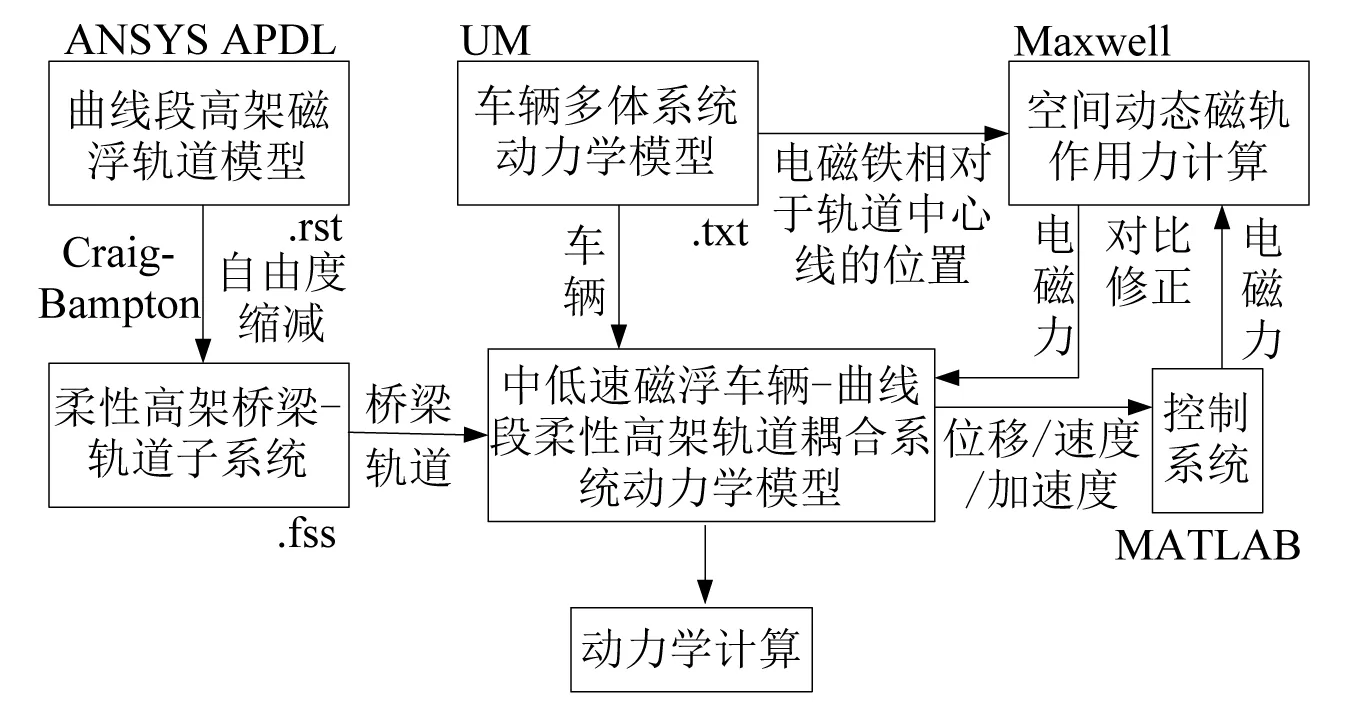
图5 车辆-桥梁-电磁场多场耦合计算流程Fig.5 Multi-field coupling calculation flow of vehicle-bridge-electromagnetic field

在动力学计算中，车辆系统动力学方程为

(16)

式中：MV，CV，KV为车辆系统质量、阻尼、刚度矩阵；XV，XC为车辆系统和控制系统状态矢量；Q为轨道梁广义位移矢量；FM为车辆系统外力矢量，考虑动态磁轨作用，其可表示为

FM=(fm1,fm2,…,fmn)

(17)

(18)

式中：ik为第k个线圈的电流；其余符号意义同上。

对轨道梁系统的求解采用模态叠加法，轨道系统动力学方程为

(19)

式中：qj为第j阶广义位移；ξj，ωj，φj为第j阶的阻尼、固有频率和振动模态；Fj为第j阶的广义力。

1.4 模型验证

1.4.1 电磁力

采用常用二维解析模型与本文计算结果的对比来验证电磁力模型的正确性。

选取左侧电磁铁，以车辆运行方向自前向后标记该电磁铁上四个线圈分别为LF1、LF2、LR1、LR2，由式(6)～式(9)，结合车辆多体动力学模型可计算得到曲线线路上电磁铁任意位置横向位移及悬浮间隙，再将计算结果代入式(4)和式(5)即可求得任意位置的电磁力。本文所用电磁力模型是在有限元仿真基础上采用数值拟合手段对电磁力进行表示。车辆20 km/h运行时，两者计算结果对比如图6所示。

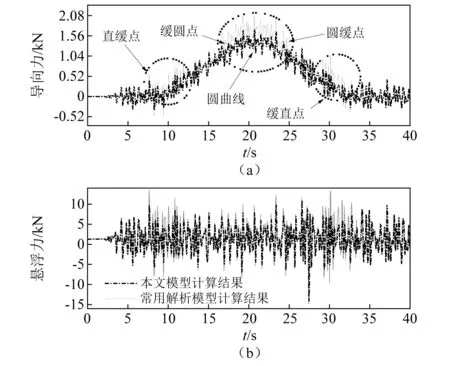
图6 线圈LF1处电磁力计算结果对比Fig.6 Comparison of electromagnetic force at coil LF1

由图6可知，两者计算结果变化趋势基本一致，但本文计算结果普遍小于解析解，在直缓点、缓圆点、圆缓点、缓直点等表现更为显著。这是因为有限元仿真过程中还进一步考虑了导磁介质中磁阻的变化，在轨道不平顺以及线路曲率等多重激励联合作用下，导磁介质工作点极易转移到磁饱和区，从而引起磁动势下降，故其对应数值解要小于不考虑磁阻的二维解析解。

1.4.2 车辆-高架轨道耦合系统

李小珍等对长沙中低速磁浮运营线中10～80 km/h运行速度下某连续梁中跨跨中动挠度进行了现场测量并进行了数据拟合，由于本文所选取曲线线路车辆最大可通过速度为40 km/h，故将其实测结果重新截取拟合后与本文计算结果进行对比，如图7所示。

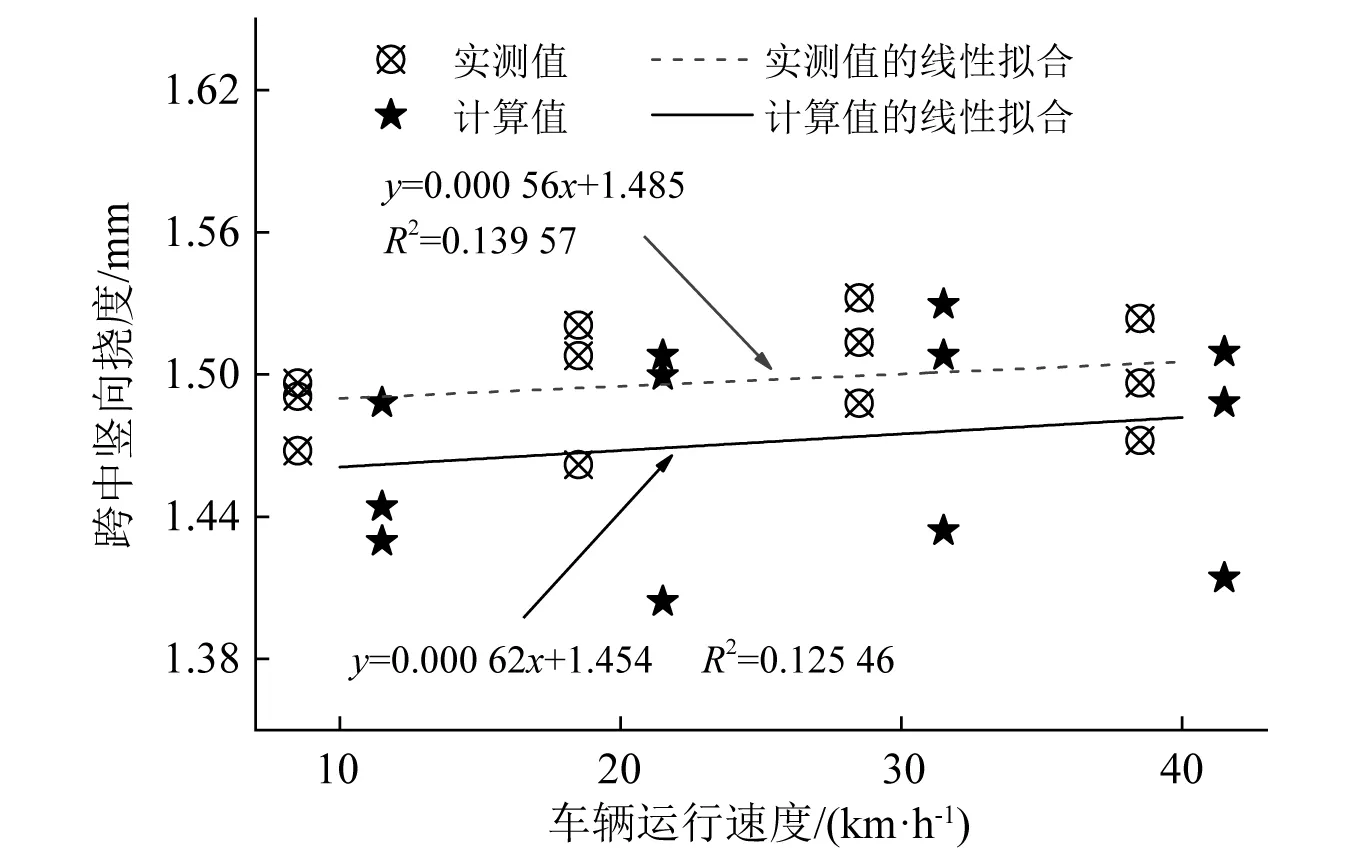
图7 不同车速下桥梁跨中竖向动挠度对比Fig.7 Comparison of vertical dynamic deflections in the middle span of bridges at different speeds

由图7可知，车辆10～40 km/h运行时，桥梁跨中竖向动挠度计算值与实测值变化趋势基本一致，计算值略小于实测值，这主要是由桥梁跨度、车辆类型等的差异而引起。需要说明的是：李小珍等对10～80 km/h速度下桥梁跨中动挠度拟合结果为y=0.000 54x+1.485，拟合度R2=0.188，与截取10～40 km/h重新拟合的结果基本一致，这说明本文用于模型验证所选取的数据是合理的。

2 中低速磁浮车辆系统动力响应分析

本节从频域方面对小半径曲线上车辆关键部件的振动特性进行分析说明。车辆20 km/h通过曲线段时车体、第一位悬浮架振动加速度功率谱密度，如图8所示。

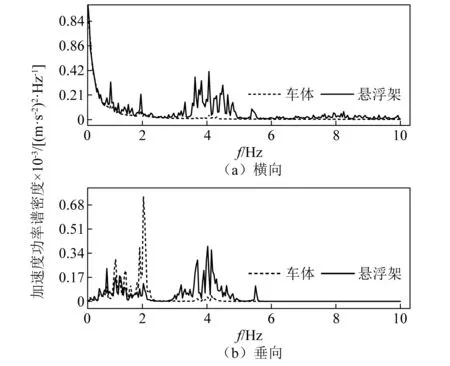
图8 车体、第一位悬浮架振动加速度功率谱密度图Fig.8 Vehicle body, first suspension vibration acc.PSD diagram

由图8可知，0～1 Hz内悬浮架横向振动加速度功率谱密度显著大于垂向，大于1 Hz时垂向振动加速度功率谱密度大于横向。车体振动加速度功率谱密度主要集中在0～2 Hz，悬浮架优势振动频率主要在0～2 Hz，3～5 Hz以及更高频段范围内。车体振动加速度优势频段范围之所以低于悬浮架，主要是由于空气弹簧的隔振作用，且频率越高隔振效果越明显，即悬浮架3～5 Hz以及更高频段范围内的振动几乎不会对车体振动产生影响。

作为与F轨直接作用的悬浮模块，进一步考虑悬浮电磁铁细观机械结构的振动特性对整车系统动力响应的影响不容忽视。车辆20 km/h运行速度下第一位悬浮架左侧电磁铁L上各线圈振动加速度功率谱密度图，如图9所示。由图9可知，悬浮电磁铁各线圈处垂向振动加速度功率谱密度显著大于横向，线圈的振动主要为40 Hz以上的高频振动。无论横向振动抑或垂向振动，电磁铁首末位置(即LF1，LR2)振动加速度功率谱密度均大于中间位置(即LF2，LR1)，且存在着明显的主频偏移现象，即首末位置振动频率主要在100 Hz附近，而中间位置振动主频在115 Hz附近。

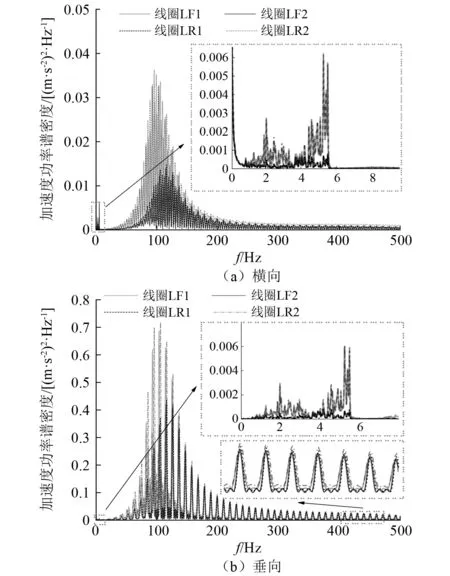
图9 悬浮电磁铁L各线圈振动加速度功率谱密度图Fig.9 Solenoid L vibration acc.PSD diagram of each coil

采用Sperling指数对车辆5～40 km/h通过该曲线段高架线路时的车辆平稳性变化进行评估，如图10所示。

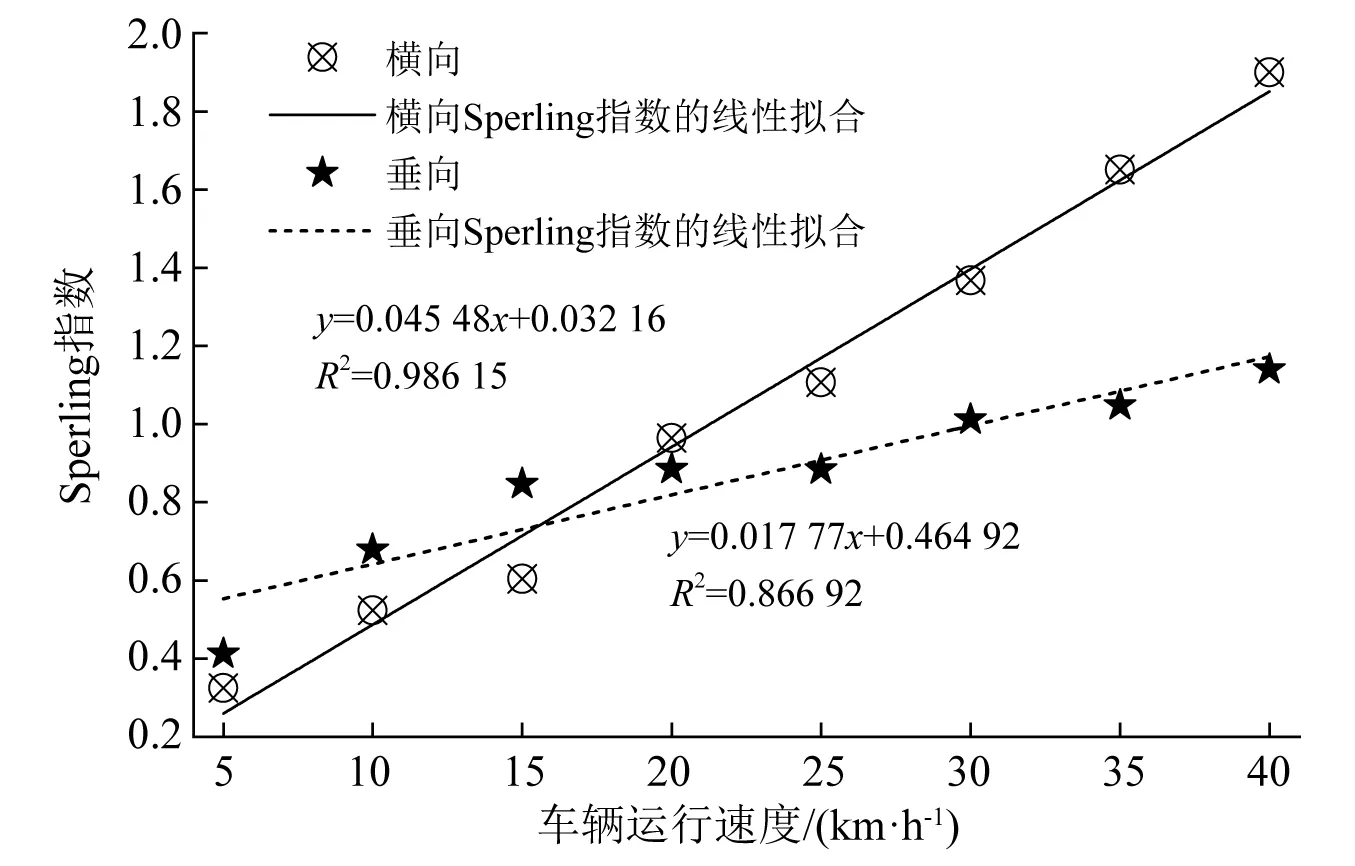
图10 车辆不同速度通过曲线线路时的平稳性指标Fig.10 The stability index of a vehicle passing through a curved line at different speeds

由图10可知，随着车辆运行速度逐渐增大，横向、垂向Sperling指数均对应增大，但横向Sperling指数变化要大于垂向，车辆速度不超过16 km/h时垂向Sperling指数大于横向，超过16 km/h时反之。横向Sperling指数之所以变化较为剧烈，这主要是由曲线线路类型和车辆结构所引起。当车辆以较高速度通过该曲线线路时，导向力由U型电磁铁复原力和迫导向机构的机械力共同提供，迫导向机构长、短T形臂中部直接与车体相连，从而对车体振动加速度产生影响，表现为车辆横向振动加速度对速度变化更为敏感，即速度引起的横向Sperling指数变化更为显著。车辆以40 km/h通过该曲线线路时，垂向Sperling指数为1.14，横向Sperling指数为1.90，均小于2.50，平稳性为优。

3 柔性高架轨道系统动力响应分析

车辆20 km/h通过该曲线段高架轨道时，桥梁横向变形及跨中竖向位移如图11所示。由图11可知，梁体水平挠度为0.39 mm，竖向挠度为1.44 mm，均在CJJ/T 262—2017《中低速磁浮交通设计规范》规定的L/2 000和L/4 600(L为梁体计算跨度)的限值之内。由竖向位移时程曲线可知，车辆在桥梁中部时梁体竖向变形最大。由横向位移时程曲线可知，车辆在缓和曲线段运行时梁体横向变形速率显著增大，圆曲线段的横向变形不及缓和曲线与圆曲线过渡处，在直缓点、缓圆点、圆缓点、缓直点过渡区上横向位移会有明显的扰动，这主要是因为不同线形之间的过渡区上线路曲率变化较为显著，从而引起导向力剧烈变化，导向力的剧烈变化引起轨道梁横向变形速率加快。

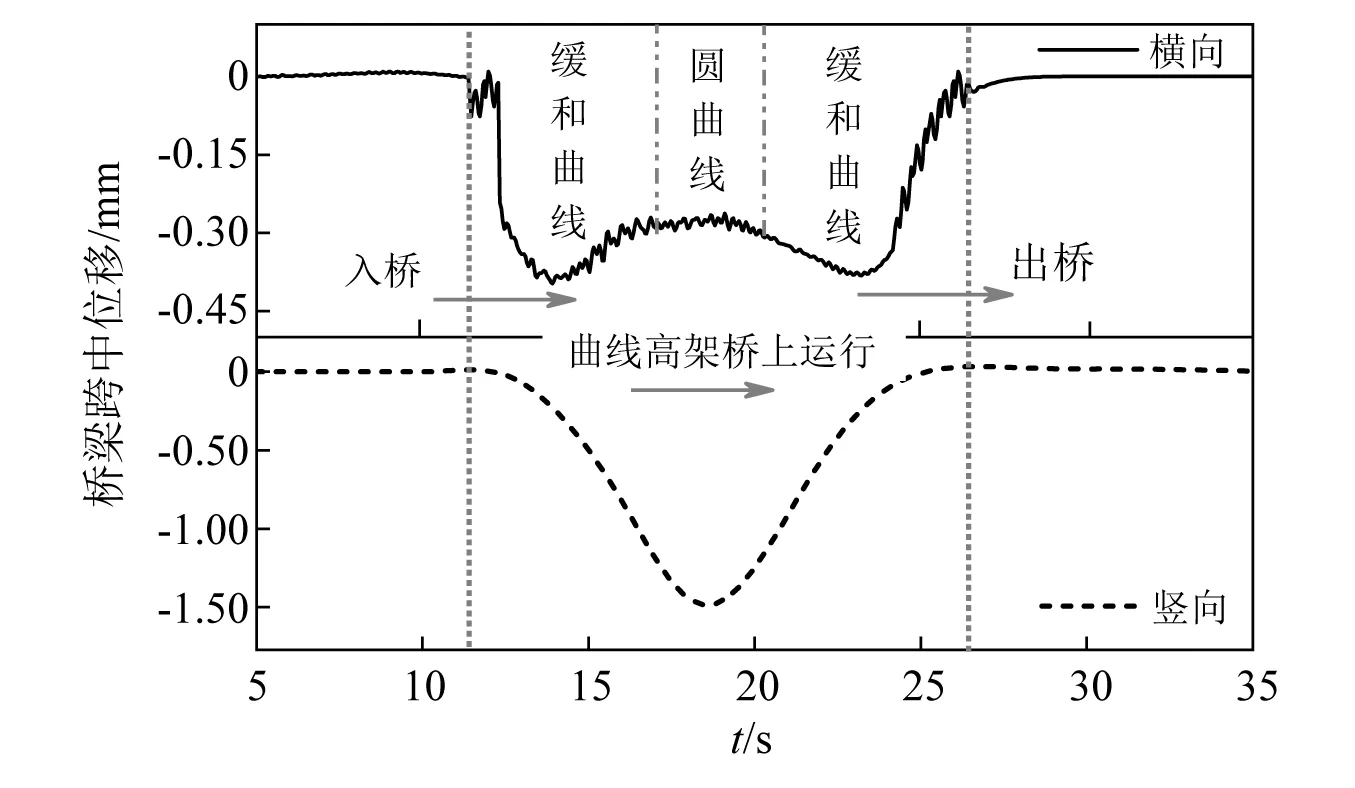
图11 曲线段高架桥梁跨中位移时程曲线Fig.11 Curved section viaduct mid-span displacement time history curve

车辆以不同速度通过该曲线线路时，梁体横向、竖向位移幅值变化，如图12所示。

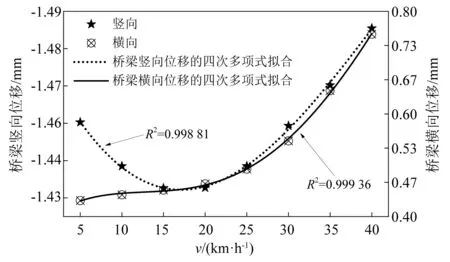
图12 不同速度下曲线段桥梁动位移Fig.12 Dynamic displacements of curved bridges at different velocities

图12中，采用四次多项式对不同速度下梁体横向、竖向位移进行了拟合，拟合函数分别为

yV=-2.40×10-11·v4-5.27×10-10·v3+2.95×
10-7·v2-9.15×10-6·v-0.002 54

(20)

yL=-5.09×10-11·v4+6.08×10-9·v3-1.82×
10-7·v2+2.21×10-6·v+5.73×10-5

(21)

式中：yV为梁体竖向位移；yL为梁体横向位移；v为车辆通过速度，v∈[5,40]。式(20)拟合度R2=0.998 81，式(21)拟合度R2=0.999 36，两者均极接近1，这表示拟合函数可较为准确的反映车辆通过速度与梁体变形的关系。

由图12可知，当车辆通过速度大于15 km/h时，随着车速增加桥梁竖向、横向位移均对应增大，且增大程度基本相同，而当车辆运行速度小于15 km/h时，随着速度增加，梁体横向位移略有增加而竖向位移不断减小。在5～40 km/h速度范围内，可近似认为速度越大梁体变形越大，这与图7一致，但就细观变化而言，由于图7拟合度较差，因此式(20)更能准确描述不同速度下梁体竖向位移变化情况。在车辆速度小于15 km/h时桥梁竖向位移随车速增大而减小，这极有可能是较低速度范围内的车轨耦合振动引起梁体竖向变形增大，而速度增大时车轨耦合振动减弱，从而梁体变形对应减小。

车速20 km/h通过该曲线轨道时，轨道结构振动加速度功率谱密度，如图13所示。桥梁-轨道系统典型自振模态如图14所示。

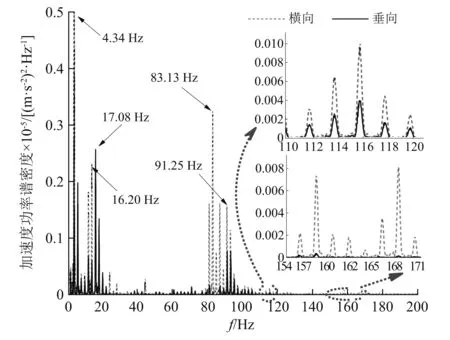
图13 高架桥梁-轨道结构振动加速度功率谱密度图Fig.13 Viaduct bridge-track structure vibration acc.PSD

图14 桥梁-轨道系统典型自振模态Fig.14 Typical vibration modes of bridge-track systems

由图13可知，该曲线段高架轨道结构振动频率主要集中在0～20 Hz和80～100 Hz内，其中0～20 Hz内垂向振动加速度功率谱密度大于横向， 80～100 Hz及更高频段范围内横向振动加速度功率谱密度显著大于垂向。0～20 Hz为轨道结构的整体振动变形频段，该频段内垂向振动加速度功率谱密度最大值对应频率为4.34 Hz，次大值对应频率为17.08 Hz，横向振动加速度功率谱密度最大值对应频率为4.34 Hz，次大值对应频率为16.20 Hz。对轨道结构进行模态分析，上述典型频段范围对应模态振型见图14。轨道结构横向和垂向振动加速度功率谱密度最大时对应频率为4.34 Hz，与图14(a)对应频率极为接近。图14(a)的模态振型为轨道结构弯扭变形，此时轨道在横向和垂向上均会发生变形且其自振频率较低，故对应振动加速度功率谱密度较大；横向振动加速度功率谱密度次大值对应频率为16.20 Hz，与图14(b)自振频率极为接近，此时对应于轨道结构的横向弯曲变形；垂向振动加速度功率谱密度次大值为17.08 Hz，与图14(c)自振频率极为接近，主要为轨道扭转和垂向弯曲变形，故以垂向振动为主，同时也会伴随有一定的横向振动。结合图13中横向和垂向功率谱密度数值，对比同为轨道弯扭变形的图14(a)和图14(c)可知，轨道弯扭变形会同时引起垂向、横向振动加速度变化，但最终决定横向或垂向振动加速度功率谱密度大小的是弯曲变形方向。

80～100 Hz为轨道结构中F轨局部变形频段，该频段内横向振动加速度功率谱密度最大值对应频率为83.13 Hz，垂向振动加速度功率谱密度最大值对应频率为91.25 Hz，与上述典型频率接近频段范围对应振型如图15所示。与83.13 Hz接近的F轨自振频率有83.001 9 Hz和83.700 0 Hz，其对应振型见图15(a)和图15(b)。图15(a)中F轨两侧发生垂向弯曲和扭转变形，中间部位为横向弯曲变形，图15(b)为F轨的横向弯曲变形。与91.25 Hz接近的F轨自振频率为91.138 2 Hz，对应振型见图15(c)。两侧以F轨横向弯曲变形为主，中间部位主要为F轨的垂向弯曲和扭转变形。

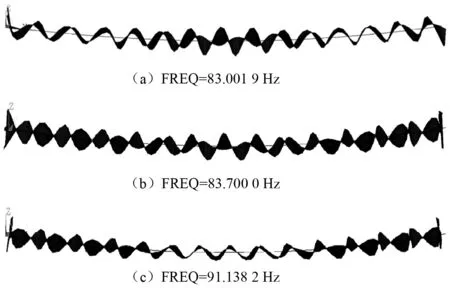
图15 F轨典型自振模态Fig.15 Typical natural modes of F rail

综上可见，在低于20 Hz的频段范围内，轨道结构弯扭变形是下部结构振动的主要原因，而轨道结构的高频振动主要是由于F轨的局部弯扭变形引起。

为进一步探究不同车辆运行速度下曲线段轨道结构振动特性，采用振动加速度有效值对其进行描述。不同速度下轨道结构垂向振动加速有效值变化，如图16所示。由图16可知，随着车辆通过速度增大，缓和曲线和圆曲线上垂向振动加速度均对应增大，但圆曲线段轨道垂向振动加速度数值大小不及缓和曲线。在同一曲线线路上，由于车辆进出缓和曲线时线路曲率变化在时空上呈轴对称而非同步变化，进一步考虑车辆迫导向机构的特殊性和轨道振动加速度的瞬时变化特性，对进出缓和曲线段独立分析。

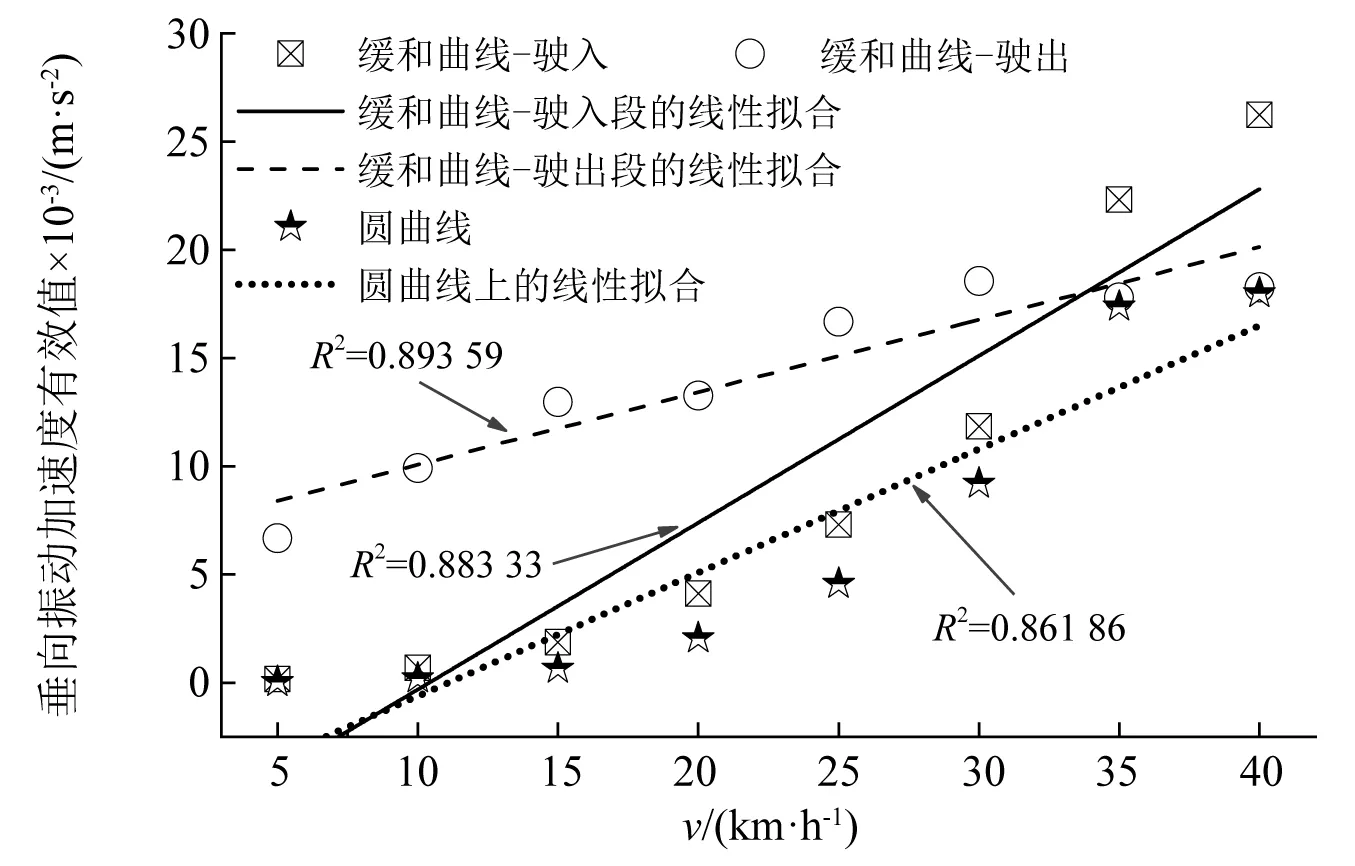
图16 不同速度下曲线段轨道垂向振动加速度有效值Fig.16 Effective value of vertical vibration acceleration of curved track at different velocities

车辆驶出缓和曲线段对应的垂向加速度大于驶入缓和曲线(见图16)，这主要是因为驶出缓和曲线时车辆是从圆曲线向直线段的过渡，圆曲线上线形变化引起的加速度变化本身极为剧烈，即相当于缓和曲线上初始振动加速度就较大，而驶入时是直线段与圆曲线之间的过渡，直线段上加速度本身较小，即相当于进入缓和曲线时初始加速度较小，故在低速时表现为驶出时垂向振动加速度大于驶入时，但驶入段是线形变化速率逐渐增大的过程，车辆速度越高时车轨作用力越显著，其引起的轨道振动也就越大，在车辆速度大于35 km/h时驶入缓和曲线时的振动加速度大于驶出时也验证了上述分析的准确性。

不同速度下轨道结构横向振动加速度有效值变化，如图17所示。由图17可知，随着车辆运行速度增大，车辆进出缓和曲线时轨道横向振动加速度均对应增大；速度不超过35 km/h时驶出段横向振动加速度大于驶入段；速度大于35 km/h时驶入段大于驶出段，这与前文图16垂向振动加速度变化一致。对不同速度下圆曲线段横向振动加速度进行线性拟合，其斜率为k=1.123×10-7，可见车辆速度对圆曲线段横向振动加速度影响极为微弱，主要是因为圆曲线上曲率恒定，车轨横向相互作用力瞬时变化较为稳定。