面结构光在机检测的叶片反光抑制技术
2022-05-30李茂月刘泽隆赵伟翔肖桂风
李茂月,刘泽隆,赵伟翔,肖桂风
(哈尔滨理工大学 机械动力工程学院,黑龙江 哈尔滨 150080)
1 引言
薄壁叶片零件是汽轮机、航空发动机的关键部件,其表面几何参数及表面质量的好坏会严重影响此类零件的工作性能或使用寿命。对加工过程中的叶片进行在机检测,可根据检测数据在线指导叶片加工,同时可避免离线测量中反复装夹易产生形变和加工效率降低的缺点[1]。结构光检测技术是近年来发展迅速的非接触式测量技术,由于其测量速度快,测量精度高,实时性强,在众多工业环境中得到广泛应用[2]。
结构光测量效果在很大程度上依赖于被测物体表面的光学反射特性。薄壁叶片在精铣削加工后,表面产生强烈的镜面反射,变得非常亮,使用传统的结构光方法测量时,大面积的耀光使相机拍摄的图像过饱和,导致条纹数据信息丢失,影响相位主值的提取精度[3],造成重建的点云出现大面积的孔洞。在商用设备市场中,著名测量系统供应商德国GOM 和瑞典Hexagon 对这种问题的解决方案是在工件表面喷涂抗反射涂层来改变其反射性质,使表面由镜面反射变为有利于检测的漫反射,但是涂层的厚度和均匀程度极容易带来测量误差[4]。
针对金属在结构光检测中产生强反光这一现象,国内外众多学者提出了不同解决方法。Zhang[5]、Song[6]、李兆杰[7]等人采用多重曝光的方式来解决金属表面反光的问题,核心原理是在不同曝光条件下获取n幅图像,然后将n幅图像进行数据融合,最终获得一幅最优效果的图像。Kofman Jonathan[8]、Lin[9]、Li[10]提出采用自适应条纹的方式,根据待测物的反光程度,通过调整投影的光栅灰度来解决高反光现像。采用多次曝光或改变投射图案强度等数据融合的方法在对场景进行初始测量时,由于场景未知,光源强度、曝光次数及其时间都有一定盲目性,且需要多次测量得到一组最优数据,影响了测量精度和效率,不适用于叶片的在机检测。
国内外学者还曾在硬件设备方面进行改善,采用特定设备以硬件进行辅助测试。Riviere[11]、Salahieh[12]、郝婧蕾[13]利用光的偏振性,使用不同偏振角度的偏振片置于相机前,来过滤进入相机的光线。但是,使用偏振片消除高反光的同时,降低了图像的信噪比,从而使测量精度随之下降,且增加偏振片使系统复杂,成本提升。
图像增强技术是对图像的某些特征,如边缘、轮廓、对比度等进行强调或锐化,以便于显示、观察或进一步分析与处理,广泛应用于生物医学图像、去雾图像及人脸识别领域中[14]。采用图像增强技术对相机所拍得条纹图像进行处理,可在去除高光的同时增强阴暗位置的亮度,得到清晰的条纹特征,从而解出相位,且不需要拍摄多组照片合成,无需额外添加其他硬件设备,具有检测效率高、成本低的优点,可满足叶片在机检测的需求。
本文针对加工场景下的叶片,采用面结构光的方法进行检测,提出基于Retinex 算法对具有反光现象的薄壁叶片条纹图像进行处理。首先,在不同曝光情况下检测薄壁叶片,根据条纹图像质量和生成点云的质量来确定最佳曝光的理想灰度,建立了光圈转动角度与图像平均灰度的相机响应曲线模型。随着外界环境的变化,通过光圈和曝光时间自适应调节曝光,使所拍图像处于理想灰度。然后,基于Retinex 图像增强算法,用改进的双边滤波代替高斯滤波对高光部分进行过滤,在提升图像质量的同时对边缘进行保护,再通过伽马变换实现灰度非线性增强,提高低灰度区域的亮度。最后,对表面光亮的薄壁叶片进行单目结构光检测实验,通过本文图像增强算法对所采集的条纹图像进行处理,求解相位主值并生成三维点云,验证了所提方法在消除金属表面高光对结构光三维测量影响的有效性。
2 结构光检测原理及金属反光特性
2.1 检测原理
采用投影相移结构光栅的测量方法,其原理是投影三频四步相移正弦结构光光栅,在投影过程中对每步光栅的每个频率进行图片拍摄,共3×4=12 幅图像。利用多个具有一定相位差的条纹图像来计算每个像素的相位值,根据相位值计算出物体的三维信息。单目结构光测量系统模型如图1所示。
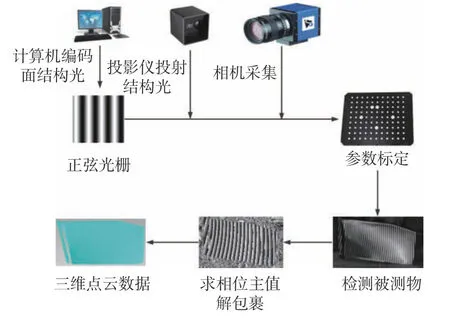
图1 单目结构光测量系统模型Fig.1 Monocular structured light measurement system model
采用标准的四步相移法计算光栅图像的相位主值[15],光强表达式为:
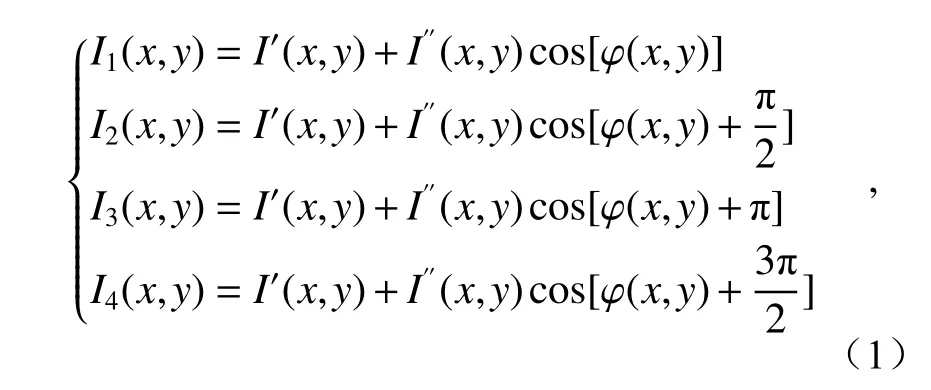
式中,Ii(x,y) 为第i幅条纹图在坐标(x,y) 处的灰度值;I'(x,y) 为图像的平均灰度;I"(x,y) 为图像的灰度调制;φ(x,y)为所求包裹初始相位。光栅图像相位主值为:得到相位主值后,根据绝对相位值、物体与CMOS 相机和投影仪的距离,可求出对应点的高度,得到三维点云。
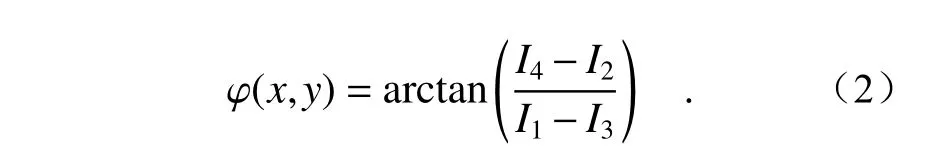
2.2 金属反光特性
金属表面的反射可分为漫反射和镜面反射,镜面反射是造成其表面有严重反光现象的主要原因。金属的镜面反射与表面粗糙度有重要关系,根据双向反射分布函数(Bidirectional Reflectance Distribution Function,BRDF) 理论[16],张颖等人[17]对铁块的镜面反射率和表面粗糙度均方根进行仿真,其镜面反射率随表面粗糙度增大而减小。王金海等[18]根据BRDF 模型,验证了在观测角与入射角相同时,镜面反射最大。薄壁叶片属于复杂曲面,与平面不同的是其表面法向量并非一致,光在其表面反射的路线不同,如图2 所示,叶片表面呈部分强反光与部分阴暗结合形态,即使改变观测角度也无法完全避免反光效果。

图2 薄壁叶片表面光照现象Fig.2 Light phenomenon on the thin-walled blade surface
3 自适应曝光调节方法
曝光是相机的重要调整参数,影响着所拍条纹图像的质量。工业相机调节曝光量有3 种方式:调节相机增益、调节镜头光圈、调节曝光时间。相机增益指的是感光器件对光线的灵敏度,调节相机增益会增加噪声,影响图像质量,一般不采用改变增益的方式调节曝光度。光圈用来控制透过镜头进入机身内感光面的光量,改变光圈影响对焦点前后的清晰范围,即景深。曝光时间指的是快门从打开到关闭的间隔时间,曝光时间越长进光量越多,但是曝光时间过长会降低相机的帧数,且工业相机所带自动曝光功能是根据比较图像当前灰度与期望灰度,逐步调节曝光时间,调节次数多,时间长。结合3 种曝光调节方式的特点以及单目结构光采集原理,本文采用恒定相机增益,通过调节光圈和曝光时间结合的方式来调整曝光量。光圈虽可改变图像的景深,但是待测叶片为相机对焦对象,景深改变不影响焦点位置的清晰度。因此,先通过光圈进行粗调,再通过曝光时间进行精调,来达到理想曝光条件。
3.1 相机响应曲线
采用工业相机拍摄图像的灰度级是28=256,灰度范围为0~255。如图3 所示,在低曝光时(见图3(a)),所拍图像亮度过暗,在高曝光时(见图3(b)),图像亮度过亮,无法得到完整的条纹信息。

图3 不同曝光下图像效果。(a) 低曝光图像;(b) 高曝光图像Fig.3 Image effects under different exposures.(a) Lowexposure image;(b) high-exposure image
图像灰度对较低和较高曝光量变化响应不敏感,对中间曝光量响应敏感,具有单调性和唯一性,其响应曲线如图4 所示。因此可根据图像的灰度值,来寻找最优的曝光量。

图4 相机响应曲线Fig.4 Camera response curve
3.2 基于灰度调整最优曝光量
采用步进电机控制光圈的大小从而改变曝光量,相机调节结构如图5 所示。

图5 相机调节结构Fig.5 Camera adjustment structure
在曝光时间不变的情况下,光圈越大,曝光量越大。与手动曝光方法相比,其提高了自动化程度和曝光准确性。步进电机采用脉冲控制,步距角ω=1.8°,兼顾电机转动精度和速度,设定细分数ν=64,电机与光圈的齿轮传动比n=1.74,则脉冲数P与光圈转动角度θ的关系式,如公式(3)所示:

即相机光圈转动1°需要输出62 个脉冲。
选用大恒工业相机MER-130-30UM-L,VST变焦镜头,光圈可转动角度为70°,待测叶片材料为铝合金,轮廓尺寸约为110 mm×50 mm。根据大恒相机使用手册推荐值,将相机增益设置为6 dB,曝光时间为30 000 μs,设置物距400 mm,将叶片作为焦点进行对焦。对焦完成后,进行最优区间的标定,考虑工件检测环境大多是暗房环境,因此在暗房条件下进行标定,固定曝光时间为30 000 μs,将光圈调零,通过电机控制,每次转动光圈5°(输出62×5=310 个脉冲),扫描叶片得到原图像、条纹图以及点云。实验过程中,光圈在转动0°~15°时,光圈通孔面积小,曝光量近乎为零,未能拍摄到叶片。选取光圈转动20°~65°的10 组数据,如图6 所示。

图6 不同曝光条件下的原图像、图像灰度值及点云图像Fig.6 Original images,image gray values and point cloud images under different exposure conditions
从点云图像看,在图像平均灰度值为74~84时,点云数据缺失较少,效果最佳。因此,确定本文材料的叶片最优曝光区间的图像灰度值为74~84。
经多次实验发现,最优曝光区间的灰度范围主要由待测物表面的反射能力决定,对于同一种金属材料来说,其反射能力相同,最优曝光区间的图像灰度值范围相差较小,具有一定的通用性。若检测对象材料发生变化,反射能力有差异,可根据基于物理渲染(Physically Based Rendering,PBR)材料反射率数据库中的金属反射系数,以铝合金的最优曝光区间的图像灰度值范围作为基准,根据金属铝与检测对象的反射率比值α,估算最优曝光区间的图像灰度值。若α>1,说明检测对象的反射能力低于铝,将铝合金的曝光灰度乘以α,以增大最优曝光的灰度;若α<1,说明检测对象的反射能力高于铝,则将铝合金的曝光灰度乘以α,以减小最优曝光的灰度。
3.3 相机曝光自适应调节
为了避免外界环境光的改变使拍摄图像的灰度不在最佳曝光区间内,在投影投射条纹之前,需对相机曝光进行自适应调节。分析实验标定数据和相机响应曲线可知,图像的平均灰度在光圈刚开始转动和光圈转动临近终点时数值响应不敏感,符合S 型曲线特性,函数峰值是光圈转动到最大位置处的图像平均灰度值Vmax。当外界环境光线变亮时,Vmax增大,当外界环境光线变暗时,Vmax减小。根据变化特性,由于光圈的转动角度为0~15°时,通光孔面积较小,光线难以进入镜头内,相机所拍图像灰度近似为零,在检测中极少使用此范围角度。建立平均灰度值V与相机光圈转动角度θ(20°<θ<70°)的相机响应函数关系式,如公式(4)所示。
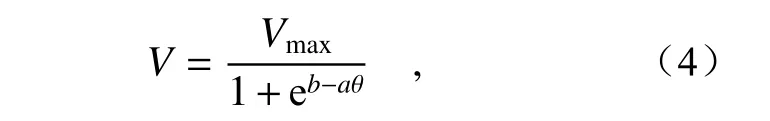
式中,a、b为S 型函数调整参数,对常规加工暗房环境下的数据采用最小二乘法拟合参数,得到参数最优解a=0.105 5,b=3.607 1,所拟合相机响应曲线如图7(彩图见期刊电子版)中实线所示,可见,随着外界环境光的改变,Vmax值发生变化,相机响应曲线也随之发生变化。图中虚线和点划线表示Vmax增大(外界环境光变亮)和Vmax减小(外界环境光变暗)时的相机响应曲线。

图7 不同环境光时的相机响应曲线Fig.7 Camera response curves under different ambient lights
根据所建立的相机响应曲线,通过调整光圈对曝光量进行自适应调节。设定最优曝光灰度值区间为74~84,图像理想灰度值为80,控制步进电机将光圈调至最大位置70°处,截取感兴趣区域,读取图像平均灰度值Vmax,得到对应的相机响应曲线,根据相机响应曲线调节光圈至图像理想灰度值80。
考虑在环境光变化时相机响应曲线中光圈转动角度与对应的灰度存在误差,若经过光圈粗调后,图像灰度未在最优曝光灰度值区间74~84 之内,采用迭代反馈的方式,通过控制曝光时间精调。设置期望灰度值为理想灰度值80,通过改变曝光时间将灰度调至理想灰度。假设光圈粗调后的图像灰度为B1,曝光时间为t1,理想灰度为B0,则下一帧的曝光时间t2的计算公式如式(5)所示。
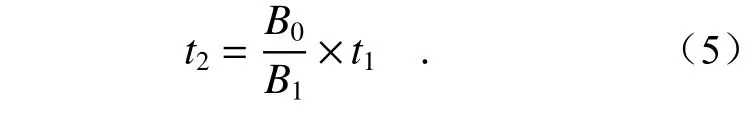
调整曝光时间至t2后,计算当前图像灰度B2,若B2在最优曝光区间内,自适应曝光调整完毕,若处在最优曝光区间外,根据公式(5)重复调整直至图像灰度处于最优曝光区间。
先通过光圈粗调使图像灰度至理想灰度值附近,再通过曝光时间精调,可减少调节曝光时间的次数,同时避免曝光时间过长引起相机帧率下降,相机曝光自适应调节流程图,如图8 所示。

图8 相机光圈自适应调节流程图Fig.8 Flow chart of camera aperture adaptive adjustment
4 基于Retinex 算法的条纹图像增强
4.1 Retinex 算法
Retinex 由视网膜(Retina)和大脑皮层(Cortex)两个词组合构成,该理论由Land 于20 世纪70 年代首次提出[19]。根据Retinex 理论,一幅图像可以看作是入射分量和反射分量的乘积,通过去除入射分量对反射分量的影响,就能达到图像增强的目的[20],其表达式如式(6)所示:

式中,I表示人眼所观察到的图像,R为反射分量,L为入射分量,(x,y)为图像中任意某点的像素。
将式(6)变换到对数(log)空间,如式(7)所示:
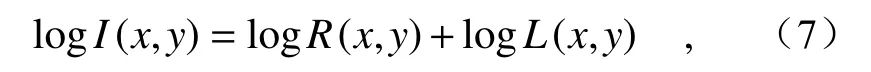
则反射分量的计算表达式如式(8)所示:
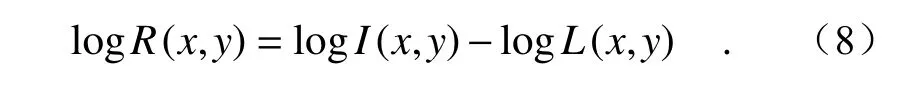
在具有强光照现象的图像中,高光属于入射光分量中的高频信息,因此采用合适的低通滤波器(中心环绕函数)将高频部分过滤,得到反射分量,再进行指数(Exp)变化恢复,就可以达到改善图像质量的目的。
经典的Retinex 算法以高斯滤波函数作为中心环绕函数,分为单尺度Retinex(Single Scale Retinex,SSR)、多尺度Retinex(Multi-Scale Retinex,MSR)算法[21]。由于高斯滤波本身所存在的缺点,导致Retinex 算法增强后的图像出现边缘模糊的问题,产生“光晕”的现象[22]。
4.2 改进的双边滤波Retinex 算法
双边滤波不仅承袭了经典高斯滤波考虑空间邻近度信息的优点,而且还考虑了灰度相似度信息。当中心像素点与其邻域像素点的灰度值之差过大时,双边滤波器将该像素点作为目标边缘区域,会令这一邻域像素点以很小的权重参与滤波,使其对中心像素点的影响很小,从而实现保护图像目标边缘的功能。因此选用双边滤波作为中心环绕函数,可有效提升图像质量并保护光栅条纹的边缘。定义(i,j) 为中心点坐标,(k,l) 为以(i,j)点为中心的邻域S 内的任意一点,则空域核定义为:

值域核定义为:

双边中心环绕函数F(i,j,k,l)则是空域核与值域核的乘积:

其中,c是空间邻域因子(即SSR 算法中的高斯环绕尺度),r是灰度相似度因子,f(i,j)是模板中心点的灰度值,f(k,l)是邻域内任一点的灰度值。
传统双边滤波在保留了过多的高频信息,且在参与滤波的邻域像素点较多时,会对边缘像素的保护产生影响。基于此,本文对其进行了改进。
(1)空域核的改进
首先,分别计算图像和滤波模板的灰度均值,分别如公式(12)、(13)所示:
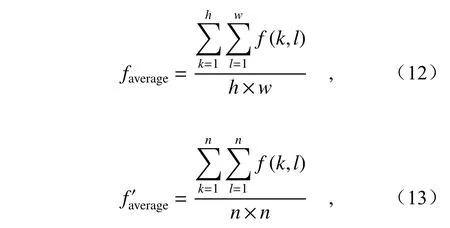
式中,h是图像高度,w是图像宽度,n是模板宽度。
空间邻域因子c越大则提取出的光照值的全局特性越好。在双边滤波模板进行逐像素卷积时,将每个模板口内的与图像的faverage进行比较,对空间邻域因子c根据初值c0进行自适应调节,若,则该位置灰度值较大,所含光照信息较多,需增大c值对光照进行过滤;反之则减小c值,改进的公式如式(14)所示:
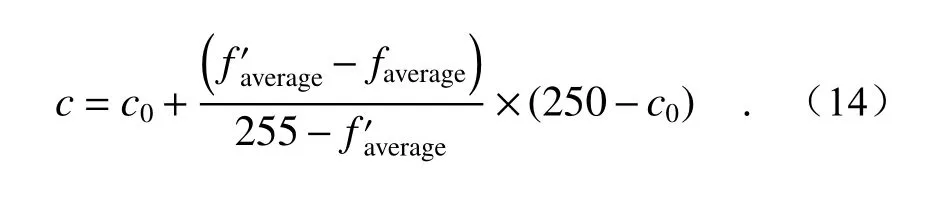
(2)值域核改进
计算滤波模板内中心点像素与其他位置像素差值Δ,设定滤波模板内中心点像素与其他位置像素差值的平均值为值域核阈值T,其公式如下:
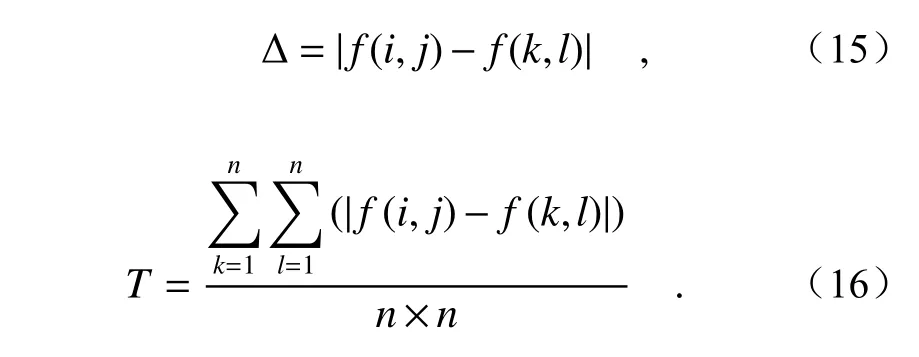
改进的灰度核函数表达式为:
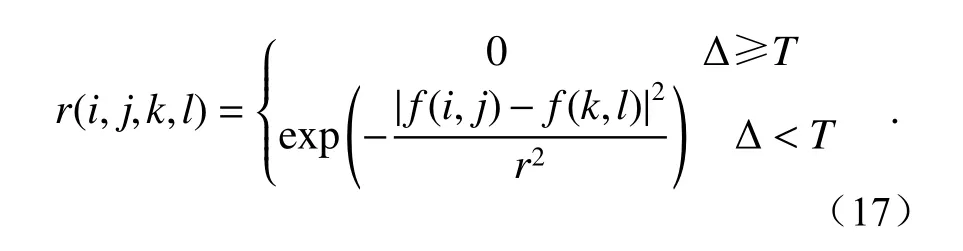
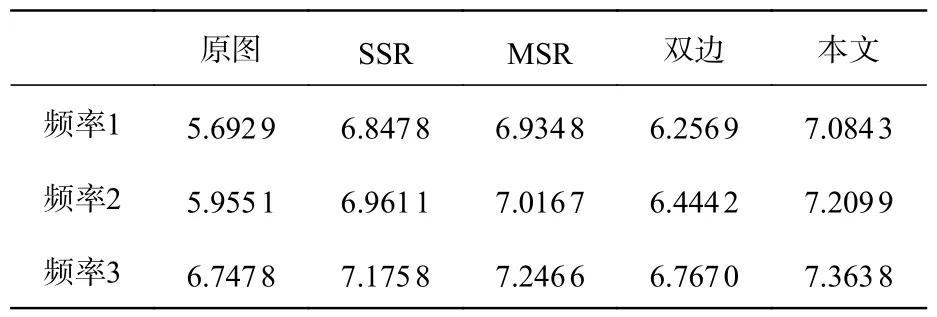
当中心像素点与其邻域某一像素点的灰度值之差Δ≥T时,认为该处为图像目标边缘部分,则令该邻域像素点的滤波权重为零,即完全不参与滤波。当Δ 伽马变换是图像处理中常用的对比度调节方法,通过非线性变换,可以使图像中较暗的区域灰度提高。本文算法在通过改进的双边滤波提取高光分量后,通过伽马变换调整对比度,以进一步增强图像细节,伽马变换公式如式(18)所示。 式中,r为原图像归一化后的灰度值,取值范围为[0,1];s为经过伽马变换后的灰度输出值;δ为灰度缩放系数,通常取1;γ为伽马因子大小,用以控制整个变换的缩放程度。 本文投射的结构光条纹为正弦条纹,对条纹图像进行对比度调节时,要保持条纹的正弦性,避免在解算相位主值时产生较大误差而影响点云的质量。结合伽马变换的特点,γ取值越接近1,其灰度改变越小,光栅正弦性保持越好。通过仿真分析得知γ分别为0.9、0.75 和0.6 时的相位主值,其误差平均值分别为0.005°、0.014°和0.027°。因此,在理想情况下保证相位主值解算在0.01°的误差范围内,伽马参数调整区间为0.8~1。算法流程如图9 所示。 图9 本文算法流程图Fig.9 Flow chart of proposed algorithm 实验采用大恒相机MER-130-30UM-L,VST变焦镜头,微型DLP 投影仪对薄壁叶片进行单目结构光检测,相机主要参数如表1 所示,实验场景和待测叶片如图10 和图11 所示。 图10 单目结构光检测实验场景Fig.10 Experimental scene of monocular structured light detection 图11 待测薄壁叶片Fig.11 Thin-walled blade to be inspected 表1 工业相机主要参数Tab.1 Main parameters of the industrial camera 通过三频四步相移求得相位主值,经解包裹后得到点云。为验证本文提出的图像增强算法,在 Intel-i7 3.25 GHz CPU,8GB RAM 的计算机上使用MATLAB R2018a 平台实现,对最佳曝光区间的12 幅条纹图像分别通过SSR、MSR、双边滤波Retinex 以及本文算法进行处理,通过Canny算子边缘检测算法检测条纹的数量、条纹图像的信息熵、相位主值图和点云偏差指标,来验证本文算法的有效性。 实验参数设置如下:窗口大小统一设置为15×15,SSR 算法中c=100,MSR 算法中c分别为15、80、250,双边滤波算法中c=100,r=0.3,本文算法中c0=100,r=0.3,γ=0.9。 每个频率选择一幅图像进行分析,图像处理效果如图12 所示。由图12 可见,对于原图左下角较暗部分,4 种算法处理后,亮度均有所增加,可得到清晰的条纹信息。对于强反光区域,SSR和MSR 算法处理后,虽然强反光有所减弱,但是产生了光晕现象,条纹边缘模糊;通过基于双边滤波的Retinex 算法处理后,条纹边缘清晰,但是对强反光位置处理较差;本文算法处理后,强反光面积大幅度减小,且条纹边缘清晰可见。 对图12 中频率3 的原图及4 种算法处理的图片通过Canny 算子边缘检测算法进行条纹边缘检测[23],验证光栅条纹图像经算法处理后清晰度是否得到改善,结果如图13 所示。通过对比可见,本文算法所检测到的条纹边缘数量最多,从侧面验证了本文算法处理效果的优越性。 图12 经不同算法处理的条纹图像Fig.12 Fringe images processed by different algorithms 图13 Canny 算子边缘检测结果Fig.13 Canny operator edge detection results 下面利用图像客观评价指标—图像信息熵,对4 种算法的条纹图像进行比较。图像信息熵是一种特征的统计形式,它反映了图像中信息量的多少,其数值越大,说明图像所含信息越多,质量越好。3 个频率的条纹图像信息熵,如表2 所示。 表2 不同方法处理前后的条纹图像信息熵Tab.2 Information entropies of fringe image by different processing methods 由表2 可见,4 种算法对3 个频率的图像处理后,图像信息熵均有所增大,其平均增长率分别为14.51%、15.68%、6.13%、18.21%,分析数据可见经本文算法处理后的图像信息熵指标涨幅最多,处理效果最优。 条纹过暗和过亮都会影响相位主值的解算,从而影响所生成点云的质量。接下来,通过相位主值图和点云来验证算法的有效性,结果如图14(彩图见期刊电子版)所示。图14 中的红色椭圆标记处是高亮位置的相位主值及其点云,可明显观察到,经过本文算法处理后得到的相位主值,其畸变面积最小。获取相位主值图中第285 行第481~600 列(图中黄线位置处)的相位主值数据,其相位主值曲线如图14 最后一行曲线图所示。该位置的中间部分产生反光,相位主值受到较大影响,而在两端未明显受到反光影响,对相位主值的影响也较小。通过对比,可见本文算法的相位主值曲线呈现较好的“锯齿”形分布,对反光及非反光区域相位主值的解算都具有较好的结果。 从图14 中的点云效果图来看,本文算法处理条纹图像解算后生成的点云,其表面数据缺失的孔洞复原,因高光产生的波纹面积最小,点云效果最优。 图14 4 种算法处理前后相位主值和点云效果对比图Fig.14 Comparison of phase principal values and point cloud effects before and after processing by four different algorithms 通过SCANTECH 品牌的PRINCE335 手持式激光三维扫描仪对叶片进行检测,获取无高光效果的点云数据进行偏差分析。由于叶榫位置形状复杂,无法一次性检测完整,因此只对叶片片体部分的点云数据进行分析,通过Geomagic Wrap平台偏差分析的效果及数据如图15(彩图见期刊电子版)所示。由偏差数据可见,经本文算法得到的点云最大偏差和平均偏差均为最小,正平均偏差由0.1064 mm降至0.0589 mm,负平均偏差由−0.1056 mm 降至−0.0590 mm,分别减少了44.6%和44.1%。 图15 点云偏差分析结果Fig.15 Point cloud deviation analysis results 通过本文所提方法再次对铝合金金属板进行结构光三维测量,尺寸为170 mm×120 mm×8 mm,其条纹图像处理结果、相位主值图及曲线、点云效果图如图16 所示。本文算法削弱了铝合金金属板条纹图像的高光信息,提升了阴暗处的对比度,相位主值解算误差小,点云表面因高光产生的波纹大幅度减少,点云质量明显提高。 图16 铝合金金属板结构光检测结果Fig.16 Structural light detection results of the aluminum alloy metal plate 综上可见,本文提出的图像增强算法有效减弱了因金属表面反光对结构光三维重构带来的影响,且效果优于传统的图像增强算法。 在对复杂曲面薄壁叶片进行检测时,其表面光亮,产生的镜面反射严重影响结构光三维重建,为解决这一问题,本文提出了一种图像增强算法来处理高光图像,并得到以下结论: (1)根据常规检测环境,标定了相机最佳曝光的灰度区间74~84,图像理想灰度值为80,建立了光圈转动角度与图像平均灰度的相机响应曲线模型,根据环境光的变化,通过光圈和曝光时间自适应调节曝光,使相机在最佳曝光区间内工作。 (2)对在最佳曝光区间采集的条纹图像进行了图像增强算法处理,基于Retinex 算法,用改进的双边滤波代替传统的高斯滤波来提取过滤高频分量,比较滤波模板内的平均灰度值和图像平均灰度值以调整空间邻域因子,并根据阈值来判断邻域点是否参与滤波,从而在有效过滤掉光照的同时保护了条纹的边缘信息。 (3)通过单目结构光检测系统对薄壁叶片进行检测实验,结果显示:与其他传统图像增强算法处理结果相比,本文算法处理的条纹图像通过Canny 算子所检测到的条纹数量最多,图像信息熵最大,平均增长率达到18.21%,相位主值计算误差最小,所生成的三维点云正负偏差降至0.058 9 mm 和−0.0 590 mm,与原点云的偏差值相比分别减少了44.6%和44.1%,表面质量得到明显改善。 本文提出的算法在面结构光三维检测时,解决金属表面因镜面反射产生的高光问题,其具有适用性,无需在工件表面喷抗反射涂层和多次测量进行数据融合,方法简单有效。但对于部分光强过强处,本文方法仍无法完全恢复其信息,所生成的点云依然存在少量波纹现象,针对该问题,后述考虑结合周边点云的曲率进行数据修复来解决。4.3 伽马变换对比度调节


5 实验与分析






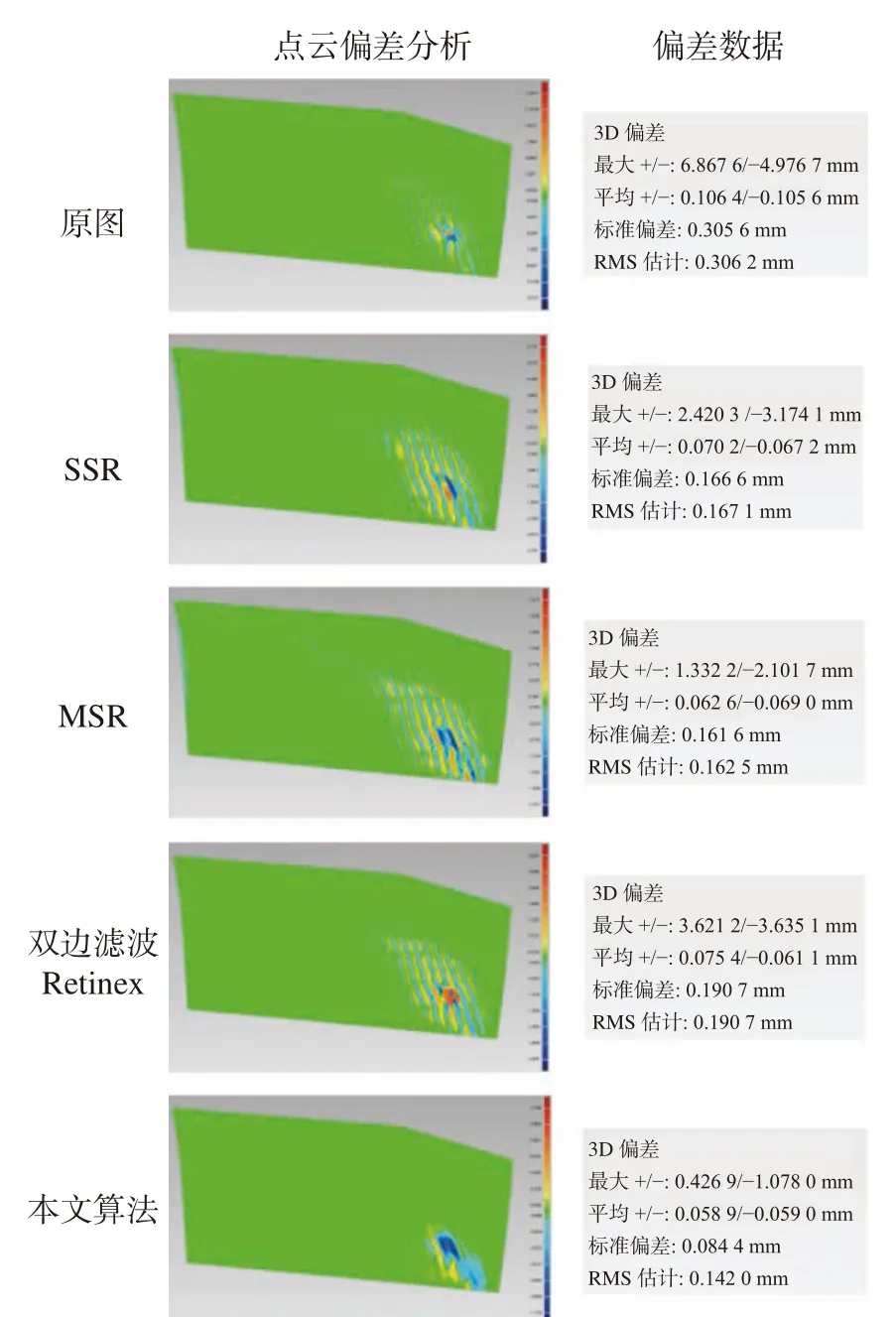

6 结论
猜你喜欢
杂志排行
中国光学的其它文章
- Structural optimization and performance testing of gold microarray electrode fabricated by DMD lithography and electrodeposition
- A study on the epitaxial structure and characteristics of high-efficiency blue silicon photodetectors
- 基于自抗扰算法的光电跟踪伺服控制方法研究
- 基于液晶光波导的电控偏振旋转器
- 基于焦面复制方法的自适应光学系统静态像差校正技术
- 航空遥感器平面反射镜系统装调方法
