基于液晶光波导的电控偏振旋转器
2022-05-28查正桃张谦述
查正桃,张谦述
(1.西华师范大学 物理与天文学院,四川 南充 637009;2.西华师范大学 电子信息工程学院,四川 南充 637009)
1 引言
偏振旋转器作为偏振调制系统中最重要的器件之一[1],可在不移动偏振器件的情况下利用波导中场分量间的能量耦合效应实现波导中横电(Transverse Electric,TE)、横 磁(Transverse Magnetic,TM)模式的相互转换[2],已被广泛应用于密集波分复用系统[3],阵列波导光栅解复用器[4]、光交叉连接[5]等研究领域。
传统偏振旋转器为无源型器件,主要通过基于非对称周期脊形波导[6-7]、弯曲波导[8-9]、混合等离子体光子晶体光纤[10]、倾斜截面波导[11]等技术实现。其中,倾斜截面波导能极大地减小偏振转换长度(Polarization Conversion Length,PCL)以及传输损耗,但对倾斜角度的尺寸要求非常严格,此外,上述其余技术均存在PCL 较大的应用局限。为此,近年来基于液晶光波导的电控偏振旋转器[5,12]逐渐引起了研究人员的兴趣,因为向列相液晶材料具有大的光学双折射[13],可满足当前偏振旋转器的超短PCL 的需要;其次,由于液晶的大电光效应导致其指向矢易被低电压驱动[14],使得液晶光波导偏振旋转器的电调谐易于实现。一般地,液晶光波导都存在取向层,使得液晶指向矢被锚定。根据Freedericksz 转变[15],当外加电压导致液晶指向矢发生偏转时,其偏转角度是沿外加电场方向渐变的,而在上述这些电控偏振旋转器的研究中并未考虑液晶指向矢的渐变特性。因此,其得出的偏振旋转效率(Polarization Conversion Efficiency,PCE)是不准确的。
为了更准确地分析基于液晶光波导的电控偏振旋转器的PCL 和PCE,本文在向列相液晶介电张量沿着一个维度渐变的条件下,首先分析了由液晶磁场耦合方程组得出的本征值方程,以便于确定PCL 与外加电压的关系;然后对液晶光波导中的电场传输方程进行横向有限差分离散,进而得到了交替方向隐式束传播法(Alternate Direction Implicit-Beam Propagation Method,ADI-BPM)迭代方程组的显式表达式,用于求解液晶光波导中的传播场,从而计算出不同外加电压下的PCE。最后,给出一个数值案例,通过求解本征模式分析了液晶指向矢的渐变特性对外加电压调控PCL的影响;进一步地,将PCL 作为波导长度进行传输场的求解,并与在液晶场致重新取向均匀(液晶分子的最大偏转角作为所有液晶分子的偏转角)的假设下得出的传播场进行比较,分析了液晶指向矢的渐变特性对电场分布以及PCE 的影响。
2 原理分析
被各向同性包层环绕的向列相液晶芯光波导如图1(a)所示,其液晶芯区的宽,厚分别为w,h。

图1 (a)液晶光波导横截面示意图;(b)液晶分子偏转示意图Fig.1 (a) Schematic diagram of the cross-section of liquid crystal optical waveguide;(b) deflection diagram of liquid crystal molecular
当不存在外加电压时,液晶层上下边界的薄聚合物(内表面摩擦方向沿x轴方向)使液晶分子沿x轴取向。当氧化铟锡(Indium Tin Oxide,ITO)电极之间施加电压后,液晶指向矢nˆ将绕z轴在xoy平面内偏转,如图1(b)所示。根据Frank-Oseen 弹性连续体理论[16]和欧拉—拉格朗日变分理论[17]可得液晶指向矢的旋转角φ (y)为:

式中,V为外加电压,k11,k33为Frank 弹性常数,为阈值电压。其中,ε0为真空中的介电常数,∆ε为液晶的介电各向异性。此外,φm为液晶分子的最大偏转角。对于这种偏转,波导坐标系xyz下液晶的介电张量为[15]

式中,

式中n∥,n⊥分别表示平行和垂直液晶光轴的主轴折射率。设z轴正方向为光传输方向,根据麦克斯韦方程可得液晶中横向磁场分量间的耦合本征方程组为[18]

式中,Hx,Hy分别表示x,y方向的本征磁场分量,β表示纵向传播常数,k0≡2π/λ0,为真空中传播常数,λ0为 真空中波长。因为介电张量 ε在y方向是渐变的,导致方程组(4)为变系数偏微分方程组,但在有限差分法中,每一个单元网格区域内的介电张量都可以被认为是均匀的[19]。因此,当对方程组(4)进行有限差分离散时,其在形式上能退化为文献[19]中的常系数偏微分方程组,则根据有限差分法的网格填充规则[20]可得特征值方程为[19]

式中,M是考虑液晶渐变介电张量的条件下由本征模场的差分系数[19]填充的稀疏算符矩阵。此外,I为与M相同尺寸的单位阵,上标T 表示转置。根据耦合模理论(Coupled Mode Theory,CMT)[21],横向各向异性光波导在半拍长位置能够实现偏振旋转,且PCL 定义为

式中,上标e,o 分别对应液晶光波导中的非寻常光波和寻常光波,下标1 表示基模。联立上述各式即可得到PCL 随外加电压变化的规律。
另一方面,对于传播场,根据麦克斯韦方程组以及Douglas–Rachford 型分离[22]可得菲涅尔近似[20]下电场的传输方程为[23]

方程(7)中,neff为参考折射率,∆z为z方向的传输步长,上标l±τ 表示当前传输位置z±τ∆z,其中τ ∈{0,1/2,1} 。此外,Γx、Γy均为方程(7)中自定义的中间变量,电场振幅和横向算符的表达式如下:
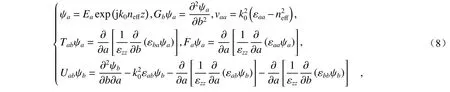
式中a,b表示x或者y,E表示电场。
尽管文献[23]中已经指出对方程(7)进行横向差分即可实现ADI-BPM 求解,但其研究对象并非为具有渐变介电张量的材料,而且也并未给出式(8)中各算符的差分表达式。因此,为了能够求解液晶光波导中的传播场,应推导出式(8)中各横向算符的显式差分表达。根据有限差分法[20],利用图2 所示的差分网格可得方程(7)所对应的ADI-BPM 迭代方程组为

图2 有限差分法中使用的网格节点示意图。(p,q) 表示中心节点,其余节点为距离其最近的8 个节点。∆x,∆y分别表示x 和y 方向上的网格间距Fig.2 Diagram of mesh nodes used in the finite difference method.(p,q) represent the central node,and the other nodes are the 8 nodes closest to the central node.∆x and ∆y are the mesh spacing in thex andy direction,respectively
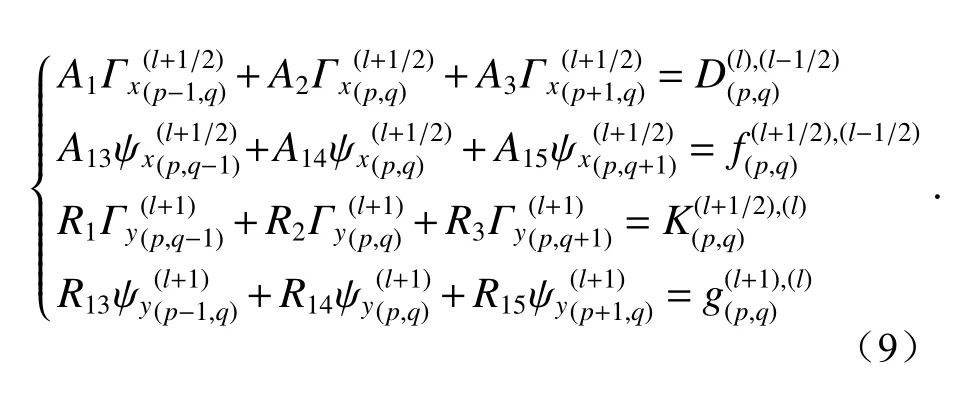
这里D,f,K,g均为含有差分系数和场强分量的表达式,在每次循环中它们都是已知量,A,R均表示与当前节点(p,q)有关的差分系数,所有这些量的具体表达式见附录。当考虑所有网格节点后,方程组(9)中每一个方程都可以改写成一个具有三对角稀疏矩阵的特征方程,在初始光场的激励下反复迭代方程(9) 即可求得传播场分布。此外,在求解中采用了透明边界条件[24]去压制波导中辐射模在计算窗口边界上引起的不必要反射。
当求得传播场后即可确定任意传输位置的PCE,根据PCE 定义[25],有

3 仿真实验
以典型的向列相液晶E7 为例,其在室温下的弹性常数为k11=11.1 pN,k33=17.1 pN以及介电各向异性 ∆ε 为13.8[26]。真空中的波长 λ0被选择为1.55 μm,根据扩展柯西方程[27]可得室温下E7 液晶的主轴折射率分别为n∥=1.697,n⊥=1.502 4。不同外加电压下介电张量关于y的曲线如图3 所示。
从图3 可以清晰地看到,当外加电压超过阈值以后,ε为y方向渐变的介电张量,而且当外加电压超过某一临界电压值后,非对角项 εxy(或 εyx)的渐变曲线不再为拱形,而是近似为M 字形。在本文当前的例子中,这一临界电压值约为阈值电压的1.26 倍,此时液晶分子的最大偏转角φm为45°。
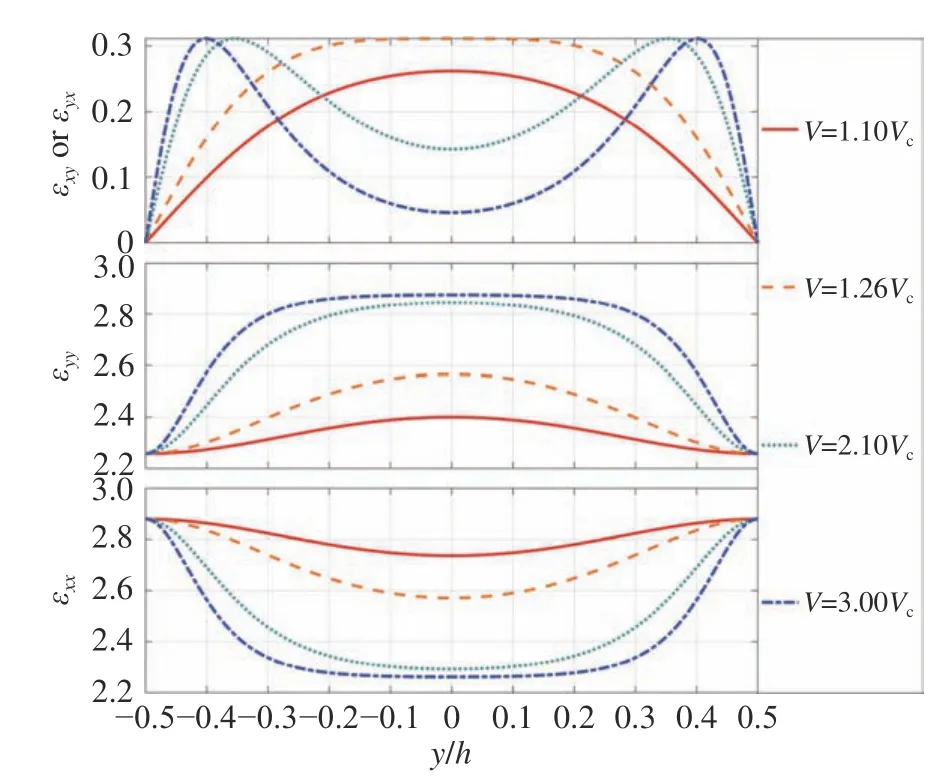
图3 不同外加电压下 εxx,εyy,εxy(或 εyx)随y 的一维渐变曲线Fig.3 One-dimensional gradual change curves of εxx,εyy,εxy (or εyx) withy at different applied voltages
此外,波导包层折射率选择为1.48,波导芯区的尺寸w,h均为5 μm,计算窗口尺寸为8 μm×8 μm,横向网格尺寸 ∆x,∆y均等于0.02 μm。图4显示了液晶场致重新取向渐变和均匀两种情况下,经特征值方程得出的PCL 与外加电压的关系曲线。应当说明的是,这两种介电张量在后文所有的图中分别对应graded 和uniform标签。

图4 PCL 分别在渐变和均匀两种介电张量下随外加电压变化的曲线Fig.4 PCL varying with applied voltage under gradient and uniform dielectric tensors,respectively
从图4 可见,通过两种液晶介电张量得出的PCL 不仅均几乎不随外加电压变化,而且它们之间的差异可以忽略。这是因为任意外加电压下所有液晶分子的光轴都始终位于xoy平面内,导致近轴光波的折射率很难随外加电压改变[28],从而使得PCL 也很难受外加电压调控。因此,可以近似认为PCL 与液晶层边界的锚定能以及外加电压均无关。这一点对于电控液晶光波导偏振旋转器的实现至关重要,因为其波导的长度通常是由PCL 决定的,而希望在改变外加电压的同时不用重新调整波导的长度,也不用考虑锚定能对其产生的影响。特别地,从图4 还可以看到这里PCL 约为4 μm,比典型的超短PCL 值[1]还小3.2 μm,这归因于液晶的大双折射率。
另一方面,尽管PCL 随外加电压的变化可以被忽略,但为了使波导终端传播场的求解结果更加精确,采用上述PCL 的平均值作为波导输出端位置,在当前的例子中约等于4.02 μm。初始激励光波选择光斑半径为2.1 μm的准-TE 高斯光(y方向电场分量可被忽略),用以模拟窄线宽激光源[29-30]。将上述特征值方程在不同电压下得出的,由非寻常光波激励的基模有效折射率的平均值作为参考折射率neff,传输步长 ∆z设为0.01 μm。考虑到图3 中非对角项的两种截然不同的渐变趋势,分别选择阈值电压的1.26 倍和2.1 倍作为外加电压值。此外,为了与之前的传输场结果进行对比,在液晶介电张量为一维渐变和均匀的两种情况下,分别对ADI-BPM 迭代方程组进行了求解。在初始位置(z=0)以及输出位置(z=处的传播场分布如图5 所示。
从图5(e)~5(f) 可见,对于均匀介电张量,当外加电压为阈值电压的1.26 倍时(φm为45°),x方向的电场分量Ex的能量几乎完全被耦合到了Ey上。然而,从图5(c)~5(d) 可见,对于一维渐变介电张量,Ex的能量却并未完全耦合到Ey上,即便此时非对角项的峰值已经增加到当前液晶材料所能达到的极限(∆ε/2);此外,从图5(g)~5(j)可见,当外加电压为2.1 倍阈值时(φm约为76°),反而是一维渐变介电张量(相比于均匀介电张量)从Ex耦合到Ey中的能量更多。为了更清晰地解释产生这一现象的原因,将这两个外加电压下X截面(yoz平面)和Y截面(xoz平面)上的传播场分布展示在图6 和图7。

图5 初始和输出位置处的电场分布。(a)~(b)初始激励;(c)~(f) 外加电压为1.26 倍阈值时输出端的传播场分布;(g)~(j) 外加电压为2.1 倍阈值时输出端的传播场分布Fig.5 Electric field distribution at initial and output positions.(a)−(b) Initial excitation;(c)−(f) propagation field distribution at the output when the applied voltage is 1.26 times the threshold;(g)−(j) propagation field distribution at the output when the applied voltage is 2.1 times the threshold
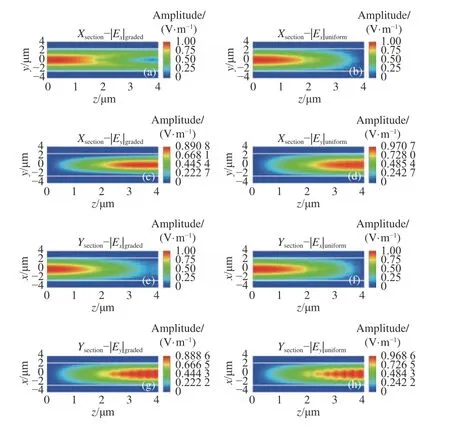
图6 外加电压为1.26 倍阈值时X 截面(a)~(d)和Y 截面(e)~(h)的传播场分布Fig.6 When the applied voltage is 1.26 times the threshold,the propagation field distribution ofX section (a)−(d) andY section (e)−(h)
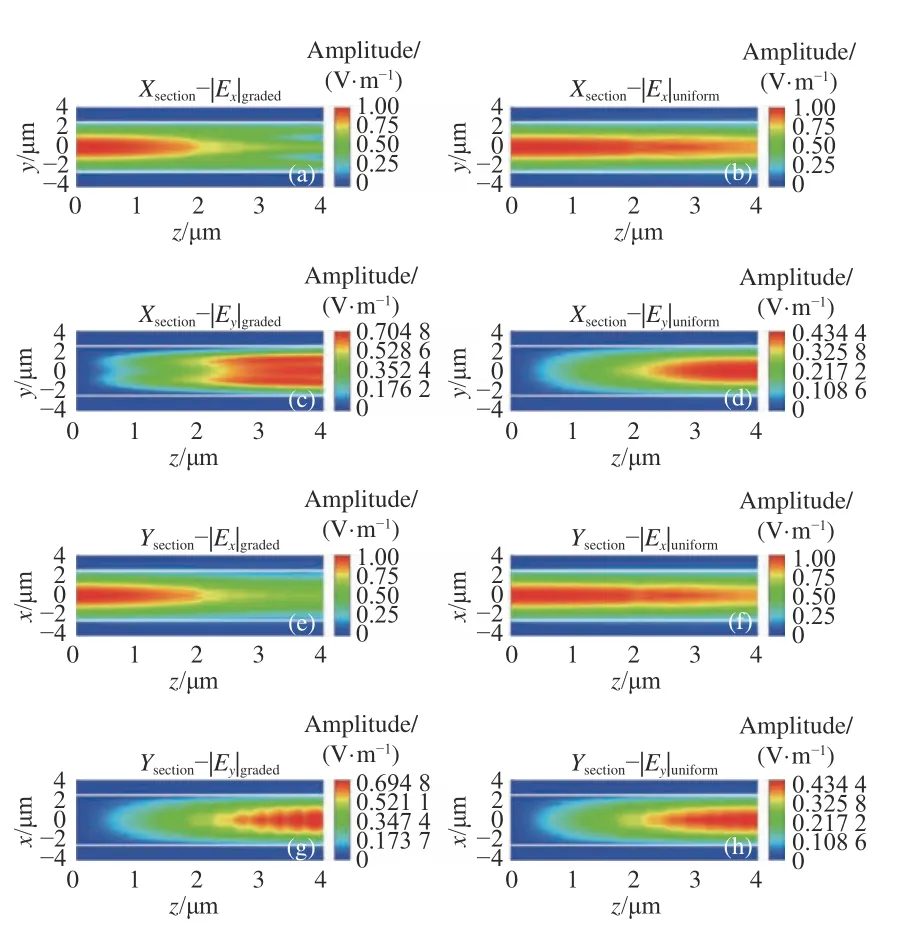
图7 外加电压为2.1 倍阈值时X 截面(a)~(d)和Y 截面(e)~(h)的传播场分布Fig.7 When the applied voltage is 2.1 times the threshold,the propagation field distribution ofX section(a)−(d) andY section (e)−(h)
从图6(e)~6(h)可见,当外加电压为1.26 倍阈值时,无论介电张量是一维渐变还是均匀的,Y截面的场强都实现了能量从Ex到Ey的几乎完全转移,这一结果与文献[5]是非常一致的,只是这里的转换是TE 到TM。然而,从图6(a)~6(d)可见,对于X截面来说,两种介电张量得出的结果存在显著的区别。与均匀介电张量下Ex的能量全部被耦合到Ey不同,一维渐变介电张量下只有波导最中心区域才实现了Ex到Ey的能量强耦合,而这一截面正是液晶分子指向矢渐变的平面。参照图3 可见,由于液晶分子是在y方向渐变的,除了波导最中心区域的部分液晶分子能具有当前液晶材料决定的最大非对角项外,其余液晶分子的非对角项都非常小,尤其是靠近液晶层上下边界的区域。根据CMT[21],非对角项越大场分量间能量耦合效应就越强,因此,在1.26 倍阈值电压下,由于液晶分子的渐变特性,在波导芯区两边(靠近上下包层)的液晶分子的耦合能力非常弱,从而导致在PCL 位置仍有很大一部分剩余的Ex,更直观的结果见图5(c)。
对于电压为2.1 倍阈值时,从图3 可见,由于此时非对角项对y的渐变趋势不再是拱形,而是M 字形,因此,其能量耦合最强的位置对称地位于波导最中心区域的两边,如图7(a)所示,更直观的结果见图5(g)。此外,从图3 还可以看到,当前电压下渐变介电张量的非对角项在液晶层的大范围内都比均匀情况下的非对角项(y=0 位置的值)更大,因此,一维渐变介电张量相较于均匀介电张量具有更强的耦合能力,如图7 (a)~7(d)所示。
为了更直观地看到液晶指向矢的渐变特性对偏振旋转器性能的影响,我们分别求解了渐变和均匀两种介电张量下,在波导输出端的PCE随外加电压变化的曲线。此外,为了与传统无源偏振旋转器的PCE 进行比较,采用通过光轴倾斜角确定的PCE 公式[31](忽略波导长度的切割误差)
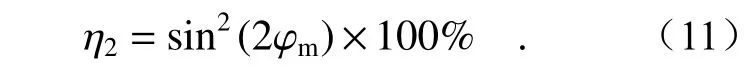
图8 展示了η1,η2随外加电压变化的关系。

图8 PCE 随外加电压变化的曲线Fig.8 PCE varying with concerning applied voltage
从图8 明显可见,在忽视锚定效应的理想情况下[12](即均匀介电张量),液晶光波导也能像无源偏振旋转器[1,31]那样可以实现接近100%的最大PCE,并且只需要几个伏特的电压就可以做到。在这里V=1.26Vc约为1.2 伏,考虑到包层具有一定的厚度,因此在实际中的电压会比这个值更大。然而,由于锚定能的作用导致液晶分子的偏转是渐变的,使得强锚定下的液晶光波导仅能实现最高约为78%的最大PCE,此时的外加电压约为1.5 倍阈值(在当前的例子中,约等于1.42伏)。此外,随着外加电压的继续增加,相较于均匀介电张量,渐变介电张量情况下的PCE 始终更大,即耦合能力更强,原因与上述分析的2.1 倍阈值电压是一致的。
进一步地,我们还可以看到渐变介电张量(相较于均匀介电张量)对应的PCE 随外加电压增加而下降得更加缓慢,而且不会持续衰减为零,即液晶光波导始终存在场分量间的耦合能力。这是因为介电张量非对角项的M 字形分布导致其始终存在两个关于波导中心对称的峰值。基于这些结果,我们可以得出液晶分子的渐变特性对其PCE 有极大的影响。
4 结论
本文在向列相液晶场致重新取向渐变的条件下,根据液晶磁场耦合方程组得出的本征值方程构建了PCL 与外加电压的对应关系,然后通过对电场传输方程进行横向有限差分离散得到了能求解液晶光波导中传播场的ADI-BPM 迭代方程组的显式表达,进而准确地分析了液晶光波导的PCL 和PCE。结果显示,液晶指向矢的渐变对PCL 的影响可以忽略,但其得出的最大PCE 相较于液晶重新取向均匀的求解结果低大约20%。因此,在基于液晶光波导的电控偏振旋转器的实际制备中,应当注意取向层的预处理(例如,采用双边对称弱锚定从而提高PCE),因为锚定能的强弱直接影响到其器件的性能。
尽管如此,基于液晶光波导的电控偏振旋转器仍然具有非常大的应用潜力,因为从我们的仿真实验中可见液晶光波导只需要4 μm 的PCL 以及几个伏特的低电压即可实现最大PCE,这是传统偏振旋转器所不具有的特性。
附录:
场量以及差分系数表达式如下:
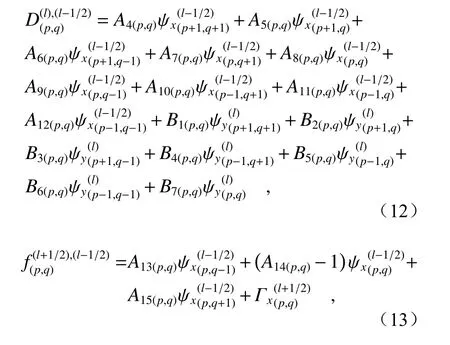

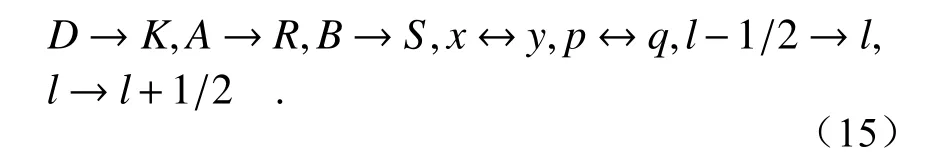

以及R1(p,q)—R15(p,q),S1(p,q)—S7(p,q)可通 过对式(14)进行如下转换得到:
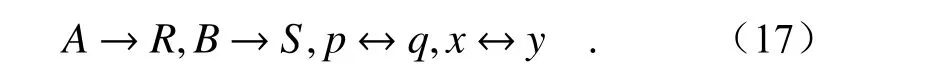
猜你喜欢
杂志排行
中国光学的其它文章
- 面结构光在机检测的叶片反光抑制技术
- Structural optimization and performance testing of gold microarray electrode fabricated by DMD lithography and electrodeposition
- A study on the epitaxial structure and characteristics of high-efficiency blue silicon photodetectors
- 基于自抗扰算法的光电跟踪伺服控制方法研究
- 基于焦面复制方法的自适应光学系统静态像差校正技术
- 航空遥感器平面反射镜系统装调方法
